Абраменко И.Г. Теория автоматического управления

141

31

20

31

3

0

aa

=Δ

;

20

31

2

aa

=Δ

;

11

aΔ=

.

Поскольку в последнем столбце определителя

n

Δ

стоят нули, за ис-

ключением

n

a

, то

1nnn

a

−

Δ= Δ

.

Пример 5.1.

САУ описывается уравнением второго порядка, характеристическое

уравнение которого имеет вид:

2

012

0ap ap a

+

+=

. Определить условие ус-

тойчивости САУ по Гурвицу.

Решение.

Составим в соответствии с (5.10) главный определитель Гурвица:

20

1

2

0

aa

a

=Δ

,

Тогда условия устойчивости системы запишутся в виде:

22121

0aaaΔ= Δ= >

;

11

0a

Δ

=>

;

0

0a >

.

Поскольку

1

0a >

, то для выполнения условия

2

0

Δ

>

, коэффициент

2

a

также должен быть больше нуля. Таким образом, для устойчивости сис-

темы второго порядка необходимо и достаточно, чтобы все коэффициенты

характеристического уравнения были положительными.

***

Пример 5.2.

САУ описывается уравнением третьего порядка, характеристическое

уравнение которого имеет вид:

32

0123

0ap ap ap a

+

++=

. Определить условие

устойчивости САУ по Гурвицу.

142

Решение.

Составим главный определитель Гурвица:

23

31

20

31

3

0

Δ==Δ a

aa

.

Тогда для устойчивой системы имеем:

332

0aΔ= Δ>

;

21203

0aa a a

Δ

=−>

;

11

0a

Δ

=>

;

0

0a >

.

Анализ приведенных неравенств показывает, что для выполнения усло-

вия положительности всех определителей Гурвица, все коэффициенты урав-

нения должны быть также положительны, но, кроме того, должно выпол-

няться неравенство:

12 03

aa aa>

.

***

Таким образом, условие положительности коэффициентов является не-

обходимым, но не достаточным условием устойчивости рассматриваемой

системы. Это утверждение остается справедливым для всех систем при по-

рядке дифференциального уравнения выше третьего (

3n >

).

Пример 5.3.

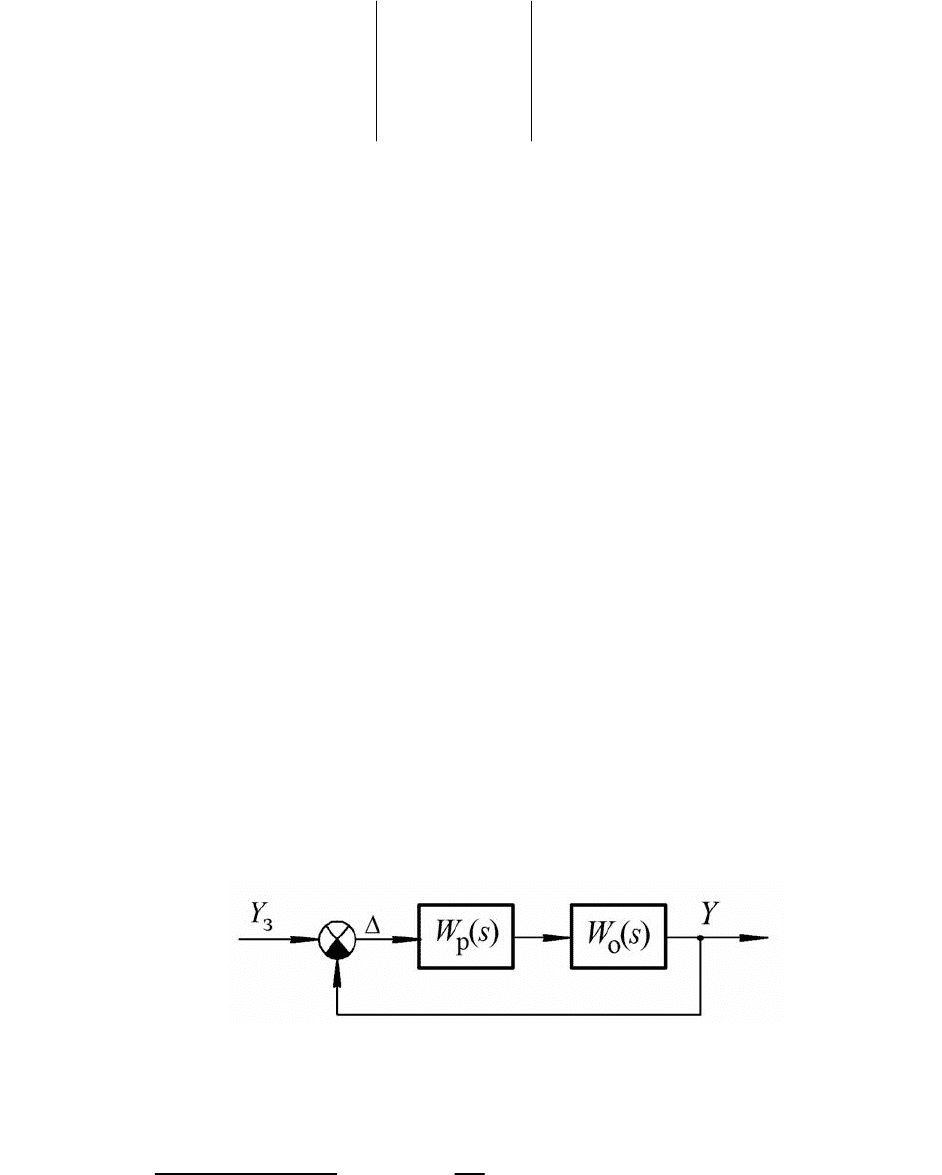
Структурная схема САУ имеет вид, представленной на рис. 5.2.

Рис. 5.2

Здесь передаточные функции элементов:

р

o

орo о

22

oo

() ; () ; 0,1 ; 0,45; 0,26

21

k

Ws Ws T c k

s

Ts T s

ξ

=====

++



Определить диапазон значений коэффициента передачи управляющего

устройства

р

k

удовлетворяющих требованиям устойчивости системы.

143

Решение.

Определим передаточную функцию замкнутой системы по каналу

з

Y →Δ

:

(

)

()

з

22

23 2

oo

23 2

22

ро

oo

р

o

oo р o

21

2

1

()

1()()

2

21

Y

Ts T s s

Ws

WsWs

Ts T s s kk

ξ

Δ

++

== =

+

+++



Тогда характеристическое уравнение системы принимает вид:

32

0123

0ap ap ap a

+

++=

,

где:

2

0 о

0, 01aT==

;

1 о

20,09aT

ξ

==

;

2

1a

=

;

3 р

0, 26ak

=

.

Согласно критерию Гурвица для устойчивой системы третьего порядка

должно выполняться неравенство

12 03

aa a a>

(см. пример 5.2).

Имеем:

12 р 03

0, 09 1 0, 01 0, 26aa k a a

=

⋅> ⋅ =

.

Откуда:

р

034,62k

<

.

* * *

5.3. Частотные критерии устойчивости

Частотные критерии устойчивости позволяют судить об устойчивости

САУ по виду их частотных характеристик. Эти критерии являются графоана-

литическими и имеют широкое распространение, так как позволяют сравни-

тельно легко исследовать устойчивость систем высоких порядков, а также

имеют простую геометрическую интерпретацию. К этой группе относятся

критерии Михайлова и Найквиста.

Перейдем к их рассмотрению

.

5.3.1.Критерий Михайлова

144

Этот критерий был сформулирован в 1938 г. русским ученым Михай-

ловым А.В. Он позволяет судить об устойчивости САУ произвольной струк-

туры на основании рассмотрения некоторой геометрической фигуры – годо-

графа Михайлова. В основу критерия Михайлова положен принцип аргумен-

та - произведение комплексных чисел имеет аргумент, равный сумме аргу-

ментов всех его сомножителей.

Приведем доказательство этого критерия.

Пусть характеристическое уравнение системы имеет вид:

1

01

() 0

nn

n

Ap ap ap a

−

=+ ++=K

, (5.11)

В соответствии с теоремой Безу характеристический полином

()

A

p

можно представить в виде:

01 2

() ( )( ) ( )

n

A

p app pp pp=−⋅− −K

, (5.12)

где

ii i

p

j

α

β

=+

- корни уравнения

() 0

A

p

=

.

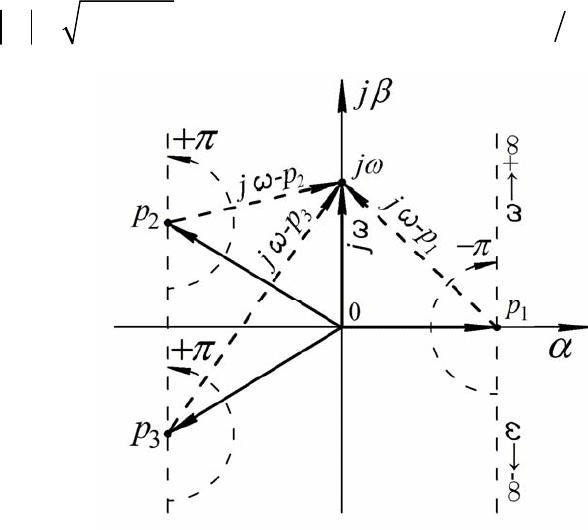
На комплексной плоскости каждый корень изображается вектором

i

p

,

проведенным из начала координат к точке

i

p

(см. рис. 5.3), модуль которого

равняется

22

iii

α

β

=+p

а аргумент -

Arg arctg( )

ii

i

β

α

=

p

.

Рис. 5.3

145

Тогда каждая скобка

()

i

pp

−

в (5.12) геометрически может быть изо-

бражена вектором, проведенным из точки с координатами

[;]

ii

α

β

к произ-

вольной точке с координатами

[Re( ); Im( )]

p

(см. рис.5.3).

Если положить

p

j

ω

=

, то получим:

01 2

() ( )( )( )

n

j ajpjp jp

ω

ωω ω

= −⋅− −=A K

)()()()(

10

1

10

ωωωω

jAAajaja

n

nn

+=+++=

−

K

, (5.13)

где

24

024

() Re ( )

nn n

Ajaaa

ωω ωω

−

==−+−A K

;

35

1135

() Im ( )

nn n

Ajaaa

ωωωωω

−

−−

==−+−A K

.

Вершины векторов

()

i

j

ω -

p

при любом конкретном значении

ω

схо-

дятся в точке

[0; ]

j

ω

.

Аргумент результирующего вектора

()

j

ω

A

, исходя из (5.13), равняет-

ся сумме аргументов векторов

()

i

j

ω -

p

, т.е.:

12

Arg ( ) Arg ( ) Arg ( ) Arg ( )

n

j

ω

=+++A

j

ω -

pj

ω -

pj

ω -

p

K

.

При изменении частоты

ω

вектор

()

j

ω

A

, изменяясь по величине и

направлению, будет описывать своим концом на комплексной плоскости не-

которую кривую, называемую кривой или годографом Михайлова.

Условимся вращение против часовой стрелки считать положительным.

Тогда при изменении

ω

от

∞

−

до

∞

+

каждый элементарный вектор в (5.13)

повернется на угол

π

, если его начало (корень

i

p

) расположено слева от

мнимой оси, и на угол

π

− , если корень расположен справа.

Предположим, что

()

A

p

имеет

m

правых корней и

)( mn −

- левых.

Тогда, при изменении

ω

от

∞

−

до

∞

+

приращение аргумента вектора

()

j

ω

A

будет:

Arg ( ) ( ) ( 2 )

j

nm m n m

ω

ωπ ππ

=

+∞

=−∞

Δ=−−=−

⏐

A

. (5.14)

Отсюда число правых корней полинома

()

A

p

может быть определено

146

в виде:

Arg ( )

2

nj

m

ω

πω

=

+∞

=−∞

−Δ

=

⏐

A

. (5.15)

Из (5.15) видно, что число правых корней системы

m

равно нулю

только в случае, если:

Arg ( )

j

n

ω

π

=

+∞

=

−∞

Δ

=

⏐

A

. (5.16)

Из уравнения (5.13) видно, что

Im ( )j

ω

A

является нечетной функцией

частоты, а

Re ( )

j

ω

A

- четной. Следовательно, годограф вектора

()

j

ω

A

состоит из двух ветвей, симметричных относительно действительной оси.

Это свойство годографа позволяет ограничиться изменением частоты только

в пределах от 0 до

∞+ .

Тогда условие (5.16) можно записать в виде:

0

Arg ( )

2

т

j

ω

π

ω

=

+∞

=

Δ=

⏐

A

. (5.17)

Условие (5.17) является необходимым, но не достаточным условием

устойчивости. Для устойчивости системы необходимо и достаточно, чтобы

среди корней характеристического уравнения не было корней, лежащих на

мнимой оси и обращающих в нуль комплексный полином

()

j

ω

A

, т.е. долж-

но выполняться еще одно условие:

()0

j

ω

≠

A

. (5.18)

Для устойчивых систем кривая Михайлова начинается при

0

=

ω

на

вещественной положительной полуоси, поскольку при

0

>a

все коэффици-

енты характеристического уравнения положительны и

0)0(

>=

n

aA

. Кроме

того, для устойчивых систем

Arg ( )

j

ω

A

с ростом частоты

ω

должен воз-

растать монотонно, т.е. вектор

()

j

ω

A

должен поворачиваться только против

часовой стрелки. Это объясняется тем, что с ростом частоты монотонно воз-

растают имеющие одинаковые (положительные) знаки, аргументы элемен-

тарных векторов

()

i

j

ω -

p

, являющиеся слагаемыми

Arg ( )

j

ω

A

.

147

Учитывая сказанное выше, критерий устойчивости Михайлова можно

сформулировать так: для того, чтобы САУ была устойчива, необходимо и

достаточно, чтобы годограф Михайлова при изменении частоты

ω

от 0

до

∞, начинался при

0=

ω

на вещественной положительной полуоси и обхо-

дил против часовой стрелки последовательно

n

квадрантов координатной

плоскости, где

n

- порядок характеристического уравнения, не обращаясь

при этом в нуль.

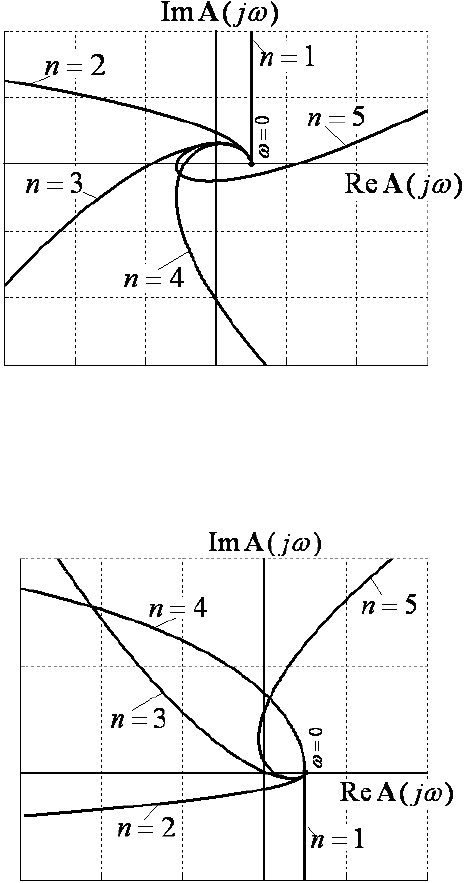
Годографы кривой Михайлова при изменении

ω

от 0 до ∞ для устой-

чивых систем при различных значениях

n

приведены на рис. 5.4.

Рис. 5.4

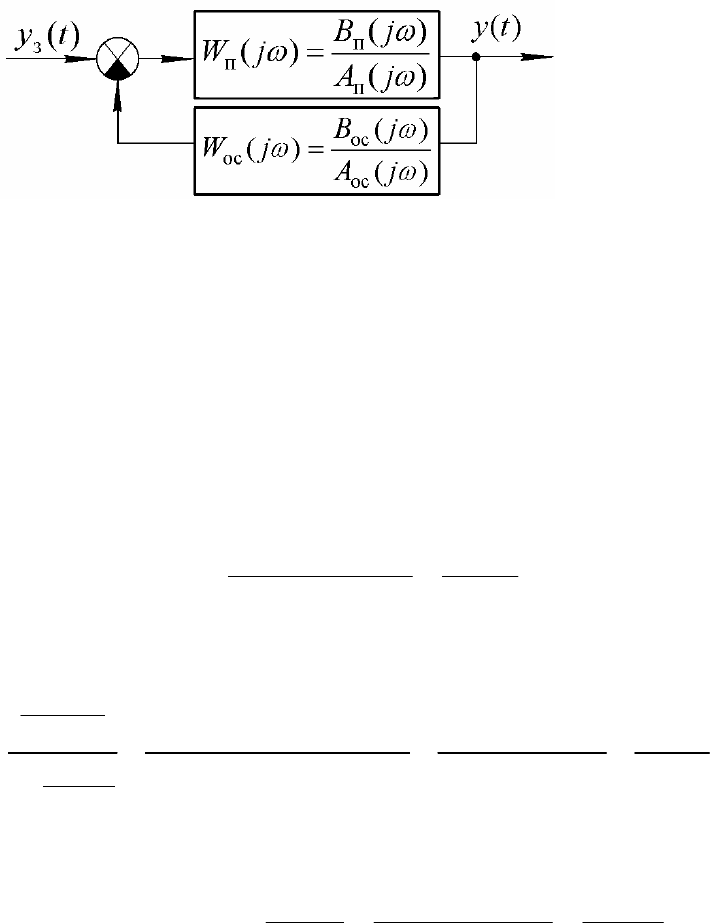
Расположение годографов на комплексной плоскости для различных

неустойчивых систем иллюстрируется рис.5.5.

Рис. 5.5

148

5.3.2. Критерий Найквиста

Этот критерий сформулирован в 1932 г. американским физиком Найк-

вистом. В отличие от ранее рассмотренных критериев, которые основаны на

использовании характеристического уравнения системы, критерий Найквиста

позволяет судить об устойчивости замкнутой системы по АФЧХ ее разомк-

нутого контура.

Рассмотрим замкнутую САУ с отрицательной обратной связью, пред-

ставленную на рис. 5.6.

Рис. 5.6

Здесь:

п

()B

j

ω

,

п

()

Aj

ω

- полиномы числителя и знаменателя частот-

ной передаточной функции прямой цепи;

ос

()B

j

ω

,

ос

()

Aj

ω

- то же, для цепи

обратной связи.

Определим частотную передаточную функцию разомкнутого контура

рк

()Wj

ω

:

пос

рк

пос

() ()

()

() () ()

BjB j

B

j

Wj

A

jA j Aj

ω

ωω

==



Определим также частотную передаточную функцию замкнутой САУ:

п

пос

пп

з

п

()

() ()

() ()()

()

()(() ()) () () ()

1

()

B

j

Bj Aj

Aj Bj Aj

Cj

Wj

Bj

A j Aj Bj Aj Bj Dj

Aj

ω

ωω

ωωω

ω

ωω ωω ω

ω

== = =

++

+



Рассмотрим вспомогательную функцию:

рк

() () () ()

()1 ()1

() () ()

B

jAjBjDj

jWj

A

jAjAj

ω

ωω ω

ωω

ω

ωω

+

Ψ=+ =+ = =



149

Из сравнения последнего соотношения с предыдущими двумя следует,

что

()

D

j

ω

- это уравнение кривой Михайлова для замкнутой системы, а

)(

ω

jA

- то же, для разомкнутой системы.

Так как в реальных системах степень

n

полинома

)(

ω

jB

не превыша-

ет степени полинома

)(

ω

jA

, то степени полиномов

()

D

j

ω

и

)(

ω

jA

оди-

наковы и равны

n

.

Выясним, как изменяется угол поворота вектора

()

j

ω

Ψ

при изменении

ω

от 0 до ∞.

Согласно правилу деления комплексных чисел этот угол определяется

выражением:

000

Arg ( ) Arg ( ) Arg ( )jDjAj

ω

ωω

ω

ωω

ωωω

=+∞ =+∞ =+∞

===

ΔΨ =Δ −Δ

⏐⏐⏐

. (5.19)

Условие устойчивости замкнутой системы согласно критерию Михай-

лова, выражается соотношением:

0

Arg ( )

2

n

Dj

ω

π

ω

=

+∞

=

Δ=

⏐

. (5.20)

В разомкнутом состоянии система может быть и неустойчивой. Поэто-

му примем, что характеристическое уравнение разомкнутой системы

() 0

A

p =

имеет

m

правых корней.

Тогда:

0

(2)

Arg ( )

2

nm

Aj

ω

π

ω

=

+∞

=

−

Δ=

⏐

. (5.21)

Подставим (5.20) и (5.21) в (5.19):

0

(2)

Arg ( )

22

nnm

j

m

ω

π

ω

π

=

+∞

=

−

ΔΨ =− =

⏐



(5.22)

Выражение (5.22) обозначает отсутствие правых корней характеристи-

ческого уравнения замкнутой системы и поэтому является необходимым и

достаточным условием устойчивости замкнутой системы.

Годограф вектора

()

j

ω

Ψ

представлен на рис.5.7, а.

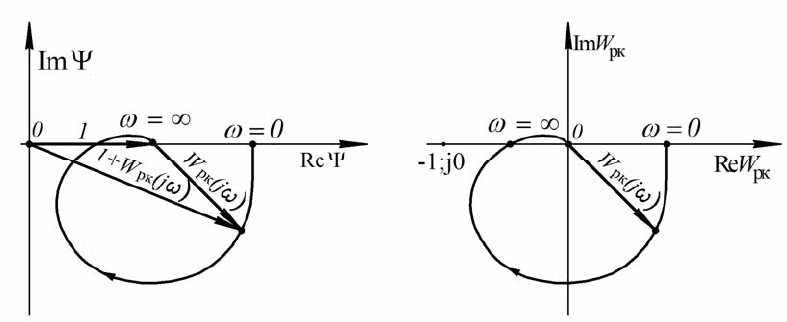
150

а) б)

Рис. 5.7

Если сместить ось ординат вправо на +1, то начало координат в новой

системе совпадет с началом вектора

рк

()W

j

ω

, а начало в старой системе

совпадет с точкой [

1−

;

0j

] (рис.5.7, б).

Тогда критерий Найквиста можно сформулировать в виде: замкнутая

система будет устойчива, если АФЧХ разомкнутой системы, имеющей

m

правых корней, при увеличении

ω

от 0 до

∞

охватит точку [

1−

;

0j

]

2/m

раз в положительном направлении.

В случае, если

0=m

, т.е. разомкнутая система устойчива, критерий

Найквиста формулируется в более простом виде: если разомкнутая система

устойчива, то для обеспечения ее устойчивости в замкнутом состоянии не-

обходимо и достаточно, чтобы АФЧХ разомкнутой системы не охватыва-

ла точку [

1−

;

0j

].

Критерию Найквиста при

0

=

m

можно дать наглядную физическую

интерпретацию. Предположим, что на входе системы действует гармониче-

ский сигнал

зз,max

() sin

y

t

y

t

ω

=

, частота которого

ω

равна частоте

π

ω

,

при которой фазовый сдвиг, создаваемый

рк

()W

j

ω

, равен

π

− .

В этом случае сигнал обратной отрицательной связи оказывается в фа-

зе с сигналом

з

()

y

t

и мгновенные значения этих сигналов суммируются.

Абраменко И.Г. Теория автоматического управления

Подождите немного. Документ загружается.