Абраменко И.Г. Теория автоматического управления
Подождите немного. Документ загружается.

101
Пример 3.4.
Определить частотные характеристики для условий примера 3.3.
Решение.
Преобразуем исходное уравнение по Лапласу при нулевых начальных
условиях:
2
(0,09 0,3 1) () 10 ()
s
sYs Xs++ =
.
Откуда можно получить выражение для передаточной функции:
2
10
()
0, 09 0, 3 1
Ws
s
s
=
+
+
.
Сделав замену
ω=
j
s
, имеем:
22
10 10
()
0, 09 0,3 1 1 0,09 0,3
Wj
jj
ω
ω
ωωω
==
−++− +
.
Получим алгебраическую форму представления
()Wj
ω
:
2
2
22
2
22
22 22
умножим и разделим на
10
()
комплексно сопр. число
10,09 0,3
10 1 0,09 0,3
1 0,09 0,3 1 0,09 0,3
10(1 0,09 ) 3
10,09 (0,3) 10,09 (0,3)
Wj
j
j
jj
j
ω
ωω
ωω
ωω ωω
ωω
ωω ωω
== =
−+
−−
=⋅=
−+ −−
−−
=+
⎡⎤ ⎡⎤
−+ −+
⎣⎦ ⎣⎦
Откуда :
2
2
22
10(1 0,09 )
()
10,09 0,09
P
ω
ω
ω
ω
−
=
⎡⎤
−+
⎣⎦
;
2
22
3
()
10,09 0,09
Q
ω
ω
ω
ω
=−
⎡⎤
−+
⎣⎦
;
{}
{
}
{}
2
22
2
22
22
22
22 22
2
22
100 (1 0,09 ) 0,09
10(1 0,09 ) 9
(ω)
1 0,09 0,09 1 0,09 0,09
10
;
1 0,09 0,09
A
ωω
ωω
ωω ωω
ωω
⎡⎤
−+
⎡⎤
−+
⎣⎦
⎣⎦
== =
⎡⎤ ⎡⎤
−+ −+
⎣⎦ ⎣⎦
=
⎡⎤
−+
⎣⎦
102
22
функция
(ω)3 3
(ω)
нечетная
(ω)
10(1 0,09 ) 10(1 0,09 )
Q
arctg arctg arctg
P
ωω
ϕ
ωω
==− ==−
−−
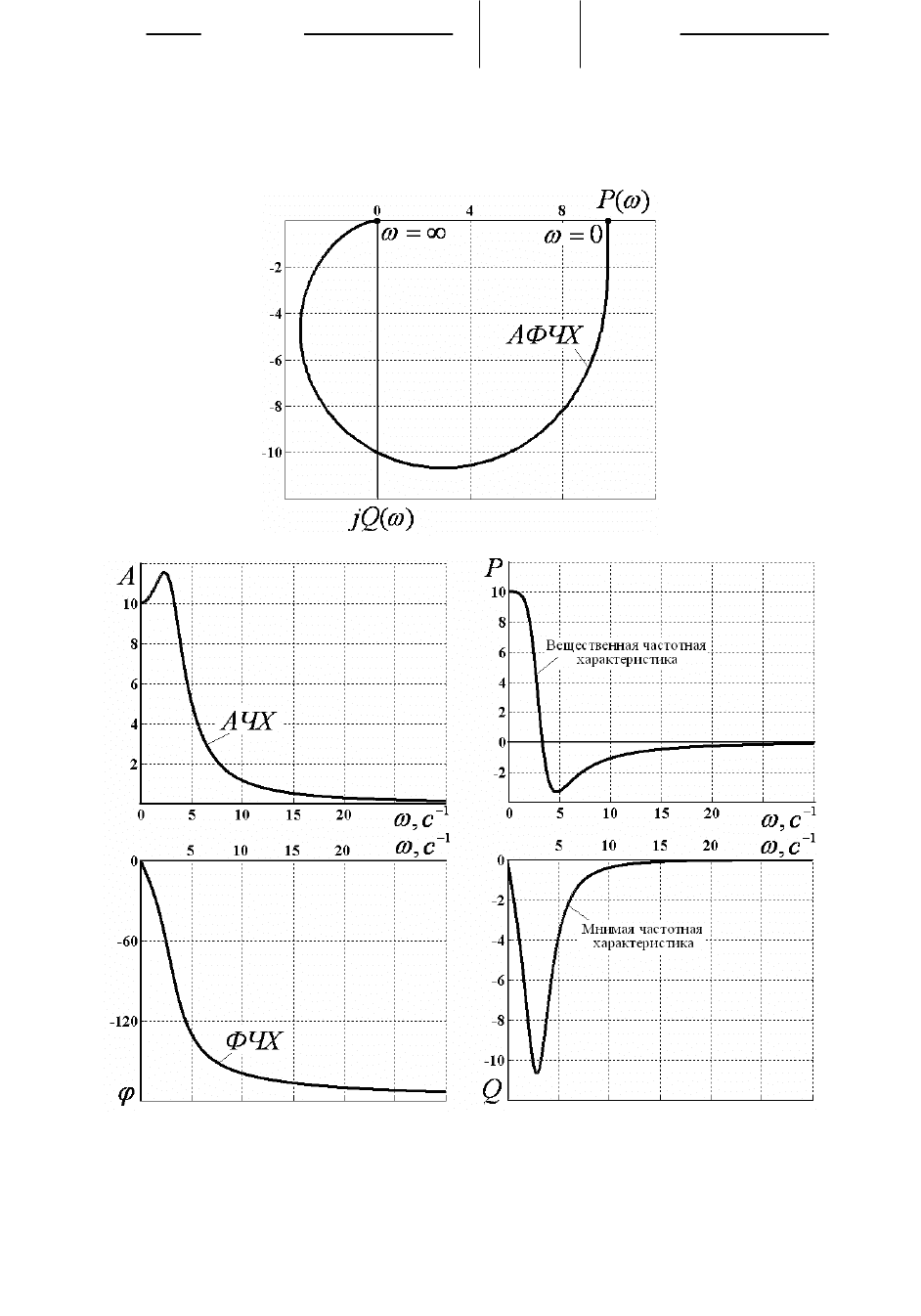
Соответствующие графики представлены на рис. 3.5.
Рис. 3.5
***
3.2.1. Логарифмические частотные характеристики
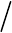
103
Исследование частотных свойств САУ значительно упрощается, если
использовать частотные характеристики, построенные в логарифмическом
масштабе. Такие характеристики называются логарифмическими частотными
характеристиками (ЛЧХ).
Выясним, что они собой представляют. Для этого прологарифмируем
)( ωjW
, выраженную в показательной форме:
lg ( ) lg ( ) ( ) lgWj A j e
ω
ωϕω
=
+
.
В полученном выражении величина
lg ( )A
ω
характеризует изменение
системой амплитуд гармонических колебаний. За единицу измерения этого
изменения принята величина
Бел1
, равная усилению сигнала по мощности в
10 раз. Так как мощность гармонического сигнала пропорциональна квадрату
его амплитуды, то при использовании этой единицы для измерения отноше-
ния амплитуд перед логарифмом
lg ( )A
ω
необходимо добавить множитель
2
. Например, если на некоторой частоте
( ) 100A
ω
=
, то это означает, что
мощности входного и выходного сигналов отличаются в
2
100
раз, т.е. на
Бел4100lg2 =
. В ТАУ используют единицу в
10
раз меньше -
дБел1
. То-
гда перед логарифмом
lg ( )A
ω
необходимо добавлять коэффициент
20
, т.е.
20lg ( )A
ω
.
График зависимости
() 20lg ()LA
ω
ω
=
, построенный в логарифмиче-
ском масштабе частот, называется логарифмической амплитудной частот-
ной характеристикой (ЛАЧХ).
За единицу измерения по оси частот принимают декаду
- интервал, на
котором частота увеличивается в
10
раз. Применяется также деление оси
ω
на октавы -
1
октава соответствует удвоению частоты. Тогда
(
)
11
1 lg 2 lg 2 0,301окт дек
ωω
===
.

104
Отметим, что для удобства пользования логарифмическим масштабом
на отметке, соответствующей значению
lg
ω
, обычно пишут само значение
ω
.
Логарифмирование оси частот позволяет сжать изображение в области
частот
1
1 c
ω
−
>
и растянуть его в области
1
1 c
ω
−
<
. При этом точке
1
0 c
ω
−
=
соответствует значение
lg
ω
=
−∞
. Поэтому при построении ЛЧХ
ось ординат проводят через некоторую произвольную точку, а не через точку
1
0 c
ω
−
=
.
График зависимости фазовой частотной функции
()
ϕ
ω
от логарифма
частоты
lg
ω
называется логарифмической фазовой частотной характери-
стикой ЛФЧХ.
Пример 3.5.
Определить логарифмические частотные характеристики для условий
примера 3.4.
Решение.
Воспользовавшись результатами, полученными в ходе решения приме-
ра 3.4, запишем:
()
() ()
2
22
22
22 22
10
() 20lg () 20lg
1 0,09 0,09
20 lg10 10 lg 1 0,09 0,09 20 10 lg 1 0,09 0,09
LA
ωω
ωω
ωω ωω
=⋅ =⋅ =
−+
⎡⎤⎡⎤
=⋅ −⋅ − + =−⋅ − +
⎢⎥⎢⎥
⎣⎦⎣⎦
Соответствующие графики представлены на рис. 3.6.
ϕ
105
Рис. 3.6
***
Использование ЛЧХ дает следующие преимущества:
1. Характеристики имеют меньшую кривизну и поэтому могут быть
приближенно заменены ломаными линиями, составленными из нескольких
прямолинейных отрезков
∗)
. Эти отрезки в большинстве случаев строятся дос-
таточно просто.
2. В логарифмической системе координат легче находить суммарные
характеристики различных соединений элементов.
3.3. Соотношения взаимосвязи характеристик САУ между собой и пере-
даточной функцией
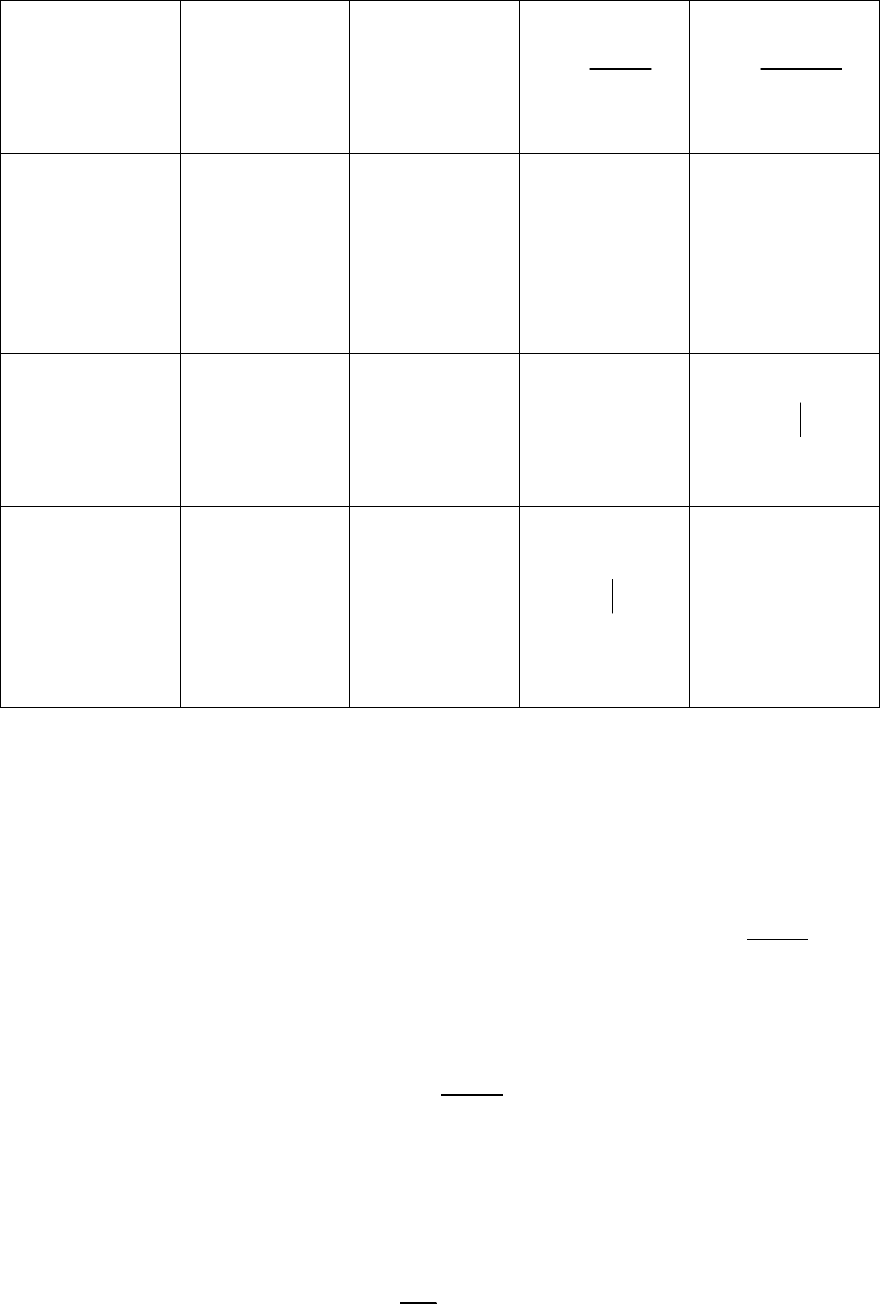
Возможные соотношеня представлены в таблице.
Характери-
стика
)(th
)(tw
)(sW
)(
ω
jW
∗)
Частоты, соответствующие точкам стыковки соседних отрезков, называются сопрягаю-
щими частотами.
106
Переходная
характери-
стика
)(th
1
∫
t
dttw
0
)(
⎭
⎬
⎫
⎩
⎨
⎧
−
s
sW
L
)(
1
⎭
⎬
⎫
⎩
⎨
⎧
ω
ω
−
j
jW
F
)(
1
Импульсная
переходная
характери-
стика
)(tw
()ht
′
1
{
}
)(
1
sWL
−
{}
)(
1
ω
−
jWF
Передаточ-
ная функция
)(sW
{}
)(thsL
{
}
)(twL
1
sj
jW
=ω
ω)(
Частотная
передаточ-
ная функция
)( ωjW
{}
)(thFjω
{
}
)(twF
ω= js
sW )(
1
Соотношения, приведенные на пересечении первых трех строк и
столбцов следуют из определения соответствующих характеристик и свойств
преобразования Лапласа. Например, из формулы
)(
)(
)(
sX
sY
sW =
при
)(1)( ttx =
получаем
)()( ssHsW
=
, где
{
}
)()( thLsH
=
.Откуда следуют соот-
ношения:
{}
sthLsW )()(
=
и
⎭
⎬
⎫
⎩
⎨
⎧
=
−
s
sW
Lth
)(
)(
1
.
Соотношения же, приведенные в последнем столбце и нижней строке
следуют из определений прямого
F
и обратного
1−
F
преобразований Фурье -
{}
1
1
() () ()
2
jt
FY
j
Y
j
ed
y
t
ω
ωωω
π
∞
−
−∞
==
∫
.

107
Контрольные вопросы
1. Какие вы знаете временные характеристики САУ?
2. Какие частотные характеристики вы знаете? Дайте их определения.
3. Как экспериментально определить частотные характеристики?
4. Как определяются частотные характеристики по передаточной функ-
ции?
5.Как строятся логарифмические частотные характеристики?
6. Зачем изучаются частотные характеристики САУ?
7. Как из передаточной функции получить выражение для АФЧХ?
8. Приведите основные формулы, связывающие АФЧХ, АЧХ и ФЧХ
между собой.
9. Какой физический смысл имеют ординаты АЧХ элемента? Как по
ним оценить условия пропускания элементом гармонического сигнала?
108
Глава 4. Типовые звенья САУ и их характеристики
Функциональные элементы, используемые в автоматических системах,
могут иметь самое различное конструктивное исполнение и самые различные
принципы действия. Однако общность математических выражений, связы-
вающих входные и выходные величины этих элементов, позволяет выделить
ограниченное число так называемых типовых алгоритмических звеньев, под
которыми понимается искусственно выделенная часть САУ, соответствую-
щая некоторому элементарному математическому
алгоритму.
Классификацию типовых звеньев удобно осуществить, рассматривая
различные частные формы дифференциального уравнения второго порядка.
)()()()()(
10210
txbtxbtyatyatya
+
′
=
+
′
+
′
′
. (4.1)
В таблице 4.1 приведены значения коэффициентов уравнения (4.1) и
названия для звеньев, реализация которых имеет физический смысл.
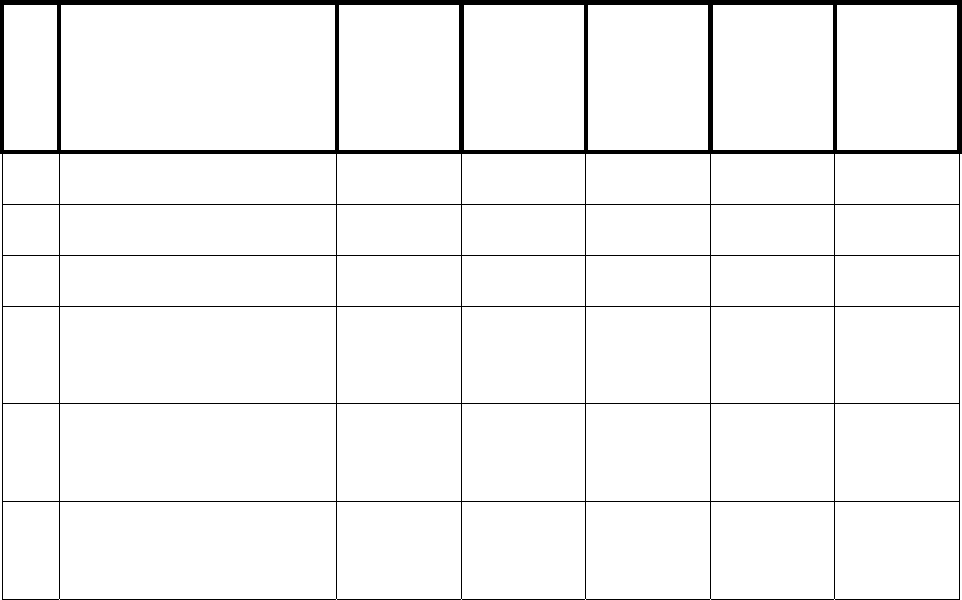
Таблица 4.1
Значения коэффициентов уравнения типовых звеньев
№
п/
п
Наименование зве-
на
0
a
1
a
2
a
0
b
1
b
1 Пропорциональное 0
0
1
0
k
2 Интегрирующее
0
1
0
0
k
3 Дифференцирующее 0
0
1
k
0
4
Апериодическое 1-го
порядка
0
T
1
0
k
5
Реальное интегри-
рующее
T
1
0
0
k
6
Реальное дифферен-
цирующее
0
T
1
k
0
109
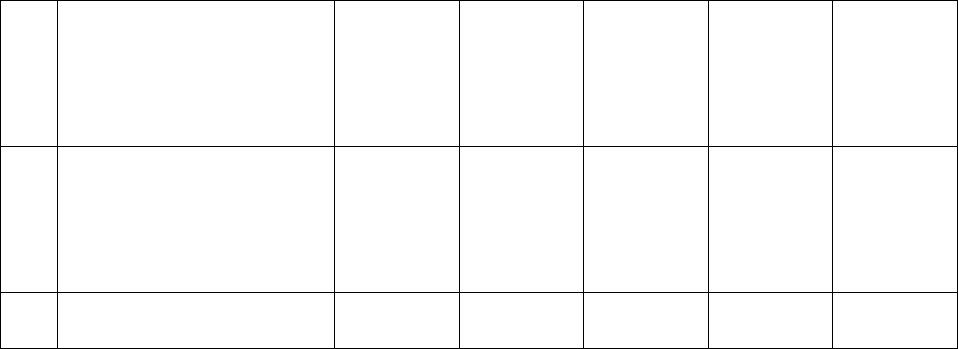
7
Изодромное (про-
порционально-
интегрирующее)
0
1
0
1
k
2
k
8
Форсирующее (про-
порционально-
дифференцирующее)
0
0
1
kT
k
9 Колебательное
2
T
T
ξ
2
1
0
k
Отметим ряд общих особенностей.
Звенья, у которых коэффициенты
0
2
≠
a
и
0
1
≠
b
, обладают однознач-
ной связью между входом и выходом в статическом режиме. К их названиям
поэтому часто добавляют слова статическое либо позиционное. К таким
звеньям относятся звенья № 1, 3, 4, 6, 8 и 9. Звенья № 2, 5, 7 называют аста-
тическими.
Звенья, у которых
0
2
≠
a
и
0
1
≠
a
или
0
0
≠
a
(№ 4, 6, 9) обладают
инерционностью (замедлением).
У звеньев № 1, 2 и 3 только два коэффициента не равны нулю. Они яв-
ляются простейшими или элементарными. Все остальные звенья могут быть
в принципе образованы из элементарных путем комбинирования.
На практике наиболее часто встречаются следующие шесть типовых
звеньев:
- пропорциональное;
- интегрирующее;
- дифференцирующее;
- апериодическое 1-го порядка;
- форсирующее
;
- колебательное.
Кроме этого к основным типовым звеньям относят также особое звено -
запаздывающее.

110
Знание свойств перечисленных звеньев существенно облегчает анализ
САУ, так как любой элемент системы и вся система в целом могут быть
представлены в виде одного или соединения нескольких типовых звеньев.
Рассмотрим свойства перечисленных звеньев в следующей последовательно-
сти:
- уравнение звена;
- передаточная функция;
- частотные характеристики – АФЧХ, ЛАЧХ, ЛФЧХ ;
- временные характеристики -
()ht
и
()wt
.
4.1. Пропорциональное звено
1. Уравнение звена:
)()( tkxty
=
,
где
k
- передаточный коэффициент, имеющий размерность
][][][ xyk =
.
В операторной форме это уравнение имеет вид:
)()( skXsY
=
.
2. Передаточная функция:
k
sX
sY
sW ==
)(
)(
)(
.
3. Частотные характеристики.
Частотная передаточная функция звена имеет вид:
()
( ) () () ()
j
Wj P jQ A ke
ϕω
ωω ωω
=
+= =
.
Поэтому
kP =ω)(
и
0)(
=
ω
Q
.
Откуда:
kA =ω)(
;
0
)(
)(
)( =
ω
ω
=ωϕ
P
Q
arctg
;
kAL lg20)(lg20)( =ω
=
ω
.
На рис.4.1 представлены соответствующие графики.
