Абраменко И.Г. Теория автоматического управления

Подождите немного. Документ загружается.

131

2. Передаточная функция:

()

−

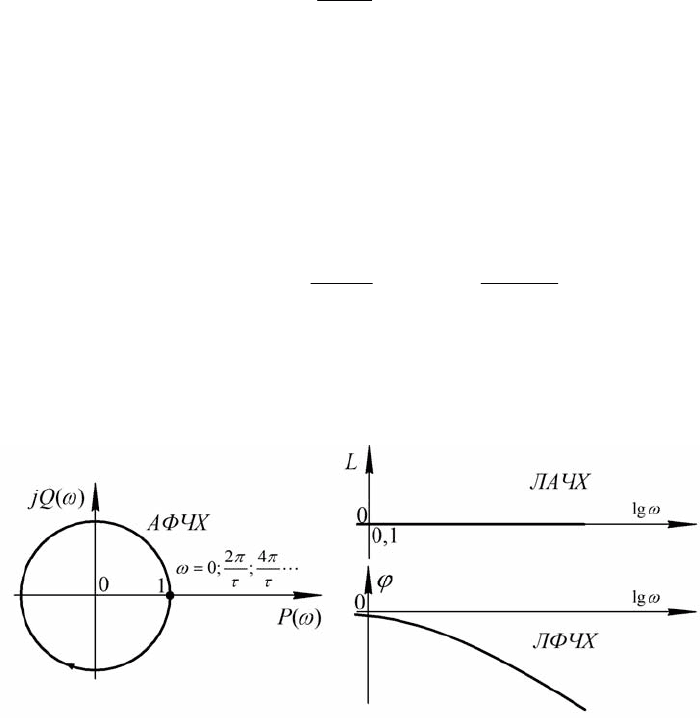
3. Частотные характеристики:

Частотная передаточная функция:

()

() ()

( ) () () () cos sin

Wj P jQ A je

ϕω

ωωω ωτωτ

=+ = = −

23 123

Откуда:

() 1A

;

() sin

( ) arctg arctg

() cos

ωτ

ωωτ

−=− =−

;

() 20l

10LA

===

На рис. 4.11 представлены соответствующие графики.

Рис.4.11

Таким образом, соотношение амплитуд входного и выходного сигналов

не зависит от частоты, а отставание по фазе выходного сигнала тем больше,

чем больше частота.

4. Временные характеристики:

- переходная характеристика

() 1( )ht t

−

;

- импульсная переходная характеристика

() () ( )wt h t t

′

=−

Вид этих характеристик представлен на рис. 4.12.

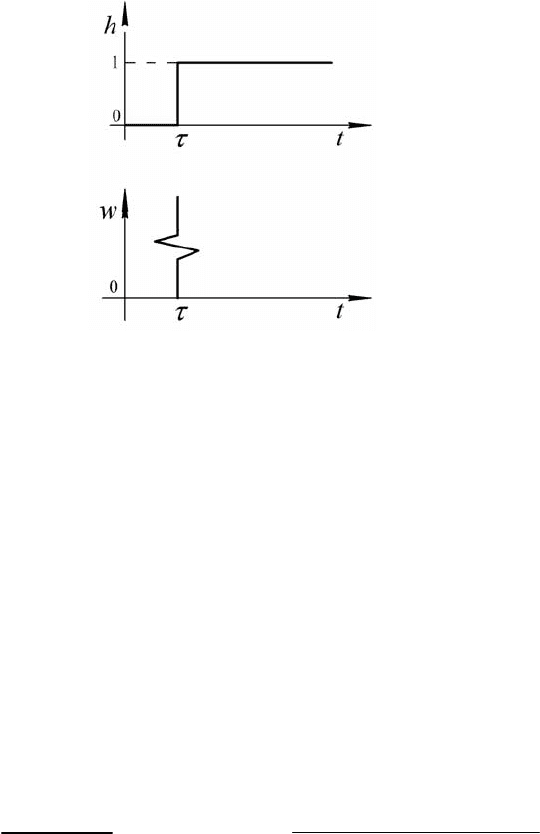
132

Рис.4.12

Следует отметить, что запаздывающее звено в большинстве случаев

ухудшает устойчивость системы, в которую входит, и делает ее трудно

управляемой. Кроме того, анализ и синтез таких систем связан с большими

трудностями.

В практических расчетах передаточную функцию запаздывающего зве-

на

)(sW

обычно приближенно заменяют дробно-рациональными функция-

ми:

10,5

()

10,5

−⋅

+⋅

или

10,5 0,83

()

10,5 0,83

ττ

−⋅+ ⋅

+⋅+ ⋅

В заключение раздела введем новое понятие – минимально-фазовое

звено. Под таким звеном будем подразумевать звено, у которого при одной и

той же частоте сдвиг фазы по модулю меньше, чем у любого другого звена,

имеющего одинаковую с ним АЧХ.

Для минимально-фазовых звеньев характерно наличие однозначной

связи между АЧХ и ФЧХ

, т.е. для него по известной АЧХ можно построить

ФЧХ.

Звено является минимально-фазовым, если все нули и полюса его пе-

редаточной функции имеют отрицательные или равные нулю вещественные

части. Таким образом, все рассмотренные выше типовые звенья, кроме за-

паздывающего, являются минимально-фазовыми.

133

Контрольные вопросы

1. Как будет изменяться выходной сигнал безинерционного звена, если

на его вход подать линейное воздействие? Постройте график

2. Как влияет безинерционное звено на амплитуду и фазу синусоидаль-

ного входного сигнала?

3. Напишите передаточную функцию инерционного звена первого по-

рядка.

4. Как проходят через инерционное звено первого порядка гармониче-

ские сигналы низкой и высокой

частоты?

5. При каком значении коэффициента демпфирования инерционное

звено второго порядка имеет апериодический переходный процесс и при ка-

ком - колебательный?

6. В чем сходство и отличие частотных свойств интегрирующих и

инерционных статических звеньев?

7. Почему дифференцирующие звенья плохо пропускают медленно ме-

няющиеся входные сигналы?

8. Постройте график выходного сигнала звена запаздывания при

подаче

на его вход линейного воздействия.

9. Напишите передаточную функцию звена запаздывания.

10. Назовите параметры колебательного звена, характеризующие его

динамические свойства.

134

Глава 5. Устойчивость САУ

5.1. Понятие, виды и общее условие устойчивости

Одной из важнейших характеристик автоматической системы управле-

ния является устойчивость. Этим понятием характеризуется работоспособ-

ность системы. Система, не обладающая устойчивостью, не способна выпол-

нять функции управления и имеет нулевую или даже отрицательную эффек-

тивность (т. е. система вредна). Неустойчивая система может привести

управляемый объект в аварийное состояние. Поэтому проблема устойчивости

систем является одной из центральных в теории автоматического управле-

ния.

Устойчивость автоматической системы - это свойство системы воз-

вращаться в исходное состояние равновесия после прекращения воз-

действия, выведшего систему из этого состояния.

Неустойчивость автоматических систем управления возникает, как

правило, из-за очень сильного действия обратной связи. Причиной динамиче-

ской неустойчивости обычно является значительная инерционность элемен-

тов замкнутого контура, из-за которой в режиме колебаний системы сигнал

обратной связи значительно отстает от входного сигнала и оказывается с ним

в фазе. Это означает, что связь, выполненная конструктивно как отрицатель-

ная, проявляется как положительная.

Рассмотрим математическую сущность устойчивости и неустой-

чивости. Согласно данному выше физическому определению устойчивость

зависит только от характера свободного движения системы. Свободное дви-

жение линейной или линеаризованной системы описывается однородным

дифференциальным уравнением:

() ( 1)

() () () 0

ay t ay t ayt

−

++ =K

, (5.1)

где

() ()yt y t=

- свободная составляющая управляемой величины системы.

135

Вынужденная составляющая выходной величины, зависящая от вида

внешнего воздействия и правой части дифференциального уравнения, на ус-

тойчивость системы не влияет.

Система является устойчивой, если свободная составляющая

()yt

пе-

реходного процесса с течением времени стремится к нулю, т. е. если

lim ( ) 0

→∞

. (5.2)

Очевидно, что при этом выходная величина системы будет стремиться

к вынужденной составляющей, определяемой внешним воздействием и пра-

вой частью уравнения (5.1). Устойчивость в смысле условия (5.2) принято

называть асимптотической.

Если свободная составляющая неограниченно возрастает, т. е. если

lim ( )

→∞

∞

. (5.3)

то система неустойчива.

Наконец, если свободная составляющая не стремится ни к нулю, ни к

бесконечности, то система находится на границе устойчивости.

Найдем общее условие, при котором система, описываемая уравнением

(5.1), устойчива. Решение уравнения (5.1) равно сумме

() ()

ii i

yt Cyt Ce

∑∑

, (5.4)

где

- постоянные, зависящие от начальных условий;

- корни характе-

ристического уравнения

ap ap a

−

++=K

. (5.5)

Корни характеристического уравнения могут быть действительными

(

), мнимыми (

) и комплексными (

ii i

). При этом

комплексные корни всегда попарно сопряжены между собой: если есть ко-

рень с положительной мнимой частью, то обязательно существует корень с

такой же по модулю, но отрицательной мнимой частью.

136

Составляющая (5.4) при t →∞

стремится к нулю лишь в том случае, ес-

ли каждое слагаемое вида

C e →

. Характер последней функции зави-

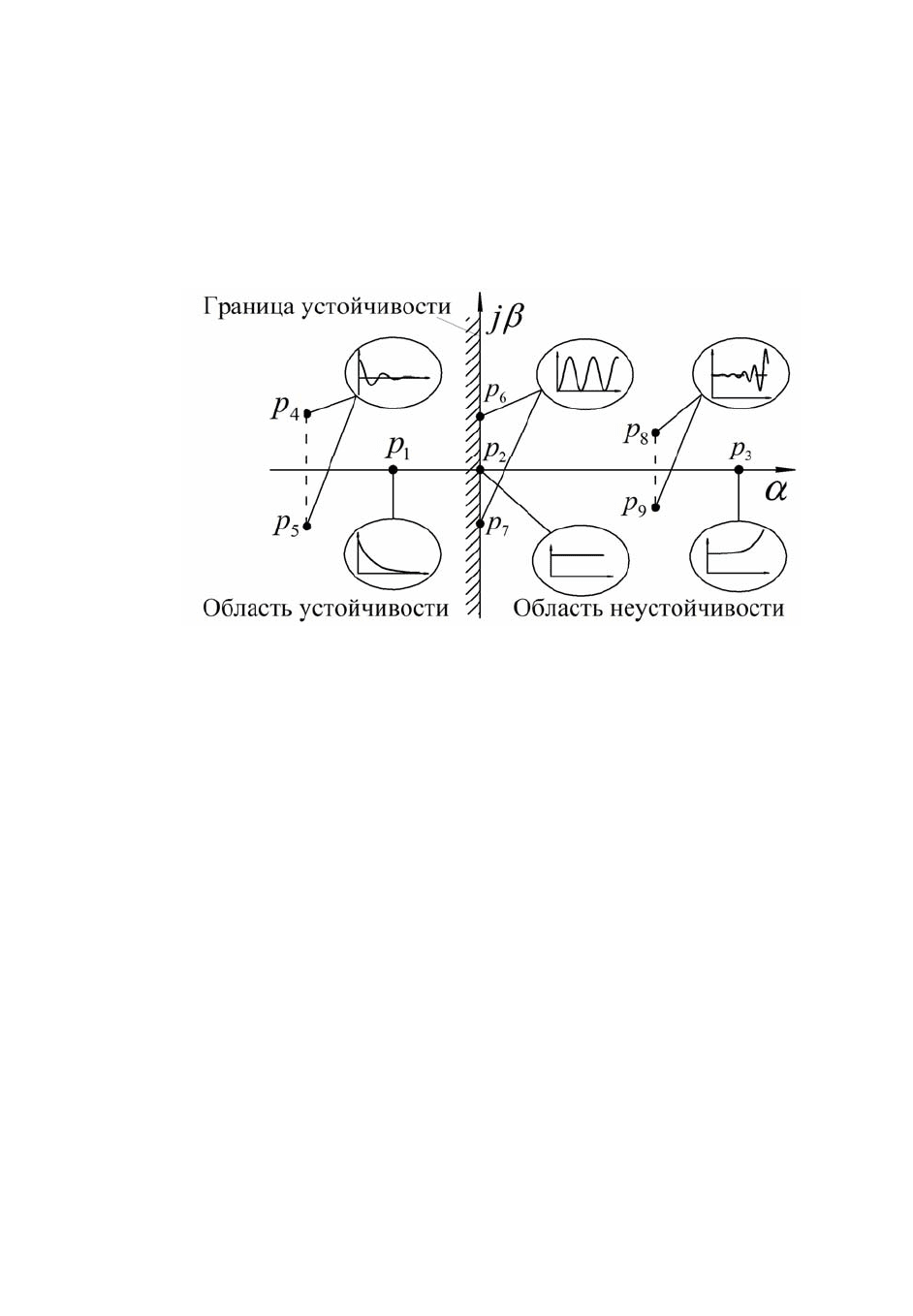
сит от вида корня. Рассмотрим все возможные случаи расположения корней

на комплексной плоскости (рис. 5.1) и соответствующие им функ-

ции

с,

()

yt Ce=

, которые показаны внутри элипсов.

Рис. 5.1. Влияние корней характеристического уравнения системы на

составляющие ее свободного движения

1. Каждому действительному корню

в решении (5.4) соответ-

ствует слагаемое вида:

с,

()

yt Ce

(5.6)

Если

(корень

), то функция (5.6) при t →∞

стремится к нулю.

Если

(корень

), то функция (5.6) неограниченно возрастает. Если

(корень

), то эта функция остается постоянной.

2. Каждой паре сопряженных комплексных корней

,1ii i i

=±

решении (5.4) соответствуют два слагаемых, которые могут быть объединены

в одно слагаемое:

с,, 1

() sin( )

ii i i i

ytA t

. (5.7)

137

Функция (5.7) представляет собой синусоиду с частотой

и ам-

плитудой, изменяющейся во времени по экспоненте. Если действительная

часть двух комплексных корней

(см. рис. 5.1, корни

), то колеба-

тельная составляющая (5.7) будет затухать. Если

(корни

), то

амплитуда колебаний будет неограниченно возрастать. Наконец, если

(корни

) т. е. если оба сопряженных корня - мнимые, то

с,

()

представляет собой незатухающую синусоиду с частотой

. Если среди

корней характеристического уравнения (5.5) имеются

равных между собой

корней

, то в решении (5.4) вместо

слагаемых вида

C e

появится

одна составляющая:

()

01 2 1

CCtCt Ct e

−

++ + +K

. (5.8)

Учитывая, что функция вида

−

при любом

убывает быстрее, чем

возрастают слагаемые вида

, можно доказать, что и в случае кратности

корней решение (5.4) будет стремиться к нулю лишь при отрицательности

действительной части кратных корней

На основании проведенного анализа можно сформулировать общее ус-

ловие устойчивости: для устойчивости линейной автоматической системы

управления необходимо и достаточно, чтобы действительные части всех

корней характеристического уравнения системы были отрицательными.

При этом действительные корни рассматриваются как частный случай

комплексных корней, у которых мнимая часть равна нулю. Если хотя бы

один корень имеет положительную действительную часть, то система будет

неустойчивой.

Устойчивость системы зависит только от вида корней характе-

ристического уравнения и не зависит от характера внешних воздействий на

систему. Устойчивость есть внутреннее свойство системы, присущее ей вне

зависимости от внешних условий.

138

Используя геометрическое представление корней (5.5) на комплексной

плоскости (см. рис. 5.1) в виде векторов или точек, можно дать вторую фор-

мулировку общего условия устойчивости (эквивалентную основной): для ус-

тойчивости линейной системы необходимо и достаточно, чтобы все корни

характеристического уравнения находились в левой полуплоскости.

Если хотя бы один корень находится в правой полуплоскости, то сис-

тема будет неустойчивой.

Мнимая ось

является границей устойчивости в плоскости корней.

Если характеристическое уравнение имеет одну пару чисто мнимых корней

,1ii i

=±

, а все остальные корни находятся в левой полуплоскости, то в

системе устанавливаются незатухающие гармонические колебания с круго-

вой частотой

. В этом случае говорят, что система находится на коле-

бательной границе устойчивости.

Точка

на мнимой оси соответствует так называемому нулевому

корню. Если уравнение имеет один нулевой корень, то система находится на

апериодической границе устойчивости. Если таких корня два, то система не-

устойчива.

Применяя сформулированное выше условие для оценки устойчивости

реальных систем, не следует забывать, что линейные уравнения типа (5.1),

как правило, получаются в результате упрощений и линеаризации исходных

нелинейных уравнений. Возникает вопрос: в какой мере оценка устойчивости

по линеаризованному уравнению будет справедлива для реальной системы,

не окажут ли существенное влияние на результат анализа отброшенные при

линеаризации члены разложения? Ответ на него был дан русским ма-

тематиком А. М. Ляпуновым в 1892 г. в работе «Общая задача об устойчиво-

сти движения». Он сформулировал и доказал следующую теорему: если ха-

рактеристическое уравнение линеаризованной системы имеет хотя бы один

нулевой корень или одну пару мнимых корней, то судить об устойчивости

реальной системы по линеаризованному уравнению нельзя. Отброшенные

139

при линеаризации малые члены могут сделать систему устойчивой или неус-

тойчивой, и поэтому устойчивость реальной системы необходимо оценивать

по исходному нелинейному уравнению.

Таким образом, для суждения об устойчивости линейной системы дос-

таточно определить лишь знаки действительных частей корней характери-

стического уравнения.

В теории автоматического управления разработан ряд правил, с помо-

щью которых можно судить о знаках корней, не решая характеристическое

уравнение и не находя числовые значения самих корней. Эти правила назы-

ваются критериями устойчивости. Простейшим критерием устойчивости

является условие положительности коэффициентов характеристического

уравнения. Положительность коэффициентов уравнения (5.5) является необ-

ходимым (но не достаточным) условием устойчивости системы. Это означа-

ет, что если все коэффициенты положительны, то система может быть устой-

чивой или неустойчивой. Но если хотя бы один коэффициент сравнения от-

рицателен или равен нулю, то система неустойчива. Критерии устойчивости

могут быть алгебраическими и частотными. Алгебраические критерии уста-

навливают необходимые и достаточные условия отрицательности корней в

форме ограничений, накладываемых на определенные комбинации коэффи-

циентов характеристического уравнения. Частотные критерии определяют

связь между устойчивостью системы и формой частотных характеристик

системы.

При анализе устойчивости систем управления обычно решают одну

или несколько задач: 1) оценивают, устойчива или нет система при заданных

параметрах; 2) определяют допустимый по условию устойчивости диапазон

изменения некоторых незаданных параметров системы; 3) выясняют, может

ли система при заданной структуре быть в принципе устойчивой.

5.2. Алгебраические критерии устойчивости

140

Наиболее распространенным в инженерной практике является крите-

рий Гурвица. Этот был сформулирован и доказан в 1895 г. немецким матема-

тиком А. Гурвицем, который разработал свой критерий, решая чисто матема-

тическую задачу - задачу исследования устойчивости решений линейного

дифференциального уравнения. Применительно к задачам теории управления

критерий Гурвица можно сформулировать так: система, описываемая ха-

рактеристическим уравнением

=+++

−

apapa K

. (5.9)

устойчива, если при

0a >

положительны все определители Гурвица

,,,

ΔΔ ΔK

Эти определители составляются по следующим правилам:

1) по главной диагонали выписывают все коэффициенты от

до

порядке возрастания индекса;

2) дополняют столбцы определителя вверх от диагона-

ли коэффициентами с последовательно возрастающими, а вниз – с последо-

вательно убывающими индексами;

3) на место коэффициентов, индексы которых больше n и меньше 0,

ставят нули.

В соответствии с этими правилами, определитель Гурвица

-го по-

рядка для уравнения (5.9) имеет вид:

135

024

000

aaa

Δ=



MMMMM

(5.10)

Определители Гурвица более низкого порядка являются диагональны-

ми минорами

. Например, при n = 3