Абраменко И.Г. Теория автоматического управления
Подождите немного. Документ загружается.

61
Линеаризовав функцию
в
() [ () ]F Ф t
f
it w
=
−⋅
в окрестностях базовых
значений переменных,
в,0
i
и
0
Ф
, в соответствии с (2.20) получим:
вв
() ()Ф tk it
Δ
=⋅Δ
, (2.32)
где
в
в
0
Ф
kw
i
∂
=⋅
∂
.
Запишем в отклонениях уравнение (2.10):
в
вввв
()
() ()
dit
ut R it L
dt
Δ
Δ=⋅Δ+
. (2.33)
Преобразовав (2.29) и (2.30) по Лапласу и исключив промежуточную
переменную
в
()IsΔ
, получим:
в
в
вв
() ()
k
Ф sUs
RLs
Δ= Δ
+
. (2.34)
С учетом (2.26), (2.31) и (2.34) система уравнений ДПТ с независимым
возбуждением (2.15) принимает вид:
2
эм м
12 э
д,u двд,Мэ с
в
() () ()
(1 )
() () (1 ) ()
1
TT s s T s s s
kk Ts
kUs Usk TsMs
Ts
⋅ ⋅ΔΩ + ⋅ ⋅ΔΩ + ΔΩ =
++
=Δ + Δ − +Δ
+
, (2.35)
где:
э
TLR
ΣΣ
=
- электромагнитная постоянная времени;
()
2
м 0
TJRcФ
ΣΣ
=⋅
- электромеханическая постоянная времени;
ввв
TLR=
- постоянная времени обмотки возбуждения;
д,u 0
1( )kcФ=⋅
- передаточный коэффициент двигателя по напряже-
нию;
д,М
kR
Σ
=
- передаточный коэффициент двигателя по моменту;
1 в 0 в 0
()kk RФ
ω
=⋅ ⋅
;
2
1 вяц,0 в 0
()kki R RсФ
Σ
=⋅ ⋅ ⋅⋅
.
***
2.2. Математическое описание САУ в переменных состояния

62
Метод переменных состояния основан на понятии состояния.
Состояние системы в момент времени
0
t
- такой минимальный набор
сведений о ней, которого вместе со входной функцией
()ut
, заданной для ин-
тервала времени
0 k
ttt≤≤
, достаточно для однозначного определения
выходной функции
)(ty
для
0 k
ttt
≤
≤
при любом
0k
tt≥
.
Состояния системы можно охарактеризовать совокупностью некото-
рых переменных
12
(), (), , ()
n
x
txt xtK
, знание начальных значений которых
12
(0), (0), , (0)
n
xx xK
и входного воздействия
()ut
позволяет однозначно
определить будущее поведение динамической системы. Эти переменные в
дальнейшем будем называть переменными состояния.
Способы задания переменных состояния могут быть разные. Обычно
используются либо те, которые дают преимущество в исследовании матема-
тической модели системы, либо те, которые имеют ясный физический смысл.
В случае наличия многомерной системы, имеющей
m
входов и
r
вы-
ходов, ее состояние в момент времени
t
, характеризуемое переменными со-
стояния
12
(), (), , ()
n
x
txt xtK
(рис.2.4), является функцией начального со-
стояния
12
(0), (0), , (0)
n
xx xK
и входных воздействий
12
(), (), , ()
m
ut u t u tK
, т.е.:
[
]
123 123
( ) (0), (0), (0), , (0); ( ), ( ), ( ), , ( )
ii n m
x
t x x x x ututut ut
ψ
= KK
,
где
i
ψ
- однозначные функции своих аргументов,
1, 2, ,in
=
K
.

63
Рис. 2.4. Представление многомерной системы в переменных состояния
Введем в рассмотрение понятие вектора состояния
()tx
:
[]
123
() (), (), (), , ()
T
n
t xtxtxt xt=x K
, (2.36)
где
T
обозначает транспонирование матрицы.
Размерность вектора состояния совпадает с порядком дифференциаль-
ного уравнения, описывающего динамические свойства системы.
Множество всех значений, которые может принять вектор
()tx
в мо-
мент времени
t
называется пространством состояния (фазовым простран-
ством), которое можно рассматривать как некоторое абстрактное
n
-мерное
векторное пространство. Точка, определяющая положение конца вектора со-
стояния
()tx
в пространстве состояний, называетея изображающей точкой.
Движение конца вектора состояния
()tx
в пространстве состояний
называется траекторией вектора состояния (фазовой траекторией).
Состояние системы, описываемой дифференциальным уравнением
первого порядка, характеризуется вектором состояния с одной переменной
состояния. Фазовое пространство в этом случае называется одномерным и
представляет собой линию на плоскости, а фазовая траектория - отрезок этой
линии (рис.2.5,а), который описывает конец вектора состояния от значения,
равного
0
()
x
t
в начальный момент времени
0
tt
=
до значения, равного
()
k
x
t
в конечный момент времени
k
tt
=
.
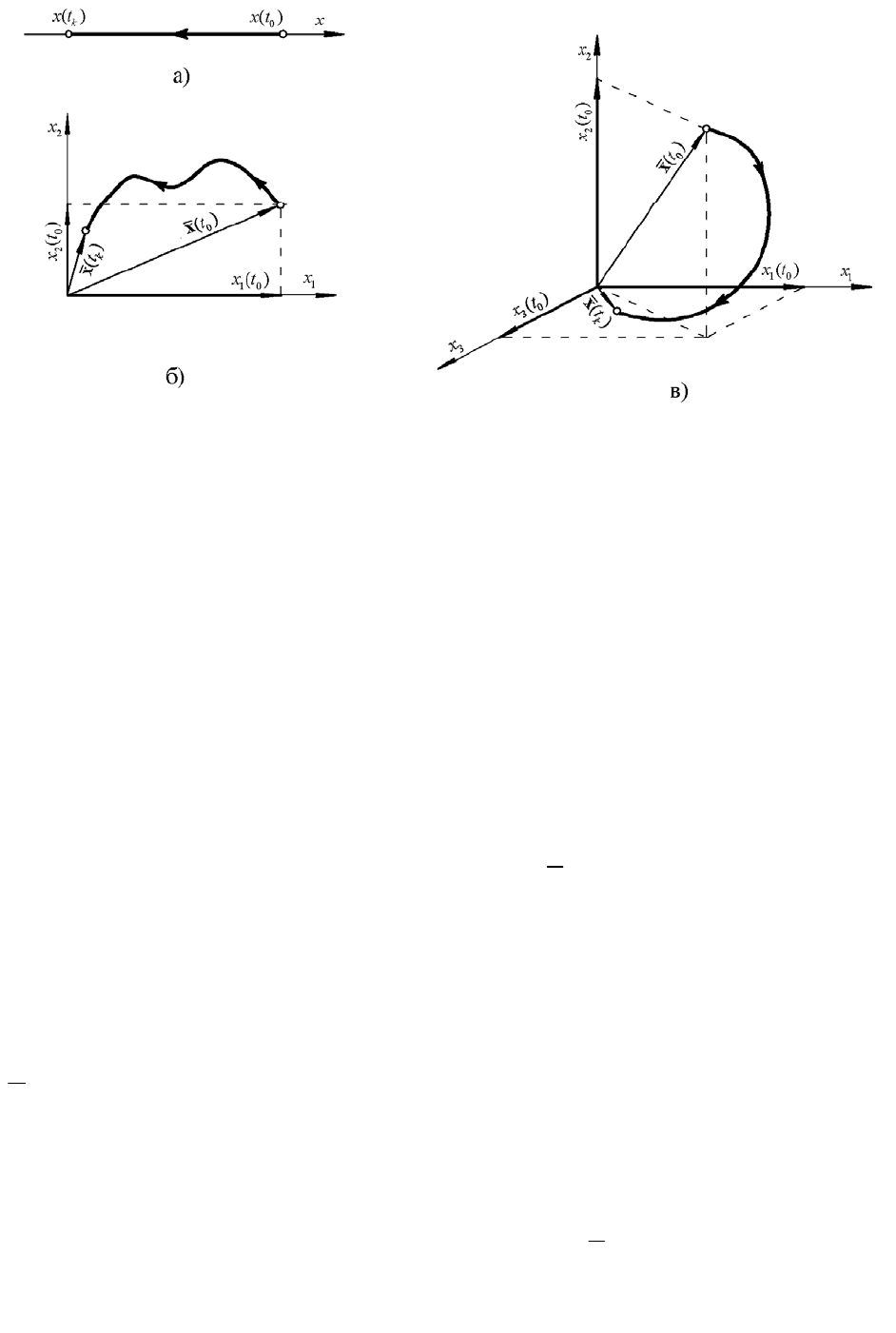
64
Рис.2.5. Фазовое пространство и фазовые траектории системы, описы-
ваемой дифференциальным уравнением:
а) - первого порядка;
б) - второго порядка;
в) - третьего порядка
Состояние системы второго порядка характеризуется вектором состоя-
ния с двумя переменными
1
()
x
t
и
2
()
x
t
. Фазовое пространство в этом слу-
чае называется двухмерным и представляет собой плоскость с прямоуголь-
ными координатами
1
x
,
2
x
, а фазовая траектория - кривая на плоскости,
которую описывает конец вектора состояния
()tx
при изменении времени
от
0
tt=
до
k
tt=
(рис.2.5.б).
На рис. 2.5,в показаны фазовая траектория в трехмерном фазовом про-
странстве с системой координат
1
x
,
2
x
,
3
x
и положение вектора состояния
0
()tx
для момента времени
0
tt
=
. Трехмерное фазовое пространство ис-
пользуется для характеристики движений системы третьего порядка. Для
системы
n
-го порядка переменные состояния
12
(), (), , ()
n
x
txt xtK
рас-
сматриваются как координаты вектора состояния
()tx
в
n
-мерном фазовом
пространстве.

65
По аналогии с пространством состояний для многомерной системы
управления вводятся пространство управлений (входов) и пространство
выходов. При этом управляющие воздействия
12
(), (), , ()
m
ut u t u tK
и
управляемые координаты
12
(), (), , ()
r
yt y t y tK
рассматриваются как коор-
динаты вектора управления
[]
12
() (), (), , ()
T
m
tutut ut=u K
в
m
-мерном
пространстве и координаты вектора выхода
[]
12
() (), (), , ()
T
r
tytyt yt=y K
в
r
-мерном пространстве соответственно.
Следует отметить принципиальное различие, вкладываемое в содержа-
ние понятий векторов управления
()tu
, выхода
()t
y
и вектора состояния
()tx
. Все составляющие
12
(), (), , ()
m
ut u t u tK
и
12
(), (), , ()
r
yt y t y tK
векторов
()tu
и
()t
y
являются конкретными физическими величинами. Век-
тор же состояния системы
()tx
является некоторой, в общем случае абст-
рактной, характеристикой системы.
Если на систему действуют помехи, характеризуемые вектором помех
[]
12
() (), (), , ()
T
l
tftft ft=f K
, то в этом случае вводится
l
-мерное простран-
ство помех.
Чтобы связать последовательные состояния системы во времени, ис-
пользуются дифференциальные уравнения:
[]
[]
[]
1 112 12
2 212 12
12 12
() (), (), , (); (), (), , (); ,
( ) ( ), ( ), , ( ); ( ), ( ), , ( ); ,
( ) ( ), ( ), , ( ); ( ), ( ), , ( );
nm
nm
nn n m
x
txtxtxtutututt
x
t xtxt xtutut utt
x
txtxtxtutututt
ϕ
ϕ
ϕ
⎫
′
=
⎪
′
⎪
=
⎪
⎬
⎪
⎪
′
=
⎪
⎭
KK
KK
KKKKKKKKKKKKKKKKKKKKKKKK
KK
. (2.37)
Правые части этих уравнений зависят от искомых функций
()
i
x
t
и не
зависят от их производных. Система уравнений первого порядка вида (2.37)
называется системой
n
дифференциальных уравнений, записанной в нор-
мальной форме Коши.
66
В общем случае число выходов (см. рис.2.4)
12
(), (), , ()
r
yt y t y tK
не
зависит от числа
n
переменных состояния - как правило, число переменных
состояния больше числа интересующих исследователя физических выходных
переменных, и тем более больше числа управляемых переменных. Знание
переменных состояния позволяет найти любой из выходных сигналов
()
i
y
t
как некоторые функции
12
,,,
r
gg gK
от переменных состояния и входов:
[]
[]
[]
1112 12
2212 12
12 12
() (), (), , (); (), (), , (); ,
( ) ( ), ( ), , ( ); ( ), ( ), , ( ); ,
( ) ( ), ( ), , ( ); ( ), ( ), , ( );
nm
nm
rr n m
yt gxtxt xtutut utt
yt gxtxt xtutut utt
yt gxtxt xtutut utt
⎫
=
⎪
=
⎪
⎬
⎪
⎪
=
⎭
KK
KK
KKKKKKKKKKKKKKKKKKKKKKKK
KK
. (2.38)
При этом правые части уравнений (2.37) и (2.38) (функции
12 12
,,,;,,,
nr
gg g
ϕ
ϕϕ
KK
) - являются однозначными функциями.
Системы уравнений (2.37) и (2.38) определяет состояние динамической
системы в любой момент времени
t
и называется уравнениями состояния.
В общем случае как дифференциальные уравнения (2.37) так и алгеб-
раические уравнения (2.38) являются нелинейными. В дальнейшем полагаем,
что эти уравнения линеаризованы и, кроме того, они описывают динамиче-
ские процессы в детерминированных стационарных системах. Напомним, что
в детерминированной системе каждому заданному вектору входа
()tu
соот-
ветствует единственный вектор выхода
()t
y
, а в стационарной системе ее
переменные состояния
()
i
x
t
, а также выходные переменные
()
i
yt
не зависят
от момента
0
t
приложения входных воздействий
()
k
ut
. При принятых допу-
щениях уравнения (2.37) и (2.38) могут быть преобразованы к следующему
виду:
1111122 1 111122 1
2 21 1 22 2 2 21 1 22 2 2
11 2 2 11
() () () () () () ();
() () () () () () ();
() () () () ()
nn mm
nn mm
nn n nnnn
x
taxtaxt axtbutbut but
x
taxtaxt axtbutbut but
xt axt axt axt but b
′
= + ++ + + ++
′
= + ++ + + ++
′
=+ ++ ++
KK
KK
KKKKKKKKKKKKKKKKKKKKKKKK
K
22
() ()
nnmm
ut bu t
⎫
⎪
⎪
⎪
⎬
⎪
⎪
++
⎪
⎭
K
. (2.39)

67
1111122 1 111122 1
2211222 2 211222 2
11 2 2 11 2
() () () () () () ();
() () () () () () ();
() () () () ()
nn mm
nn mm
rr r rnnr r
y
tcxtcxt cxtdutdut dut
y
t cxt cxt cxt dut dut d u t
yt cxt cxt cxt dut du
= + ++ + + ++
= + ++ + + ++
=+ ++++
KK
KK
KKKKKKKKKKKKKKKKKKKKKKKK
K
2
() ()
rm m
tdut
⎫
⎪
⎪
⎬
⎪
⎪
++
⎭
K
. (2.40)
В уравнениях (2.39) и (2.40)
ij
a
,
1, 2, ,in
=
K
;
1, 2, ,
j
n= K
;
ij
b
,
1, 2, ,in= K
;
1, 2, ,
j
m= K
;
ij
c
,
1, 2, ,ir
=
K
;
1, 2, ,jn= K
;
ij
d
,
1, 2, ,ir= K
;
1, 2, ,jm
=
K
; - постоянные коэффициенты, которые получают-
ся в результате разложения нелинейных функций
i
ϕ
и
i
g
в ряд Тейлора
при линеаризации уравнений.
В векторно-матричной форме записи уравнения (2.39), (2.40) имеют
следующий вид:
() () ()ttt
′
=
+xAxBu
; (2.41)
() () ()ttt
=
+yCxDu
, (2.42)
где
11 12 1
21 22 2
12
n
n
nn nn
aa a
aa a
aa a
=A
K
K
K KKK
K
;
11 12 1
21 22 2
12
m
m
nn nm
bb b
bb b
bb b
=B
K
K
KKKK
K
11 12 1
21 22 2
12
n
n
rr rn
cc c
cc c
cc c
=C
K
K
KKKK
K
;
11 12 1
21 22 2
12
m
m
rr rm
dd d
dd d
dd d
=D
K
K
KKKK
K
.
Уравнения (2.41) и(2.42) можно представить в виде структурной схемы,
приведенной на рис. 2.6.

68
Рис. 2.6. Структурная схема многомерной линейной стационарной сис-
темы
Так как элементы матриц
A
,
B
,
C
и
D
- постоянные числа, то и
сами эти матрицы также постоянны. Квадратная матрица
A
размерности
nn×
называется матрицей состояния - структура этой матрицы определяет
характер как свободных, так и вынужденных движений системы.
Матрица
B
размерности
nm
×
называется матрицей управляющих
воздействий. Ее структура определяет характер связи входа системы с раз-
личными переменными состояния. Матрица
C
размерности
rn×
называ-
ется матрицей выходных координат - ее структура определяет характер свя-
зи выходных координат системы с отдельными переменными состояния.
Матрица
D
размерности
rm
×
характеризует прямую (не динамическую)
связь выходных координат с управляющими координатами; ее структура оп-
ределяет, каким образом задающие функции на входе непосредственно воз-
действуют на различные составляющие выхода. Для многих физических сис-
тем матрица
D
является нулевой.
При векторно-матричной записи дифференциальных уравнений основ-
ными звеньями структурной схемы, как видно из рис. 2.6, являются много-
мерные сумматоры, интеграторы и матричные блоки
A
,
B
,
C
,
D
. По-
скольку определяемые элементами схемы операции линейны, а коэффициен-
ты матричных блоков постоянны, то схема линеаризованной модели на
рис.2.6 соответствует линейной стационарной системе. Эта же структурная

69
схема при замене матричных блоков с постоянными матрицами на матрич-
ные блоки с переменными матрицами
()tA
,
()tB
,
()tC
и
()tD
будет
соответствовать линейной нестационарной системе.
2.2.1. Стандартная форма записи уравнений состояния
Пусть известно нормированное (
0
1a
=
) дифференциальное уравнение
вход - выход, устанавливающее связь между выходом
()yt
и входом
()ut
одномерной системы
n
-го порядка:
() ( 1)
110
() () () () ()
nn
nn
ytay t aytaytbut
−
−
′
++++=K
. (2.43)
Определим уравнения состояния, соответствующие дифференциально-
му уравнению (2.43). Поскольку знание начальных значений выходной пере-
менной и ее производных
(1)
(0), (0), , (0)
n
yy y
−
′
K
полностью определяет бу-
дущее движение системы, то переменные
(1)
(), (), , ()
n
yt y t y t
−
′
K
могут быть
приняты в качестве переменных состояния:
1
21
(1)
1
() ();
() () ();
() () ()
n
nn
xt yt
xt yt xt
x
ty txt
−
−
=
⎫
⎪
′
′
==
⎪
⎬
⎪
⎪
′
==
⎭
KKKKKKKKK
. (2.44)
Разрешив уравнение (2.43) относительно старшей производной, имеем
() ( 1)
110
() () () () ()
nn
nn
yt ay t aytaytbut
−
−
′
=− − − − +K
. (2.45)
Тогда из (2.44) и (2.45) получаем следующую систему дифференциаль-
ных уравнений первого порядка относительно переменных состояния
12
(), (), , ()
n
x
txt xtK
и алгебраическое уравнение, связывающее выход сис-
темы
()yt
с соответствующей переменной состояния:

70
12
23
1
112 1 0
1
() ();
() ();
() ();
() () () () ();
() ()
nn
nnn n
xt x t
xt xt
xtxt
xt axt a xt axt but
yt x t
−
−
′
=
⎫
⎪
′
=
⎪
⎪
⎪
⎬
′
=
⎪
⎪
′
=− − − − +
⎪
=
⎪
⎭
KKKKKKKKKKKKKKKKKKK
K
(2.46)
Систему уравнений (2.46) удобно записать в векторно-матричной фор-
ме следующим образом:
[]
[]
11
22
11
123 1 0
12
() 0 1 0 0 0 () 0
() 0 0 1 0 0 () 0
.. . ... 0
();
() 0 0 0 0 1 ()
() ()
() 1 0 0 0 () () ()
nn
nnnnn n
T
n
xt xt
xt xt
ut
xt xt
xt a a a a a xt b
yt x t x t x t
−−
−− −
′
⎫
⎪
′
⎪
⎪
=+
⎪
⎬
′
⎪
′
−− − − −
⎪
⎪
=⋅
⎪
⎭
K
K
KK KK
KM
K
KK
. (2.47)
или
() () (),
() ()
ttut
yt t
′
=+
⎫
⎬
=
⎭
xAxB
Cx
, (2.48)
где согласно (2.47) матрица состояния
A
размерности
nn×
, матрица входа
B
размерности
1n ×
, матрица выхода
C
размерности
1 n×
и вектор со-
стояния
()tx
размерности
1n
×
равны:
[]
[]
123 1 0
12
01 0 0 0 0
00 1 0 0 0
.. . ... 0;;
00 0 0 1
100 0; () () () ()
nn n n
T
n
aa a a a b
txtxt xt
−− −
⎫
⎡⎤⎡⎤
⎪
⎢⎥⎢⎥
⎪
⎢⎥⎢⎥
⎪
⎢⎥⎢⎥
==
⎪
⎢⎥⎢⎥
⎬
⎢⎥⎢⎥
⎪
⎢⎥⎢⎥
−− − − −
⎪
⎣⎦⎣⎦
⎪
==
⎪
⎭
AB
Cx
K
K
KM
K
KK
. (2.49)
Уравнения (2.46) называются уравнениями состояния в стандартной
форме.
Пример 2.5.
