Абраменко И.Г. Теория автоматического управления

Подождите немного. Документ загружается.

00 0

lim ( )

()

lim ( ) lim ( ) lim ( ) ( ) lim

lim lim

rrr

ts s s

kW s

yt sY s sW sX s s kx

sss

→

→∞ → → →

→→

== = = =

Таким образом, только при

между величинами

)(

∞

суще-

ствует определенная однозначная зависимость вида:

)(lim kxty

∞→

При

0r >

такая зависимость отсутствует.

Пример 2.2.

Пусть система описывается уравнением вида

012

ay ay ay kx

′

′′

Требуется найти передаточную функцию

()Ws

системы при

1k =

1a =

3a =

2a =

Решение.

Преобразуем уравнение системы по Лапласу при нулевых начальных

условиях. Получим

012

()()()as as a Y s kX s++ =

. Откуда передаточная функ-

ция будет:

012

() 1

()

() 3 2

Ys k

Xs as as a s s

== =

++ ++

***

2.1.3. Линеаризация уравнений САУ

Уравнения многих реальных элементов и САУ в целом в той или иной

мере являются нелинейными. В этом случае переменные

)(tx

)(ty

и их про-

изводные входят в выражение для функции

в виде произведений, частных,

степеней либо других более сложных функций. Рассмотрим пример.

Пример 2.3.

Составим математическую модель ДПТ с независимым возбуждением,

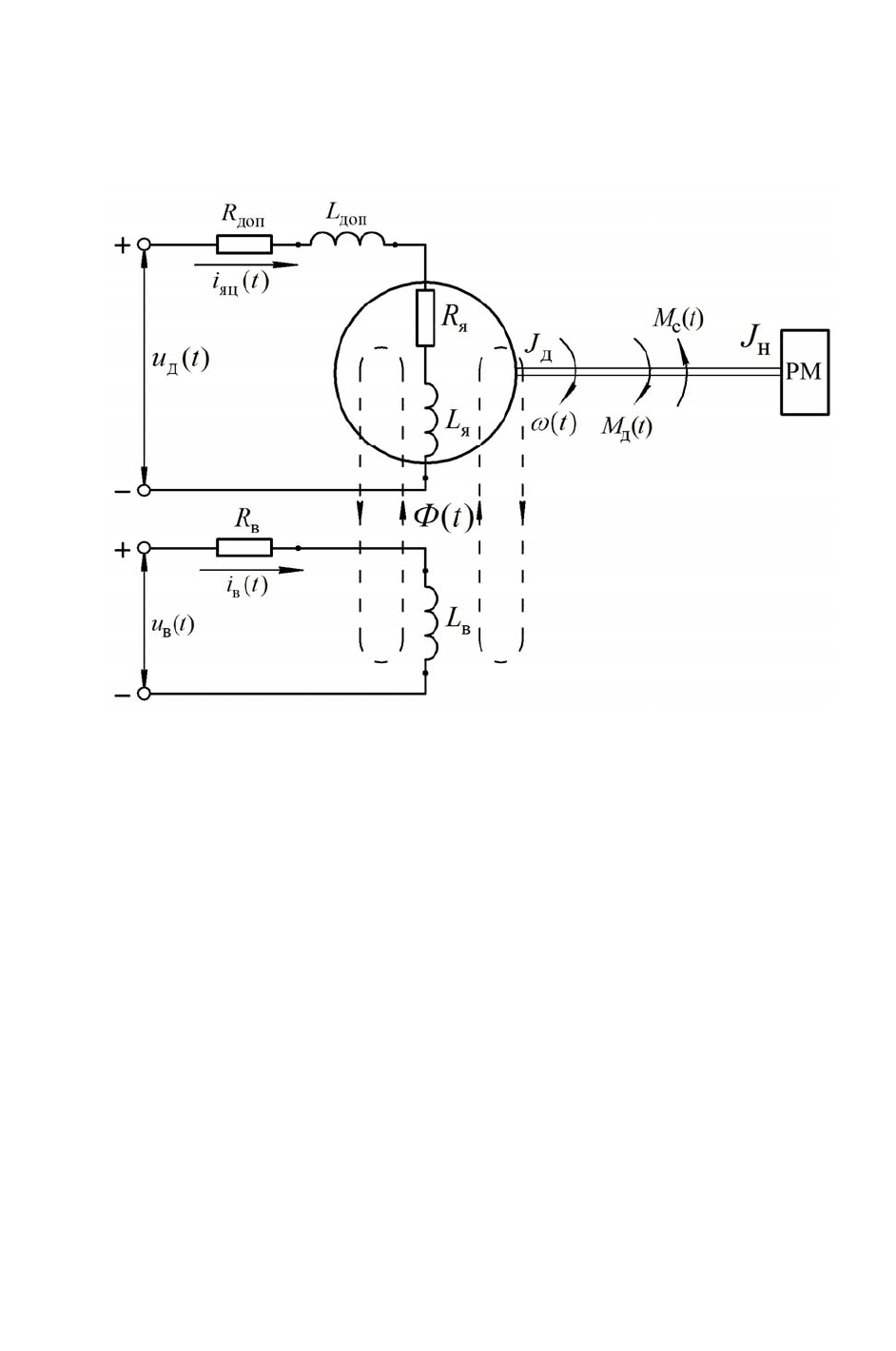
принципиальная схема которого приведена на рис. 2.1.

Рис. 2.1. Принципиальная схема ДПТ:

- соответственно, активное сопротивление и индуктив-

ность якорной обмотки;

доп

- активное сопротивление и

индуктивность дополнительных элементов якорной цепи (щеток,

дополнительных полюсов и т.д.);

яц

()it

- ток якорной цепи;

()it

- соответственно, ток, активное сопротивление и индук-

тивность обмотки возбуждения;

- моменты инерции яко-

ря двигателя и нагрузки;

()t

- угловая скорость вращения вала

якоря;

()

- момент, развиваемый двигателем;

()Ф t

- магнит-

ный поток полюсов.

Решение.

Математическую модель двигателя определим для общего случая

управления как по цепи якоря, осуществляемого с помощью изменения на-

пряжения

()ut

, так и по цепи возбуждения, осуществляемого с помощью

изменения напряжения возбуждения

()ut

, при действии на двигатель воз-

мущения в виде момента сопротивления

()

имеющейся нагрузки.

Поэтому в качестве входных сигналов примем

()ut

()

, а в

качестве выходного -

()t

Сделаем допущения, что:

- параметры

доп

являются постоянными;

- связь рабочего механизма с валом двигателя осуществляется без зазо-

ра (люфта) и является абсолютно жесткой;

- приведенный к валу двигателя момент сопротивления не зависит от

скорости;

- влияние вихревых токов в станине и полюсах двигателя, а также вязкого

(скоростного) трения равно нулю.

Физику процессов в ДПТ на основе данных литературных источников

можно описать следующей системой уравнений:

- уравнением электрического равновесия для цепи обмотки якоря

яц

дд яц

()

() () ()

di t

ut t Ri t L

ΣΣ

=+ +

; (2.9)

- уравнением электрического равновесия для цепи обмотки возбужде-

ния

вввв

()

() ()

di t

ut Rit L

; (2.10)

- уравнением кривой намагничивания (гистерезис не учитывается);

() [ () ]Ф t

it w

⋅

; (2.11)

- уравнением движения

дс

()

() ()

JMtMt

=−

. (2.12)

Здесь

ддоп

RRR

ддоп

дн

JJJ

- количе-

ство витков обмотки возбуждения.

Как известно, противоЭДС двигателя

()te

определяется соотноше-

нием:

() () ()tc tФ te

⋅⋅

, (2.13)

а его вращающий момент соотношением:

дяц

() () ()Mt с itФ t

⋅⋅

. (2.14)

где

(2 )cpN a

- машинная постоянная;

- число пар полюсов;

число эффективных проводов якоря;

- число параллельных ветвей обмот-

ки якоря.

Подставив (2.10) и (2.11) в (2.6) и (2.9), получим систему:

яц

дяц

вввв

яц с

()

() () () () ;

()

() () ;

() [ () ];

()

() () ()

di t

ut c tФ tRitL

di t

ut Rit L

Ф tfitw

J с itФ tMt

ΣΣ

⎫

=⋅ ⋅ + +

⎪

⎬

⎪

=⋅

⎪

=⋅ ⋅ −

⎪

⎭



(2.15)

Уравнения (2.13) и (2.14) содержат произведения функций, а уравнение

(2.11) по определению является нелинейным. Анализ и аналитическое реше-

ние нелинейных уравнений, а тем более систем является сложной и не всегда

выполнимой задачей. 1 L

Эффективным средством решения (2.15) является использование чис-

ленных методов. Для этого (2.15) удобно преобразовать к следующему виду:

яц

дяц

вв

яц с

()

() () () ();

()

() ();

() [ () ];

() 1

() () ()

di t

ut tФ tit

dt L L L

di t R

ut it

dt L L

Ф tfitw

dt с

itФ tMt

dt J J

ΣΣ Σ

ΣΣ

⎫

=−⋅⋅−

⎪

=−

⎪

⎬

⎪

=⋅

⎪

=⋅ ⋅ −

⎪

⎭



(2.16)

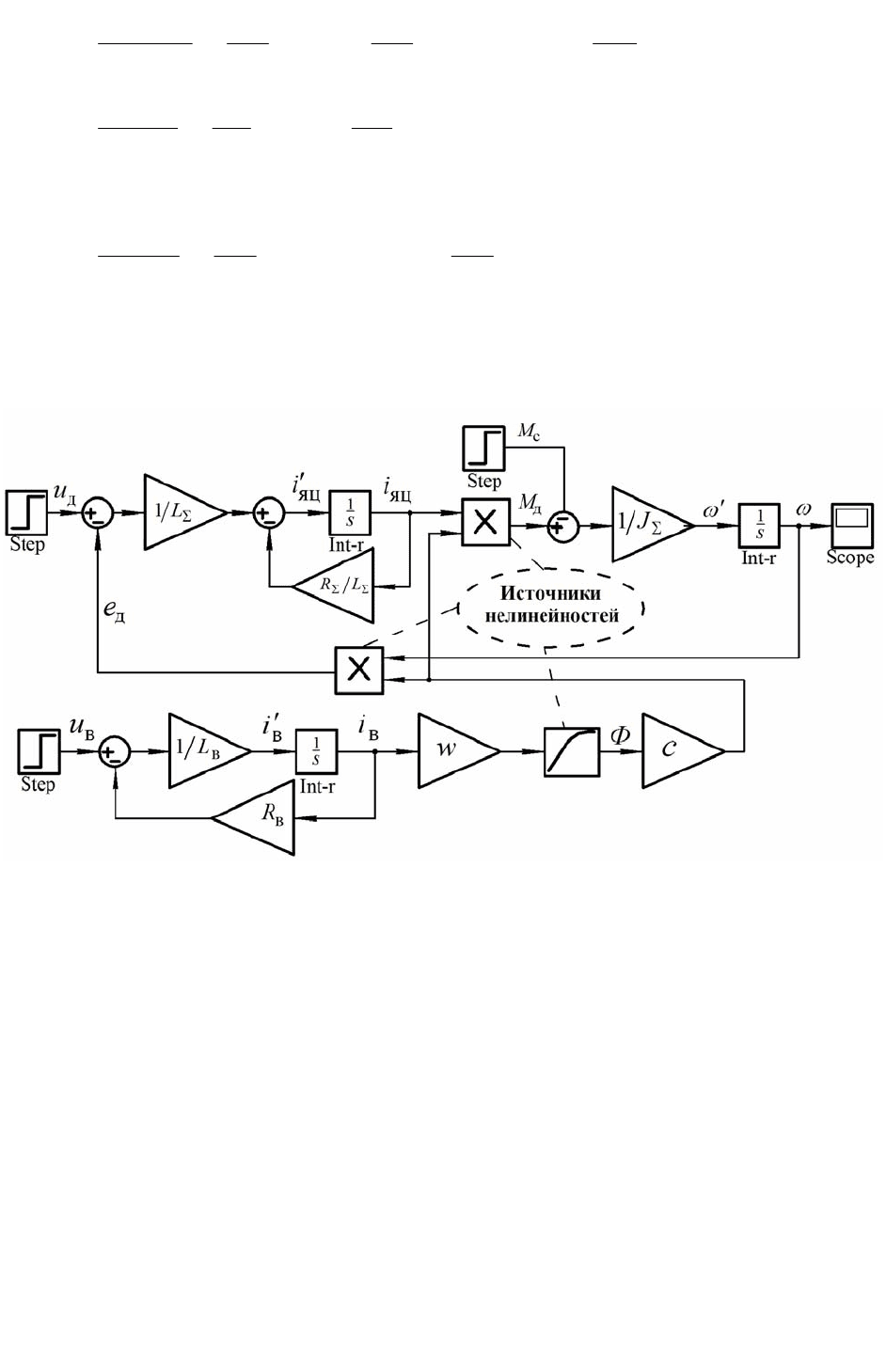
На рисунке представлена блок-схема реализации процесса решения

(2.16) средствами структурного программирования пакета Simulink.

Рис. 2.2. Реализация системы (2.13) средствами Simulink

Таким образом ДПТ с независимым возбуждением представляет собой

сложный объект, имеющий три входа - задающие

()ut

, а также

возмущающее воздействия

()

. Имеется отрицательная обратная связь по

скорости, роль которой выполняет противоЭДС двигателя

() () ()tcФ tte

=⋅ ⋅

По приведенной схеме можно проводить расчеты при определенных (в

общем-то, любых) параметрах входных сигналов и получать те или иные ча-

стные результаты. Поэтому такая модель может быть с успехом использована

на стадии окончательной проверки результатов выполняемого анализа либо

синтеза САУ. Однако применить многие апробированные методы линейной

ТАУ в этом случае невозможно.

***

В связи со сложностью анализа и решения нелинейных уравнений ши-

роко применяется приближенная их замена на линейные – линеаризация.

Существует несколько методов линеаризации. Наибольшее распростра-

нение получил метод малых отклонений, который позволяет линеаризовать

как нелинейные алгебраические характеристики отдельных элементов, под

которыми понимаются зависимости выходных величин от входных в устано-

вившемся режиме, так и нелинейные дифференциальные уравнения. Необхо-

димыми и достаточными условиями применения

метода являются следую-

щие два требования:

– отклонения изменяемых переменных от их установившихся значений в

течение всего процесса управления должны быть достаточно малы;

– функция

(

)

()

,,,, ,...,

Fxxyyy y

′′′′

, составляющая левую часть уравнения

(2.1), имеет непрерывные частные производные по всем своим аргументам в

окрестностях точки, соответствующей установившемуся режиму.

Достаточная малость отклонений переменных от установившихся зна-

чений обычно выполняется, чего требует сам принцип построения замкнутой

системы (принцип управления по отклонению).

В основу метода линеаризации положено разложение в ряд Тейлора,

позволяющее разложить нелинейную функцию нескольких переменных по

степеням малых отклонений этих переменных в окрестностях значений, со-

ответствующих заданному установившемуся режиму. В качестве установив-

шегося режима может выбираться режим, существовавший до начала дейст-

вия возмущения, либо режим,

который установится после затухания пере-

ходного процесса.

Рассмотрим нелинейное дифференциальное уравнение второго порядка

вида:

(

)

0,,,,,

′

yyyfxxF

. (2.17)

Производные

xyy

′′′′

будем считать самостоятельными переменными.

Тогда точка заданного установившегося режима может быть задана следую-

щими значениями аргументов:

(0)

;

(0)yy

;

(0) (0) (0) 0xyy

′

′′′

== =

Перепишем уравнение (2.17), воспользовавшись разложением Тейлора:

()

000

,0, , ,0,0 () [ ()] () ()

()

[ ( )] [ ( )] 0

() ( )

FF FF

xfy xt xt ft yt

xx fy

yt y t R

∂∂ ∂∂

′

+Δ+ Δ +Δ+Δ+

′

∂∂ ∂ ∂

∂∂

′′′

Δ+ Δ +=

′′′

∂∂

(2.18)

где:

() ()

txtxΔ= −

;

() ()

tftf

=−

;

() ()yt yt yΔ= −

;

[ ()] () () 0 ()

t xt x xt xt

′′′′ ′

Δ=−=−=

;

[()] ()

′

;

[()] ()yt yt

′′ ′′

– откло-

нения переменных от установившихся значений;

...,

)(

′

∂

– значения

частных производных, вычисленные в точке заданного установившегося ре-

жима;

– остаточный член разложения, содержащий различные произведе-

ния отклонений соответствующих аргументов, а также их степени, т.е. вели-

чины высших порядков малости.

Воспользовавшись условием о том, что отклонения переменных малы,

в разложении оставляем только члены, содержащие эти отклонения в первых

степенях, т.е. принимаем, что

≈

Вычтя из уравнения (2.18) уравнение установившегося режима

(

)

00,0,,,0,

000

yfxF

получаем окончательно:

0000 0

() [ ()] () () [ ()] [ ()] 0

() () ( )

FF FFF F

xt x t f t yt y t y t

xx fyy y

∂∂ ∂∂∂ ∂

′′′′

Δ+ Δ + Δ+ Δ+ Δ + Δ =

′′′′

∂∂ ∂ ∂∂ ∂

. (2.19)

Уравнение (2.19) не содержит нелинейных членов и является линей-

ным. Коэффициенты уравнения являются постоянными или переменными,

если установившийся режим характеризуется переменными во времени зна-

чениями

()

()yt

()

(программной траекторией).

Однако при этом следует учитывать, что в результате линеаризации

получается уравнение в отклонениях. Переменными уравнения (2.19) явля-

ются отклонения

()

tΔ

()ytΔ

, а не переменные

()

)(ty

, что соответст-

вует переносу начала координат в точку

установившегося режима.

В случае линеаризации нелинейной алгебраической характеристики ка-

кого-то элемента линеаризованное уравнение записывается также в отклоне-

ниях. Например, если

()

является нелинейной функцией аргумента

()

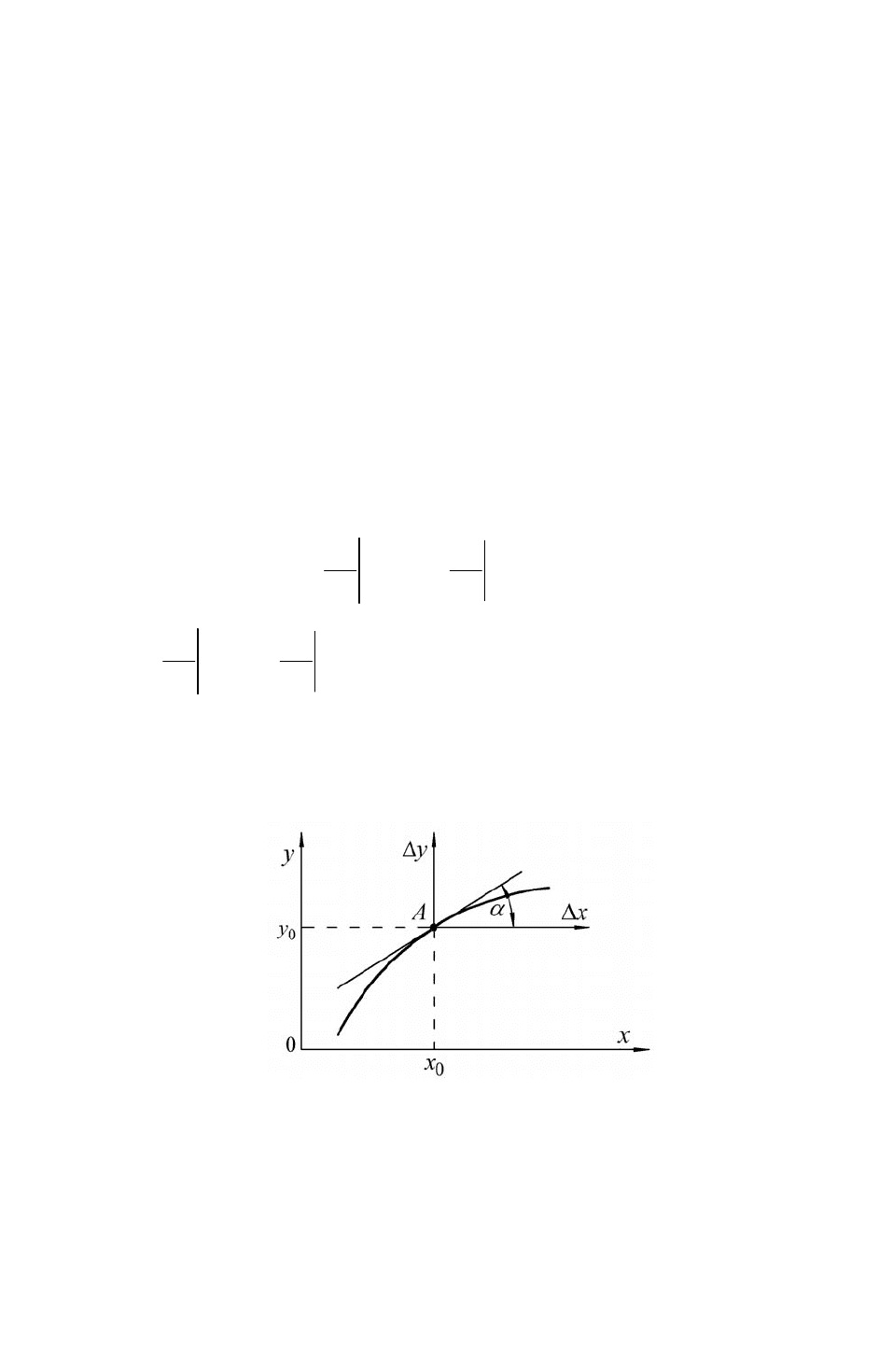
(см. рис. 2.3), то

(

)

(), () () [ ()]Fxt yt yt fxt=−

и линеаризованное уравнение

такого элемента имеет вид:

() () 0

yt xt

∂∂

−Δ=

∂∂

Учтя, что

∂

, где

- угол наклона касательной, прове-

денной к точке равновесия

[, ]

, окончательно получим:

() ()yt tg xt

=⋅Δ

. (2.20)

Рис.2.3. Геометрическая интерпретация линеаризации уравнений

Из рисунка видно, что чем меньше величины отклонений

()

, тем

точнее линеаризованное уравнение отображает процессы, описываемые ис-

ходным уравнением.

Заметим, что линеаризация недопустима в тех случаях, когда элемент

имеет существенно нелинейную статическую характеристику, например ре-

лейную. Линеаризация нелинейного уравнения в этом случае будет означать

искажение принципа работы этого элемента.

Пример 2.4

Произведем линеаризацию математической модели ДПТ с независимым

возбуждением из примера 2.3.

Решение.

Сначала линеаризуем уравнение (2.13). Запишем его следующим обра-

зом:

дд

(), (), () () () () 0Fet tФ tetctФ t

ωω

⎡⎤

−⋅ ⋅ =

⎣⎦

. (2.21)

Линеаризуем функцию (2.21) в окрестностях базовых значений пере-

менных

, соответствующих установившемуся режиму.

Имеем

() () () 0

FFF

et t Ф t

e Ф

∂∂∂

⋅Δ + ⋅Δ + ⋅Δ =

∂∂∂

. (2.22)

Согласно (2.21)

∂

c Ф

∂

−⋅

∂

−⋅

∂

. (2.23)

Подставив выражения (2.23) в (2.22), получим:

д 00

() () ()et c Ф tcФ t

Δ=⋅⋅Δ+⋅⋅Δ

. (2.24)

Учтем, что

яц,0 яц

яц

()

di i t

di t

dt dt

⎡⎤

+Δ

⎣⎦

и запишем уравнение (2.9) в отклонениях:

яц

дд яц

()

() () ()

di t

ut t R i t L

ΣΣ

Δ=Δ+Δ+

; (2.25)

Преобразовав (2.25) и (2.24) по Лапласу и исключив промежуточную

переменную

()EsΔ

, получим:

0 яц д 0

() 1 () () ()

c Ф sR sIs Usc Ф s

⎛⎞

⋅⋅ΔΩ+ + Δ =Δ −⋅⋅Δ

⎜⎟

⎝⎠

. (2.26)

Линеаризуем уравнение (2.14). Запишем его следующим образом:

дяц д яц

(), (), () () () () 0FM ti tФ tMtcitФ t

⎡⎤

−⋅ ⋅ =

⎣⎦

. (2.27)

Линеаризуем функцию (2.27) в окрестностях базовых значений пере-

менных

д,0

ц,0

, соответствующих установившемуся режиму:

Согласно (2.27)

∂

яц

сФ

∂

=−

∂

ц,0

с i

∂

−⋅

∂

. (2.28)

Подставив выражения (2.28) в (2.27), получим:

д 0 яц яц,0

() () ()Mt cФ it ci Ф tΔ=⋅⋅Δ+⋅⋅Δ

. (2.29)

Запишем в отклонениях уравнение (2.12):

дс

()

() ()

JMtMt

=Δ −Δ

. (2.30)

Преобразовав (2.29) и (2.30) по Лапласу и исключив промежуточную

переменную

()

sΔ

, получим:

0 яц яц,0 с

() () () ()Js s cФ Is ci Ф sMs

⋅

⋅ΔΩ − ⋅ ⋅Δ = ⋅ ⋅Δ −Δ

. (2.31)

Исключим из уравнений (2.26) и (2.31) отклонение потока

()Ф sΔ

и от-

клонение тока

яц

()Is

Для этого воспользуемся зависимостью между потоком

()Ф t

и током

возбуждения

()it

, которая определяется кривой намагничивания (2.11) и

также является нелинейной.