Абраменко И.Г. Теория автоматического управления

Подождите немного. Документ загружается.

ры). Сигнал

()utΔ

усиливается в УПТ и поступает на вход ТП. В результате

на якорной обмотке двигателя формируется напряжение. Величина

()tu

за-

висит от величины сигнала рассогласования и передаточных коэффициентов

тиристорного преобразователя

тп

и усилителя постоянного тока

упт

дупттп упттпп

() () ()utkk utkkk t

⋅⋅Δ = ⋅⋅⋅Δ

Тиристорный преобразователь ТП, двигатель М и редуктор А образуют

исполнительный блок. Выходным сигналом этого блока является скорость

вращения выходного вала редуктора

, которая является управляющим

воздействием на РМ.

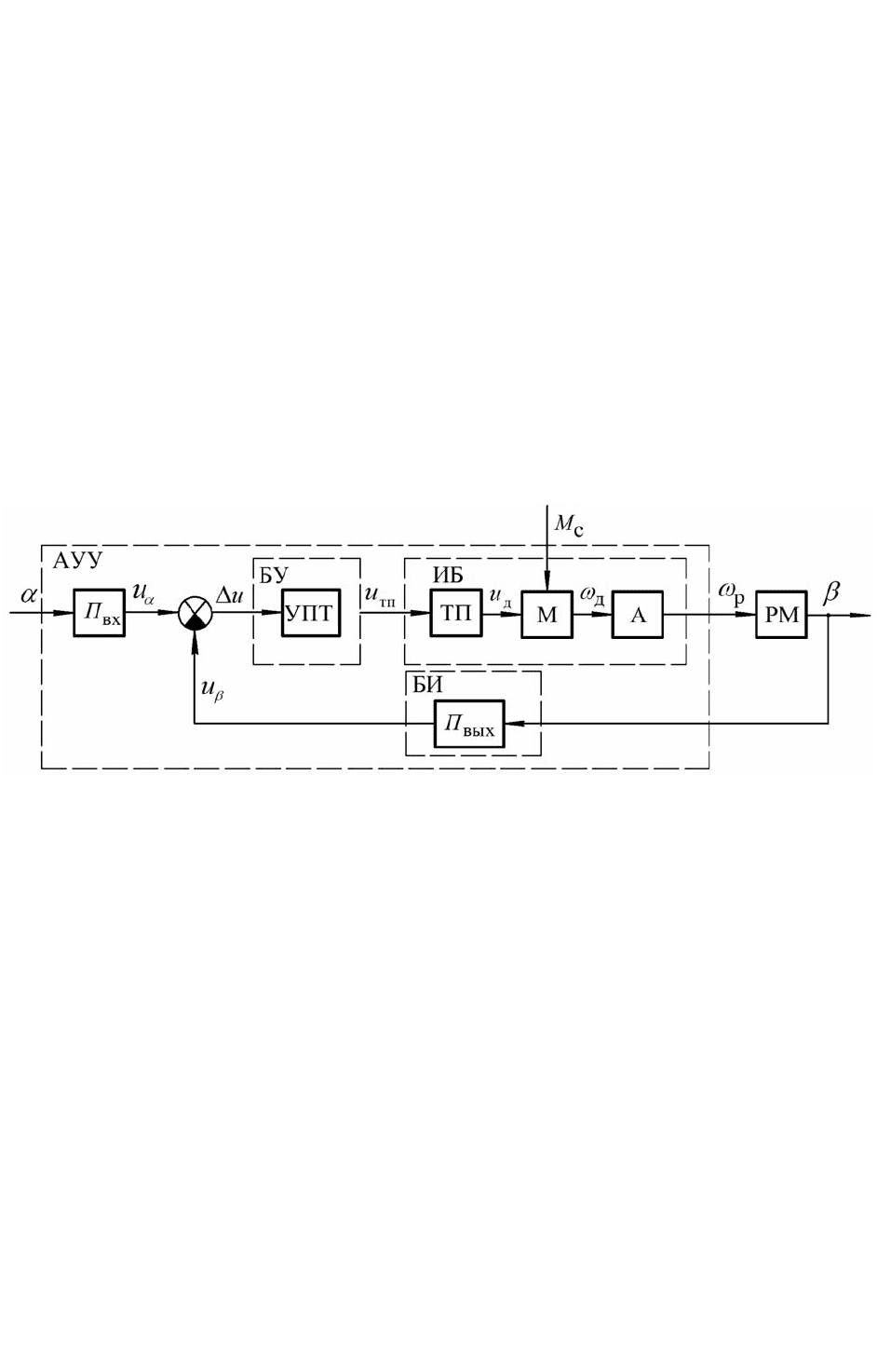
Функциональная схема системы приведена на рис. 1.17.

Рис. 1.17

Рассмотрим работу системы. При идентичном положении командной и

исполнительной осей угол рассогласования между ними равен нулю. Также

равны нулю напряжения

uΔ

, т.е. двигатель и вся система находятся в

покое. При повороте командной оси на некоторый угол возникает угол рас-

согласования

αβ

=−

и пропорциональные ему напряжения. Под воз-

действием напряжения

двигатель начинает вращаться и через редуктор

поворачивает исполнительную ось и движок потенциометра

вых

в сторону

уменьшения угла рассогласования до тех пор, пока этот угол не станет рав-

ным нулю. При повороте командной оси в другую сторону меняется поляр-

ность напряжения, прикладываемого к двигателю, и, следовательно, направ-

ление его вращения.

***

Контрольные вопросы

1. Назовите задачи, которые решаются в курсе теории автоматического

управления.

2. Какую роль играет автоматизация на современном этапе развития

науки и техники?

3.Укажите преимущества и недостатки принципов управления, приме-

няемых в САУ.

4. Что такое функциональная схема САУ?

5. На какие классы делятся САУ по цели управления?

6. На какие классы делятся САУ по виду математического описания?

7. Что такое переходный процесс?

8. Какие типовые воздействия используются при изучении динамики

элементов и систем?

9. Какие признаки элементов системы управления отражаются на ее

функциональной схеме?

10. Назовите наиболее распространенные функциональные элементы

систем управления.

11. На какие классы разделяются системы управления по величине

ошибки

()Δ∞

в установившемся режиме?

12. На какие классы разделяются системы управления по принципу

действия?

13. Какие преимущества и недостатки имеют разомкнутые системы

управления?

14. Какие преимущества и недостатки имеют замкнутые системы

управления?

Глава 2. Математическое описание САУ

Решение вопросов анализа существующих и синтеза новых САУ воз-

можно лишь при наличии соответствующего математического описания их

свойств. Это описание называют математической моделью САУ, так как при

ее составлении всегда делаются те или иные допущения и приближения.

Отметим, что одна и та же система в зависимости от целей исследования

может описываться несколькими различными моделями. Это объясняется

противоречивостью требований к моделям: с одной стороны они должны как

можно полнее отражать свойства оригинала, а с другой стороны – быть по

возможности

проще в использовании. Однако все модели САУ обычно явля-

ются дифференциальными уравнениями и только отдельные элементы могут

характеризоваться алгебраическими соотношениями.

При математическом описании САУ применяются два подхода: первый

из них основывается на представлении моделей в переменных вход – выход, а

другой – в переменных состояния.

Представление в переменных вход – выход основано на описании

свойств САУ дифференциальными уравнениями произвольного порядка.

Модель в переменных состояния использует

систему дифференциаль-

ных уравнений только первого порядка, разрешенных относительно первых

производных, т.е. уравнений в нормальной форме Коши. Такая система, за-

писанная в векторно–матричной форме, обычно называется уравнениями со-

стояния.

2.1. Математическое описание в переменных вход – выход

Математическое описания системы составляют на основе описания

всех входящих в нее элементов. Первым шагом в составлении модели от-

дельного элемента САУ является выявление физических законов, опреде-

ляющих его поведение. Математические выражения этих законов и является

искомой моделью. Затем, путем исключения промежуточных переменных,

получают модель САУ в целом.

Для САУ, имеющей один вход

()

и один выход

)(ty

, математиче-

скую модель можно представить в виде:

(

)

()

(), (), (), (), (),..., () 0

Fxtxtytytyt y t

′′′′

. (2.1)

Уравнение (2.1) называют уравнением динамики, так как оно учитывает

входящие переменные в виде функций времени. Уравнение динамики опи-

сывает физические процессы в системе как в установившихся, так и в пере-

ходных режимах при любых внешних воздействиях. Воспользовавшись (2.1),

можно проводить анализ свойств системы, в частности, можно определять

степень устойчивости, точность, количественные показатели

переходных

процессов.

Уравнение динамики, если в нем все производные положить равными

нулю, превращается в уравнение статики:

(

)

00,...,0,0,,0,

yxF

. (2.2)

Уравнение статики описывает физические процессы в системе в ус-

тановившемся режиме при постоянных внешних воздействиях. Обычно это

уравнение является алгебраическим. Из уравнения статики замкнутой систе-

мы может быть определена, в частности, статическая ошибка системы.

Сказанное справедливо для случая, когда уравнение (2.1) содержит по-

мимо производных выходной величины и саму выходную величину

)(ty

Если же

)(ty

отсутствует, то для получения из уравнения динамики уравне-

ния статики нужно принять все производные равными нулю, кроме произ-

водной

)(ty

самого низкого порядка. В этом случае уравнение статики ус-

танавливает связь между этой производной и входным воздействием.

Для линейной стационарной САУ уравнение (2.1) является линейным

неоднородным дифференциальным уравнением вида:

() ( 1) ( ) ( 1)

01 01

() () () () () ()

nn mm

ay t ay t ayt bu t bu t but

−−

+++=+++KK

, (2.3)

где

()ut

)(ty

– соответственно, входная и выходная величины, изменяю-

щиеся во времени;

– постоянные коэффициенты, определяемые пара-

метрами системы;

– порядок уравнения.

Для определения решения уравнения (2.3) необходимо задать

на-

чальных условий (значений выходной величины и ее производных при

0t =

() (0)yt y=

() (0)yt y

′

,…,

(1) (1)

() (0)

yty

−−

(2.4)

и вид входной величины

()ut

Одной из основных особенностей линейных систем является то, что к

ним применим принцип суперпозиции, в соответствии с которым реакция сис-

темы на совокупность возмущений определяется суммой реакций на каждое

возмущение в отдельности. Эта особенность имеет большое практическое

значение, так как в этом случае значительно упрощаются многие расчеты.

2.1.1. Стандартная форма записи дифференциальных уравнений

САУ

При исследовании САУ, особенно при сравнении свойств систем и их

элементов между собой, удобно представлять уравнения в т.н. стандартной

форме. При этом используются следующие правила:

– выходную величину и все ее производные записывают в левой части

уравнения, а все остальные члены – в правой;

– коэффициент при выходной величине путем тождественных

преобра-

зований делают равным единице;

– если в правой части содержатся производные, то члены, содержащие

определенную выходную величину и ее производные, объединяют в одну груп-

пу и коэффициент при этой величине выносят за скобки.

Пример 2.1.

Исходное уравнение системы имеет вид:

)()()()()()(

010210

tfctubtubtyatyatya +

′

′′

Представим это уравнение в стандартной форме.

Решение.

Имеем:

000

22 21 2

() () () () () ()

abc

yt yt yt ut ut ft

aa ab a

⎡⎤

′′ ′ ′

++= ++

⎢⎥

⎣⎦

Введем обозначения:

020

Taa =

;

121

Taa

;

121

kab =

;

210

Tbb

;

220

kac =

Тогда:

[

]

01 12 2

() () () () () ()Tyt Tyt yt kTut ut kft

′′ ′ ′

++= ++

Коэффициенты

имеют размерность времени, т.к.

[][]

[

]

[

]

[]

[

]

[]

[

]

[

]

[]

⎭

⎬

⎫

⎩

⎨

⎧

⋅

и называются постоянными времени. Их значения определяют скорость и ха-

рактер протекания переходных процессов.

Коэффициенты

называются коэффициентами передачи, имеют

размерность

[][][]

kyu=

[

]

[

]

[

]

fyk

и определяют взаимосвязь перемен-

ных в установившихся статических режимах.

***

Если же исходное уравнение не содержит каких–то коэффициентов,

например,

, то в стандартной форме единице должен равняться коэф-

фициент при производной, имеющей меньший порядок. При этом размер-

ность коэффициентов передачи будет меняться, а их значения будут опреде-

лять взаимосвязь переменных в соответствующих установившихся динами-

ческих режимах (например, в режиме с постоянной скоростью изменения

выходной величины).

2.1.2. Операционный метод описания линейных САУ

В математике под операционным исчислением подразумевается раздел

математического анализа, в котором разрабатываются методы решения ли-

нейных дифференциальных, разностных и некоторых типов интегральных

уравнений. Операционное исчисление базируется на идее замены одних

функций на другие, получаемые по определенным правилам, например, ис-

пользуя преобразование Лапласа или преобразование Фурье.

В ТАУ самое широкое применение

нашел операционный метод опи-

сания, основанный на использовании интегрального преобразования Лапласа

(L- преобразования):

{}

( ) () ()

s L ft ft dte

∞

−

∫

. (2.5)

Это преобразование устанавливает соответствие между функцией

)(tf

действительной переменной

и функцией

)(sF

комплексной переменной

. При этом

)(tf

называют оригиналом, а

)(sF

- изображением.

Достаточными условиями существования (2.5) являются следующие

требования:

- функция

)(tf

должна быть однозначной и непрерывной при всех

0≥t

, непрерывность может быть нарушена только в отдельных точках, яв-

ляющихся точками разрыва непрерывности первого рода;

- функция

0)( =tf

для всех

;

- функция

)(tf

должна иметь ограниченный порядок возрастания, т.е.

должны быть такие два постоянных числа

0>M

0>c

, при которых

()

ft Me<

при

0>t

2.1.2.1.

Основные свойства преобразования Лапласа

Преобразование Лапласа ставит в соответствие операциям над ориги-

налами некоторые определенные операции над изображениями. В таблице

2.1 приведены основные соотношения, используемые при описании линей-

ных САУ.

Таблица 2.1

Наименование свойства Оригинал Изображение

Линейность

()

af t

∑

sFa

)(

Дифференцирование оригинала

при нулевых начальных условиях

tfd )(

)(

)(sFs

Интегрирование оригинала при

нулевых начальных условиях

∫

)( dttf

sF )(

Изменение масштаба

)( tf

⎟

⎠

⎞

⎜

⎝

⎛

αα

Смещение аргумента оригинала

)(

−

()

Fse

−

Свертка функций

() ( )

ft d

ττ

−

∫

)()(

sFsF

Начальное значение оригинала

lim ( )

→

lim ( )

→∞

Конечное значение оригинала

lim ( )

→∞

lim ( )

→

2.1.2.2. Передаточная функция

Применение преобразования Лапласа при математическом описании

САУ обусловливается также и тем, что с его помощью определяют так назы-

ваемую передаточную функцию, которая является самой компактной формой

описания свойств САУ или ее составных элементов.

Пусть дано линейное неоднородное уравнение САУ

)()()()()()(

)1(

)(

)1(

)(

txbtxbtxbtyatyatya

+++=+++

−−

Преобразуем это уравнение по Лапласу при нулевых начальных усло-

виях:

)()()()()()(

sXbsXsbsXsbsYasYsasYsa

+++=+++

−−

. (2.6)

Воспользовавшись (2.6), можем записать:

)(

asasa

bsbsb

+++

−

. (2.7)

Анализ выражения (2.7) показывает, что соотношение

)()( sXsY

не за-

висит от вида входного воздействия

)(tx

, а характеризует только собствен-

ные свойства САУ. Это соотношение и называется передаточной функцией

и обозначается

)(sW

Таким образом, передаточной функцией называется отношение вы-

ходной величины ко входной, преобразованных по Лапласу при нулевых на-

чальных условиях.

2.1.2. 3. Свойства и особенности передаточной функции

Передаточная функция устанавливает связь между входной и вы-

ходной величинами как в динамическом, так и в статическом

режимах.

Передаточная функция является функцией комплексной переменной

β+α= js

, которая может при некоторых значениях

обращаться

в нуль или в бесконечность. Значение переменной

, при котором

0)( =sW

, называется нулем, а значение, при котором

∞

)(sW

полюсом передаточной функции. Из (2.7) следует, что нулями явля-

ются корни полинома

)(sB

, а полюсами – корни полинома

)(sA

3. Корни полиномов

)(sB

)(sA

могут быть комплексными сопря-

женными и вещественными. Если эти корни известны, то в соответ-

ствии с теоремой Безу выражение (2.7) можно представить в виде:

01 2

(- )(- ) (- )

()

(- )(- ) (- )

bs s s

as s s

ρρ

λλ

…

где

- нули, а

- полюса

)(sW

4. Если полином

)(sA

имеет один или несколько нулевых корней, то

передаточную функцию можно представить в форме с явным выде-

лением этих корней, а именно, в виде:

()

Ws k

, (2.8)

где:

- коэффициент передачи по соответствующему каналу;

1)(lim

→

;

- количество нулевых корней полинома

)(sA

В самом деле передаточная функция (2.7) имеет полюса, когда один

или несколько младших коэффициентов полинома

)(sA

равны нулю:

nn nr

aa a

−−+

=== =K

, т.е.

()

nn r

bs bs b

as as a s

−

+++

, или

после преобразований:

() ()

rrnrnr

Bs Bs

Ws W s

ssAsAs

−

−−−

где

mii

bbB =

при

mi ,0=

;

jnr

Aaa

−

при

0,jnr

−

;

mnr

kba

−

Элементы САУ, у которых

0r >

, называются астатическими, т.е. не

имеющими статического режима, характеризуемого однозначной зависимо-

стью между входной и выходной величинами. Величину

при этом принято

называть порядком астатизма. Если же

, то элемент называется статиче-

ским.

Для проверки приведенного утверждения воспользуемся теоре-

мой о конечном значении оригинала операционного исчисления и формулой

(2.8) при условии

)( xconsttx

Имеем: