Зырянов Г.В. Системы управления многосвязными объектами

Подождите немного. Документ загружается.

Анализируя пути прохождения сигналов в этой схеме, легко заметить, что

связь выхода МДЗ y(t) с его входом u(t) при нулевых начальных условиях, будет

определяться только наличием и свойствами части "II" (полностью управляемой и

наблюдаемой) в составе ММ МДЗ. Поэтому, не проводя сложных математиче-

ских преобразований, можно записать следующее выражение для передаточной

матрицы МДЗ:

).()(

]

[

)(

222

pppp WDBAEСDBAECW =+−=+−=

−

(2.33)

Здесь W

(p) – передаточная матрица невырожденной (полностью управляемой и

наблюдаемой) части ММ МДЗ. Равенство

=)(

)(

становится возможным

только в результате алгебраических сокращений одинаковых сомножителей в

числителях и знаменателях дробно-рациональных выражений.

Отсюда следует важный вывод: Передаточная матрица МДЗ и все другие ха-

рактеристики вход-выход (весовая и переходная матрицы, частотные характери-

стики) полностью характеризуют свойства только управляемой и наблюдаемой

(невырожденной) части ММ МДЗ. Очевидно и то, что несокращаемые полюсы

передаточной матрицы – это собственные значения только матрицы A

и они, в

общем случае, не исчерпывают всех характеристических корней МДЗ, поскольку

составляют лишь часть от общего набора собственных значений матрицы

Полное их совпадение будет лишь при отсутствии неуправляемых и ненаблюдае-

мых частей. В то же время сокращаемые полюсы будут собственными значениями

матриц A

, A

и это становится очевидным, если записать характеристиче-

ское уравнение для МДЗ с учетом блочного представления матрицы

)(

444333222111

=−−−−=−= AEAEAEAEAE ppppppH

(2.34)

Поэтому при исследовании устойчивости МДЗ по его передаточной матрице

необходимо убедиться в отсутствии неуправляемой и ненаблюдаемой частей, ли-

бо быть уверенным в том, что эти части устойчивы и им соответствуют устойчи-

вые характеристические корни, т.е. собственные значения матриц A

, A

Для исследования свойств управляемости и наблюдаемости МДЗ необязатель-

но приводить его ММ к указанной выше специальной форме (2.32) изменением

базиса пространства состояний. Эти свойства линейной динамической системы

(в нашем случае МДЗ) можно исследовать с помощью алгебраических критериев

Калмана, зная матричные коэффициенты уравнений состояния МДЗ в любом ба-

зисе. Для этого рассматриваются две вспомогательные блочные матрицы:

а) матрица управляемости U = [B AB A

B … A

N–1

B];

б) матрица наблюдаемости V = [C

… (A

)

N–1

Критерий управляемости: Динамическая система (или МДЗ) N-го порядка яв-

ляется полностью управляемой, если ранг r

матрицы U равен N. В противном

случае система имеет неуправляемую часть, порядок которой равен N–r

Критерий наблюдаемости: Динамическая система (или МДЗ) N-го порядка

является полностью наблюдаемой, если ранг r

матрицы V равен N. В противном

случае система имеет ненаблюдаемую часть, порядок которой равен N–r

Кроме того, если каким-либо способом (см. (2.19), (2.31)) получен полный,

несокращенный вариант квадратной передаточной матрицы МДЗ W(p), то дос-

таточным условием его полной управляемости и наблюдаемости будет отсутст-

вие одинаковых нулей и полюсов у определителя этой матрицы.

2.4. Структурные преобразования для соединений МДЗ

В соответствии с методологией системного подхода любое МДЗ, в зависимо-

сти от задачи исследования, можно рассматривать либо как неделимый элемент в

составе более сложного соединения, либо представлять его составным элементом,

состоящим из нескольких, более простых компонентов.

Часто исходная (первоначальная) структурная схема МСАР имеет нестан-

дартный вид, который не соответствует условиям применения выбранного метода

анализа или синтеза. В подобных случаях возникает задача приведения исходной

структуры к некоторому желаемому (стандартному, каноническому) виду. Решить

ее можно аналитически, исключив в уравнениях, описывающих исходную струк-

туру, все «лишние», промежуточные переменные и оставляя только входы и вы-

ходы звеньев в составе требуемой структуры.

Другой способ основан на структурных преобразованиях, состоящих в мно-

гошаговой замене отдельных участков (фрагментов) структурных схем, «эквива-

лентными» многомерными звеньями.

Иногда целесообразно применение комбинаций этих двух способов. При

этом эквивалентность понимается только в алгебраическом смысле как совпаде-

ние (с точностью до тождественных преобразований) передаточных матриц для

двух (или более) структурных представлений. Но это, в общем случае, не гаран-

тирует динамической эквивалентности исходной и преобразованной структуры.

Ранее было установлено, что из равенства передаточных матриц следует только

эквивалентность полностью управляемых и наблюдаемых частей этих структур.

По этой причине указанные преобразования, связанные с алгебраической эквива-

лентностью передаточных матриц, должны применяться с известной осторожно-

стью и в строгом соответствии с рядом ограничительных рекомендаций. Наиболее

просто подобная задача эквивалентной замены решается для часто встречающих-

ся (типовых) соединений МДЗ.

2.4.1. Правила эквивалентной замены типовых соединений МДЗ

К типовым соединениям многомерных (многосвязных) динамических звеньев

МДЗ относятся следующие: а) последовательное; б) параллельное; в) встречно-

параллельное (с обратной связью). Получаемые для них выражения эквивалент-

ных передаточных матриц будут обобщением известных из теории одномерных

линейных систем управления формул (правил) структурных преобразований для

соединений звеньев, имеющих по одному входу и выходу.

а) Рассмотрим последовательное (каскадное) соединение N линейных МДЗ с

передаточными матрицами W

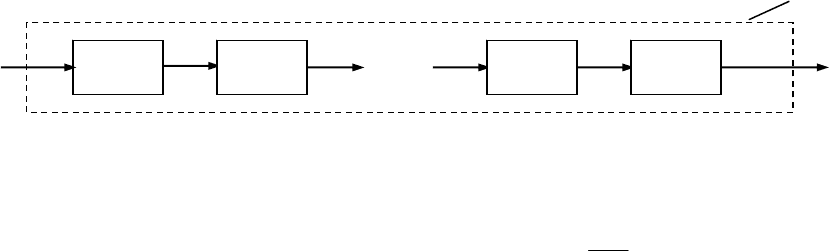
(p), Ni ,1= . Общий вид такого соединения пред-

ставлен на рис. 2.10. Здесь

(t) – вектор входа, а y

(t) – вектор выхода i-го звена.

Если размерности входа и выхода этого звена различны, то передаточная матрица

(p) будет прямоугольной, а иначе – квадратной. Особенностью этого соедине-

ния является то, что вход каждого последующего звена равен выходу предыду-

щего звена. При этом вход первого звена является входом, а выход последнего –

выходом для всего соединения.

(p) W

(p)

…

N–1

(p) W

(p)

f(p)

N–1

y(p)

N–1

W(p)=?

Рис. 2.10. Последовательное соединение МДЗ

Для этого соединения справедливы следующие математические соотношения

между изображениями Лапласа векторов входов и выходов:

(p) = W

(p)u

(p) при

Ni ,1=

;

(p) = y

i–1

(p) при N ≥ i > 1; (2.35)

(p) = y

(p); u

(p) = f(p).

Первое из этих выражений описывает свойства каждого из N МДЗ без учета

каких-либо взаимосвязей между ними. Второе – описывает взаимосвязи МДЗ

друг с другом, а третье – взаимодействие всего соединения с внешней средой.

Определим связь векторов

y(p) и f(p) путем последовательного исключения в

уравнениях (2.35) всех других (промежуточных) переменных. Тогда искомое вы-

ражение для

y(p) примет следующий вид:

y(p) = y

(p)=W

(p)u

(p) = W

(p)y

N–1

(p) = W

(p)W

N–1

(p)u

N–1

(p) =

(p)W

N–1

(p)W

N–2

(p)… W

(p)f(p) = W(p)f(p), (2.36)

где

W(p)= – передаточная матрица для последовательного соединения

МДЗ. Необходимо отметить, что порядок множителей в произведении, в отличие

от одномерного случая, не может быть произвольным, а должен быть строго об-

ратным направлению прохождения сигнала (даже для случая квадратных матриц).

∏

)(

Рассмотрим подробнее вопрос о наследовании свойств устойчивости, мини-

мальнофазовости, управляемости и наблюдаемости последовательного соедине-

ния МДЗ при замене его эквивалентным звеном.

Устойчивость и минимальнофазовость. Так как при перемножении переда-

точных матриц их нули и полюсы объединяются, то эквивалентное звено при от-

сутствии сокращений при получении W(p) будет устойчивым и минимальнофазо-

вым, если такими свойствами обладают все звенья в составе этого соединения.

Управляемость и наблюдаемость. Возможное совпадение нулей передаточ-

ных матриц одних звеньев с полюсами передаточных матриц других звеньев при

последовательном соединении обязательно приводит к появлению неуправляе-

мой, либо ненаблюдаемой частей в ММ эквивалентного звена. Сокращения мно-

жителей, соответствующих парам равных по значению нулей и полюсов, приво-

дит к понижению порядка ММ МДЗ и к динамической неэквивалентности.

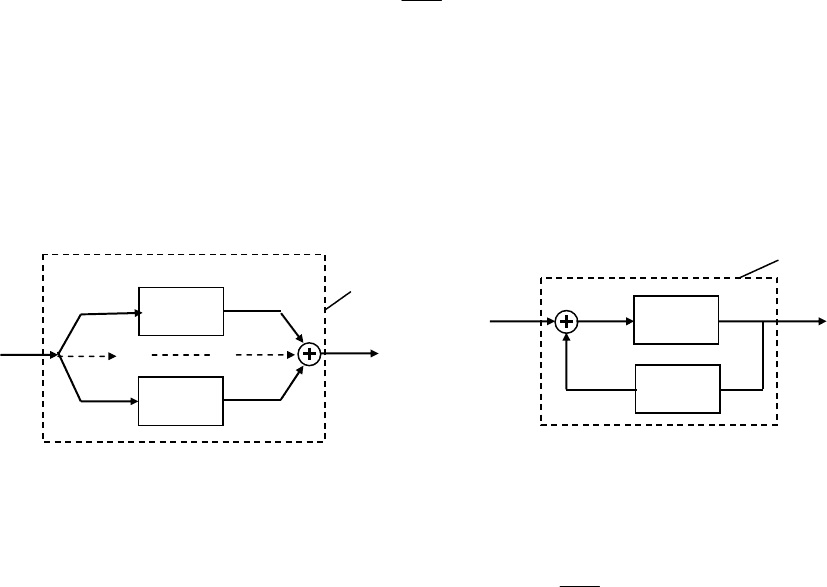
б) Рассмотрим параллельное соединение N линейных стационарных МДЗ с

передаточными матрицами W

(p),

Ni ,1=

. Общий вид такого соединения пред-

ставлен на рис. 2.11, а. Здесь, как и ранее, u

(t) – вектор входа, а y

(t) – вектор

выхода i-го звена. Особенностью этого соединения является то, что вектор входа

для каждого звена является одним и тем же (общим), а вектор выхода получается

алгебраическим суммированием выходов всех звеньев. Знак минус, в случае вы-

читания, относят к соответствующей передаточной матрице W

(p). При этом раз-

меры передаточных матриц для всех МДЗ должны быть одинаковыми.

W(p) = ?

(p)

f(p)

y(p)

(

)

(p)

б)

(p)

f(p)

(p)

y(p)

W(p) = ?

(p)

а)

Рис. 2.11. Параллельное и встречно-параллельное соединения МДЗ

Запишем следующие очевидные выражения относительно изображений Лап-

ласа векторов входов и выходов:

(p) = W

(p)u

(p) при Ni ,1= ; (2.37-а)

(p)=f(p); y(p) = . (2.37-б)

∑

)(y

Исключая в (2.37) промежуточные векторные переменные y

(p) и u

(p), по-

лучим зависимость выхода параллельного соединения y(p) от его входа f(p):

y(p) = = , (2.38)

∑

)(y

)()()()()()(

pppppp

fWfWuW =

∑

где W(p) = – передаточная матрица параллельного соединения МДЗ.

∑

)(W

Сохраняются ли свойства устойчивости, минимальнофазовости, управляемо-

сти и наблюдаемости для эквивалентного звена при параллельном соединении

многомерных динамических звеньев?

Устойчивость и минимальнофазовость. Так как при суммировании переда-

точных матриц их полюсы объединяются, то эквивалентное звено для параллель-

ного соединения будет устойчивым, если устойчивы все звенья в его составе. При

наличии хотя бы одного неустойчивого звена эквивалентное звено будет также

неустойчивым. Для нулей такого объединения нет и их нужно находить специ-

ально. Поэтому свойство минимальной фазы в общем случае не сохраняется.

Управляемость и наблюдаемость. Параллельное соединение управляемо и на-

блюдаемо, если таким свойством обладают все звенья в его составе. Исключением

является редкий, вырожденный случай, когда сумма двух (или более) слагаемых в

(2.38) равна нулю. При этом будет имеет место их параллельная компенсация.

в) Рассмотрим встречно-параллельное соединение двух МДЗ с передаточной

матрицей W

(p) в прямой цепи и W

(p) в цепи обратной связи (рис. 2.11, б). При

этом обратная связь может быть как положительной (верхний знак), так и отри-

цательной (нижний знак). Для получения "эквивалентной" передаточной матрицы

запишем следующие соотношения между обозначенными на схеме переменными:

y(p) = y

(p) = W

(p)ε(p); y

(p) = W

(p)y

(p); ε(p) = f(p) ± y

(p). (2.38)

Исключив в этих формулах векторные переменные ε(p), y

(p) и y

(p), получим

связь векторов выхода y(p) и входа f(p):

y(p) = y

(p) = W

(p)ε(p) = W

(p)(f(p) ± y

(p))= W

(p)(f(p) ± W

(p)y(p));

y(p)=[E W

(p)W

(p)]

–1

(p)f(p) = W(p)f(p); (2.39)

W(p) = [E W

(p)W

(p)]

–1

(p). (2.40)

Здесь W(p) – передаточная матрица для соединения с обратной связью. Если

(p) и W

(p) квадратные матрицы, то выражение для матрицы W(p) можно за-

писать разными способами в эквивалентном виде:

W(p) = [E W

(p)W

(p)]

–1

(p) = [W

–1

(p)

(p)]

–1

= W

(p)[E W

(p)W

(p)]

–1

. (2.41)

В этой формуле нижний знак «+» соответствует отрицательной, а верхний знак

«минус» − положительной обратной связи.

Вопрос об устойчивости, минимальнофазовости, управляемости и наблюдае-

мости решается следующим образом.

Устойчивость и минимальнофазовость. Из (2.41) следует, что полюсы со-

единения определяются сочетанием свойств прямого канала и цепи обратной свя-

зи, а нулями W(p) будут нули W

(p) и полюсы W

(p). Поэтому свойство устойчи-

вости, и минимальной фазы в общем случае не сохраняется.

Управляемость и наблюдаемость. Соединение будет управляемым и наблю-

даемым, если таким свойством будет обладать разомкнутый контур, т.е. последо-

вательное соединение МДЗ в прямом канале и в цепи обратной связи.

Часто для выявления типовых соединений в составе сложной структурной

схемы следует выполнить перенос точки съема сигнала (узла) или сумматора сиг-

налов через МДЗ. При этом передаточные матрицы между одноименными точка-

ми исходной и преобразованной структуры должны (с точностью до алгебраиче-

ских преобразований) совпадать. Это условие алгебраической (но не динамиче-

ской!) эквивалентности будет выполняться, если в переносимую цепь (ближе к

точке переноса) добавить МДЗ с передаточной матрицей, равной (или обратной)

передаточной матрице W(p) того звена, через которое осуществляется такой пе-

ренос. Причем в первом случае порядок ММ преобразованной схемы будет выше,

а во втором случае в составе ММ преобразованной схемы появятся неуправляе-

мые и/или ненаблюдаемые части. Более конкретно это определяется видом и на-

правлением переноса (табл. 2.2). Перенос узла в прямом направлении и сумматора

в обратном направлении возможен только в тех случаях, когда количество входов

и выходов МДЗ одинаково. При этом квадратная матрица W(p) не должна иметь

нулей в правой полуплоскости.

Таблица 2.2

Передаточная матрица МДЗ в переносимой цепи

Вид переноса →

Направление ↓

Узел Сумматор

Вперед

–1

(p) W(p)

W(p) W

–1

(p)

2.4.2. Передаточная матрица для произвольного соединения МДЗ

В общем случае исходная структурная схема для соединения линейных МДЗ

может содержать много звеньев и иметь сложную конфигурацию с различным со-

четанием прямых и обратных связей. Получение передаточной матрицы для тако-

го соединения путем поэтапного применения приведенных выше правил струк-

турных преобразований хотя и возможно, но оказывается слишком трудоемким

даже при использовании ЭВМ и современных математических пакетов. Более

конструктивным будет способ, основанный на идее унифицированного структур-

ного представления любой линейной системы с последующим применением пра-

вил замены типовых соединений МДЗ. При этом удается получить универсаль-

ную формулу для передаточной матрицы любого сложного соединения.

С этой целью рассмотрим произвольное соединение N линейных стационар-

ных МДЗ, каждое из которых имеет передаточную матрицу W

(p), вектор входов

(p) и вектор выходов y

(p) соответствующих размерностей. Пусть f(p) − вектор

входных воздействий для всего соединения (системы), а y

(p) − вектор его выхо-

да. Зависимости входов звеньев u

(p) от выходов y

(p) и от вектора входов со-

единения f(p) будем считать линейными и безынерционными. Аналогичное пред-

положение сделаем и для зависимости вектора выхода соединения y

(p).

Тогда для структурной схемы такого произвольного соединения, состоящего

из N МДЗ можно записать следующие выражения:

y*(p) = W*(p)u*(p); (2.42-а)

u*(p) = R

y*(p) + R

f(p); (2.42-б)

(p) = S

y*(p) + S

f(p). (2.42-в)

Здесь W*(p) – блочно-диагональная матрица; y*(p) и u*(p) – составные векторы,

определяемые следующим образом:

W*(p) = diag {W

(p)}; y*(p) = colon{u

(p)}; u*(p) = colon{y

(p)}, (2.43)

а R

, R

, S

– матричные коэффициенты безынерционных линейных зависи-

мостей между векторами входов и выходов.

Выражение (2.42-а) описывает в векторно-матричном виде свойства отдель-

ных МДЗ без учета их взаимосвязи, (2.42-б) описывает взаимодействие МДЗ меж-

ду собой и с внешней средой (по входам), а (2.42-в) – взаимодействие их с внеш-

ней средой по выходам.

Обобщенная структурная схема, построенная по этим выражениям, будет

иметь одинаковый (унифицированный) для любого соединения МДЗ, т.е. для всех

линейных динамических систем, вид:

W*(p)

f(p)

(p)

u*(p)

y*(p)

Рис. 2.12. Унифицированное структурное представление

для произвольного соединения МДЗ

Применяя к этой обобщенной структуре рассмотренные ранее правила эквива-

лентной замены типовых соединений многомерных звеньев, получим выражение

для передаточной матрицы произвольного соединения МДЗ:

Ф(p) = S

[E − W*(p)R

]

–1

W*(p)R

+ S

= S

{[W*(p)]

–1

− R

}

–1

+ S

. (2.44)

Эту формулу удобно использовать при компьютерных расчетах частотной пе-

редаточной матрицы Ф(jω). Из нее следует также, что полюсами Ф(p) будут нули

матрицы [E−W*(p)R

], называемой матрицей возвратных разностей. Далее бу-

дут рассмотрены и другие полезные применения этой формулы, например для

анализа устойчивости сложных линейных систем.

В структурном плане различные соединения будут отличаться между собой

только числом звеньев N и матрицами связей R

, R

, S

. Такую информацию

можно легко получить из структурной схемы в каждом конкретном случае, без

каких либо вычислительных действий. Эти матрицы являются клетками специ-

альной табличной формы записи (табл. 2.3) уравнений (2.42-б) и (2.42-в).

Таблица 2.3

u* R

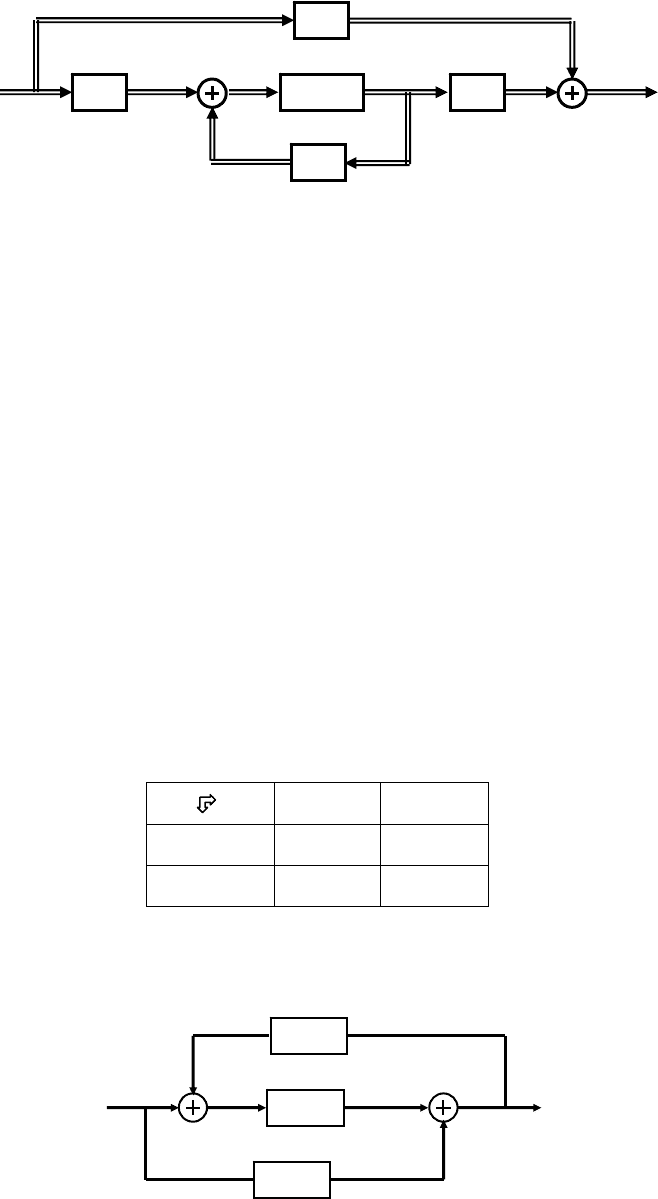
Для иллюстрации построения таблицы связей рассмотрим соединение трех

МДЗ с передаточными матрицами W

(p), W

(p), показанное на рис. 2.13.

(p)

f(p)

(p)

Рис. 2.13. Пример сложного соединения МДЗ

Таблица связей для этого соединения будет иметь вид (табл. 2.4).

Таблица 2.4

f y

0 0 E E

E E 0 0

E 0 0 0

0 0 E E

Тогда матрицы, необходимые для использования формулы (2.44) запишутся

следующим образом:

W*(p) = diag{W

(p), W

(p)};

⎥

⎦

⎤

⎢

⎣

⎡

000

00E

EE0

; R

= . S

⎥

⎦

⎤

⎢

⎣

⎡

= [0 E E]; S

= 0. (2.45)

2.4.3. Матрицы уравнений состояния для произвольного соединения МДЗ

Аналогичный подход можно применить для получения матриц A, B, C, D в

уравнениях состояния для произвольного соединения (с помощью безынерцион-

ных связей) N линейных физически осуществимых МДЗ с матричными коэффи-

циентами A

, BB

, C

, D

в уравнениях состояния каждого из них.

Для получения универсальных формул запишем сначала уравнения состояния

каждого МДЗ в каноническом виде без учета их взаимодействий:

.,1 ,

iiiii

=+=

uDxCy

uBxAx

Переходя к векторно-матричным обозначениям, получим уравнения

∗∗∗∗

∗∗∗

uDxCy

uBxAx

(2.46-a)

где x = colon{x

}; y* = colon{y

}; u* = colon{u

}– составные векторы; A*= diag{A

};

B* = diag{B

}; C* = diag{C

}; D* = diag{D

} – блочно-диагональные матрицы.

Уравнения безынерционных связей и взаимодействий учтем в виде выраже-

ний, аналогичных (2.42), но только во временной области:

u*(t) = R

y*(t) + R

f(t); (2.46-б)

(t) = S

y*(t) + S

f(t). (2.46-в)

Исключая в (2.46) промежуточные векторные переменные u*(t) и y*(t) пере-

пишем эти выражения в эквивалентном виде:

DfCxy

BfAxx

(2.47)

где матрицы A, B, C, D определяются следующими выражениями:

A = A* + B*[E – R

D*]

–1

C*;

B = B*[E – R

D*]

–1

;

C = S

[E – D*R

]

–1

C*; (2.48)

D = S

[E – D*R

]

–1

D*R

+ S

Эти универсальные формулы ориентированы на компьютерные вычисления с

помощью современных программных пакетов типа Mathcad. Они существенно

упрощаются, если для всех МДЗ в соединении отсутствует безынерционная связь

выхода с входом (D

=0). Тогда у всех элементов передаточных матриц порядки

числителей будут меньше порядков знаменателей и D* = 0. В этом случае для

всех типовых соединений преобразования (2.48) можно выполнить аналитически

и получить выражения для матриц A, B, C в конкретном виде.

А) последовательное соединение N многомерных звеньев (см. рис. 2.10):

⎥

⎦

⎤

⎢

⎣

⎡

; ;

⎥

⎦

⎤

⎢

⎣

⎡

0E00

0E0

00E

000

[

]

E00S K

; S

= 0.

⎥

⎦

⎤

⎢

⎣

⎡

− NNN

ACB00

0CB0

00ACB

000A

212

...

; ; C = [0 0 … C

⎥

⎦

⎤

⎢

⎣

⎡

Б) параллельное соединение N многомерных звеньев (см. рис. 2.11, а):

[

EEER K=

]

; R

=0;

[

]

EEES K

; S

= 0.

A = A* = diag{A

}; B=colon{BB

};

[

]

CCCC K

; D=0.

В) встречно-параллельное соединение многомерных звеньев (см. рис. 2.11, б):

⎥

⎦

⎤

⎢

⎣

⎡

;

⎥

⎦

⎤

⎢

⎣

⎡

; S

= 0;

[

]

0ES

;

⎥

⎦

⎤

⎢

⎣

⎡

212

211

ACB

CBA

; ;

⎥

⎦

⎤

⎢

⎣

⎡

[

]

0CC

; D = 0.

В этих формулах верхний знак соответствует положительной обратной связи.

Понятия управляемости и наблюдаемости естественно распространяются и на

произвольное соединение МДЗ. Для исследования этих свойств необходимо сна-

чала получить матрицы

A, B и C, а затем воспользоваться критериями Калмана.

2.5. Преобразования форм представления ММ МДЗ

При решении задач анализа и синтеза МСАР различные методы могут исполь-

зовать неодинаковые формы представления математических моделей (ММ) МДЗ.

В связи с этим возникает задача "эквивалентного" перехода от одной формы запи-

си ММ МДЗ к другой. Но в отличие от одномерного случая, эта задача не всегда

решается однозначно и просто, а иногда при этом возникают принципиальные

трудности. Поэтому есть смысл рассмотреть этот вопрос более подробно.

Обычно в теоретических исследованиях используют следующие три стандарт-

ные формы задания ММ МДЗ: I. Уравнение "вход-выход"; II. Уравнения состоя-

ния; III. Передаточная матрица.

Формально при этом возможны шесть видов задач перехода от одной формы

ММ МДЗ к другой (табл. 2.5).

Таблица 2.5

Формы записи ММ МДЗ и задачи перехода

Вид ММ МДЗ Форма записи Задача перехода

I. Уравнение

"вход-выход"

(D)y(t) = P(D)u(t)

1. "I

⇒ III" 4. "I ⇒ II"

II. Уравнения

состояния

).()(

),()(

DuCxy

BuAxx

2. "II

⇒ III" 5. "II ⇒ I"

III. Передаточная

матрица

(p)

3. "III

⇒ I" 6. "III ⇒ II"

Наиболее просто выполняются переходы от математического описания во

временной области к описанию МДЗ в комплексной области, т.е. задачи "I

⇒ III "

и "II

⇒ III". Решение этих задач было получено в п. 2.3:

W(p) = Q

–1

(p)P(p). (2.49)

W(p) = C[pE – A]

–1

B + D. (2.50)

Более сложными являются остальные задачи. Познакомимся с некоторыми из

них более детально.

♦Задача "I ⇒ II". Переход от уравнения "вход-выход" к уравнениям состояния

МДЗ. Эта задача не имеет единственного решения. Трудности связаны с неодно-

значностью выбора базиса в пространстве состояний, а также со структурными

особенностями МДЗ, с его управляемостью и наблюдаемостью.

Рассмотрим некоторые частные, но типовые варианты этой задачи. Пусть из-

вестно уравнение "вход-выход" n-мерного МДЗ в виде

Q(D)y(t) = P(D)f(t). (2.51)

Представим матрицы

Q(D) и P(D) в форме матричных полиномов:

Q(D) = ; P(D) = . (2.52)

∑

−

∑

−