Зубов В.Г., Шальнов В.П. Сборник задач по физике
Подождите немного. Документ загружается.

"
Ñîîòâåòñòâåííî, âíóòðè ìàëîé ñôåðû íàïðÿæåííîñòè
ïîëåé îáîèõ çàðÿäîâ E
1
= E
2
= 0, à ïîòåíöèàëû ïîñòîÿí-
íû è ðàâíû ϕ
1
=
11
/kq R
è ϕ
2
=
22
/kq R
. Ïîýòîìó
E = 0, ϕ = k
12
12
qq
RR
+
.
333. Òàê êàê ïî óñëîâèþ çàðÿä ðàñïðåäåëåí ñ îäèíàêî-
âîé ïëîòíîñòüþ σ ïî ïîâåðõíîñòè îáåèõ ñôåð, òî çàðÿä
âíóòðåííåé ñôåðû q
1
= 4πR
1
2
σ è âíåøíåé q
2
= 4πR
2
2
σ. Èñêî-
ìûé çàðÿä q = q
1
+ q
2
. Ðàáîòà A ïåðåíîñà çàðÿäà â öåíòð
ñôåð ðàâíà ïðîèçâåäåíèþ ïîòåíöèàëà ϕ ýòîãî öåíòðà íà
ïåðåíîñèìûé çàðÿä. Ïðè ýòîì (ñì. ðåøåíèå çàäà÷è 332)
A = ϕq
0
= k
12
12
qq
RR
+
q
0
, ãäå k =
0
1
4
πε
= 9·10
9
Í·ì
2
/Êë
2
,
q
0
= 1 Êë.
Ïîäñòàâëÿÿ çíà÷åíèÿ q
1
è q
2
, ïîëó÷èì
σ =
0
12
4()
q
kR R
ϕ
π+
.
Äëÿ q
1
, q
2
è q ïîëó÷èì ñîîòâåòñòâåííî
q
1
=
2
10
12
()
Rq
kR R
ϕ
+
, q
2
=
2
20
12
()
Rq
kR R
ϕ
+
, q =
22
120
12
()
()
RRq
kR R
ϕ+
+
;
q = 27,7 íÊë.
334. U
1
= Ed; U
1
= 1,5 êÂ; U
2
= E(d b); U
2
= 1,2 êÂ.
Ó ê à ç à í è å. Ïðè ââåäåíèè ìåòàëëè÷åñêîé ïëàñòè-
íû èñ÷åçàåò ýëåêòðè÷åñêîå ïîëå âî âñåì îáúåìå, çàíèìà-
åìîì ïëàñòèíîé. Ïðè ïåðåíîñå ïðîáíîãî çàðÿäà ñ îäíîé
ïëàñòèíû êîíäåíñàòîðà íà äðóãóþ ýëåêòðè÷åñêîå ïîëå
ñîâåðøàåò ðàáîòó òîëüêî íà ïóòè d b è â ñîîòâåòñòâèè
ñ ýòèì ïîñëå ââåäåíèÿ ìåòàëëè÷åñêîé ïëàñòèíû ïðîèçîé-
äåò óìåíüøåíèå ðàçíîñòè ïîòåíöèàëîâ ìåæäó ïëàñòèíà-
ìè êîíäåíñàòîðà äî çíà÷åíèÿ U
2
= E(d b).
335. Ëèñòî÷êè âñå âðåìÿ áóäóò ðàçâåäåíû íà îäèí è
òîò æå óãîë.
Ó ê à ç à í è å. Ïðè óêàçàííîì â óñëîâèè çàäà÷è
ñïîñîáå ïîäêëþ÷åíèÿ ýëåêòðîñêîïà åãî ïîêàçàíèÿ áóäóò
ïðîïîðöèîíàëüíû ïîòåíöèàëó ïîâåðõíîñòè òåëà. À òàê

"
êàê ïîòåíöèàëû âñåõ òî÷åê ïîâåðõíîñòè ïðî-
âîäíèêà â ýëåêòðîñòàòè÷åñêîì ïîëå îäèíà-
êîâû, òî è ðàñõîæäåíèå ëèñòî÷êîâ ýëåêò-
ðîñêîïà äëÿ âñåõ òî÷åê áóäåò îäèíàêîâî.
336. Ëèíèè íàïðÿæåííîñòè ïîëÿ ïðîõî-
äÿò âñþäó ïåðïåíäèêóëÿðíî ê ýêâèïîòåí-
öèàëüíûì ïîâåðõíîñòÿì è íàïðàâëåíû â ñòî-
ðîíó óáûâàíèÿ ïîòåíöèàëà (ðèñ. 279).
Íàïðÿæåííîñòü ïîëÿ áîëüøå òàì, ãäå ýêâèïîòåíöèàëü-
íûå ïîâåðõíîñòè ðàñïîëîæåíû áëèæå äðóã ê äðóãó.
337. Ðàáîòà ïðè ïåðåìåùåíèè çàðÿäà q íà ó÷àñòêàõ
NK è LM ðàâíà íóëþ, òàê êàê ñèëà
F
KH
= q
E
KH
ïåðïåíäè-
êóëÿðíà ê íàïðàâëåíèþ äâèæåíèÿ (ðèñ. 280). Ðàáîòû
ñèëû
F
KH
íà ó÷àñòêàõ MN è KL ðàâíû äðóã äðóãó ïî ìî-
äóëþ, íî ïðîòèâîïîëîæíû ïî çíàêó. Ñëåäîâàòåëüíî, ðà-
áîòà íà âñåì çàìêíóòîì êîíòóðå áóäåò ðàâíà íóëþ. Ýòîò
ðåçóëüòàò ñïðàâåäëèâ äëÿ âñåõ ýëåêòðîñòàòè÷åñêèõ ïî-
ëåé è çàìêíóòûõ êîíòóðîâ ëþáîé ïðîèçâîëüíîé ôîðìû.
338. Äëÿ äîêàçàòåëüñòâà ñëåäóåò ðàññ÷èòàòü ðàáîòó
ýëåêòðè÷åñêèõ ñèë ïðè ïåðåìåùåíèè çàðÿäà q ïî çàìê-
íóòîìó ïðÿìîóãîëüíîìó êîíòóðó MNKL (ðèñ. 281).
Òàê êàê ëèíèè íàïðÿæåííîñòè ïîëÿ ïàðàëëåëüíû, òî
íàïðÿæåííîñòü ïîëÿ
E
KH
âäîëü êàæäîé ëèíèè ïîñòîÿííà.
Ëèíèè íàïðÿæåííîñòè íà ó÷àñòêå MN ðàñïîëîæåíû ðåæå,
÷åì íà ó÷àñòêå KL, ïîýòîìó íàïðÿæåííîñòü ïîëÿ
E
KH
1
, à
çíà÷èò, è ðàáîòà À
1
ïåðåìåùåíèÿ çàðÿäà íà ó÷àñòêå MN
ïo ìîäóëþ çàâåäîìî ìåíüøå, ÷åì íàïðÿæåííîñòü
E
KH
2
è
ðàáîòà À
2
íà ó÷àñòêå KL. Ðàáîòà ïåðåìåùåíèÿ íà ó÷àñò-
1
2
Ðèñ. 279
Ðèñ. 280 Ðèñ. 281

"!
êàõ NK è LM ðàâíà íóëþ, òàê êàê âåêòîð
E
KH
ïåðïåíäèêóëÿðåí ê íàïðàâëåíèþ äâèæåíèÿ çà-
ðÿäà. Ñëåäîâàòåëüíî, ðàáîòà íà âñåì çàìêíóòîì
êîíòóðå MNKL, ðàâíàÿ A
1
À
2
, îòëè÷íà îò íóëÿ.
 ýëåêòðîñòàòè÷åñêîì ïîëå ðàáîòà ýëåê-
òðè÷åñêèõ ñèë íà ëþáîì çàìêíóòîì êîíòó-
ðå âñåãäà ðàâíà íóëþ (ñì. ðåøåíèå çàäà÷è
337), ò.å. ïîëó÷åííûé ðåçóëüòàò íåñîâìåñ-
òèì ñ îñíîâíûìè ñâîéñòâàìè ýëåêòðî-
ñòàòè÷åñêèõ ïîëåé è ñóùåñòâîâàíèå óêàçàí-
íîãî â óñëîâèè çàäà÷è ïîëÿ íåâîçìîæíî.
339. Äëÿ äîêàçàòåëüñòâà ñëåäóåò ðàññ÷èòàòü ðàáîòó ýëåê-
òðè÷åñêèõ ñèë íà çàìêíóòîì êîíòóðå MNKL (ðèñ. 282),
îãðàíè÷åííîì îòðåçêàìè ðàäèóñîâ NK è LM è äóãàìè
îêðóæíîñòåé MN è KL, ñîâïàäàþùèõ ñ ñîîòâåòñòâóþ-
ùèìè ëèíèÿìè íàïðÿæåííîñòè.
Èç ïàðàëëåëüíîñòè ëèíèé íàïðÿæåííîñòè ïîëÿ ñëå-
äóåò ïîñòîÿíñòâî íàïðÿæåííîñòè ïîëÿ
E
KH
1
íà ëèíèè MN
è
E
KH
2
íà ëèíèè KL. Ðàáîòà íà ó÷àñòêå MN ðàâíà E
1
Rα,
ðàáîòà íà ó÷àñòêå KL ðàâíà E
2
rα, ãäå R è r ðàññòîÿíèÿ
ëèíèé íàïðÿæåííîñòè ïîëÿ MN è KL îò òî÷êè Î. Íà
ó÷àñòêàõ NK è LM ðàáîòà ñèë ïîëÿ ðàâíà íóëþ (âåêòîð
E
KH
ïåðïåíäèêóëÿðåí ê íàïðàâëåíèþ äâèæåíèÿ çàðÿäà). Òàê
êàê â ýëåêòðîñòàòè÷åñêîì ïîëå ðàáîòà ýëåêòðè÷åñêèõ ñèë
íà çàìêíóòîì ïóòè âñåãäà ðàâíà íóëþ (ñì. ðåøåíèå çà-
äà÷ 337 è 338), òî äîëæíî áûòü
E
1
Rα E
2
rα = 0, èëè
1
2
E
E
=
r
R
,
÷òî è òðåáîâàëîñü äîêàçàòü.
§ 21. Ýëåêòðè÷åñêîå ïîëå â äèýëåêòðèêå
340. Ñêà÷êîîáðàçíîå èçìåíåíèå ÷èñëà ëèíèé íàïðÿæåí-
íîñòè ïîëÿ ïðè ïåðåõîäå ãðàíèöû äèýëåêòðèêà (ðèñ. 283)
îáúÿñíÿåòñÿ äåéñòâèåì ïîëÿðèçàöèîííûõ çàðÿäîâ, âîç-
Ðèñ. 282

""
íèêàþùèõ íà ãðàíèöå äèýëåêò-
ðèêà â ýëåêòðè÷åñêèõ ïîëÿõ.
341. E
1
=
2
1
kq
rε
; E
1
= 3 êÂ/ì;
E
2
=
2
2
kq
r
; E
2
= 2,25 êÂ/ì.
342. Åñëè áû âîêðóã øàðà íå
áûëî äèýëåêòðèêà, òî îí ñîçäàë
áû â îêðóæàþùåì ïðîñòðàíñòâå
ïîëå íàïðÿæåííîñòüþ E
1
=
2
kq
r
.
Ïðè íàëè÷èè æå äèýëåêòðèêà âîçíèêàåò ïîëå íàïðÿ-
æåííîñòüþ E
2
=
2
kq
r
ε
. Ðàçíîñòü ER = E
1
E
2
= k
2
1
q
r
ε−
ε
ðàâíà òîé íàïðÿæåííîñòè, êîòîðóþ ñîçäàþò ïîëÿðèçà-
öèîííûå çàðÿäû qR, âîçíèêøèå îêîëî çàðÿæåííîãî òåëà
(ðèñ. 284). Òàê êàê ýòè çàðÿäû ðàñïîëîæåíû òàêæå ðàâ-
íîìåðíî ïî ïîâåðõíîñòè ñôåðû, òî ìîæíî ïîëîæèòü
ER =
2
kq
r
′
. Ñîïîñòàâëÿÿ ïîëó÷åííûå âûðàæåíèÿ äëÿ ER,
íàéäåì, ÷òî
qR =
1
ε−
ε
q.
Ïîâåðõíîñòíàÿ ïëîòíîñòü
ïîëÿðèçàöèîííûõ çàðÿäîâ
σR =
2
4
q
R
′
π
=
1
ε−
ε
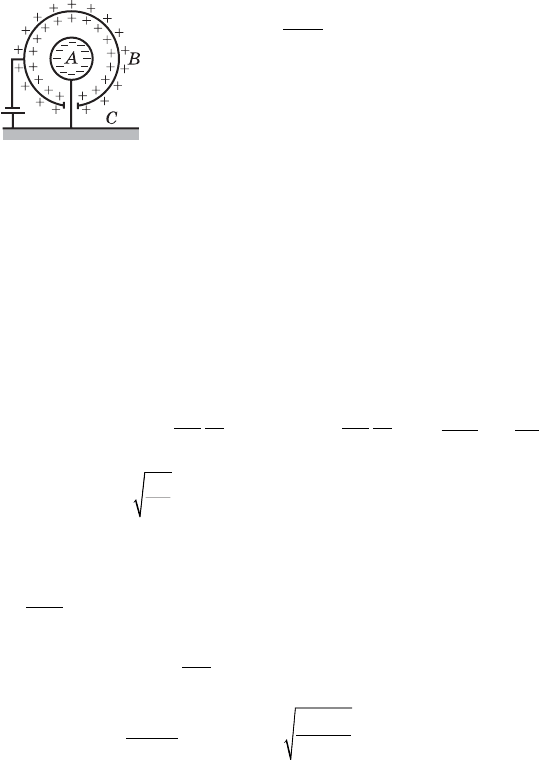
2
4
q
Rπ
=
=
1
ε−
ε
σ,
ãäå σ ïîâåðõíîñòíàÿ ïëîòíîñòü
ðàñïðåäåëåíèÿ çàðÿäà q íà øàðå.
343. Ïðè îïóñêàíèè øàðè-
êîâ â ìàñëî íà íèõ áóäóò äåé-
+
+
+
+
+
+
+
+
+
–
–
–
–
–
–
–
–
–
–
–
–
+
+
+
+
+
+
+
+
+
Ðèñ. 283
Ðèñ. 284

"#
ñòâîâàòü ñèëà òÿæåñòè m
g
H
è âûòàëêèâàþùàÿ ñèëà
A
F
KK H
0
A
mg
F
ρ
=
ρ
, êîòîðûå äàäóò ðàâíîäåéñòâóþùóþ, ìîäóëü
êîòîðîé ðàâåí
0
()
mg
ρ−ρ
ρ
. Ìîäóëü ñèëû ýëåêòðîñòàòè÷åñ-
êîãî âçàèìîäåéñòâèÿ çàðÿäîâ øàðèêîâ ðàâåí
2
2
kq
b
ε
. Óñëî-
âèå ðàâíîâåñèÿ øàðèêîâ çàïèøåòñÿ â âèäå
0
mg
ρ−ρ
ρ
tg α = k
2
2
q
bε
. (1)
Çàìå÷àÿ, ÷òî tg α =
2
b
l
, a l =
3
2
2
mga
kq
(ñì. ðåøåíèå çàäà÷è
304), è ïîäñòàâëÿÿ ýòè çíà÷åíèÿ â óðàâíåíèå (1), ïîëó÷èì
b = a
3
0
()
ρ
ερ−ρ
.
§ 22. Ýëåêòðè÷åñêàÿ åìêîñòü.
Êîíäåíñàòîðû
344. à) q
1
=
0
S
d
εε
1
; q
1
= 2,33 íÊë; á) q
2
=
0
S
d
ε
1
;
q
2
= 1,06 íÊë.
Óê à ç à í è å. à) Ïðè çàëèâàíèè ìàñëà çàðÿä íà ïëà-
ñòèíàõ âîçðàñòåò â ε ðàç çà ñ÷åò âîçðàñòàíèÿ åìêîñòè, íî
ðàçíîñòü ïîòåíöèàëîâ è íàïðÿæåííîñòü ïîëÿ îñòàíóòñÿ
íåèçìåííûìè; á) çàðÿä íà ïëàñòèíàõ ïðè çàëèâàíèè ìàñëà
îñòàíåòñÿ íåèçìåííûì, åìêîñòü êîíäåíñàòîðà âîçðàñòåò
â ε ðàç è â ñîîòâåòñòâèè ñ ýòèì â ε ðàç óìåíüøèòñÿ ðàç-
íîñòü ïîòåíöèàëîâ ìåæäó ïëàñòèíàìè è íàïðÿæåííîñòü
ïîëÿ â êîíäåíñàòîðå.
345. Åñëè îäíî èç òåë èìååò çàðÿä q, à äðóãîå òåëî â
ìåñòå ðàñïîëîæåíèÿ ïåðâîãî òåëà ñîçäàåò íàïðÿæåííîñòü
ïîëÿ E, òî íà ïåðâîå òåëî äåéñòâóåò ñèëà F = qE.
"$
Òàê êàê ïîòåíöèàëû ïðîâîäíèêîâ ïîääåðæèâàþòñÿ
ïîñòîÿííûìè, òî ïðè ïîìåùåíèè òåë â äèýëåêòðèê íà-
ïðÿæåííîñòü Å ïîëÿ, ñîçäàâàåìîãî êàæäûì èç òåë, âî
âñåõ òî÷êàõ äîëæíà îñòàòüñÿ òàêæå íåèçìåííîé. Ñ äðó-
ãîé ñòîðîíû, ïîìåùåíèå òåë â äèýëåêòðèê ïðèâåäåò ê
âîçðàñòàíèþ èõ ýëåêòðè÷åñêîé åìêîñòè â ε ðàç. Ïîýòîìó
äëÿ ñîõðàíåíèÿ ïîñòîÿíñòâà ïîòåíöèàëîâ íåîáõîäèìî
áóäåò óâåëè÷èòü çàðÿäû òåë òàêæå â ε ðàç.
Åñëè q çàðÿä ïåðâîãî òåëà â âîçäóõå, òî ïîñëå ïîìå-
ùåíèÿ òåë â äèýëåêòðèê çàðÿä ýòîãî òåëà äîëæåí ïðè-
íÿòü çíà÷åíèå εq è ñèëà âçàèìîäåéñòâèÿ òåë áóäåò
F
2
= εqÅ = εF
1
, ãäå F
1
= qE ñèëà, äåéñòâîâàâøàÿ íà òåëî
â âîçäóõå.
346. Åñëè çàðÿä q îñòàåòñÿ ïîñòîÿííûì, òî ïðè ñìåíå
äèýëåêòðèêîâ íàïðÿæåííîñòü ïîëÿ E áóäåò óìåíüøàòü-
ñÿ â ε ðàç, ò.å. ÅR =
E
ε
. Â ñîîòâåòñòâèè ñ ýòèì ñèëà, äåéñòâó-
þùàÿ íà êàæäûé èç øàðîâ è ðàâíàÿ F = qE, áóäåò óìåíü-
øàòüñÿ â ε ðàç. Åñëè îñòàþòñÿ ïîñòîÿííûìè ïîòåíöèàëû
øàðîâ, òî ñèëà, äåéñòâóþùàÿ íà êàæäûé èç øàðîâ, áóäåò
óâåëè÷èâàòüñÿ â ε ðàç (ñì. ðåøåíèå çàäà÷è 345).
347. Äëÿ ðåøåíèÿ çàäà÷è ñëåäóåò îïðåäåëèòü ïîòåí-
öèàëû êàæäîãî èç øàðîâ. Øàðû äîñòàòî÷íî óäàëåíû äðóã
îò äðóãà, ïîýòîìó ìîæíî ïîëîæèòü ϕ
1
=
1
1
kq
R
, ϕ
2
=
2
2
kq
R
.
Òàê êàê ϕ
1
> ϕ
2
, òî çàðÿäû áóäóò ïåðåìåùàòüñÿ êî âòîðî-
ìó øàðó. Ïåðåìåùåíèå çàðÿäîâ ïðåêðàòèòñÿ, êîãäà ïî-
òåíöèàëû øàðîâ âûðàâíÿþòñÿ. Ïðè ýòîì áóäóò èìåòü
ìåñòî ðàâåíñòâà
ϕR
1
= ϕR
2
=
1
1
kq
R
′
=
2
2
kq
R
′
, qR
1
+ qR
2
= q
1
+ q
2
.
Îòñþäà çàðÿä ïåðâîãî øàðà ïîñëå ñîåäèíåíèÿ
qR
1
=
1
12
R
RR
+
(q
1
+ q
2
),
è çàðÿä, ïåðåøåäøèé ñ ïåðâîãî øàðà íà âòîðîé,
q = q
1
qR
1
=
2
12
R
RR
+
q
1
1
12
R
RR+
q
2
; q d 6,67 íÊë.
"%
Ïîñëå ñîåäèíåíèÿ ïðîâîëîêîé øàðû áóäóò èìåòü çà-
ðÿäû qR
1
= 13,33 íÊë è qR
2
= 26,67 íÊë, à èõ îáùèé ïîòåí-
öèàë ϕ d 2,4 êÂ.
348. U =
11 22
12
CU CU
CC
+
+
= 260 Â.
Ó ê à ç à í è å. Äëÿ ðåøåíèÿ çàäà÷è ñëåäóåò îïðåäå-
ëèòü ñóììàðíûå çàðÿäû êîíäåíñàòîðîâ è åìêîñòü áàòà-
ðåè ïàðàëëåëüíî ñîåäèíåííûõ êîíäåíñàòîðîâ.
349. Çàðÿäû êîíäåíñàòîðîâ äî ñîåäèíåíèÿ ðàâíû
q
1
= C
1
U
1
è q
2
= C
2
U
2
. Çàðÿä, îñòàþùèéñÿ íà êîíäåíñàòî-
ðàõ ïîñëå ñîåäèíåíèÿ, ðàâåí Ñ
1
U
1
Ñ
2
U
2
. Åìêîñòü êîí-
äåíñàòîðîâ ïîñëå ñîåäèíåíèÿ ðàâíà C
1
+ Ñ
2
. Ðàçíîñòü ïî-
òåíöèàëîâ ìåæäó ïëàñòèíàìè êîíäåíñàòîðîâ ïîñëå ñî-
åäèíåíèÿ
U =
11 22
12
CU CU
CC
−
+
.
Çàðÿä, îñòàþùèéñÿ íà ïëàñòèíàõ ïåðâîãî êîíäåíñà-
òîðà ïîñëå ñîåäèíåíèÿ,
qR
1
= C
1
U = C
1
11 22
12
CU CU
CC
−
+
.
Çàðÿä, ïåðåøåäøèé ñ ïåðâîãî êîíäåíñàòîðà íà âòî-
ðîé, ðàâåí
q = q
1
qR
1
=
12 1 2
12
()
CC U U
CC
+
+
; q = 0,6 ìÊë.
350. ϕ = k
3
2
q
N
r
= 8,4 Â.
Ó ê à ç à í è å. Äëÿ ðåøåíèÿ ñëåäóåò âîñïîëüçîâàòüñÿ
ôîðìóëîé åìêîñòè øàðà è ðàññ÷èòàòü ðàäèóñ áîëüøîé
êàïëè.
351. Íåëüçÿ, êîíäåíñàòîðû áóäóò ïðîáèòû. Èç ðàâåí-
ñòâà çàðÿäîâ íà ïëàñòèíàõ êîíäåíñàòîðîâ ñëåäóåò, ÷òî
U
1
C
1
= U
2
Ñ
2
, U
2
Ñ
2
= U
3
Ñ
3
, U
1
+ U
2
+ U
3
= U.
Ðåøàÿ ýòó ñèñòåìó óðàâíåíèé, ïîëó÷èì U
1
= 6 êÂ,
U
2
= 3 ê è U
3
= 2 êÂ.
"&
352. Ñ =
0
S
db
εε
−
; C d 4,65 ïÔ. Ïðè ïå-
ðåìåùåíèè ìåòàëëè÷åñêîé ïëàñòèíû
åìêîñòü êîíäåíñàòîðà ìåíÿòüñÿ íå
áóäåò.
Ó ê à ç à í è å. Äëÿ ðåøåíèÿ çàäà÷è
êîíäåíñàòîð ñ âäâèíóòîé â íåãî ïëàñòèíîé
ñëåäóåò ðàññìàòðèâàòü êàê ñèñòåìó äâóõ
ïîñëåäîâàòåëüíî ñîåäèíåííûõ ïëîñêèõ êîíäåíñàòîðîâ.
353. Åìêîñòü áóäåò ðàçëè÷íà.  ïåðâîì ñëó÷àå çàðÿäû
íà áîëüøîé ñôåðå ðàñïîëàãàþòñÿ òîëüêî ñ âíóòðåííåé
ñòîðîíû. Âî âòîðîì ñëó÷àå îíè ðàñïîëàãàþòñÿ ñ îáåèõ
ñòîðîí (ðèñ. 285), è åìêîñòü âñåãî êîíäåíñàòîðà íóæíî
ðàññ÷èòûâàòü êàê åìêîñòü ñèñòåìû äâóõ ïàðàëëåëüíî ñî-
åäèíåííûõ êîíäåíñàòîðîâ ñ îáêëàäêàìè ÀÂ è ÂÑ, ò. å.
åìêîñòü áóäåò áîëüøå.
354. F = qE =
2
0
1
2
q
Sε
; A = Fd =
2
0
1
2
q
Sε
d =
2
2
CU
=
2
2
q
C
.
355. σ = ε
0
2
F
dC
; σ = 0,56 ìêÊë/ì
2
(ñì. ðåøåíèå çàäà-
֏ 354).
356. Ñèëà, äåéñòâóþùàÿ íà âåðõíþþ ïëàñòèíó, mg =
=
2
2
CU
d
(ñì. ðåøåíèå çàäà÷è 354). Åìêîñòü ïëîñêîãî
êîíäåíñàòîðà Ñ =
0
S
d
ε
; îòñþäà
mg =
2
0
2
2
SU
d
ε
, ò.å. U =
2
0
2
dmg
Sε
; U d 5,9 êÂ.
357.  ïåðâîì ñëó÷àå ïðè ðàçäâèãàíèè ïëàñòèí ðàç-
íîñòü ïîòåíöèàëîâ îñòàåòñÿ ïîñòîÿííîé, íî åìêîñòü, à
ñëåäîâàòåëüíî, è çàðÿä íà ïëàñòèíàõ óìåíüøàþòñÿ. Ýòî
âûçîâåò ïîñòåïåííîå óìåíüøåíèå ñèëû âçàèìîäåéñòâèÿ
ïëàñòèí. Âî âòîðîì ñëó÷àå çàðÿä íà ïëàñòèíàõ îñòàåòñÿ
ïîñòîÿííûì, ñèëà âçàèìîäåéñòâèÿ ïëàñòèí ñîõðàíèò íà-
÷àëüíîå çíà÷åíèå âî âñå âðåìÿ ðàçäâèãàíèÿ ïëàñòèí.
Ðèñ. 285
"'
Ïîýòîìó ïðè îäèíàêîâîì ïåðåìåùåíèè ïëàñòèí ðàáîòà
âî âòîðîì ñëó÷àå áóäåò áîëüøå.
358. ε = 3.
§ 23. Çàêîíû ïîñòîÿííîãî òîêà
359. R =
l
S
ρ
; R = 17 ìÎì.
360. Åäèíèöà ñîïðîòèâëåíèÿ ßêîáè ðàâíà 5,75 Îì.
361. ρ =
RS
l
; ρ = 0,1 ìêÎìì.
362. Ñîïðîòèâëåíèå ïðîâîäà ëåòîì íà 313 Îì áîëüøå.
Ó÷åò èçìåíåíèÿ äëèíû ïðîâîäà äàñò ïîïðàâêó, íå ïðå-
âûøàþùóþ 0,6 Îì.
363. Ñîïðîòèâëåíèå íèòè ëàìïî÷êè R =
2
U
N
=
l
S
ρ
.
Óäåëüíîå ñîïðîòèâëåíèå íàêàëåííîé íèòè ρ =
0
0
T
T
ρ
. Äëè-
íà íèòè
l =
RS
ρ
=
0
0
RST
Tρ
=
2
0
0
UST
NT
ρ
; l d 19 ñì.
364. I = 2 À, ò. å. â 10 ðàç áîëüøå, ÷åì ïðè íîðìàëü-
íîì ðåæèìå.
365. Åìêîñòü êîíäåíñàòîðà Ñ =
0
S
d
εε
. Ñîïðîòèâëåíèå
êîíäåíñàòîðà ïîñëå çàïîëíåíèÿ ýëåêòðîëèòîì R =
d
Sγ
;
åãî ïðîâîäèìîñòü
G =
1
R
=
S
d
γ
; îòñþäà C =
0
εε
γ
G.
Ïîëó÷åííîå âûðàæåíèå èìååò îáùèé õàðàêòåð, ñïðà-
âåäëèâî äëÿ êîíäåíñàòîðîâ ëþáîé ôîðìû è øèðîêî èñ-
ïîëüçóåòñÿ ïðè ýëåêòðîòåõíè÷åñêèõ ðàñ÷åòàõ.

#
366. Èç çàêîíîâ ýëåêòðîëèçà ñëåäóåò, ÷òî ìàññà âåùå-
ñòâà, âûäåëÿþùåãîñÿ íà îäíîì èç ýëåêòðîäîâ,
m =
1
M
Fn
Iτ,
ãäå F = 9,65·10
4
Êë/ìîëü ïîñòîÿííàÿ Ôàðàäåÿ, I ñèëà
òîêà, τ âðåìÿ, Ì ìîëÿðíàÿ ìàññà, n âàëåíòíîñòü
âåùåñòâà.
Îáúåì âûäåëèâøåãîñÿ ïðè ïðîõîæäåíèè òîêà êèñëî-
ðîäà íà îñíîâàíèè çàêîíà Àâîãàäðî ñîñòàâëÿåò ïðè äàâ-
ëåíèè 760 ìì ðò. ñò.
1
3
îáúåìà ãðåìó÷åãî ãàçà è ðàâåí
V = 13,72 ñì
3
. Ìàññà âûäåëèâøåãîñÿ êèñëîðîäà ò = 0,0196 ã.
Ñèëà òîêà, ñîîòâåòñòâóþùàÿ åäèíèöå ñèëû òîêà Ëåíöà,
I = F
Mn
Mτ
= 0,065 A.
367. Ñèëà òîêà ïðè âûêëþ÷åííîì ðåîñòàòå I
0
=
0
U
R
= 4 À.
Ñîïðîòèâëåíèå R
1
îïðåäåëÿåòñÿ èç óðàâíåíèÿ
R
1
+ R
0
=
0
U
II
−∆
, èëè R
1
=
0
U
II
−∆
R
0
= 10 Îì.
Ñîîòâåòñòâåííî,
R
2
=
0
2
U
II
−∆
(R
1
+ R
0
) = 20 Îì,
R
3
=
0
3
U
II
−∆
(R
2
+ R
1
+ R
0
) = 60 Îì.
368. Ãàëüâàíîìåòð ñëåäóåò âêëþ÷èòü â öåïü ïîñëåäî-
âàòåëüíî. Øêàëà ïðèáîðà: ×, 12, 6, 4, ... , 12/n ÌÎì.
Íàèìåíüøåå ñîïðîòèâëåíèå, êîòîðîå ìîæíî èçìåðèòü
ãàëüâàíîìåòðîì, ðàâíî 0,3 ÌÎì.
Ó ê à ç à í è å. Çíà÷åíèÿ ñîïðîòèâëåíèé R
k
, ñîîòâåò-
ñòâóþùèå îòäåëüíûì äåëåíèÿì øêàëû ãàëüâàíîìåòðà,
îïðåäåëÿþòñÿ ïî ôîðìóëå
R
k
=
0
U
ki
, ãäå k íîìåð äåëåíèÿ øêàëû.
