Живоглядов В.Г. Теория движения транспортных и пешеходных потоков
Подождите немного. Документ загружается.

от интенсивности движения при квадратно – контурном управлении. Ана-
лиз проводится на основе данных табл. 9.2 и рис. 9.13. По графику можно
предположить, что зависимость носит линейный характер, однако для пра-
вильного выбора вида аналитической зависимости выполняются промежу-
точные вычисления. На отрезке изменения переменной x, т.е. х
[1; 2,2] вы-
берем точки х
1
= 1 и х
n
= 2,2 наиболее удаленных друг от друга (крайние).
Вычисляем х
арм
, х
геом
, х
гарм
по формулам (2.265) и на графике геометрически
находятся соответствующие значения переменной у. По данным табл. 9.2 на-
ходятся у
арм
, у
геом
, у
гарм
, при этом используются формулы (2.266):
x
арм
=
1,6
y
арм
=
11,36082691
y*
1
=
11,36042
x
геом
=
1,48324
y
геом
=
11,36000992
y*
2
=
11,33374
x
гарм
=
1,375
y
гарм
=
11,35919299
y*
3
=
11,30929
Сравнивая числовые значения у*
1
, у*
2
, у*
3
с у
арм
, у
геом
, у
гарм
и оценивая
погрешности проведенных вычислений по формулам (2.267)-(2.273) получе-
ны следующие результаты:
ε
1
=|
y*
1
-y
арм
|=
0,000405
ε
5
=|
y*
2
-y
геом
|=
0,026268
ε
2
=|
y*
1
-y
геом
|=
0,000412
ε
6
=|
y*
3
-y
арм
|=
0,051536
ε
3
=|
y*
1
-y
гарм
|=
0,001229
ε
7
=|
y*
3
-y
гарм
|=
0,049902
ε
4
=|
y*
2
-y
арм
|=
0,027085
После этого выбирается минимальная погрешность ε из ε
i
, (i=1, 2,…7).
ε= min (ε
1
, ε
2
, ε
3
, ε
4
, ε
5
, ε
6
, ε
7
) =0,000405
Так как ε
совпадает с ε
1
, то в качестве аналитической зависимости хо-
рошим приближением может служить зависимость у=ах+b, с неизвестными
параметрами а и b. Для уточнения этих параметров используется МНК. Со-
гласно этому методу значения параметров функциональной зависимости а и
b следует выбрать так, чтобы сумма квадратов погрешностей была наимень-
шей (уравнение (2.273)), т.е. F(а, в) =
n
i
ii
baxfy
1
2
)),;((( будет минимальной,
где ε
i
= у
i
– f (x
i
; a, b) – i-я погрешность (i=1, 2,…7).
Необходимым условием существования минимума функции двух пе-
ременных является равенство нулю всех ее частных производных. Значения
861
параметров а и b найдем из системы уравнений (2.275). Система уравнений
(2.275) примет следующий вид:
n
i
i
n
i
i
n
i
ii
n
i
i
n
i
i
ynbxa
yxxbxa
11
111
2
)(
Далее, находятся значения а и b, путем решения системы матричным
методом, предварительно осуществив расчеты, приведенные в табл. 9.5
Таблица 9.5
Данные расчетов для МНК при исследовании зависимости Т
0
от интенсивности движения
i x
i
y
i
(x
i
)
2
x
i
y
i
1 1 11,22458 1 11,22458
2 1,15 11,25847 1,3225 12,94724
3 1,3 11,2924 1,69 14,68012
4 1,45 11,32639 2,1025 16,42326
5 1,6 11,36042 2,56 18,17668
6 1,75 11,39451 3,0625 19,94039
7 1,9 11,42865 3,61 21,71443
8 2,05 11,46283 4,2025 23,49881
9 2,2 11,49707 4,84 25,29356
∑
14,4 102,2453 24,39 163,8991
Итак, дана матрица коэффициентов при неизвестных вида:
L=
24,39
14,4
14,4
9
а также матрица свободных членов
M=
163,89906
102,24532
Используя X=L
-1
M, получим
Х=
0,227075225
10,9972704
где a= 0,227075225, b= 10,9972704, отсюда эмпирическая зависимость у=ах+
b при найденных значениях a и b принимает вид
y=0,2270752*x+10,9972704 .
Для определения точности выбора эмпирической кривой, т.е. макси-
мального отклонения табличных значений от аппроксимирующей прямой
y=0,195*x составим сравнительную табл. 9.6.
862
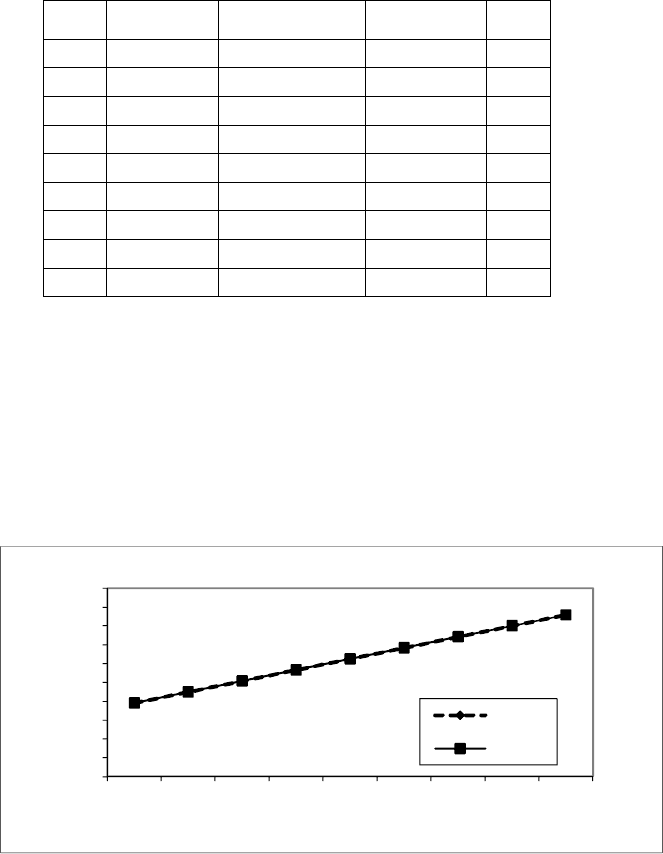
Таблица 9.6
Результаты отклонений табличных значений от значений, вычисленных по
эмпирической формуле y=0,2270752*x+10,9972704
x
i
y
i
y
i
выч
γ
i
%
1
11,22458
11,22434562
0,000236
0,00
1,15
11,25847
11,25840691
5,89*10
-
05
0,00
1,3
11,2924
11,29246819
6,78*10
-
05
0,00
1,45
11,32639
11,32652948
0,000144
0,00
1,6
11,36042
11,36059076
0,000169
0,00
1,75
11,39451
11,39465204
0,000143
0,00
1,9
11,42865
11,42871333
6,72*10
-
05
0,00
2,05
11,46283
11,46277461
5,92*10
-
05
0,00
2,2
11,49707
11,49683589
0,000236
0,00
Результаты отклонений табличных значений от вычисленных по эмпи-
рической формуле представлены на рис. 9.19.
Таким образом, размах отклонений значений табличных от вычислен-
ных 0,000236÷5,89*10
-05
, среднее взвешенное отклонение составляет 0,00 %,
что дает основание подтвердить точность выбранной эмпирической прямой.
0
0,05
0,1
0,15
0,2
0,25
0,3
0,35
0,4
0,45
0,5
1 1,15 1,3 1,45 1,6 1,75 1,9 2,05 2,2
Yi,Yiвыч
Xi
Yi
Yiвыч
Рис. 9.19. Результаты отклонений табличных значений от значений, вычисленных
по эмпирической формуле y=0,2270752*x+10,9972704
3. Изучение зависимости длительности цикла С от интенсивности
движения при квадратно – контурном управлении. Анализ проводится на ос-
нове данных табл. 9.2 и рис. 9.15. Для правильного выбора вида аналитиче-
ской зависимости выполняются промежуточные вычисления. На отрезке из-
менения переменной x, т.е. х
[1; 2,2] выберем точки х
1
= 1 и х
n
= 2,2 наиболее
удаленных друг от друга (крайние). Вычислим х
арм
, х
геом
, х
гарм
по формулам
(2.265) и на графике геометрически находятся соответствующие значения
переменной у. По данным табл. 9.2 находятся у
арм
, у
геом
, у
гарм
, при этом ис-
863
пользуются формулы (2.266).
x
арм
=
1,6
y
арм
=
54,02392
y*
1
=
32,87346
x
геом
=
1,48324
y
геом
=
41,9964
y*
2
=
27,08658
x
гарм
=
1,375
y
гарм
=
32,6466
y*
3
=
25,5083
Сравнивая числовые значения у*
1
, у*
2
, у*
3
с у
арм
, у
геом
, у
гарм
и оценивая
погрешности проведенных вычислений по формулам (2.267)-(2.273) получе-
ны следующие результаты:
ε
1
=|
y*
1
-y
арм
|=
21,15046
ε
5
=|
y*
2
-y
геом
|=
14,90982
ε
2
=|
y*
1
-y
геом
|=
9,122936
ε
6
=|
y*
3
-y
арм
|=
28,51562
ε
3
=|
y*
1
-y
гарм
|=
0,226861
ε
7
=|
y*
3
-y
гарм
|=
7,138302
ε
4
=|
y*
2
-y
арм
|=
2
6,93734
После этого выбирается минимальная погрешность ε из ε
i
, (i=1, 2,…7):
ε= min (ε
1
, ε
2
, ε
3
, ε
4
, ε
5
, ε
6
, ε
7
) =0,226861.
Так как ε совпадает с ε
3
, то в качестве аналитической зависимости хо-
рошим приближением служит зависимость у=1/(ах+b), с неизвестными пара-
метрами а и b. Для уточнения этих параметров используется МНК. Согласно
этому методу значения параметров функциональной зависимости а и b сле-
дует выбрать так, чтобы сумма квадратов погрешностей была наименьшей
(уравнение (2.274)), т.е. F(а, в) =
n
i
ii
baxfy
1
2
)),;((( будет минимальной,
где ε
i
= у
i
– f (x
i
; a, b) – i – я погрешность (i=1, 2,…7).
Необходимым условием существования минимума функции двух пе-
ременных является равенство нулю всех ее частных производных. Значения
параметров а и b найдем из системы уравнений (2.275). Поскольку зависи-
мость получилась нелинейная, то следует применять преобразование коор-
динат к функции у=1/(ах+b). Преобразовав у=1/(ах+b), получим 1/у=ах+в,
т.е. Z = A
1
t + B
1
, где Z =1/у; A
1
= a; B
1
= b; t = x.
Система уравнений (2.275) примет следующий вид (случай линейной
зависимости):
864
n
i
i
n
i
i
n
i
ii
n
i
i
n
i
i
znBtA
tztBtA
1
1
1
2
1
11
1
1
2
1
или
n
i
i
n
i
i
n
i
i
i
n
i
i
n
i
i
y
nbxa
y
x
xbxa
11
111
2
1
)(
Далее, находятся значения а и b, путем решения системы матричным
методом, предварительно осуществив расчеты, приведенные в табл. 9.7.
Таблица 9.7
Данные расчетов для МНК при исследовании зависимости длительности цикла С от
интенсивности движения при квадратно - контурном управлении
i x
i
y
i
1/y
i
x
i
2
x
i
y
i
1 1 20,0403 0,049899456 1 0,0498995
2 1,15 22,2275 0,044989317 1,3225 0,0517377
3 1,3 24,93388
0,04010608 1,69 0,0521379
4 1,45 28,36913
0,035249586 2,1025 0,0511119
5 1,6 32,87346
0,030419673 2,56 0,0486715
6 1,75 39,03782
0,025616182 3,0625 0,0448283
7 1,9 47,98705
0,020838955 3,61 0,039594
8 2,05 62,15877
0,016087834 4,2025 0,0329801
9 2,2 88,00755
0,011362662 4,84 0,0249979
∑
14,4 365,6355
0,274569746 24,39 0,3959587
Итак, дана матрица коэффициентов при неизвестных вида:
L=
24,39
14,4
14,4
9
а также матрица свободных членов
M=
0,3959587
0,2745697
Используя X=L
-1
M, получим
Х=
-0,032113253
0,081888955
где a= -0,032113253, b= 0,081888955, отсюда эмпирическая зависимость
у=1/(ах+b) при найденных значениях a и b принимает вид
y=1/(-0,0321133*x+0,0818890).
Для определения точности выбора эмпирической кривой, т.е. макси-
мального отклонения табличных значений от аппроксимирующей кривой
y=1/(-0,0321133*x+0,0818890), составим сравнительную табл. 9.8.
865
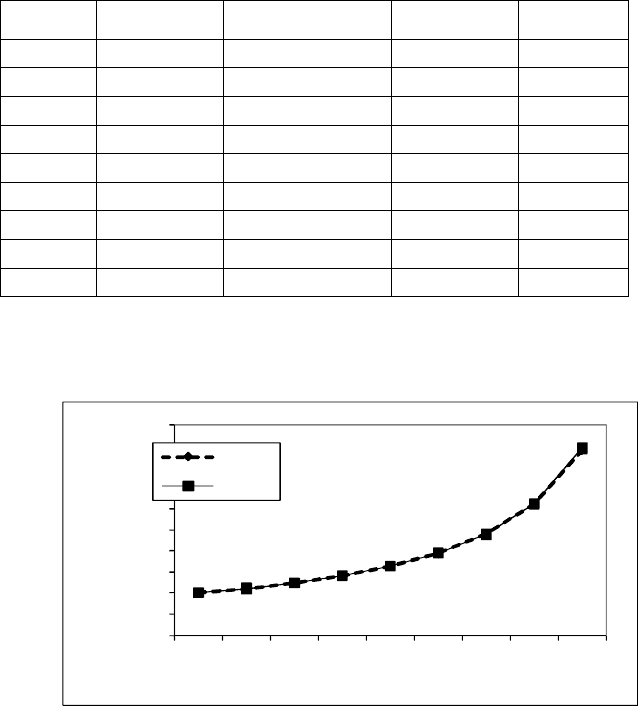
Таблица 9.8
Результаты отклонений табличных значений от значений, вычисленных по
эмпирической формуле y=1/(-0,0321133*x+0,0818890)
x
i
y
i
y
i
выч
γ
i
%
1
20,0403
20,09012366
0,049825
0,25
1,15
22,2275
22,2426293
0,01513
0,07
1,3
24,93388
24,91173426
0,022141
0,09
1,45
28,36913
28,30877365
0,060354
0,21
1,6
32,87346
32,77855675
0,094906
0,29
1,75
39,03782
38,92449814
0,113325
0,29
1,9
47,98705
47,90700629
0,080044
0,17
2,05
62,15877
62,27896601
0,120194
0,19
2,2
88,00755
88,96957428
0,962027
1,09
Результаты отклонений табличных значений от вычисленных по эмпи-
рической формуле представлены на рис. 9.20.
0
10
20
30
40
50
60
70
80
90
100
1 1,15 1,3 1,45 1,6 1,75 1,9 2,05 2,2
Yi,Yiвыч
Xi
Yi
Yiвыч
Рис. 9.20. Результаты отклонений табличных значений от значений, вычисленных
по эмпирической формуле y=1/(-0,0321133*x+0,0818890)
Таким образом, размах отклонений значений табличных от вычислен-
ных 0,015130,962027, среднее взвешенное отклонение составляет 0,00 ÷
0,03%, что дает основание подтвердить точность выбранной эмпирической
кривой.
4. Изучение зависимости длительности разрешающего сигнала t
зел
УДС
от интенсивности движения при квадратно – контурном управлении. Ана-
лиз проводится на основе данных табл. 9.2 и рис. 9.16. Для правильного вы-
бора вида аналитической зависимости выполняются промежуточные вычис-
ления. На отрезке изменения переменной x, т.е. х
[1; 2,2] выберем точки х
1
=
1 и х
n
= 2,2 наиболее удаленных друг от друга (крайние). Вычислим х
арм
, х
геом
,
х
гарм
по формулам (2.265) и на графике геометрически находятся соответст-
866
вующие значения переменной у. По данным табл. 9.2 определяем у
арм
, у
геом
,
у
гарм
, при этом используются формулы (2.266).
x
арм
=
1,6
y
арм
=
21,33
155
y*
1
=
10,75652
x
геом
=
1,48324
y
геом
=
12,98552
y*
2
=
7,876419
x
гарм
=
1,375
y
гарм
=
7,904896
y*
3
=
7,099504
Сравнивая числовые значения у*
1
, у*
2
, у*
3
с у
арм
, у
геом
, у
гарм
и оценивая
погрешности проведенных вычислений по формулам (2.267)-(2.273) получе-
ны следующие результаты:
ε
1
=|
y*
1
-y
арм
|=
10,57503
ε
5
=|
y*
2
-y
геом
|=
5,55*10
-
17
ε
2
=|
y*
1
-y
геом
|=
2,228997
ε
6
=|
y*
3
-y
арм
|=
0,022768
ε
3
=|
y*
1
-y
гарм
|=
2,851625
ε
7
=|
y*
3
-y
гарм
|=
0,043875
ε
4
=|
y*
2
-y
арм
|=
13,45513
После этого выбираем минимальную погрешность ε из ε
i
, (i=1, 2,…7):
ε= min (ε
1
, ε
2
, ε
3
, ε
4
, ε
5
, ε
6
, ε
7
) = 0,805391.
Так как ε
совпадает с ε
7
, то в качестве аналитической зависимости хо-
рошим приближением служит зависимость у=х/(ах+b), с неизвестными пара-
метрами а и b. Для уточнения этих параметров используется МНК. Согласно
этому методу значения параметров функциональной зависимости а и b сле-
дует выбрать так, чтобы сумма квадратов погрешностей была наименьшей
(уравнение (2.274)), т.е. F(а, в) =
n
i
ii
baxfy
1
2
)),;((( будет минимальной, где ε
i
= у
i
– f (x
i
; a, b) – i-я погрешность (i=1, 2,…7).
Необходимым условием существования минимума функции двух пе-
ременных является равенство нулю всех ее частных производных. Значения
параметров а и b найдем из системы уравнений (2.275):
0),(
0),(
baF
baF
b
a
или
.0)),;(((
0)),;(((
1
2
1
2
b
n
i
ii
a
n
i
ii
fbaxfy
fbaxfy
Поскольку зависимость получилась нелинейная, то следует применять
преобразование координат к функции у=х/(ах+b). Преобразовав у=х/(ах+b),
867
получим: 1/у=(ах+b)/х=a+b/x, т.е. Z = A
1
t + B
1
, где Z =1/у; A
1
= b; B
1
= a; t =
1/x.
Система уравнений (2.275) примет следующий вид (случай линейной
зависимости):
n
i
i
n
i
i
n
i
ii
n
i
i
n
i
i
znBtA
tztBtA
1
1
1
2
1
11
1
1
2
1
или
n
i
i
n
i
i
n
i
ii
n
i
i
n
i
i
y
naxb
yx
xaxb
11
111
2
1
/1
1
/1)/1(
Далее, находятся значения а и b, путем решения системы матричным
методом, предварительно осуществив расчеты, приведенные в табл. 9.9.
Таблица 9.9
Данные расчетов для МНК при исследовании зависимости длительности разре-
шающего такта t
зел
от интенсивности движения
при квадратно - контурном управлении
i x
i
y
i
1/y
i
1/x
i
(1/x
i
)
2
x
i
/y
i
1 1 4,407858
0,226867552
1 1 0,226867552
2 1,15 5,484517
0,182331472
0,869565
0,7561437
0,158549106
3 1,3 6,820737
0,146611715
0,769231
0,591716 0,112778242
4 1,45 8,521371
0,117352011
0,689655
0,4756243
0,080932421
5 1,6 10,75652
0,092966866
0,625 0,390625 0,058104292
6 1,75 13,82166
0,072350225
0,571429
0,3265306
0,041342985
7 1,9 18,2792 0,054706983
0,526316
0,2770083
0,028793149
8 2,05 25,34797
0,039450892
0,487805
0,2379536
0,019244338
9 2,2 38,25524
0,026140211
0,454545
0,2066116
0,011881914
∑
14,4 131,6951
0,958777927
5,993546
4,262213 0,738493999
Итак, дана матрица коэффициентов при неизвестных вида:
L=
4,262213
5,993546
5,993546
9
а также матрица свободных членов
M=
0,738494
0,9587779
Используя X=L
-1
M, получим
Х=
0,369243539
-0,139366684
где a= -0,139366684, b= 0,369243539, отсюда эмпирическая зависимость
у=х/(ах+b) при найденных значениях a и b принимает вид
y=x/(-0,1393667*x+0,3692435).
868
Для определения точности выбора эмпирической кривой, т.е. макси-
мального отклонения табличных значений от аппроксимирующей кривой
y=x/(-0,1393667*x+0,3692435) составим сравнительную табл. 9.10.
Таблица 9.10
Результаты отклонений табличных значений от значений, вычисленных по
эмпирической формуле y=x/(-0,1393667*x+0,3692435)
x
i
y
i
y
i
выч
γ
i
%
1
4,407858
4,350155214
0,057703
1,31
1,15
5,484517
5,503133489
0,018617
0,34
1,3
6,820737
6,91243566
0,091698
1,34
1,45
8,521371
8,674228138
0,152857
1,79
1,6
10,75652
10,93965894
0,183138
1,70
1,75
13,82166
13,96070428
0,139047
1,01
1,9
18,2792
18,1910722
0,08813
0,48
2,05
25,34797
24,53860334
0,809366
3,19
2,2
38,25524
35,12310322
3,132135
8,19
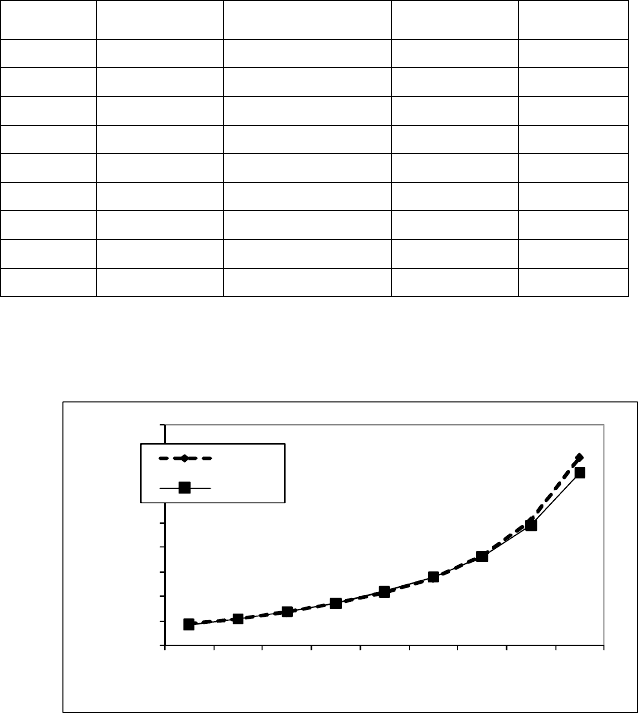
Результаты отклонений табличных значений от вычисленных по эмпи-
рической формуле представлены на рис. 9.21.
0
5
10
15
20
25
30
35
40
45
1 1,15 1,3 1,45 1,6 1,75 1,9 2,05 2,2
Yi,Yiвыч
Xi
Yi
Yiвыч
Рис. 9.21. Результаты отклонений табличных значений от значений, вычисленных
по эмпирической формуле y=x/(-0,1393667*x+0,3692435)
Таким образом, размах отклонений значений табличных от вычислен-
ных 0,088133,132135, среднее взвешенное отклонение составляет 0,34 ÷
8,19%, что дает основание подтвердить точность выбранной эмпирической
кривой.
5. Изучение зависимости максимальной пропускной способности j-го
направления УДС от интенсивности движения при квадратно – контурном
управлении. Анализ проводится на основе данных табл. 9.2 и рис. 9.17. По
графику можно предположить, что зависимость носит линейный характер,
869
однако для правильного выбора вида аналитической зависимости выполня-
ются промежуточные вычисления. На отрезке изменения переменной x, т.е. х
[1; 2,2] выберем точки х
1
= 1 и х
n
= 2,2 наиболее удаленных друг от друга
(крайние). Вычислим х
арм
, х
геом
, х
гарм
по формулам (2.265) и на графике гео-
метрически находятся соответствующие значения переменной у. По данным
табл. 9.2 определяем у
арм
, у
геом
, у
гарм
, при этом используются формулы (2.266):
x
арм
=
1,6
y
арм
=
1,963893
y*
1
=
1,963259
x
геом
=
1,48324
y
геом
=
1,855233
y*
2
=
1,837633
x
гарм
=
1,375
y
гарм
=
1,752585
y*
3
=
1,721622
Сравнивая числовые значения у*
1
, у*
2
, у*
3
с у
арм
, у
геом
, у
гарм
и оценивая
погрешности проведенных вычислений по формулам (2.266)-(2.272) получим
следующие результаты:
ε
1
=|
y*
1
-y
арм
|=
0,000634
ε
5
=|
y*
2
-y
геом
|=
0,0176
ε
2
=|
y*
1
-y
геом
|=
0,108026
ε
6
=|
y*
3
-y
арм
|=
0,242271
ε
3
=|
y*
1
-y
гарм
|=
0,210674
ε
7
=|
y*
3
-y
гарм
|=
0,030963
ε
4
=|
y*
2
-y
арм
|=
0,12626
После этого выбирается минимальная погрешность ε из ε
i
, (i=1, 2,…7):
ε= min (ε
1
, ε
2
, ε
3
, ε
4
, ε
5
, ε
6
, ε
7
) =0,000634
Так как ε
совпадает с ε
1
, то в качестве аналитической зависимости хо-
рошим приближением может служить зависимость у=ах+b с неизвестными
параметрами а и b. Для уточнения этих параметров используется МНК. Со-
гласно этому методу значения параметров функциональной зависимости а и
b следует выбрать так, чтобы сумма квадратов погрешностей была наимень-
шей (уравнение (2.274)), т.е. F(а, в) =
n
i
ii
baxfy
1
2
)),;((( будет минимальной,
где ε
i
= у
i
– f (x
i
; a, b) – i-я погрешность (i=1, 2,…7).
Необходимым условием существования минимума функции двух пе-
ременных является равенство нулю всех ее частных производных. Значения
параметров а и b найдем из системы уравнений (2.275). Система уравнений
(2.275) примет следующий вид:
870
