Живоглядов В.Г. Теория движения транспортных и пешеходных потоков

Подождите немного. Документ загружается.

геом

540

геом

2,751139

2,218

гарм

324

гарм

2,658039

2,1442

Сравнивая числовые значения у*1 , у*2 , у*3 с у

арм

, у

геом

, у

гарм

, и оце-

нивая погрешности проведенных вычислений по формулам (2.267)-(2.273)

получены следующие результаты:

-y

арм

0,4045

-y

геом

0,308139

-y

гарм

0,215039

-y

арм

0,6295

После этого выбирается минимальная погрешность ε из εi, (i=1,

2,…7):

ε= min (ε 1, ε 2 , ε 3 , ε 4, ε 5 , ε 6 , ε 7 ) =0,215039

Так как ε совпадает с ε

, то в качестве аналитической зависимости хо-

рошим приближением служит зависимость у=1/(ах+b), с неизвестными па-

раметрами а и b.

Для уточнения этих параметров используется метод наименьших

квадратов (МНК). Согласно этому методу значения параметров функцио-

нальной зависимости а и b следует выбрать так, чтобы сумма квадратов

погрешностей была наименьшей (уравнение (2.274)), т.е. F (а, в) =







baxfy

)),;((( будет минимальной, где ε

= у

– f (x

; a, b) – i-я погреш-

ность (i=1, 2,…7).

Необходимым условием существования минимума функции двух

переменных является равенство нулю всех ее частных производных.

Значения параметров а и b найдем из системы уравнений (2.275).

Поскольку зависимость получилась нелинейная, то следует приме-

нять преобразование координат к функции у=1/(ах+b).

Преобразовав у=1/(ах+b), получим: 1/у=ах+в, т.е. Z = A

t + B

, где Z

=1/у; A

= a; B

= b; t = x.

Система (2.274) примет следующий вид: (случай линейной зависимо-

сти):

-y

геом

0,533139

-y

арм

0,7033

-y

гарм

0,513839

701























znBtA

tztBtA

или























nbxa

xbxa

111

)(

Далее, находятся значения а и b, путем решения системы матричным

методом, предварительно осуществив расчеты, которые приведены в табл.

7.2

Таблица 7.2

Данные расчетов для МНК при определении зависимости длительности цикла от

интенсивности прибытия.

i x

1/y

1 180 2,113 0,473260767

32400 85,186938

2 360 2,152 0,464684015

129600 167,28625

3 540 2,218 0,450856628

291600 243,46258

4 720 2,313 0,432338954

518400 311,28405

5 900 2,443 0,409332788

810000 368,39951

6 1080

2,616 0,382262997

1166400

412,84404

7 1260

2,846 0,351370344

1587600

442,72663

8 1440

3,156 0,316856781

2073600

456,27376

9 1620

3,582 0,279173646

2624400

452,26131

∑

8100

23,439

3,560136918

9234000

2939,7251

Итак, дана матрица коэффициентов при неизвестных вида:

9234000

8100

а также матрица свободных членов

2939,7251

3,5601369

Используя X=L

-1

M, получим

Х=

0,000136007

0,517977328

где a= -0,000136007, b= 0,517977328,

Эмпирическая зависимость у=1/(ах+b) при найденных значениях a и b

принимает вид:

y=1/(-0,0001360*x+0,5179773).

Для определения точности выбора эмпирической кривой, т.е. макси-

мального отклонения табличных значений от аппроксимирующей кривой

y=1/(-0,0001360*x+0,5179773) составим сравнительную табл. 7.3.

Таблица 7.3

702

Результаты отклонений табличных значений от значений, вычисленных по эмпи-

рической формуле y=1/(-0,0001360*x+0,5179773)

выч

180 2,113

2,026358811

0,086641

4,10

360 2,152

2,132129315

0,019871

0,92

540 2,218

2,249549791

0,03155 1,42

720 2,313

2,380657176

0,067657

2,93

900 2,443

2,52799266 0,084993

3,48

1080

2,616

2,694768017

0,078768

3,01

1260

2,846

2,885102425

0,039102

1,37

1440

3,156

3,104367276

0,051633

1,64

1620

3,582

3,359701147

0,222299

6,21

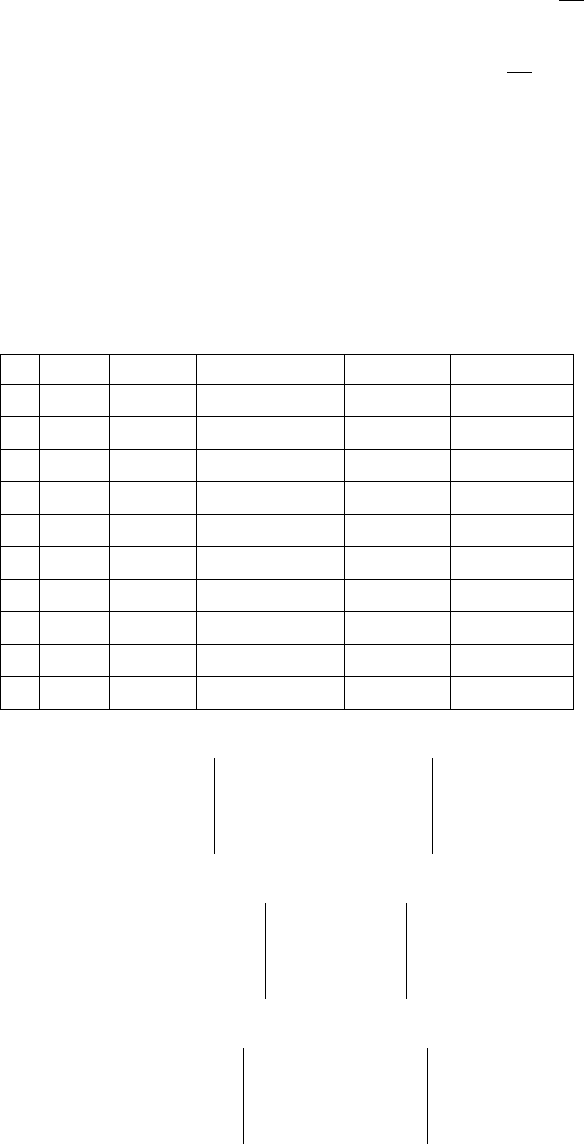
Результаты отклонений табличных значений от вычисленных по эм-

пирической формуле представлены на рис. 7.14.

0,5

1,5

2,5

3,5

180 360 540 720 900 1080 1260 1440 1620

Yi,Yiвыч

Yiвыч

Рис. 7.14. Результаты отклонений табличных значений от значений, вычисленных по

эмпирической формуле y=1/(-0,0001360*x+0,5179773)

Таким образом, размах отклонений значений табличных от вычис-

ленных 0,0198710,222299, среднее взвешенное отклонение составляет

0,92 ÷ 6,21%, что дает основание подтвердить точность выбранной эмпи-

рической кривой.

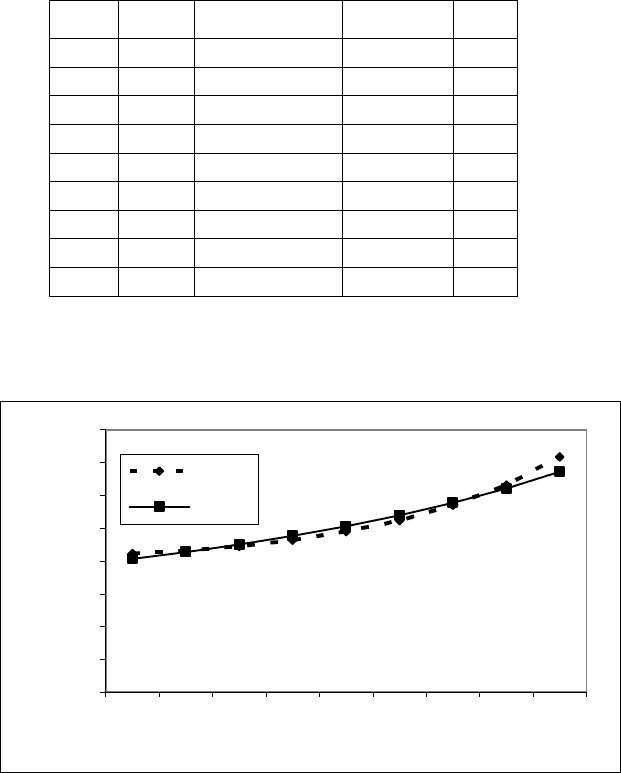
Для двухрядного движения зависимость y=1/(-

0,0002721*x+0,5598532), средне взвешенное отклонение составляет 1,91

31%, причем основное несовпадение графиков приходится на интенсив-

ность 1440- 1620 ТЕ/с (рис. 7.15).

703

180 360 540 720 900 1080 1260 1440 1620

Yi,Yiвыч

Yiвыч

Рис. 7.15. Результаты отклонений табличных значений от значений, вычисленных по

эмпирической формуле y=1/(-0,0002721*x+0,5598532) для двухрядного движения

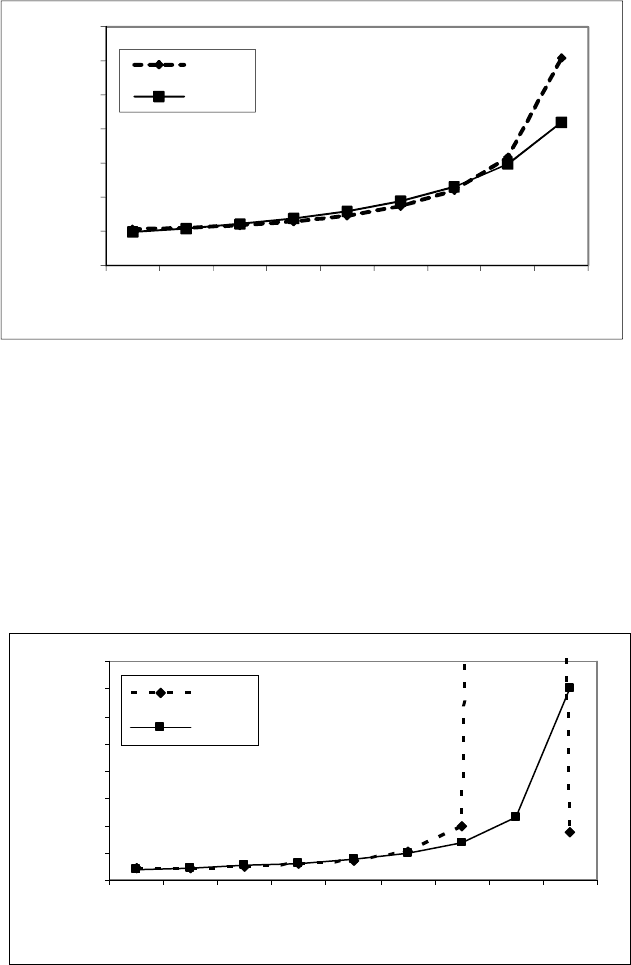
Для трехрядного движения зависимость y=1/(-0,0003220*x+0,5501065),

средне взвешенное отклонение составляет 1,73 303%, причем основное

несовпадение графиков приходится на интенсивность 1260 - 1620 ТЕ/с

(рис. 7.16).

180 360 540 720 900 1080 1260 1440 1620

Yi,Yiв ыч

Yiвыч

Рис. 7.16. Результаты отклонений табличных значений от значений, вычисленных по

эмпирической формуле y=1/(-0,0003220*x+0,5501065) для трехрядного движения

7.8.3. Изучение зависимости ширины проезжей части от скорости дви-

жения методом аппроксимированного моделирования

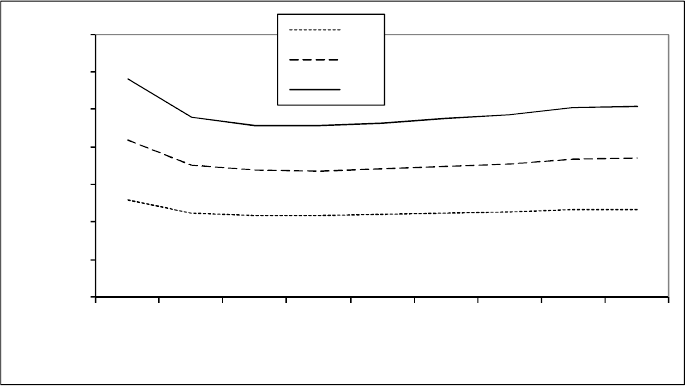
Анализ проведен на основе данных табл. 7.1 для интенсивности движе-

ния 180 ТЕ/ч (рис. 7.17).

704

1,99

2,01

2,02

2,03

2,04

2,05

2,06

15 30 45 60 75 90 105 120 135

Ширина проезжей части, м

Скорость движения, км/ч

Bn1

Bn2

Bn3

Рис. 7.17. Зависимость ширины проезжей части от скорости движения при интенсивно-

сти λ = 180 ТЕ/ч для одно-, двух- и трехрядного движения

Далее приведено подробное исследование для однорядного движе-

ния, для двух- и трехрядного последовательность действий та же, а резуль-

таты расчетов приведены ниже. Для правильного выбора вида аналитиче-

ской зависимости выполняются промежуточные вычисления. На отрезке

изменения переменной x, т.е. х



[15; 135] выберем точки х

= 15 и х

= 135

наиболее удаленных друг от друга (крайние). Вычисляем х

арм

, х

геом

, х

гарм

по

формулам (2.265) и на графике геометрически находятся соответствующие

значения переменной у. По данным табл. 7.1 определяем у

арм

, у

геом

, у

гарм

при этом используются формулы (2.264) и (2.266).

арм

2,013742

2,011978

геом

2,013741

2,011781

гарм

2,01374

2,013112

Сравнивая числовые значения y*

, y*

с у

арм

, у

геом

, у

гарм

, и оцени-

вая погрешности проведенных вычислений по формулам (2.267)-(2.273)

получены следующие результаты:

-y

арм

0,001764

-y

геом

0,001763

-y

гарм

0,001762

-y

арм

0,001961

После этого выбирается минимальная погрешность ε из ε

, (i=1,

2,…7):

ε= min (ε

, ε

) =0,000627

-y

геом

0,00196

-y

арм

0,0006

-y

гарм

0,000627

705

Так как ε совпадает с ε 7 , то в качестве аналитической зависимости

хорошим приближением служит зависимость у=х/(ах+b), с неизвестными

параметрами а и b. Для уточнения этих параметров используется МНК.

Согласно этому методу значения параметров функциональной зависимо-

сти а и b следует выбрать так, чтобы сумма квадратов погрешностей была

наименьшей (уравнение (2.274)), т.е. F(а, в) =







baxfy

)),;((( будет ми-

нимальной, где ε

= у

– f (x

; a, b) – i-я погрешность (i=1, 2,…7).

Необходимым условием существования минимума функции двух пе-

ременных является равенство нулю всех ее частных производных.

Значения параметров а и b найдем из системы уравнений (2.275):















0),(

baF

или



























.0)),;(((

0)),;(((

fbaxfy

Поскольку зависимость получилась нелинейная, то следует применять

преобразование координат к функции у=х/(ах+b). Преобразовав

у=х/(ах+b), получили: 1/у=(ах+b)/х=a+b/x, т.е. Z = A

t + B

, где Z =1/у; A

= b; B

= a; t = 1/x.

Система (2.275) примет следующий вид: (случай линейной зависимо-

сти):























znBtA

tztBtA

или























naxb

xaxb

111

/1)/1(

Далее, находятся значения а и b, путем решения системы матричным

методом, предварительно осуществив расчеты, которые приведены в табл.

7.4.

Таблица 7.4

Данные расчетов для МНК при определении зависимости ширины проезжей час-

ти от скорости движения

i x

1/y

1/x

(1/x

)

1/x

1 15 2,015735

0,496096976

0,066667

0,0044444

0,033073132

2 30 2,012457

0,496905104

0,033333

0,0011111

0,016563503

706

3 45 2,011781

0,497072 0,022222

0,0004938

0,011046044

4 60 2,011748

0,497080052

0,016667

0,0002778

0,008284668

5 75 2,011978

0,497023395

0,013333

0,0001778

0,006626979

6 90 2,012336

0,496934872

0,011111

0,0001235

0,005521499

7 105

2,012661

0,496854572

0,009524

9,07E-05 0,004731948

8 120

2,013247

0,496710026

0,008333

6,944E-05

0,00413925

9 135

2,013412

0,4966694 0,007407

5,487E-05

0,003679033

∑

675

18,11536

4,471346397

0,188598

0,0068434

0,093666055

Итак, дана матрица коэффициентов при неизвестных вида:

0,006843

0,188598

а также матрица свободных членов

0,0936661

4,4713464

Используя X=L-1M, получим

Х=

0,011220242

0,49705139

где a= 0,49705139, b= -0,011220242.

Эмпирическая зависимость у=х/(ах+b) при найденных значениях a и b

принимает вид

y=x/(0,4970514*x+-0,0112202).

Для определения точности выбора эмпирической кривой, т.е. макси-

мального отклонения табличных значений от аппроксимирующей кривой

y=x/(0,4970514*x+-0,0112202) составим сравнительную табл. 7.5.

Таблица 7.5

Результаты отклонений табличных значений от значений, вычисленных по

эмпирической формуле y=x/(0,4970514*x+-0,0112202)

выч

707

15 2,015735

2,014896639

0,000838 0,04

30 2,012457

2,013379381

0,000923 0,05

45 2,011781

2,012874136

0,001093 0,05

60 2,011748

2,012621609

0,000873 0,04

75 2,011978

2,012470123

0,000492 0,02

90 2,012336

2,012369145

3,3*10-05

0,00

105

2,012661

2,012297024

0,000364 0,02

120

2,013247

2,012242937

0,001004 0,05

135

2,013412

2,012200871

0,001211 0,06

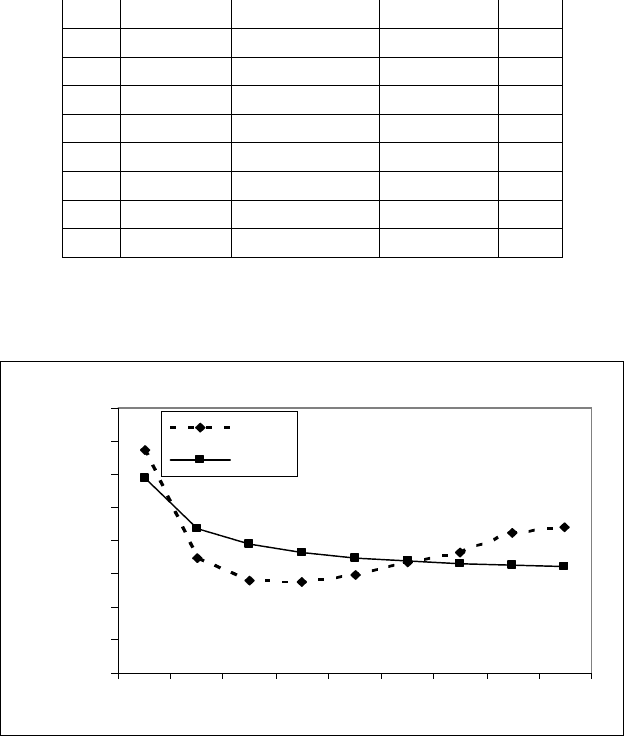
Результаты отклонений табличных значений от вычисленных по эм-

пирической формуле представлены на рис. 7.18.

2,009

2,01

2,011

2,012

2,013

2,014

2,015

2,016

2,017

180 360 540 720 900 1080 1260 1440 1620

Yi,Yiвыч

Yiвыч

Рис. 7.18. Результаты отклонений табличных значений от значений, вычисленных по

эмпирической формуле y=x/(0,4970514*x+-0,0112202)

Таким образом, размах отклонений значений табличных от вычислен-

ных 3,3*10

-05

0,001211, среднее взвешенное отклонение составляет 0,00 

0,06 %, что дает основание подтвердить точность выбранной эмпириче-

ской кривой.

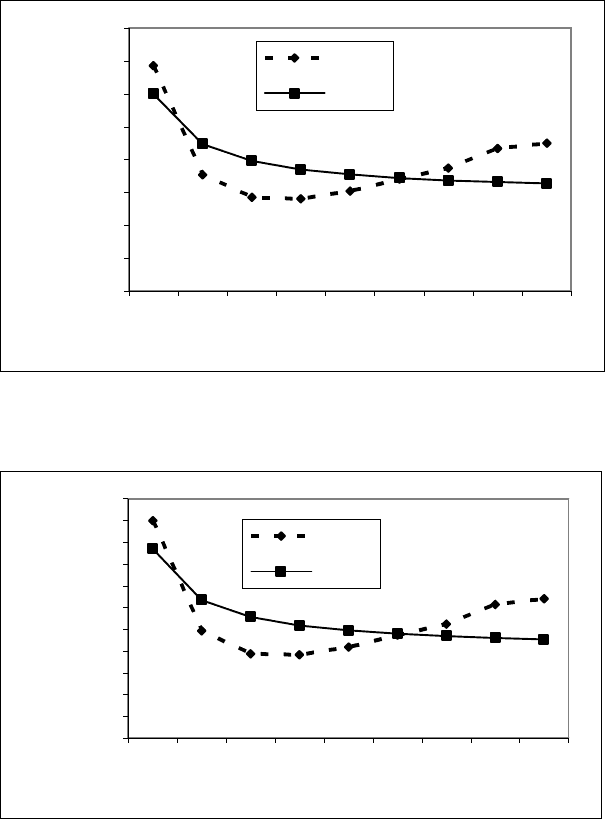
Для двухрядного движения (k=2) зависимость ширины проезжей час-

ти от скорости представлена уравнением y=x/(0,4941028*x+-0,0224405),

средне взвешенное отклонение составляет 0,00 0,12% (рис. 7.19).

708

2,018

2,02

2,022

2,024

2,026

2,028

2,03

2,032

2,034

15 30 45 60 75 90 105 120 135

Yi,Yiвыч

Yiвыч

Рис. 7.19. Результаты отклонений табличных значений от значений, вычисленных по

эмпирической формуле y=x/(0,4941028*x+-0,0224405) для двухрядного движения

2,028

2,03

2,032

2,034

2,036

2,038

2,04

2,042

2,044

2,046

2,048

2,05

15 30 45 60 75 90 105 120 135

Yi,Yiвыч

Yiвыч

Рис. 7.20. Результаты отклонений табличных значений от значений, вычисленных по

эмпирической формуле y=x/(0,4911542*x+-0,0336607) для трехрядного движения

Для трехрядного движения (k=3) зависимость представлена уравнени-

ем y=x/(0,4911542*x+-0,0336607), средне взвешенное отклонение составля-

ет 0,00 0,18% (рис. 7.20).

7.8.4. исследования полосы проезжей части на закруглениях дорог и

РКД

7.8.4.1 Блок – схема алгоритма расчета ширины проезжей части на за-

кругленных дорогах и РКД по формуле (7.6)

709

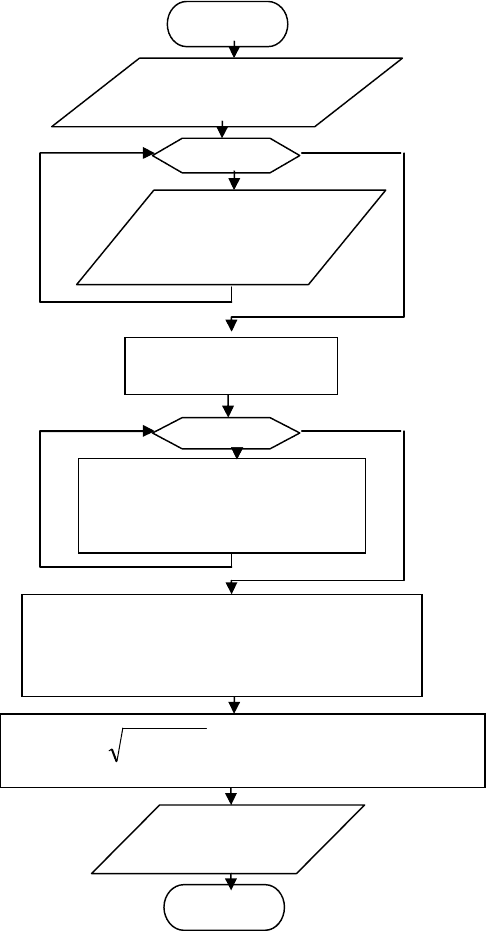
Комментарий к алгоритму

(1) - Начало алгоритма;

(2) - Ввод исходных данных

K, t

, t

, R

злк

, B

, j

уст

, l

;

(3) - Ввод исходных данных

по каждому из K рядов V

;

(4) - Обнуление сумм по q и

(5) - Подсчет q для каждого

ряда, суммарного значения q

для всех рядов и суммы ско-

ростей на всех рядах;

(6) -Подсчет среднего значе-

ния скорости и q для участка

магистрали, среднего дина-

мического габарита и вели-

чины h;

(7)-Подсчет ширины проез-

жей части B

;

(8)-Вывод значения B

;

(9)-Конец алгоритма.

7.8.4.2 Изучение зависимости ширины проезжей части на закругленных

дорогах и РКД от ширины проекции автомобиля на закруглениях методом

аппроксимированного моделирования

Для построения таблицы зависимости ширины проезжей части от

ширины проекции автомобиля на закруглениях, а точнее, от R

злк

и l

, взяты

следующие исходные данные: B

=2м, V=60км/ч, λ=180 ТЕ/ч, q=3, h=0,0048,

=40м, R

злк

= 0÷30 м, l

= 1÷10м. Данные расчета приведены в табл. 7.6.

Таблица 7.6

(1)

(2)

(3)

(5)

(8)

Начало

Ввод K, t

, t

, j

уст

, l

, R

злк

k:=1÷K

Ввод

, λ

k:=1÷K

:= λ

/ V

q:=q+ q

V:=V+ V

V:=V/K; q

:=q

:=(t

-t

)*V/3,6+V

/(26*j

уст

)+l

h:=1-e

-q

q:=0; V:=0

:=(B

азлк

lR  -R

злк

)/(1-0,001*L

*q*h)

Вывод

Конец

(4)

(6)

(7)

(9)

710