Живоглядов В.Г. Теория движения транспортных и пешеходных потоков
Подождите немного. Документ загружается.

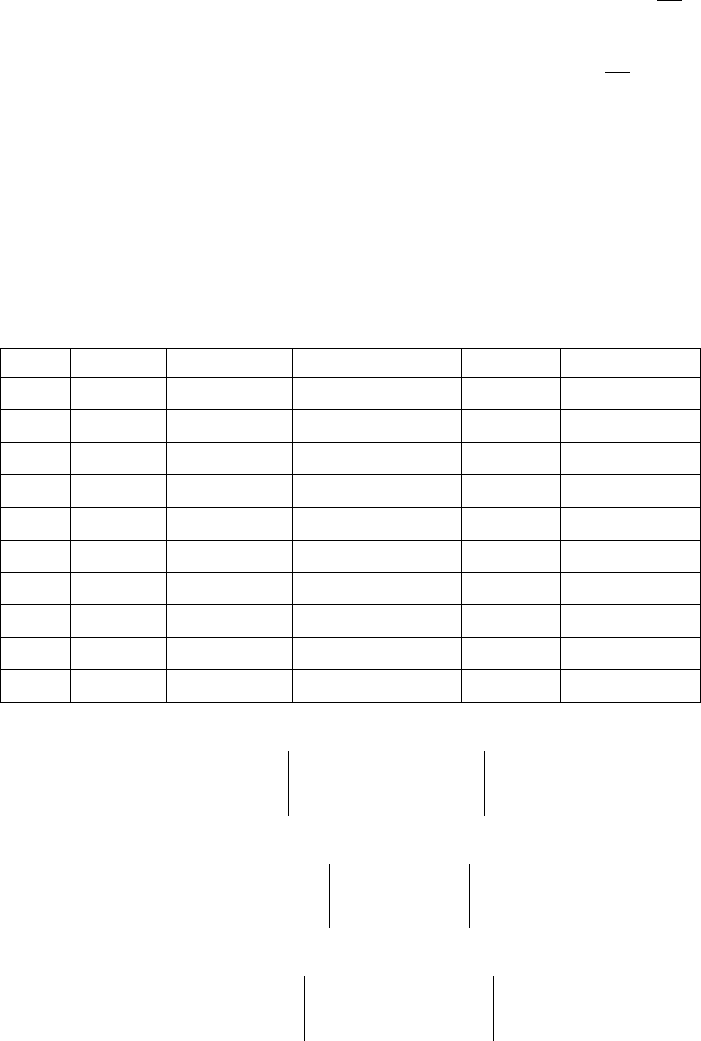
где Z =1/у; A
1
= a; B
1
= b; t = x.
Система уравнений (2.274) примет следующий вид: (случай линейной
зависимости):
n
i
i
n
i
i
n
i
ii
n
i
i
n
i
i
znBtA
tztBtA
1
1
1
2
1
11
1
1
2
1
или
n
i
i
n
i
i
n
i
i
i
n
i
i
n
i
i
y
nbxa
y
x
xbxa
11
111
2
1
)(
Далее, находятся значения а и b, путем решения системы матричным мето-
дом, предварительно осуществив расчеты, которые приведены в табл. 6.17.
Таблица 6.17.
Данные расчетов для МНК при исследовании зависимости k=tgα от интенсив-
ности движения
i
x
i
y
i
1/y
i
x
i
2
x
i
/y
i
1
0,1
2,055791
0,486430814
0,01
0,0486431
2
0,11
2,220291
0,450391456
0,0121
0,0495431
3
0,12
2,413559
0,414325933
0,0144
0,0497191
4
0,13
2,643863
0,378234353
0,0169
0,0491705
5
0,14
2,922978
0,342116826
0,0196
0,0478964
6
0,15
3,268257
0,305973461
0,0225
0,045896
7
0,16
3,706389
0,269804366
0,0256
0,0431687
8
0,17
4,280645
0,23360965
0,0289
0,0397136
9
0,18
5,066128
0,197389419
0,0324
0,0355301
∑
1,26
28,5779
3,078276279
0,1824
0,4092805
Итак, дана матрица коэффициентов при неизвестных вида:
L=
0,1824
1,26
1,26
9
а также матрица свободных членов
M=
0,4092805
3,0782763
Используя X=L
-1
M, получим
Х=
-3,613025041
0,847854203
где a= -3,613025041, b= 0,847854203, отсюда эмпирическая зависимость
у=1/(ах+b) при найденных значениях a и b принимает вид:
y=1/(-3,6130250*x+0,8478542).
661
Для определения точности выбора эмпирической кривой, т.е. макси-
мального отклонения табличных значений от аппроксимирующей кривой
y=1/(-3,6130250*x+0,8478542) составим сравнительную таблицу:
Таблица 6.18.
Результаты отклонений табличных значений от значений, вычисленных по
эмпирической формуле y=1/(-3,6130250*x+0,8478542)
x
i
y
i
y
i
выч
γ
i
%
0,1
2,055791
2,055280048
0,000511
0,02
0,11
2,220291
2,22014294
0,000148
0,01
0,12
2,413559
2,413761151
0,000202
0,01
0,13
2,643863
2,6443767
0,000513
0,02
0,14
2,922978
2,923714178
0,000736
0,03
0,15
3,268257
3,269037391
0,00078
0,02
0,16
3,706389
3,706858696
0,000469
0,01
0,17
4,280645
4,280090007
0,000555
0,01
0,18
5,066128
5,063042575
0,003085
0,06
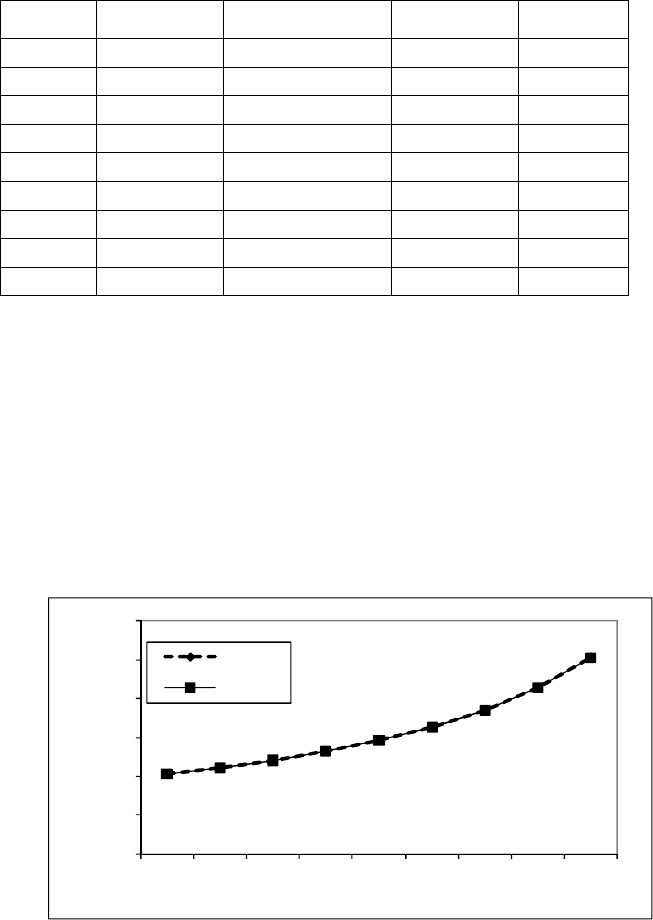
Результаты отклонений табличных значений от вычисленных по эмпи-
рической формуле представлены на рис. 6.37.
Таким образом, размах отклонений значений табличных от вычислен-
ных 0,0001480,000191, среднее взвешенное отклонение составляет 0,01 ÷
0,06%, что дает основание подтвердить точность выбранной эмпирической
кривой.
0
1
2
3
4
5
6
0,1 0,11 0,12 0,13 0,14 0,15 0,16 0,17 0,18
Yi,Yiвыч
Xi
Yi
Yiвыч
Рис. 6.37. Результаты отклонений табличных значений от значений, вычисленных
по эмпирической формуле y=1/(-3,6130250*x+0,8478542)
2. Изучение зависимости максимальной эффективности использования
разрешающего такта Н от интенсивности прибытия транспортных
средств к стоп-линии перекрестка.
662
Анализ проводится на основе данных табл. 6.16 и рис. 6.35. Для пра-
вильного выбора вида аналитической зависимости выполняются промежу-
точные вычисления. На отрезке изменения переменной x, т.е. х
[0,1; 0,18]
выберем точки х
1
= 0,1 и х
n
= 0,18 наиболее удаленных друг от друга (край-
ние). Вычисляем х
арм
, х
геом
, х
гарм
по формулам (2.265) и на графике геометри-
чески находятся соответствующие значения переменной у. По данным табл.
6.16 находим у
арм
, у
геом
, у
гарм
, при этом используем формулы (2.264) и (2.266):
x
арм
=
0,14
y
арм
=
0,930217
y*
1
=
0,947157
x
геом
=
0,134164
y
геом
=
0,928675
y*
2
=
0,952008
x
гарм
=
0,128571
y
гарм
=
0,927135
y*
3
=
0,939676
Сравнивая числовые значения у*
1
, у*
2
, у*
3
с у
арм
, у
геом
, у
гарм
и оцени-
вая погрешности проведенных вычислений по формулам (2.267)-(2.273) по-
лучены следующие результаты:
ε
1
=|
y*
1
-y
арм
|=
0,01694
ε
2
=|
y*
1
-y
геом
|=
0,018482
ε
3
=|
y*
1
-y
гарм
|=
0,020022
ε
4
=|
y*
2
-y
арм
|=
0,021791
После этого выбирается минимальная погрешность ε из εi, (i=1, 2,…7).
ε= min (ε
1
, ε
2
, ε
3
, ε
4
, ε
5
, ε
6
, ε
7
) =0,009459
Так как ε совпадает с ε
6
, то в качестве аналитической зависимости хо-
рошим приближением служит зависимость у=а+b/х, с неизвестными пара-
метрами а и b.
Для уточнения этих параметров используется МНК. Согласно этому
методу значения параметров функциональной зависимости а и b следует вы-
брать так, чтобы сумма квадратов погрешностей была наименьшей (уравне-
ние (2.273)), т.е. F(а, в) =
n
i
ii
baxfy
1
2
)),;((( будет минимальной, где ε
i
= у
i
– f
(x
i
; a, b) – i-я погрешность (i=1, 2,…7).
ε
5
=|
y*
2
-y
геом
|=
0,023333
ε
6
=|
y*
3
-y
арм
|=
0
,009459
ε
7
=|
y*
3
-y
гарм
|=
0,012541
663

Необходимым условием существования минимума функции двух пе-
ременных является равенство нулю всех ее частных производных. Значения
параметров а и b найдем из системы уравнений (2.275).
Поскольку зависимость получилась нелинейная, то следует применять
преобразование координат к функции у=а+b/х:
Преобразовав у=а+b/х, получим у=а+b/х, т.е. Z = A
1
t + B
1
, где Z =у; A
1
= b; B
1
= a; t = 1/x.
Система уравнений (2.274) примет следующий вид: (случай линейной
зависимости):
n
i
i
n
i
i
n
i
ii
n
i
i
n
i
i
znBtA
tztBtA
1
1
1
2
1
11
1
1
2
1
или
n
i
i
n
i
i
n
i
x
i
n
i
i
n
i
i
ynaxb
y
y
xaxb
11
111
2
/1)/1(
Далее, находятся значения а и b, путем решения системы матричным
методом, предварительно осуществив расчеты, которые приведены в табл.
6.19
Таблица 6.19
Данные расчетов для МНК при исследовании зависимости Н от
интенсивности движения
i x
i
y
i
1/y
i
x
i
2
x
i
/y
i
1 0,1 0,876675 10 100 8,7667536
2 0,11 0,898726 9,090909091 82,64463 8,1702338
3 0,12 0,91749 8,333333333 69,44444 7,6457517
4 0,13 0,933498 7,692307692 59,1716 7,1807519
5 0,14 0,947157 7,142857143 51,02041 6,7654089
6 0,15 0,958788 6,666666667 44,44444 6,3919194
7 0,16 0,96864 6,25 39,0625 6,0540031
8 0,17 0,976913 5,882352941 34,60208 5,7465442
9 0,18 0,983759 5,555555556 30,8642 5,4653281
∑ 1,26 8,461646 66,61398242 511,2543 62,186695
Итак, дана матрица коэффициентов при неизвестных вида:
L=
511,2543
66,61398
66,61398
9
а также матрица свободных членов
M=
62,186695
8,4616462
Используя X=L
-1
M, получим
664
Х=
-0,02431073
1,120120086
где a= 1,120120086, b= -0,02431073, отсюда эмпирическая зависимость
у=а+b/х при найденных значениях a и b принимает вид:
y=1,1201201+-0,0243107/x.
Для определения точности выбора эмпирической кривой, т.е. макси-
мального отклонения табличных значений от аппроксимирующей кривой
y=1,1201201+-0,0243107/x составим сравнительную табл. 6.20
Таблица 6.20
Результаты отклонений табличных значений от значений, вычисленных по
эмпирической формуле y=1,1201201+-0,0243107/x
x
i
y
i
y
i
выч
γ
i
%
0,1
0,876675
0,877012788
0,000337
0,04
0,11
0,898726
0,899113452
0,000388
0,04
0,12
0,91749
0,917530671
4,05*10
-
05
0,00
0,13
0,933498
0,933114472
0,000383
0,04
0,14
0,947157
0,946472016
0,000685
0,07
0,15
0,958788
0,958048554
0,000739
0,08
0,16
0,96864
0,968178025
0,000462
0,05
0,17
0,976913
0,977115793
0,000203
0,02
0,18
0,983759
0,985060476
0,001301
0,13
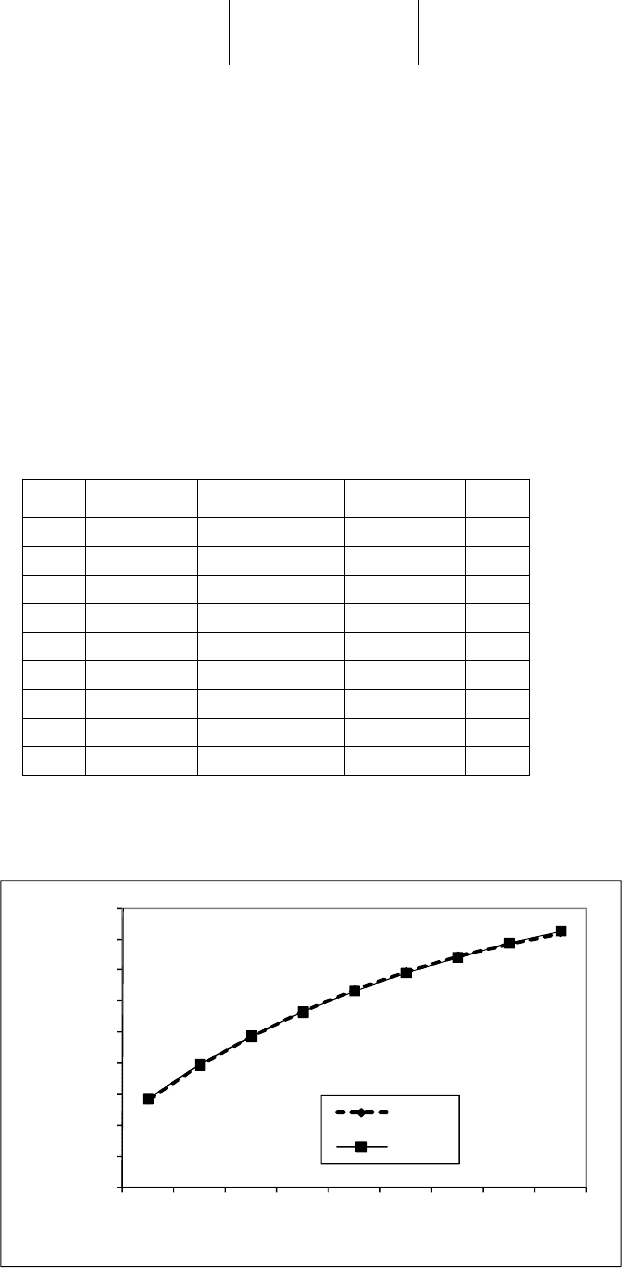
Результаты отклонений табличных значений от вычисленных по эмпи-
рической формуле представлены на рис. 6.38.
0,82
0,84
0,86
0,88
0,9
0,92
0,94
0,96
0,98
1
0,1 0,11 0,12 0,13 0,14 0,15 0,16 0,17 0,18
Yi,Yiвыч
Xi
Yi
Yiвыч
Рис. 6.38. Результаты отклонений табличных значений от значений, вычисленных
по эмпирической формуле y=1,1201201+-0,0243107/x
Таким образом, размах отклонений значений табличных от вычислен-
ных 4,05*10
-05
0,001301, среднее взвешенное отклонение составляет 0,00 ÷
665
0,13%, что дает основание подтвердить точность выбранной эмпирической
кривой.
3. Изучение зависимости отношения n
0j
/n
maxj
от интенсивности при-
бытия транспортных средств к стоп-линии перекрестка.
Анализ проводится на основе данных табл. 6.16 и рис. 6.36. Для пра-
вильного выбора вида аналитической зависимости выполняются промежу-
точные вычисления. На отрезке изменения переменной x, т.е. х
[0,1; 0,18]
выберем точки х
1
= 0,1 и х
n
= 0,18 наиболее удаленных друг от друга (край-
ние). Вычисляется х
арм
, х
геом
, х
гарм
по формулам (2.264) и на графике геомет-
рически находятся соответствующие значения переменной у. По данным
табл. (6.16) находятся у
арм
, у
геом
, у
гарм
, при этом используем формулы (2.264)
и (2.266):
x
арм
=
0,14
y
арм
=
0,930217
y*
1
=
0,
947157
x
геом
=
0,134164
y
геом
=
0,928675
y*
2
=
0,952008
x
гарм
=
0,128571
y
гарм
=
0,927135
y*
3
=
0,939676
Сравнивая числовые значения у*
1
, у*
2
, у*
3
с у
арм
, у
геом
, у
гарм
и оценивая
погрешности проведенных вычислений по формулам (2.267)-(2.273), полу-
чим следующие результаты:
ε
1
=|
y*
1
-y
арм
|=
0,01694
ε
2
=|
y*
1
-y
геом
|=
0,018482
ε
3
=|
y*
1
-y
гарм
|=
0,020022
ε
4
=|
y*
2
-y
арм
|=
0,021791
После этого выбирается минимальная погрешность ε из ε
i
, (i=1, 2,…7),
ε= min (ε
1
, ε
2
, ε
3
, ε
4
, ε
5
, ε
6
, ε
7
) =0,009459
Так как ε совпадает с ε
6
, то в качестве аналитической зависимости хо-
рошим приближением служит зависимость у=а+b/х, с неизвестными пара-
метрами а и b. Для уточнения этих параметров используется МНК. Согласно
этому методу значения параметров функциональной зависимости а и b сле-
дует выбрать так, чтобы сумма квадратов погрешностей была наименьшей
ε
5
=|
y*
2
-y
геом
|=
0,023333
ε
6
=|
y*
3
-y
арм
|=
0,009459
ε
7
=|
y*
3
-y
гарм
|=
0,012541
666

(уравнение (2.274)), т.е. F(а,в) =
n
i
ii
baxfy
1
2
)),;((( будет минимальной, где ε
i
=
у
i
– f (x
i
; a,b) – i-я погрешность (i=1, 2,…7). Необходимым условием сущест-
вования минимума функции двух переменных является равенство нулю всех
ее частных производных.
Значения параметров а и b найдем из системы уравнений (2.275). По-
скольку зависимость получилась нелинейная, то следует применять преобра-
зование координат к функции у=а+b/х:
Преобразовав у=а+b/х, получим у=а+b/х, т.е. Z = A
1
t + B
1
, где Z =у; A
1
= b; B
1
= a; t = 1/x.
Система уравнений (2.275) примет следующий вид: (случай линейной
зависимости):
n
i
i
n
i
i
n
i
ii
n
i
i
n
i
i
znBtA
tztBtA
1
1
1
2
1
11
1
1
2
1
или
n
i
i
n
i
i
n
i
x
i
n
i
i
n
i
i
ynaxb
y
y
xaxb
11
111
2
/1)/1(
Далее находим значения а и b путем решения системы матричным мето-
дом, предварительно осуществив расчеты, которые приведены в табл. 6.21
Таблица 6.21
Данные расчетов для МНК при исследовании зависимости отношения n
0j
/n
maxj
от интенсивности движения
i x
i
y
i
1/y
i
x
i
2
x
i
/y
i
1 0,1 0,876675 10 100 8,7667536
2 0,11 0,898726 9,090909091 82,64463 8,1702338
3 0,12 0,91749 8,333333333 69,44444 7,6457517
4 0,13 0,933498 7,692307692 59,1716 7,1807519
5 0,14 0,947157 7,142857143 51,02041 6,7654089
6 0,15 0,958788 6,666666667 44,44444 6,3919194
7 0,16 0,96864 6,25 39,0625 6,0540031
8 0,17 0,976913 5,882352941 34,60208 5,7465442
9 0,18 0,983759 5,555555556 30,8642 5,4653281
∑ 1,26 8,461646 66,61398242 511,2543 62,186695
Итак, дана матрица коэффициентов при неизвестных вида:
L=
511,2543
66,61398
66,61398
9
а также матрица свободных членов
667
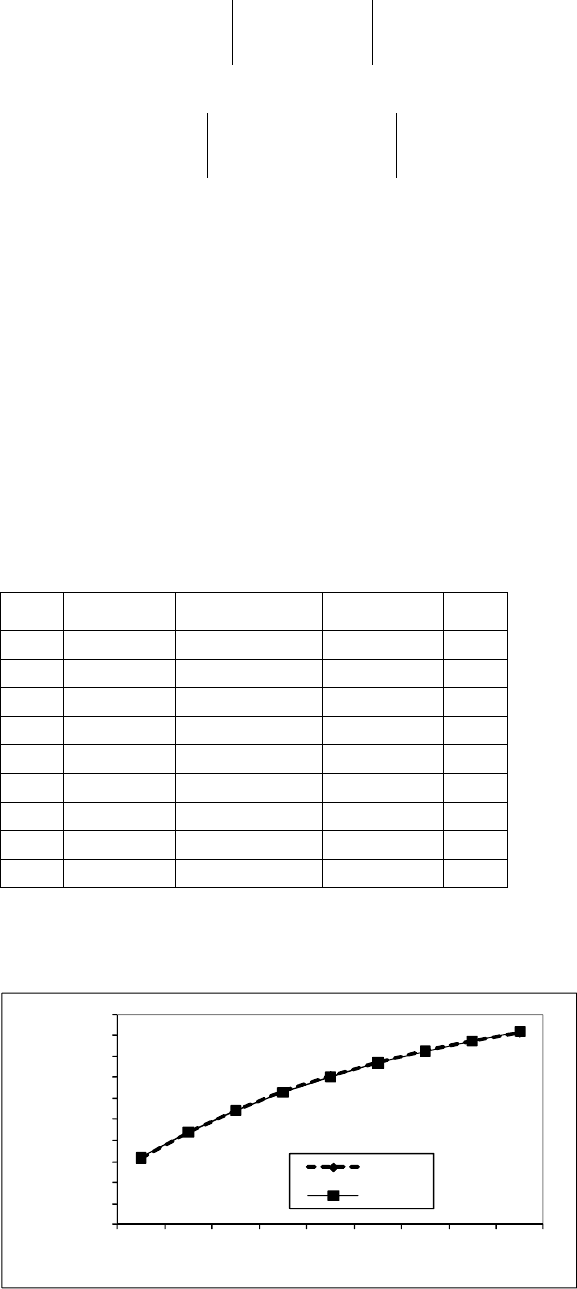
M=
62,186695
8,4616462
Используя X=L
-1
M, получим
Х=
-0,027014151
1,133751527
где a= 1,133751527, b= -0,027014151, отсюда эмпирическая зависимость
у=а+b/х при найденных значениях a и b принимает вид:
y=1,1337515+-0,0270142/x.
Для определения точности выбора эмпирической кривой, т.е. макси-
мального отклонения табличных значений от аппроксимирующей кривой
y=1,1337515+-0,0270142/x составим сравнительную табл. 6.22:
Таблица 6.22
Результаты отклонений табличных значений от значений, вычисленных по
эмпирической формуле y=1,1337515+-0,0270142/x
x
i
y
i
y
i
выч
γ
i
%
0,1 0,863305
0,86361002 0,000305 0,04
0,11
0,887703
0,888168339
0,000465 0,05
0,12
0,908534
0,908633605
9,99*10
-
05
0,01
0,13
0,92634 0,925950368
0,00039 0,04
0,14
0,941549
0,940793308
0,000756 0,08
0,15
0,954499
0,953657189
0,000841 0,09
0,16
0,965457
0,964913085
0,000544 0,06
0,17
0,974639
0,974844759
0,000205 0,02
0,18
0,982218
0,983672912
0,001455 0,15
Результаты отклонений табличных значений от вычисленных по эмпи-
рической формуле представлены на рис. 6.39.
0,8
0,82
0,84
0,86
0,88
0,9
0,92
0,94
0,96
0,98
1
0,1 0,11 0,12 0,13 0,14 0,15 0,16 0,17 0,18
Yi,Yiвыч
Xi
Yi
Yiвыч
Рис. 6.39. Результаты отклонений табличных значений от значений, вычисленных
по эмпирической формуле y=1,1337515+-0,0270142/x
668
Таким образом, размах отклонений значений табличных от вычислен-
ных 9,99*10
-05
0,001455, среднее взвешенное отклонение составляет 0,01 ÷
0,15%, что дает основание подтвердить точность выбранной эмпирической
кривой.
Результаты исследования зависимостей основных характеристик эф-
фективности оптимального СР от интенсивности прибытия ТС к стоп –линии
представлены в табл. 6.23.
Таблица 6.23
Зависимость эффективности оптимального регулирования от
интенсивности прибытия ТС к стоп-линии перекрестка
Характери-
стика
Вид зависимости Уравнение зависимости Погреш-
ность, %
k=tgα
дробно-рациональная y=1/(-3,6130250*x+0,8478542) 0,00 ÷ 0,06
H гиперболическая функ-
ция специального вида
y=1,1201201+-0,0243107/x 0,00 ÷ 0,13
n
0j
/n
maxj
гиперболическая функ-
ция специального вида
y=1,1337515+-0,0270142/x 0,01 ÷ 0,15
Итак, описанные здесь исследования методов, из представленных в тео-
ретических главах монографии (главы 2, 3), где рассматривается управление
дорожным движением, подтверждают их правомерность и работоспособ-
ность в аналитическом аспекте. Эта очевидность иллюстрирована в 23 таб-
лицах и 39 рисунках. Применение аппроксимированного моделирования по-
зволяет глубже изучить механизмы оптимальности в СР. Выявлены пределы
и механизмы оптимальности, но, несмотря на это, НИР следует продолжить.
669
7. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЗАВИСИМОСТИ ШИРИНЫ
ПОЛОСЫ ДВИЖЕНИЯ ОТ ДИНАМИЧЕСКИХ ПРОДОЛЬНЫХ,
ПОПЕРЕЧНЫХ И ВЕРТИКАЛЬНЫХ ГАБАРИТОВ ТРАНСПОРТНЫХ
СРЕДСТВ
В ряде западных стран, в частности в США, вопросы организации до-
рожного движения решены на верхнем пределе инженерных решений (до-
рожные сети с пересечениями в разных уровнях, системы скоростных авто-
магистралей с адаптивным управлением ТП, должными дорожными усло-
виями а также с информацией о коэффициенте сцепления и т.п..), несмотря
на то что ежегодно от ДТП получают смертельные травмы 40-50 тыс. чело-
век [141].
Причинами аварийности, по нашему мнению могут быть, во – первых,
высокая плотность ТП, при движении ТС крайне недостаточные пространст-
венные (временные) интервалы между ними в ТП, во – вторых, размеры ши-
рины полос движения на проезжих частях не соответствуют интенсивным
режимам движения. Первые связаны с максимальной плотностью потоков и
скоростью движения, вторые- с отсутствием пространственной возможности
избежать наезд на автомобиль, снизивший скорость движения.
7.1. Математическая модель зависимостей ширины полосы движения на
проезжей части от продольных, поперечны
и вертикальных габаритов
Дорожное движение состоит из совокупности движений и маневров от-
дельных ТС, образующих ТП, и является по сути результатом взаимодейст-
вия подсистем среда- водитель -автомобиль- дорога -движение- среда
(СВАДДС). Основной его особенностью является охват бесконечного мно-
жества случайно действующих, а порой достаточно часто действительно не-
зависимо их составляющих компонентов.
Условия движения (УД) – это по сути реальная среда ,в которой движет-
ся автомобиль в данный момент времени. Сюда входят дорожные условия,
разновидности ТП, состояние окружающей среды- метеорологические усло-
вия
670
