Живоглядов В.Г. Теория движения транспортных и пешеходных потоков
Подождите немного. Документ загружается.


но здесь К = 0, r = A
1
, и, следовательно
,1
1
2121
m
i
m
аiхLmх
точно так же
m
i
m
аi
1
1
,1
где
аiхаiх 11
1
откуда
m
i
m
аiхLmmх
1
2111
,1
средние значения промежутков будут
./,/ nххnхх
mm
б) Здесь
1`122
, и цикл
`11
может укладываться несколько
раз в цикл
22
. Тем не менее счет ведем по циклам
11
. Если в первом
цикле А
1
+ В
1
начало цикла А
2
+ В
2
сдвинуть на х, то в следующем цикле А
1
+
В
1
начало сдвинуто на (х + А
2
+ В
2
– А
1
– В
1
).
Однако, учитывая периодичность функции
х
с периодом А
2
+ В
2
,
можно отсчет вести от правого конца, т.е. взять х +
1122
n и про-
водить сквозную нумерацию циклов справа налево. Иными словами, можно
взять: - для свободных промежутков времени
m
i
m
i
m
i
m
iхLm
iхinхх
1
112121
1
11
1
1122
.1
1
(3.14)
для блокированных промежутков
.1
1
1
11
212111
1
111
m
i
m
i
m
iхL
mmiхх
(3.15)
Средние свободные и блокированные промежутки определяются также:
nххА
m
/)(
,
nххВ
m
/)(
(3.16)
В общем случае можно записать
321

;1
1
m
i
m
аiхх
,1
1
1
1
аiхх
m
i
m
(3.17)
где
112222112211
:при //
2211
при >
11
Следует только иметь ввиду, что при А
2
+ В
2
>А
1
+ В
1
счет идет справа
налево, начиная с (m - 1) цикла А
2
+ В
2
и заканчивая вторым циклом [70, 72].
Оба пересекающихся потока стационарны с циклами А
1
+ В
1
и А
2
+ В
2
,
но они могут быть смещены один относительно другого. Это смешение мо-
жет быть с плотностью
(х) свободных промежутков и (х) - блокированных
промежутков второго потока относительно первого. Средние значения сво-
бодных и блокированных промежутков мы можем определить соотношения-
ми [248]
,
0
dххх
dххх
0
(3.18)
Для вычисления здесь может быть использована периодичность
А
(х) и
В
(х) с периодом А
2
+ В
2
, но по-видимому, проще сделать преобразование
этих интервалов следующим образом [70, 72]: сделаем приближенные оценки
для подсчета математических ожиданий. Пусть
(х) – плотность свободных
промежутков
dххх
0
имеем
...
22
22
22
22
2
1
1
2
)(00
dхххdхххAdхххAdххх
mm
mВА
А
Вообще
.)1(
11
22
0
2222
0
1
1
2
122
22
dyyiy
dyyiyiAdххх
ii
i
а =
322
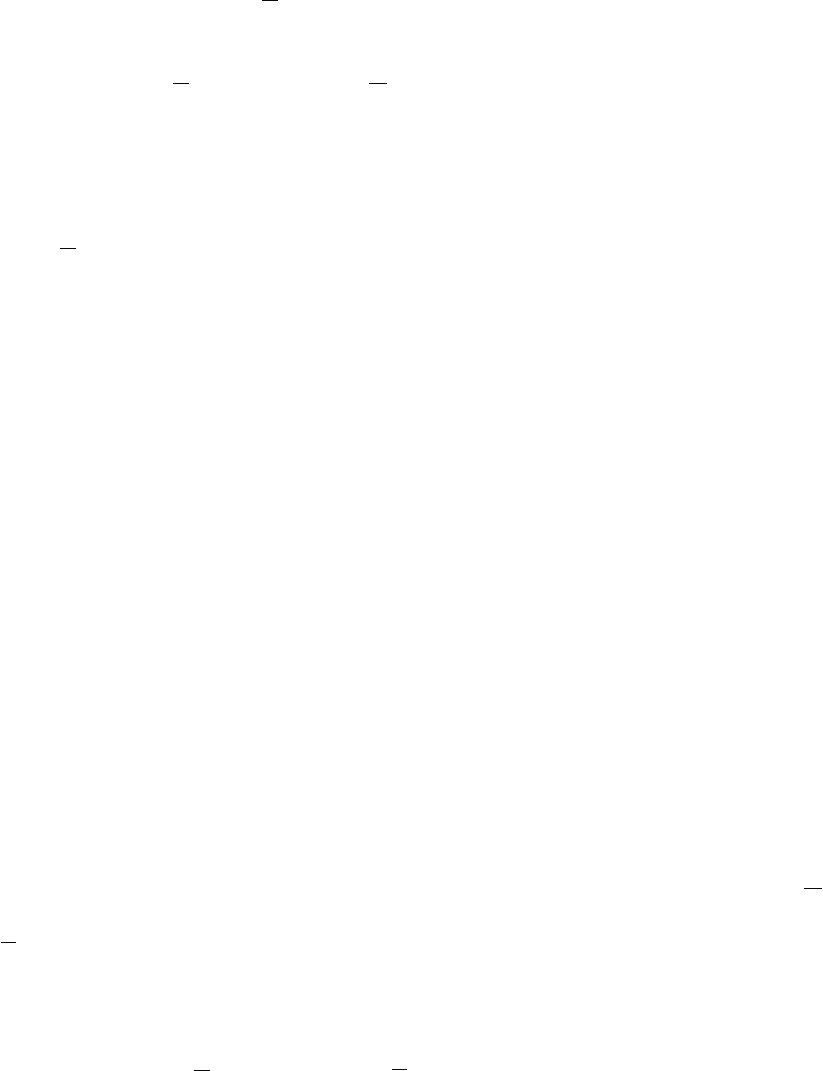
За счет периодичности
A
(х) с периодом А
2
+ В
2
0
22
00
2
i
dyyiydхххА
(3.19)
Вычислим
/ndууΒΑiajуφdууΒΑiуА
m
j
Α
Α
Α
22
1
0
22
0
1
22
/ndyyΒΑiаjjyLΡΒrΕΒrΚΑ
m
ij
Α
i
2
0
22222
1
(3.20)
где
dуyi
i
2
0
22
;
dуyΒΑiΒrEΒriayHdуyΒΑijayL
ΑΑ
22
0
222222
0
dуyΒΑirjayHdyyΒΑirΑjayH
ΑΑ
22
0
22
0
2
22
.
2
0
222
dyyΒΑiΑjayH
Α
(3.21)
Аналогично будет и для
i
, только вместо
будет
, а вместо
(х)
будет
B
(х). При этом еще нужно учитывать сдвиг смещения х на А
2
в приня-
том способе оценки смещения. Поэтому, например формула (3.18) имеет вид
dy.yΒΑiyΑdхχωхBΒ
i
ΒΑ
A
22
1
0
22
2
(3.22)
Отсюда изменяются и последующие расчеты. При этом
(х) и
(х) –
соответственно плотности свободных и блокированных промежутков второго
потока.
Для трех потоков надо сначала найти средние В и А двух первых пото-
ков, а затем, отправляясь от этого, присоединить третий к комбинации пер-
вых двух. Для четырех потоков делается так же, рассматривая последова-
тельно первые два, их комбинации с третьим, а затем комбинацию трех пото-
323
ков с четвертым.
3.4. Пропускная способность нерегулируемого перекрестка при
движении двух потоков в одном направлении
Сделаем теперь оценку пропускной способности перекрестка, считая,
что на первом направлении движутся только два потока, например,
1
1
и
2
1
.
Это справедливо при запрещении левого поворота на перекрестке для этого
направления или при двухрядном проезде перекрестка и оценке движения в
каждом ряду (первый ряд с движением прямо и направо, другой - левый по-
ворот и разворот). В последнем случае рассмотрим первый ряд с прямым
движением и правым поворотом. Для прямого движения (
1
1
) автомобиль
должен пересечь два потока, а для поворота направо (
2
1
) -только один поток,
т.е. с которым он совершит слияние. При проезде перекрестка автомобилем
потока (
1
1
) нужно время пересечения первого потока Т
1
1
(4
1
) и второго Т
1
1
(2
1
),
а для поворота направо - время Т
2
1
(4
1
) [70, 72].
Интенсивности пересекаемых потоков на главной магистрали обозна-
чены
1
4
и
1
2
.
Свободные и блокированные промежутки для автомобилей потока
1
1
определяем по методу, изложенному в предыдущем разделе 3.3, исходя из А
1
1
+ В
1
1
+А
1
2
– В
1
2
, а для потока
2
1
- В разделе 3.2, обозначая А
2
1
+ В
2
1
.
Заметим, что условия пересечения А
1
1
+В
1
1
и А
2
1
+ В
2
1
одного и того же
первого пересекаемого потока автомобилями из
1
1
и из
2
1
, могут быть разны-
ми, так как Т
1
1
(4
1
) и Т
2
1
(4
1
) - время пересечения потока
1
4
у них может быть
разным.
Для каждого потока
1
1
и
2
1
справедливы оценки, аналогично приве-
денным в конце раздела 3.2 [70, 72].
,ΑτΒΑλ
1
2
1
1
1
2
1
2
1
1
ΑτΒΑλ
2
1
2
1
2
1
2
1
(3.23)
Кроме того, один из потоков
1
1
,
2
1
при проезде перекрестка уступает,
время свободного проезда другому потоку. Для оценки этого факта срав-
ним время проезда автомобиля потока
1
1
, через перекресток Т
1
1
(4
1
) – Т
1
1
(2
1
)
324

со временем проезда Т
2
1
(4
1
) автомобиля второго потока
2
1
. Если Т
2
1
(4
1
)
Т
1
1
(4
1
), то автомобили потока
2
1
занимают время проезда автомобилей по-
тока
1
1
.
Точнее, автомобили потока
2
1
будут содержаться в числе ТС потока
1
1
при свободном проезде последних через перекресток, но наоборот может
не быть, т.е. ТС потока
2
1
могут проехать и тогда, когда ТС потока
1
1
про-
ехать перекресток не могут. Следовательно, должно выполняться ограниче-
ние на суммарное движение потоков. В рассматриваемой ситуации будет
2
1
1
2
, и оба потока
1
1
и
2
1
, должны укладываться в возможность проезда
перекрестка при определенном накоплении в очереди, т.е. при некотором
0
1
,
1
2
1
1
1
2
1
2
1
1
2
1
2
1
2
1
2
1
ΑτΒΑλτΒΑλ
и
1
2
2
1
2
1
2
1
2
1
2
1
1 ΑΑτΒΑλ
.
Складывая эти неравенства, найдем
2
1
1
1
1
2
1
2
1
1
2
1
2
1
2
1
2
1
Однако это возможно только при Т
2
1
(4
1
)
Т
1
1
(4
1
), так как здесь А
1
2
А
2
1
.
Если же Т
2
1
(4
1
) > Т
1
1
(4
1
), то эти рассуждения не подходят, потому что здесь
автомобиль потока
1
1
может пройти тогда, когда автомобиль потока
2
1
не
пройдет из-за Т
2
1
(4
1
) > (4
1
).
Может быть также и наоборот: ТЕ потока
2
1
, может пройти, тогда как
ТЕ потока
1
1
не пройдет, так как потоку
1
1
требуется пересечь другой поток
2
1
. Возможен также случай, когда оба потока
1
1
и
2
1
проходят через пере-
кресток. Следовательно, А
1
2
и А
2
1
не содержатся друг в друге, но могут иметь
общую часть. Найдем ее.
Для этого нужно заново определить А
1
2
и В
1
2
, считая, что Т
1
= Т
2
1
(4
1
),
где Т
1
- время пересечения первого потока
1
4
потоком
1
1
.
В этом случае
1
2
А будет содержаться и в
1
2
и в
2
1
, т.е. это будет их
общая часть. В этой общей части будут находиться некоторые части от каж-
325

0
дого потока ,,
2
1
1
1
т.е. при ,10
1
10
2
1
2
1
1
1
2
1
2
1
11
2
1
2
1
2
1
2
12
ΑτΒΑλρτΒΑλρ
Кроме того, должно быть
1
2
1
2
1
1
1
2
1
2
1
11
1 АΑτΒΑλρ ;
.АΑτΒΑλρ
1
2
2
1
2
1
2
1
2
1
2
12
1
Складывая эти неравенства, найдем [70, 72].
.ΑΑΑτΒΑλτΒΑλ
1
2
1
2
2
1
2
1
2
1
2
1
2
1
1
1
1
2
1
2
1
1
2 (3.24)
Таким образом, окончательно в дополнение к (3.23) должно еще вы-
полняться.
,ΑτΒΑλτΒΑλ
0
2
1
2
1
2
1
2
1
1
1
1
2
1
2
1
1
(3.25)
где
А
2
1
, если Т
2
1
(4
1
)
Т
1
1
(4
1
)
А
2
1
+ А
1
2
– 2
1
2
А , если Т
2
1
(4
1
) > Т
1
1
(4
1
). (3.26)
Итак, для оценки пропускной способности перекрестка по двум пото-
кам надо учитывать соотношение (3.23) и (3.25) и (3.26) [70, 72]. Может воз-
никнуть сомнение в достаточности этих соотношений, т.е. может показаться,
что ТС одного потока, например
1
1
, создают лишнюю задержку и поэтому
нужны дополнительные соотношения. В действительности, из-за стационар-
ности потоков это явление кажущееся, по крайней мере, для оценок в сред-
нем.
Пусть средняя длина интервала есть
11
/1
для первого потока и
22
/1
для второго потока. За каждый такой интервал один поток накапли-
вает в среднем число ТС другого потока. Итак
1212
/
(первый задержи-
вает
12
/
ТС второго потока в среднем) и ./
2121
Так как выполнено соотношение (3.25), то за время (А
1
2
+ В
1
2
) автомо-
били первого потока должны освободить перекресток, если только они не за-
держиваются вторым потоком. В этом предположения (если ТС первого по-
тока не задерживаются вторым потоком) оценим возможность проезда ТС
326
второго потока, задерживаемых первым потоком. Но эти автомобили могут
еще задерживаться за счет несогласованности промежутка их накопления
1
с
промежутком
1
, за который они могут освободиться, т.е. они будут накап-
ливаться еще за счет несогласованности
1
с циклом
21
. Однако можно
считать, что за счет повторений циклов (А
1
+ В
2
) эта разгрузка должна про-
изойти. Повторения должны производиться до повторения исходной фикси-
рованной ситуации. Если
,//
11111
nm
где m
1
и n
1
- целые положитель-
ные числа, и
11111
ΒΑmnγ , то
1112111
ΒΑmλnγλ . При этом ТС должны
разгрузить перекресток и затем прийти к такому же состоянию, что и раннее,
т.е. должно быть
112112
mn
, так как поток стационарный, и мы можем его
сдвигать по времени без изменения числа поступивших автомобилей, доби-
ваясь нулевого положения в фиксированный исходный момент. Тем самым
получается
./)( ),/(/
212111111212
АВАВАА
т.е. получили, что соотношение (3.23) обеспечивает выполнение возможно-
сти проезда ТС второго потока, задержанных за средний интервал между ТС
первого потока, двигающихся без задержки.
Если
11111
// nm
, то рассуждения те же. Следовательно, соотно-
шений (3.23) и (3.25) достаточно для оценки пропускной способности пере-
крестка по отношению к двум потокам.
Если рассмотреть два потока, которые расходятся не сразу, а после пе-
ресечения нескольких потоков, но с разными временами переезда (например,
когда проезжают ТС двух потоков: один поворачивает налево, а другой дела-
ет разворот), то нужно оценить их до момента расхождения, т.е. сосчитать
4
4
4
4
, как свободные, так и блокированные промежутки более длинных по
числу пересечений пересекаемых потоков потоком, и А
3
3
, В
3
3
- для более ко-
ротких потоков (нижние индексы 4 и 3 мы понимаем как число пересекаемых
потоков).
Для этих промежутков выписываем условие (3.23). Для левого поворо-
та и разворота это будет
327

4
4
4
1
4
4
4
4
4
1
3
3
3
1
3
3
3
3
3
1
ΑτΒΑλ;ΑτΒΑλ . (3.27)
Замечание: хотя при развороте автомобиль пересекает четыре потока,
расчет А
4
4
и В
4
4
следует вести по трем потокам, так как пересечение первого
пересекаемого потока происходит дважды. Второе же пересечение, по-
видимому, не следует рассматривать отдельно при определении свободных и
блокированных промежутков.
Время первого пересечения следует оценивать суммой всех времен пе-
ресечения [70, 72], т.е.
).4,4,4()3,3,3,3()2,2,2,2()4,4,4(
3214
1
43214
1
43214
1
4314
1
4
1
ТТТТТ (3.28)
Здесь в скобках указываются все пересекаемые потоки, которым прихо-
дится ждать, а
3214
1
4,4,4 - вторичное пересечение четвертого направления
потоков. В этом случае расчет
4
4
и
4
4
будем вести по трем пересекаемым
направлениям, учитывая второе пересечение первого пересекаемого потока с
начала.
Оценка взаимодействия потоков
3
1
и
4
1
зависит еще от того, как пере-
секаются потоки второго и четвертого направлений, да и третьего направле-
ния также. Здесь может быть общая часть, когда ТС обоих потоков
3
1
,
4
1
могут проходить в одинаковых условиях, а случается, что автомобиль одного
потока проходит, а другого - нет. Общая часть оценивается тем, что при пе-
ресечении одноименных потоков время пересечения должно быть макси-
мальным. Введем величины:
,),4,4(max)4(
4
1
313
11
TTТ
где Т
4
1
- определено перед этим,
.)3,3,3,3(),3,3,3(max)3(
,)2,2,2,2(),2,2(max)2(
43214
1
3213
11
43214
1
313
11
TTТ
TTТ
Определяем теперь
3
A и
3
B по этим максимальным временам пересе-
чение последовательно: Т
1
(4), Т
1
(2), Т
1
(3). Это определит нам свободный
промежуток
3
A , в который пройдут ТС обоих потоков. Вводя, как и раньше
10,10
21
, получим разделение потоков на части. Общая часть
328
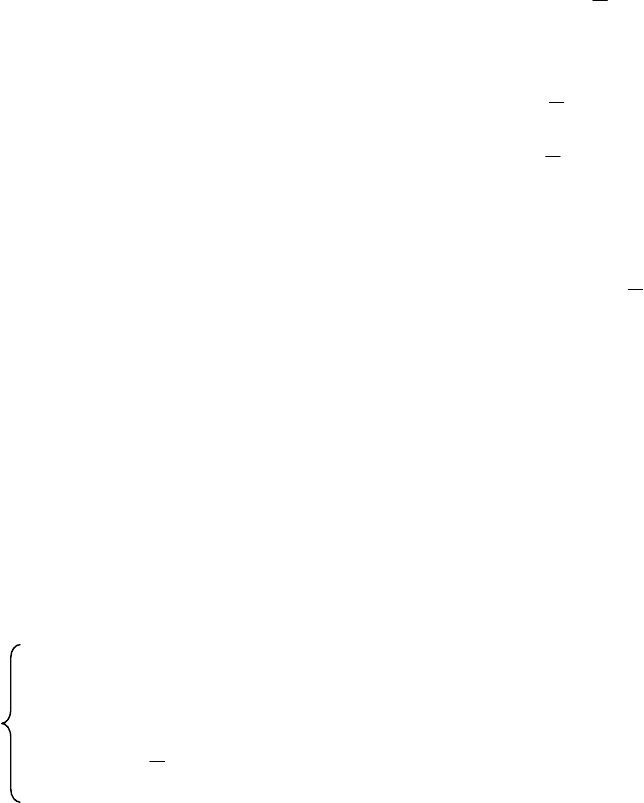
3
3
1
3
3
3
3
3
12
4
1
4
4
4
4
4
11
ΑτΒΑλρτΒΑλρ
и по индивидуальным свободным промежуткам
3
4
4
4
1
4
4
4
4
4
11
1 AΑτΒΑλρ
.AΑτΒΑλρ
3
3
3
3
1
3
3
3
3
3
12
1
Складывая все это, найдем [70, 72]:
.AΑΑτΒΑλτΒΑλ
3
4
4
3
3
3
1
3
3
3
3
3
1
4
1
4
4
4
4
4
1
2
Это происходит, когда один поток из
3
1
и
4
1
не вливается в другой.
Однако возможно, когда один поток вливается в другой. Так будет, когда
время пересечения одного потока не превосходят времени пересечения дру-
гого, т.е. справедливо
,
3
0
3
1
3
3
3
3
3
1
4
1
4
4
4
4
4
1
ΑτΒΑλτΒΑλ (3.29)
где
43214
1
313
1
4
1
313
1
3
1
22222244Τ если ,,,Τ,,ΤΤ,,Α ,
43214
1
3213
1
3,3,3,33,3,3
3
0
А
1
4
, если справедливы одновременно все обратные неравенства (3.30)
А
3
3
+ А
4
4
-
3
А , во всех других случаях.
Рассмотрим теперь общий поток
4
1
3
1
2
1
1
11
и условия проезда
его через перекресток. Для каждого нечетного потока
4
1
3
1
2
1
1
1
,,,
определяем
свободные и блокированные промежутки .,,,,,,,
4
4
4
4
3
3
3
3
1
2
1
2
2
1
2
1
Для ка-
ждого нечетного потока должны выполняться условия (3.23) - (3.26)
4
4
4
1
4
4
4
4
4
1
3
3
3
1
3
3
3
3
3
1
2
1
2
1
2
1
2
1
2
1
1
2
1
1
1
2
1
2
1
1
)(
,)(
,)(
,)(
АВА
АВА
АВА
АВА
(3.31)
Затем должно быть выполнено условие (3.29). Нужны аналогичные
оценки, учитывающие потоки
1
1
и
2
1
. Рассуждениями, подобными выводу
формул (3.24) - (3.29) с учетом (3.25) и (3.30) получается оценка взаимодей-
ствия потока
1
1
с потоком
4
1
3
1
.[70, 72].
329

2
0
4
1
4
4
4
4
4
1
3
1
3
3
3
3
3
1
1
1
1
2
1
2
1
1
)()()( АВАВАВА
(3.32)
где
случае. противном в ,
)2,2,2,2(),2,2,2(min)4( и
),4,4(min)4( если ,
2
3
0
1
2
43214
1
3213
1
11
1
4
1
313
1
11
1
1
2
2
0
AAA
TTТ
TTТА
А
(3.33)
Здесь
2
А определяется как общая часть проезда перекрестка ТС обоих
потоков
3
1
4
1
1
1
и
через потоки второго и четвертого направлений, как это
делалось в разделе 3.3 при времени пересечения, определяемого как
,)2,2,2,2(),2(),2,2,2(max)2(
),4(),4,4(max)4(
43214
1
11
1
3213
12
4
1
11
1
313
12
TTTT
TTTT
А
3
0
определяется из (3.30).
Взаимодействие потока
2
1
с потоками
4
1
3
1
1
1
,,
оценивается аналогич-
ной формулой, выводимой, как и предыдущие:
1
0
4
1
4
4
4
4
4
1
3
1
3
3
3
3
3
1
2
1
2
1
2
1
2
1
1
1
1
2
1
2
1
1
ΑτΒΑλτΒΑλτΒΑλτΒΑλ (3.34)
где
,
2
1
А если Т
1
1
(4
1
)
min{T
3
1
(4
1
, 4
3
), T
2
1
(4
2
), T
4
1
} (3.35)
,
2
0
2
1
А в противном случае.
Здесь А
2
0
взято из (3.33), а
1
А оценивается как общая часть проезда ТС
всех потоков за счет пересечения только потока четвертого направления по
времени пересечения, определяемому как
Т
3
(4) = max{T
3
1
(4
1
, 4
3
), T
1
1
(4
1
), T
2
1
(4
1
), T
4
1
}.
Таким образом, для нормального функционирования перекрестка
должны выполняться все формулы: (3.29), (3.31), (3.32), (3.34). Они выведены
применительно только к первому направлению движения через перекресток,
но аналогичные формулы должны быть выполнены и для остальных направ-
лений [70, 72].
1
0
330
