Живоглядов В.Г. Теория движения транспортных и пешеходных потоков

Подождите немного. Документ загружается.

где a= -0,654143319, b= 0,151463159, отсюда эмпирическая зависимость

у=х/(ах+b) при найденных значениях a и b принимает вид:

y=x/(-0,6541433*x+0,1514632).

Для определения точности выбора эмпирической кривой, т.е. макси-

мального отклонения табличных значений от аппроксимирующей кривой

y=x/(-0,6541433*x+0,1514632) составим сравнительную табл. 2.14

Таблица 2.14

Результаты отклонений табличных значений от значений, вычисленных по

эмпирической формуле y=x/(-0,6541433*x+0,1514632)

выч

0,13 1,957166 1,957108393 0,0000576 0,00

0,14 2,337895 2,337888546 0,0000065 0,00

0,15 2,812005 2,812060914 0,0000559 0,00

0,16 3,418662 3,418786777 0,0001248 0,00

0,17 4,222489 4,222679829 0,0001908 0,00

0,18 5,338281 5,338496025 0,0002150 0,00

0,19 6,991394 6,991481514 0,0000875 0,00

0,2 9,69304 9,692507589 0,0005324 0,01

0,21 14,90448 14,90094926 0,0035307 0,02

Результаты отклонений табличных значений от вычисленных по эмпи-

рической формуле представлены на рис. 2.39.

0,13 0,14 0,15 0,16 0,17 0,18 0,19 0,2 0,21

Yi,Yiвыч

Yiвыч

Рис. 2.39. Результаты отклонений табличных значений от значений, вычисленных

по эмпирической формуле y=x/(-0,6541433*x+0,1514632)

Таким образом, размах отклонений значений табличных от вычислен-

ных 0,0000065  0,0035307, среднее взвешенное отклонение составляет 0,00 

0,02 %, что дает основание подтвердить точность выбранной эмпирической

кривой.

281

5. Изучение зависимости временного интервала, необходимого для

пропуска полной очереди транспортных средств t

от интенсивности при-

бытия к стоп-линии. Для правильного выбора вида аналитической зависимо-

сти выполняются промежуточные вычисления.

0,13 0,14 0,15 0,16 0,17 0,18 0,19 0,2 0,21

Временная длина очереди, с

Интенсивность прибытия, ТЕ/с

Рис. 2.40. Зависимость временного интервала, необходимого для пропуска полной

очереди транспортных средств t

и от интенсивности прибытия

На отрезке изменения переменной x, т.е. х



[0,13; 0,21] выберем точки

= 0,13 и х

= 0,21 наиболее удаленных друг от друга (крайние).

Далее вычисляем х

арм

, х

геом

, х

гарм

по формулам (2.265) и на графике гео-

метрически находятся соответствующие значения переменной у. По данным

табл. 2.3 рассчитываем у

арм

, у

геом

, у

гарм

, при этом используем формулы

(2.266).

арм

0,17

арм

18,5669885

9,464202

геом

0,165227

геом

12,09268782

7,449666

гарм

0,160588

гарм

7,875972923

7,05834

Сравнивая числовые значения у*

, у*

с у

арм

, у

геом

, у

гарм

и оцени-

вая погрешности проведенных вычислений по формулам (2.267)-(2.273) по-

лучены следующие результаты:

После

этого выбирается

ми- нимальная

геом

4,643022

арм

11,50865

гарм

0,81763

арм

9,102787

геом

2,628486

гарм

1,588229

арм

11,11732

282

погрешность ε из ε

, (i=1, 2,…7).

ε= min (ε

, ε

) =0,817633

Так как ε

совпадает с ε

, то в качестве аналитической зависимости хо-

рошим приближением служит зависимость у=х/(ах+b), с неизвестными пара-

метрами а и b. Для уточнения этих параметров используется МНК. Согласно

этого метода значения параметров функциональной зависимости а и b следу-

ет выбрать так, чтобы сумма квадратов погрешностей была наименьшей

(уравнение (2.274)), т.е. F(а, в) =







baxfy

)),;((( будет минимальной, где ε

= у

– f (x

; a, b) – i-я погрешность (i=1, 2,…7).

Необходимым условием существования минимума функции двух пе-

ременных является равенство нулю всех ее частных производных. Значения

параметров а и b найдем из системы уравнений (2.275). Поскольку зависи-

мость получилась нелинейная, то следует применять преобразование коор-

динат к функции у=х/(ах+b). Преобразовав у=х/(ах+b), получим

1/у=(ах+b)/х=a+b/x, , т.е. Z = A

t + B

, где Z =1/у; A

= b; B

= a; t = 1/x.

Система (2.275) примет следующий вид (случай линейной зависимо-

сти):























znBtA

tztBtA

или























naxb

xaxb

111

/1)/1(

Далее, находятся значения а и b, путем решения системы матричным ме-

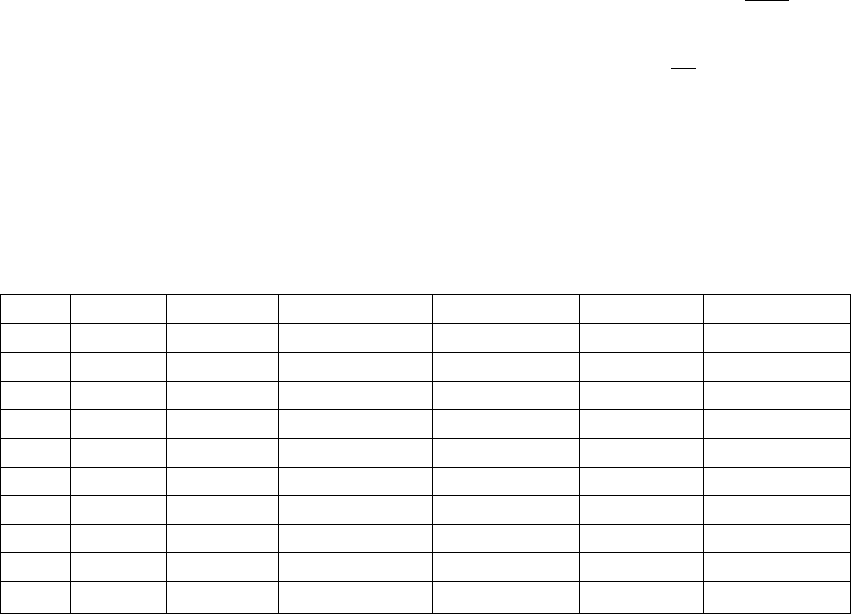
тодом, предварительно осуществив расчеты, которые приведены в табл. 2.15

Таблица 2.15

Данные расчетов для МНК

i x

1/y

1/x

(1/x

)

1/x

1 0,13 4,477987

0,223314628 7,692307692

59,171598

1,717804829

2 0,14 5,321564

0,187914681 7,142857143

51,020408

1,342247719

3 0,15 6,368151

0,157031452 6,666666667

44,444444

1,046876349

4 0,16 7,70246 0,129828652 6,25 39,0625 0,811429076

5 0,17 9,464202

0,105661312 5,882352941

34,602076

0,621537129

6 0,18 11,90145

0,084023375 5,555555556

30,864198

0,466796529

7 0,19 15,50107

0,064511676 5,263157895

27,700831

0,339535135

8 0,2 21,36727

0,046800551 5 25 0,234002753

9 0,21 32,65599

0,030622253 4,761904762

22,675737

0,145820254

∑

1,53 114,7601

1,02970858 54,21480266

334,54179

6,726049774

283

Итак, дана матрица коэффициентов при неизвестных вида:

334,5418

54,2148

а также матрица свободных членов

6,7260498

1,0297086

Используя X=L

-1

M, получим

Х=

0,065739426

-0,28159349

где a= -0,28159349, b=0,065739426, отсюда эмпирическая зависимость

у=х/(ах+b) при найденных значениях a и b принимает вид:

y=x/(-0,2815935*x+0,0657394).

Для определения точности выбора эмпирической кривой, т.е. макси-

мального отклонения табличных значений от аппроксимирующей кривой

y=x/(-0,2815935*x+0,0657394) составим сравнительную табл. 2.16

Таблица 2.16

Результаты отклонений табличных значений от значений, вычисленных по

эмпирической формуле y=x/(-0,2815935*x+0,0657394)

выч

0,13

4,477987

4,462405135

0,0155819

0,35

0,14

5,321564

5,319889301

0,0016747

0,03

0,15

6,368151

6,382869489

0,0147185

0,23

0,16

7,70246

7,735272941

0,0328129

0,43

0,17

9,464202

9,513931888

0,0497299

0,53

0,18

11,90145

11,95806904

0,0566190

0,48

0,19

15,50107

15,52710951

0,0260395

0,17

0,2

21,36727

21,22978251

0,1374875

0,64

0,21

32,65599

31,79509281

0,8608972

2,64

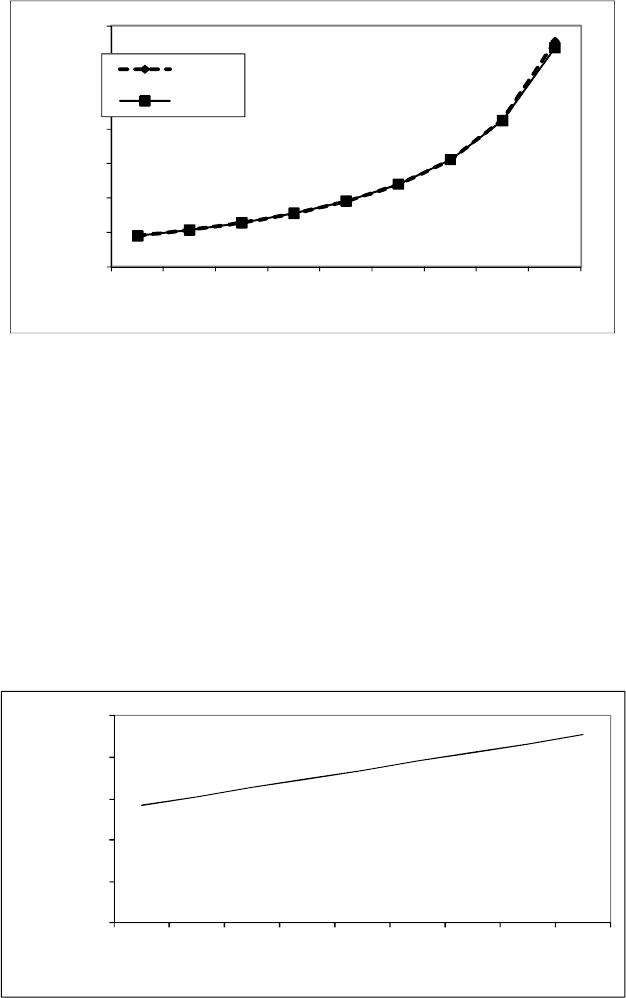
Результаты отклонений табличных значений от вычисленных по эмпи-

рической формуле представлены на рис. 2.41.

Таким образом, размах отклонений значений табличных от вычислен-

ных 0,0016747  0,8608972, среднее взвешенное отклонение составляет 0,03 

2,64 %, что дает основание подтвердить точность выбранной эмпирической

кривой.

284

0,13 0,14 0,15 0,16 0,17 0,18 0,19 0,2 0,21

Yi,Yiвыч

Yiвыч

Рис. 2.41. Результаты отклонений табличных значений от значений, вычисленных

по эмпирической формуле y=x/(-0,2815935*x+0,0657394)

6. Изучение зависимости максимальной пропускной способности перекре-

стка λ

max

от интенсивности прибытия транспортных средств к стоп-

линии. По графику (рис. 2.42) можно предположить, что зависимость носит

линейный характер, однако для правильного выбора вида аналитической за-

висимости выполняются промежуточные вычисления.

0,05

0,1

0,15

0,2

0,25

0,13 0,14 0,15 0,16 0,17 0,18 0,19 0,2 0,21

Максимальная пропускная

способность, ТЕ/с

Интенсивность прибытия, ТЕ/с

Рис. 2.42. Зависимость максимальной пропускной способности перекрестка λ

max

от интен-

сивности прибытия транспортных средств к стоп-линии

На отрезке изменения переменной x, т.е. х



[0,13; 0,21] выберем точки

= 0,13 и х

= 0,21 наиболее удаленных друг от друга (крайние).

Вычисляем х

арм

, х

геом

, х

гарм

по формулам (2.264) и на графике геомет-

рически находятся соответствующие значения переменной у. По данным

табл. 2.3 находятся у

арм

, у

геом

, у

гарм

, при этом используются формулы (2.266):

арм

0,17

арм

0,184625

геом

0,165227

геом

0,179667

0,179554

285

гарм

0,160588

гарм

0,174842

0,174625

Сравнивая числовые значения у*

, у*

с у

арм

, у

геом

, у

гарм

и оцени-

вая погрешности проведенных вычислений по формулам (2.266)-(2.272) по-

лучим следующие результаты:

После этого выбирается минимальная погрешность ε из ε

, (i=1, 2,…7).

ε= min (ε

, ε

) =5,55*10

-17

Так как ε

совпадает с ε

, то в качестве аналитической зависимости хо-

рошим приближением служит зависимость у=ах+b, с неизвестными парамет-

рами а и b. Для уточнения этих параметров используется МНК. Согласно

этого метода значения параметров функциональной зависимости а и b следу-

ет выбрать так, чтобы сумма квадратов погрешностей была наименьшей

(уравнение (2.273)), т.е. F(а, в) =







baxfy

)),;((( будет минимальной, где ε

= у

– f (x

; a, b) – i-я погрешность (i=1, 2,…7).

Необходимым условием существования минимума функции двух пе-

ременных является равенство нулю всех ее частных производных.

Значения параметров а и b найдем из системы уравнений (2.275). Сис-

тема (2.275) примет следующий вид:























ynbxa

yxxbxa

111

)(

Далее находим значения а и b, путем решения системы матричным ме-

тодом расчеты которых приведены в табл. 2.17

арм

5,55

*10

геом

0,004958

гарм

0,009783

арм

0,005071

геом

0,000113

арм

0,01

гарм

0,000217

286

Таблица 2.17

Данные расчетов для МНК

)

0,13

0,142125

0,0169

0,018476

0,14

0,15275

0,0196

0,021385

0,15

0,163375

0,0225

0,024506

0,16

0,174

0,0256

0,02784

0,17

0,184625

0,0289

0,031386

0,18

0,19525

0,0324

0,035145

0,19

0,205875

0,0361

0,039116

0,2

0,2165

0,04

0,0433

0,21

0,227125

0,0441

0,047696

∑

1,53

1,661625

0,2661

0,288851

Итак, дана матрица коэффициентов при неизвестных вида:

0,2661

1,53

а также матрица свободных членов

0,2888513

1,661625

Используя X=L

-1

M, получим

Х=

1,0625

0,004

где a= 1,0625, b= 0,004, отсюда эмпирическая зависимость у=ах+b при най-

денных значениях a и b принимает вид:

у=1,0625*х+ 0,004.

Для определения точности выбора эмпирической кривой, т.е. макси-

мального отклонения табличных значений от аппроксимирующей прямой

у=1,0625*х+ 0,004, составим сравнительную табл. 2.18

Таблица 2.18

Результаты отклонений табличных значений от значений, вычисленных по

эмпирической формуле у=1,0625*х+ 0,004

выч

0,13

0,142125

1,28*10

0,00

0,14

0,15275

1,19*10

0,00

0,15

0,163375

1,14*10

0,00

0,16

0,174

1,05*10

0,00

0,17

0,184625

9,99*10

0,00

0,18

0,19525

9,44*10

0,00

0,19

0,205875

8,6*10

0,00

0,2

0,2165

7,77*10

0,00

0,21

0,227125

7,22E

0,00

287

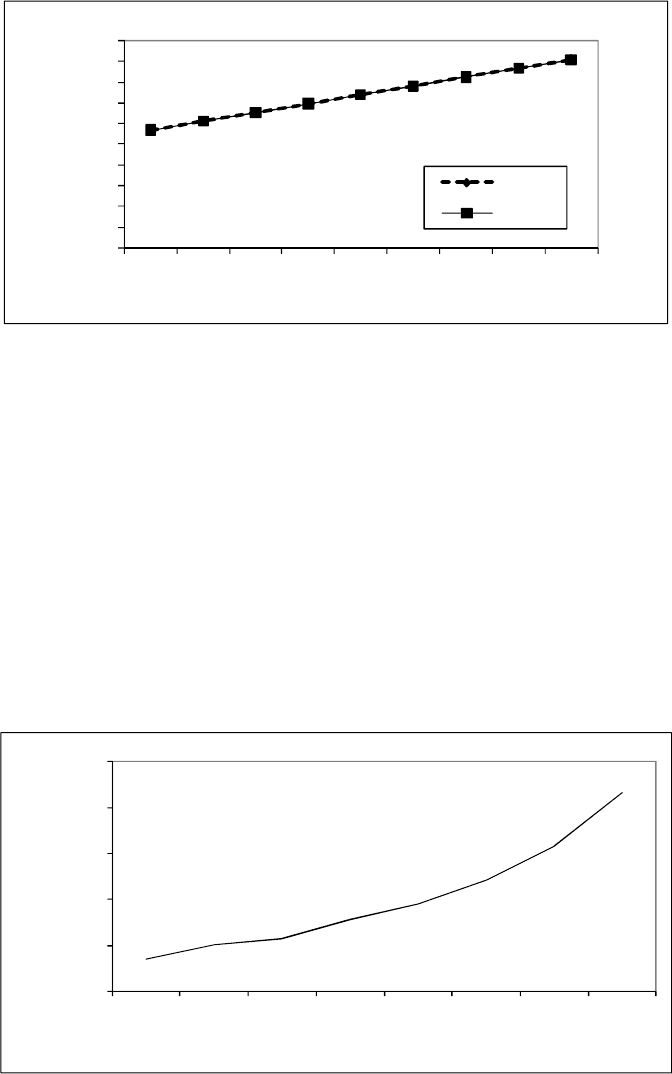
Результаты отклонений табличных значений от вычисленных по эмпи-

рической формуле представлены на рис. 2.43.

0,05

0,1

0,15

0,2

0,25

0,3

0,35

0,4

0,45

0,5

0,13 0,14 0,15 0,16 0,17 0,18 0,19 0,2 0,21

Yi,Yiвыч

Yiвыч

Рис. 2.43. Результаты отклонений табличных значений от значений, вычисленных

по эмпирической формуле у=1,0625*х+ 0,004

Таким образом, размах отклонений значений табличных от вычислен-

ных 7,22E

-16

1,28

-15

, среднее взвешенное отклонение составляет 0,00 %,

что дает основание подтвердить точность выбранной эмпирической прямой.

7. Изучение зависимости задержки одной транспортной единицы от

интенсивности прибытия к стоп-линии (рис. 2.44). Для правильного выбора

вида аналитической зависимости выполняются промежуточные вычисления.

0,13 0,14 0,15 0,16 0,17 0,18 0,19 0,2

Задержка одной транспортной

единицы, с

Интенсивность прибытия, ТЕ/с

Рис. 2.44. Зависимость задержки одной транспортной единицы от интенсивности

прибытия к стоп-линии

На отрезке изменения переменной x, т.е. х



[0,13; 0,21] выберем точки

= 0,13 и х

= 0,21 наиболее удаленных друг от друга (крайние).

Вычисляем х

арм

, х

геом

, х

гарм

по формулам (2.265) и на графике геометри-

чески находятся соответствующие значения переменной у. По данным табл.

288

2.3 находим у

арм

, у

геом

, у

гарм

, при этом используются формулы (2.266).

арм

0,17

арм

18,3414085

9,598404

геом

0,1

65227

геом

10,90459566

8,970462

гарм

0,160588

гарм

6,483155674

8,262413

Сравнивая числовые значения у*

, у*

с у

арм

, у

геом

, у

гарм

и оцени-

вая погрешности проведенных вычислений по формулам (2.267)-(2.273) по-

лучены следующие результаты:

После этого выбирается минимальная погрешность ε из ε

, (i=1, 2,…7).

ε= min (ε

, ε

) =0,817633

Так как ε

совпадает с ε

, то в качестве аналитической зависимости хо-

рошим приближением служит зависимость у= аb

, с неизвестными парамет-

рами а и b. Для уточнения этих параметров используется МНК. Согласно

этого метода значения параметров функциональной зависимости а и b следу-

ет выбрать так, чтобы сумма квадратов погрешностей была наименьшей (см.

уравнение (2.274)), т.е. F(а, в) =







baxfy

)),;((( будет минимальной, где ε

= у

– f (x

; a, b) – i-я погрешность (i=1, 2,…7).

Необходимым условием существования минимума функции двух пе-

ременных является равенство нулю всех ее частных производных. Значения

параметров а и b найдем из системы уравнений (2.275). Поскольку зависи-

мость получилась нелинейная, то следует применять преобразование коор-

динат к функции у=аb

. Прологарифмировав у=аb

, получим lg y=lg a+x*lg b,

т.е. Z = A

t + B

, где Z =lg у; A

= lg b; B

= lg a; t = x.

Система (2.275) примет следующий вид: (случай линейной зависимо-

сти):

арм

8,743005

геом

1,306192

гарм

3,115248

арм

9,370947

геом

1,934134

арм

10,079

гарм

1,779258

289























znBtA

tztBtA

или























ynaxb

yxaxb

111

lglglg

lglg)(lg

Далее, находятся значения а и b, путем решения системы матричным

методом, расчеты которых приведены в табл. 2.19

Таблица 2.19

Данные расчетов для МНК

lgy

1 0,13 3,593627

0,555532998 0,0169 0,0722193

2 0,14 5,119961

0,709266653 0,0196 0,0992973

3 0,15 5,775275

0,761572669 0,0225 0,1142359

4 0,16 7,780795

0,891023973 0,0256 0,1425638

5 0,17 9,598404

0,982199026 0,0289 0,1669738

6 0,18 12,16726

1,085192789 0,0324 0,1953347

7 0,19 15,76356

1,197654304 0,0361 0,2275543

8 0,2 21,62913

1,335039051 0,04 0,2670078

9 0,21 33,08919

1,519686136 0,0441 0,3191341

∑

1,53 114,5172

9,037167598 0,2661 1,6043211

Итак, дана матрица коэффициентов при неизвестных вида:

0,2661

1,53

а также матрица свободных членов

1,6043211

9,0371676

Используя X=L

-1

M, получим

Х=

11,33376972

-0,92261112

где lga=-0,92261112, lgb= 11,33376972, отсюда a=0,119505772, b=2,1566*10

Эмпирическая зависимость у=аb

при найденных значениях a и b принимает

вид

y=0,1195058*215 660 061 038,4450000

Для определения точности выбора эмпирической кривой, т.е. макси-

мального отклонения табличных значений от аппроксимирующей кривой

y=0,1195058*215660061038,4450000

, составим сравнительную табл. 2.20

290