Живоглядов В.Г. Теория движения транспортных и пешеходных потоков

Подождите немного. Документ загружается.

денных значениях a и b принимает вид у= 2,125*х+ 0,008.

Для определения точности выбора эмпирической кривой, т.е. макси-

мального отклонения табличных значений от аппроксимирующей прямой

у= 2,125*х+ 0,008 составим сравнительную табл. 2.8

Таблица 2.8

Результаты отклонений табличных значений от значений, вычисленных по

эмпирической формуле у= 2,125*х+ 0,008

выч

0,13

0,28425

2,55

0,00

0,14

0,3055

2,39*10

0,00

0,15

0,32675

2,28*10

0,00

0,16

0,348

2,11*10

0,00

0,17

0,36925

2*10

0,00

0,18

0,3905

1,89*10

0,00

0,19

0,41175

1,72*10

0,00

0,2

0,433

1,55*10

0,00

0,21

0,45425

1,44*10

0,00

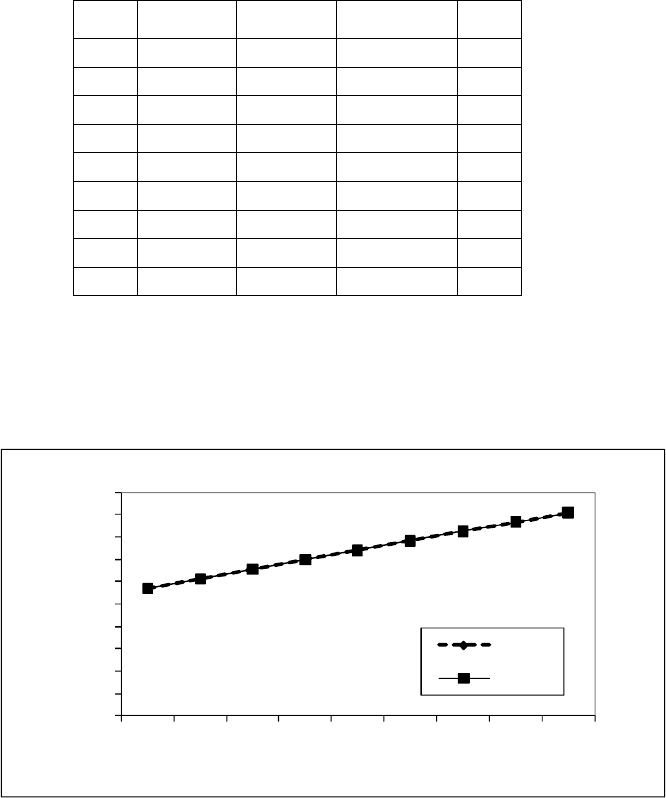
Результаты отклонений табличных значений от вычисленных по эмпи-

рической формуле представлены на рис. 2.34.

0,05

0,1

0,15

0,2

0,25

0,3

0,35

0,4

0,45

0,5

0,13 0,14 0,15 0,16 0,17 0,18 0,19 0,2 0,21

Yi,Yiвыч

Yiвыч

Рис. 2.34. Результаты отклонений табличных значений от значений, вычисленных

по эмпирической формуле у= 2,125*х+ 0,008.

Таким образом, размах отклонений значений табличных от вычислен-

ных 1,44*10

-15

2,55

-15

, среднее взвешенное отклонение - 0,00 %, что дает

основание подтвердить точность выбранной эмпирической прямой.

3. Изучение зависимости длительности цикла С и его основных тактов от

интенсивности. Определим наиболее простую зависимость С(λ). Для пра-

271

вильного выбора вида аналитической зависимости выполняются промежу-

точные вычисления.

На отрезке изменения переменной x, т.е. х



[0,13; 0,21] выберем точки

= 0,13 и х

= 0,21 наиболее удаленных друг от друга (крайние).

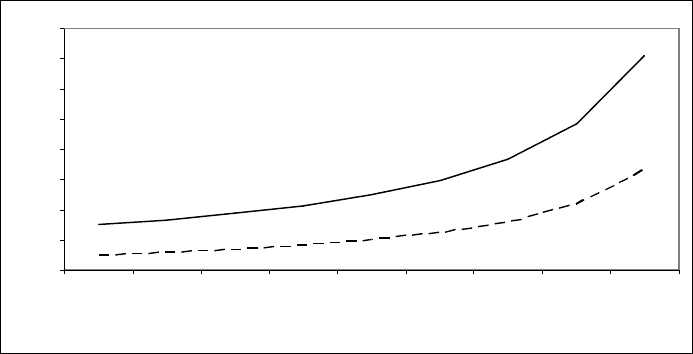
Рис. 2.35. Зависимость длительности цикла С и его разрешающего такта от интен-

сивности прибытия к стоп – линии λ при неизменных геометрических характеристиках

перекрестка

Далее вычисляем х

арм

, х

геом

, х

гарм

по формулам (2.264) и на графике

геометрически находятся соответствующие значения переменной у. По дан-

ным табл. 2.3 рассчитываем у

арм

, у

геом

, у

гарм

, при этом используем формулы

(2.266).

арм

0,17

арм

43,01443

21,63164

геом

0,165227

геом

32,68819

20,84692

гарм

0,160

588

гарм

24,84092

20,08422

Сравнивая числовые значения у*

, у*

с у

арм

, у

геом

, у

гарм

и оцени-

вая погрешности проведенных вычислений по формулам (2.267)-(2.273) по-

лучены следующие результаты:

0,13 0,14 0,15 0,16 0,17 0,18 0,19 0,2 0,21

Интенсивность прибытия, ТЕ/с

зел

272

арм

21,38279

геом

11,05655

гарм

3,209283

арм

22,16751

После этого выбирается минимальная погрешность ε из εi, (i=1, 2,…7).

ε= min (ε

, ε

) =3,209283

Так как ε совпадает с ε 3 , то в качестве аналитической зависимости хо-

рошим приближением служит зависимость у=1/(ах+b), с неизвестными пара-

метрами а и в. Для уточнения этих параметров используется МНК. Согласно

этого метода значения параметров функциональной зависимости а и b следу-

ет выбрать так, чтобы сумма квадратов погрешностей была наименьшей

(уравнение (2.273)), т.е. F (а, в) =







baxfy

)),;((( будет минимальной, где ε

= у

– f (x

; a, b) – i-я погрешность (i=1, 2,…7).

Необходимым условием существования минимума функции двух пе-

ременных является равенство нулю всех ее частных производных.

Значения параметров а и b найдем из системы уравнений (2.274). По-

скольку зависимость получилась нелинейная, то следует применять преобра-

зование координат к функции у=1/(ах+b). Преобразовав у=1/(ах+b), получим:

1/у=ах+в, т.е. Z = A

t + B

, где Z =1/у; A

= a; B

= b; t = x.

Система (2.275) примет следующий вид: (случай линейной зависимо-

сти):























znBtA

tztBtA

или























nbxa

xbxa

111

)(

Далее, находим значения а и b, путем решения системы матричным мето-

дом, предварительно осуществив расчеты, которые приведены в табл. 2.9.

геом

11,84128

арм

22,9302

гарм

4,7567

273

Таблица 2.9

Данные расчетов для МНК

1/y

0,13

15,05512

0,066422586

0,0169

0,0086349

0,14

16,69925

0,059882929

0,0196

0,0083836

0,15

18,7467

0,053342722

0,0225

0,0080014

0,16

21,36663

0,046801952

0,0256

0,0074883

0,17

24,8317

0,040271105

0,0289

0,0068461

0,18

29,65712

0,033718716

0,0324

0,0060694

0,19

36,79681

0,027176269

0,0361

0,0051635

0,2

48,4652

0,020633362

0,04

0,0041267

0,21

70,97373

0,01408972

0,0441

0,0029588

∑

1,53

282,5923

0,36233936

0,2661

0,0576727

Итак, дана матрица коэффициентов при неизвестных вида:

0,2661

1,53

а также матрица свободных членов

0,0576727

0,3623394

Используя X=L

-1

M, получим

Х=

-0,65416051

0,151467216

где a= -0,65416051, b= 0,151467216, отсюда эмпирическая зависимость

у=1/(ах+b) при найденных значениях a и b принимает вид:

у=1/( -0,65416051*х+ 0,151467216).

Для определения точности выбора эмпирической кривой, т.е. макси-

мального отклонения табличных значений от аппроксимирующей кривой

у=1/( -0,65416051*х+ 0,151467216) составим сравнительную табл. 2.10.

Таблица 2.10

Результаты отклонений табличных значений от значений, вычисленных по

эмпирической формуле у=1/( -0,65416051*х+ 0,151467216)

выч

0,13

15,05512

15,05426702

0,000853

0,01

0,14

16,69925

16,69874378

0,000506

0,00

0,15

18,7467

18,74655328

0,000147

0,00

0,16

21,36663

21,366821

0,000191

0,00

0,17

24,8317

24,83859328

0,006893

0,03

0,18

29,65712

29,65746475

0,000345

0,00

0,19

36,79681

36,79620084

0,000609

0,00

0,2

48,4652

48,46108525

0,004115

0,01

0,21

70,97373

70,95465258

0,019077

0,03

274

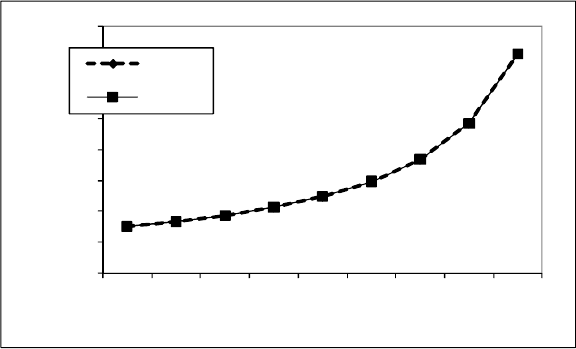
Результаты отклонений табличных значений от вычисленных по эмпи-

рической формуле представлены на рис. 2.36.

0,13 0,14 0,15 0,16 0,17 0,18 0,19 0,2 0,21

Yi,Yiвыч

Yiвыч

Рис. 2.36. Результаты отклонений табличных значений от значений, вычисленных

по эмпирической формуле у=1/( -0,65416051*х+ 0,151467216)

Таким образом, размах отклонений значений табличных от вычислен-

ных 0,000345 0,000191, среднее взвешенное отклонение составляет 0,00 ÷

0,03%, что дает основание подтвердить точность выбранной эмпирической

кривой.

Определим наиболее простую зависимость длительности зеленого сиг-

нала t

зел

от интенсивности движения λ. Для правильного выбора вида анали-

тической зависимости выполняются промежуточные вычисления.

На отрезке изменения переменной x, т.е. х



[0,13; 0,21] выберем точки

= 0,13 и х

= 0,21 наиболее удаленных друг от друга (крайние).

Далее вычисляем х

арм

, х

геом

, х

гарм

по формулам (2.265) и на графике

геометрически находятся соответствующие значения переменной у. По дан-

ным табл. 2.3 рассчитываем у

арм

, у

геом

, у

гарм

, при этом используются форму-

лы (2.266).

арм

0,17

арм

18,75962

9,67149

геом

0,165227

геом

12,50909

7,6758

гарм

0,160588

гарм

8,341178

7,29439

Сравнивая числовые значения у*

, у*

с у

арм

, у

геом

, у

гарм

и оцени-

вая погрешности проведенных вычислений по формулам (2.267)-(2.273) по-

лучим следующие результаты:

275

арм

9,08813

геом

2,837599

гарм

1,330312

арм

11,08382

После этого выбирается минимальная погрешность ε из ε

, (i=1, 2,…7).

ε= min (ε

, ε

) =1,046788

Так как ε

совпадает с ε

, то в качестве аналитической зависимости хо-

рошим приближением служит зависимость у=х/(ах+b), с неизвестными пара-

метрами а и b. Для уточнения этих параметров используется МНК. Согласно

этого метода значения параметров функциональной зависимости а и b следу-

ет выбрать так, чтобы сумма квадратов погрешностей была наименьшей (см.

уравнение (2.273)), т.е. F(а, в) =







baxfy

)),;((( будет минимальной, где ε

– f (x

; a, b) – i-я погрешность (i=1, 2,…7).

Необходимым условием существования минимума функции двух пе-

ременных является равенство нулю всех ее частных производных.

Значения параметров а и b найдем из системы уравнений (2.275):















0),(

baF

или



























.0)),;(((

0)),;(((

fbaxfy

Поскольку зависимость получилась нелинейная, то следует применять

преобразование координат к функции у=х/(ах+b):

Преобразовав у=х/(ах+b), получим 1/у=(ах+b)/х=a+b/x, , т.е. Z = A

t +

, где Z =1/у; A

= b; B

= a; t = 1/x.

Система (2.275) примет следующий вид: (случай линейной зависимо-

сти):























znBtA

tztBtA

или























naxb

xaxb

111

/1)/1(

Далее, находятся значения а и b, путем решения системы матричным ме-

геом

4,83329

арм

11,46523

гарм

1,046788

276

тодом, предварительно осуществив расчеты, которые приведены в табл. 2.11

Таблица 2.11

Данные расчетов для МНК

i x

1/y

1/x

(1/x

)

1/x

1 0,13 4,779419

0,209230452 7,692308

59,171598

1,609465019

2 0,14 5,601621

0,178519753 7,142857

51,020408

1,275141096

3 0,15 6,625485

0,150932347 6,666667

44,444444

1,006215646

4 0,16 7,935589

0,126014591 6,25 39,0625 0,787591192

5 0,17 9,671495

0,103396631 5,882353

34,602076

0,608215477

6 0,18 12,0811 0,08277392 5,555556

30,864198

0,459855109

7 0,19 15,65109

0,063893314 5,263158

27,700831

0,336280597

8 0,2 21,48543

0,046543169 5 25 0,232715845

9 0,21 32,73982

0,030543845 4,761905

22,675737

0,145446883

∑

1,53 116,571 0,991848022 54,2148 334,54179

6,460926864

Итак, дана матрица коэффициентов при неизвестных вида:

334,5418

54,2148

а также матрица свободных членов

6,4609269

0,991848

Используя X=L

-1

M, получим

0,06108359

0,257754087

где a= -0,257754087, b= 0,06108359, отсюда эмпирическая зависимость

у=х/(ах+b) при найденных значениях a и b принимает вид

у=х/( -0,257754087*х+ 0,06108359).

Для определения точности выбора эмпирической кривой, т.е. макси-

мального отклонения табличных значений от аппроксимирующей кривой

у=х/( -0,257754087*х+ 0,06108359) составим сравнительную табл. 2.12

277

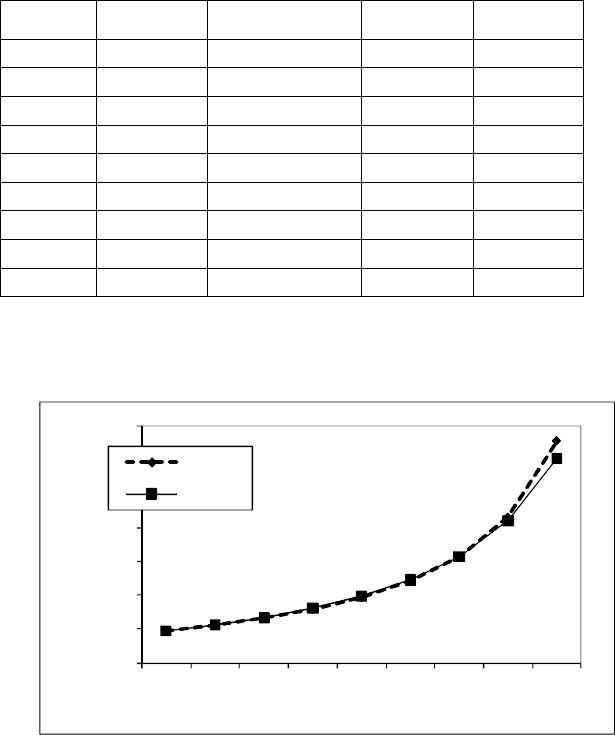
Таблица 2.12

Результаты отклонений табличных значений от значений, вычисленных по

эмпирической формуле у=х/( -0,257754087*х+ 0,06108359)

выч

0,13 4,779419

4,71431963 0,065099

1,36

0,14 5,601621

5,60044393 0,001177

0,02

0,15 6,625485

6,690312474 0,064827

0,98

0,16 7,935589

8,063322647 0,127734

1,61

0,17 9,671495

9,846284599 0,17479 1,81

0,18 12,0811 12,25502306 0,173923

1,44

0,19 15,65109

15,68910601 0,038016

0,24

0,2 21,48543

20,98025386 0,505176

2,35

0,21 32,73982

30,19309671 2,546723

7,78

Результаты отклонений табличных значений от вычисленных по эмпи-

рической формуле представлены на рис. 2.37.

0,13 0,14 0,15 0,16 0,17 0,18 0,19 0,2 0,21

Yi,Yiвыч

Yiвыч

Рис. 2.37. Результаты отклонений табличных значений от значений, вычисленных

по эмпирической формуле у=х/( -0,257754087*х+ 0,06108359)

Таким образом, размах отклонений значений табличных от вычислен-

ных 0,0011772,546723, среднее взвешенное отклонение составляет 0,02 

7,78 %, что дает основание подтвердить точность выбранной эмпирической

кривой.

4. Изучение зависимости полной очереди транспортных средств n

от ин-

тенсивности прибытия. Для правильного выбора вида аналитической зави-

симости выполняются промежуточные вычисления.

На отрезке изменения переменной x, т.е. х



[0,13; 0,21] выберем точки

= 0,13 и х

= 0,21 наиболее удаленных друг от друга (крайние).

278

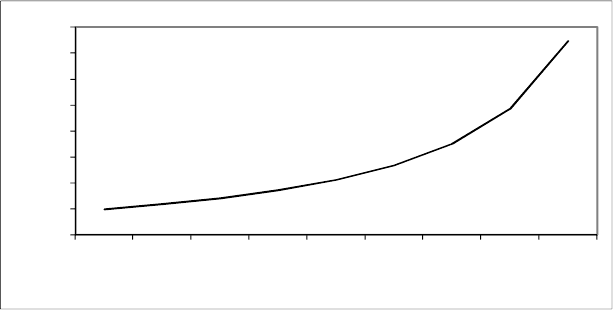
0,13 0,14 0,15 0,16 0,17 0,18 0,19 0,2 0,21

ТЕ

Интенсивность прибытия, ТЕ/с

Рис. 2.38. Зависимость полной очереди транспортных средств n

от интенсивности прибытия

Далее вычисляем х

арм

, х

геом

, х

гарм

по формулам (2.265) и на графике

геометрически находятся соответствующие значения переменной у. По дан-

ным табл. 2.3 рассчитывают у

арм

, у

геом

, у

гарм

, при этом используем формулы

(2.266).

арм

0,17

арм

8,430823

4,222489

геом

0,165227

геом

5,400976

3,298364

гарм

0,160588

гарм

3,459987

3,121749

Сравнивая числовые значения у*

, у*

с у

арм

, у

геом

, у

гарм

и оцени-

вая погрешности проведенных вычислений по формулам (2.267)-(2.273) по-

лучены следующие результаты:

После этого выбирается минимальная погрешность ε из ε

, (i=1, 2,…7).

ε= min (ε

, ε

) =0,338239

Так как ε

совпадает с ε

, то в качестве аналитической зависимости хо-

рошим приближением служит зависимость у=х/(ах+b), с неизвестными пара-

метрами а и b. Для уточнения этих параметров используется МНК. Согласно

этому методу значения параметров функциональной зависимости а и b сле-

дует выбрать так, чтобы сумма квадратов погрешностей была наименьшей

арм

4,208334

геом

1,178487

гарм

0,762502

арм

5,132459

геом

2,102611

арм

5,309074

гарм

0,338239

279

(уравнение (2.273)), т.е. F(а, в) =







baxfy

)),;((( будет минимальной, где ε

= у

– f (x

; a, b) – i-я погрешность (i=1, 2,…7).

Необходимым условием существования минимума функции двух пе-

ременных является равенство нулю всех ее частных производных.

Значения параметров а и b найдем из системы уравнений (2.275).

Поскольку зависимость получилась нелинейная, то следует применять пре-

образование координат к функции у=х/(ах+b): Преобразовав у=х/(ах+b), по-

лучим 1/у=(ах+b)/х=a+b/x, т.е. Z = A

t + B

, где Z =1/у; A

= b; B

= a; t = 1/x.

Система (2.275) примет следующий вид (случай линейной зависимости):























znBtA

tztBtA

или























naxb

xaxb

111

/1)/1(

Далее находим значения а и b, путем решения системы матричным ме-

тодом, предварительно осуществив расчеты, которые приведены в табл. 2.13

Таблица 2.13

Данные расчетов для МНК

i x

1/y

1/x

(1/x

)

1/x

1 0,13 1,957166 0,510942863 7,692308 59,171598 3,930329718

2 0,14 2,337895 0,427735206 7,142857 51,020408 3,055251473

3 0,15 2,812005 0,355618144 6,666667 44,444444 2,370787629

4 0,16 3,418662 0,2925121 6,25 39,0625 1,828200624

5 0,17 4,222489 0,236827142 5,882353 34,602076 1,393100833

6 0,18 5,338281 0,18732622 5,555556 30,864198 1,040701221

7 0,19 6,991394 0,143032992 5,263158 27,700831 0,752805219

8 0,2 9,69304 0,103166808 5 25 0,515834042

9 0,21 14,90448 0,067093921 4,761905 22,675737 0,319494861

∑

1,53 51,67541 2,324255396 54,2148 334,54179 15,20650562

Итак, дана матрица коэффициентов при неизвестных вида:

334,5418

54,2148

а также матрица свободных членов

15,206506

2,3242554

Используя X=L

-1

M, получим

0,151463159

-0,654143319

280