Живоглядов В.Г. Теория движения транспортных и пешеходных потоков

Подождите немного. Документ загружается.

Нормальное функционирование перекрестка обеспечивается для каж-

дой фазы цикла светофора С условием:

 nl ,.....,2,1



(2.127)

Далее,

 должно определяться возможностью пропуска пешеходов по

пешеходной дорожке. Движение пешеходов должно закончиться за время

промежуточного (желтого) такта последней l-ой фазы цикла С светофора, т.е.



 (2.128)

где 



удвоенное, утроенное и т.д., в зависимости от числа фаз, среднее

время пересечения проезжей части пешеходом, движущимся по j-му перехо-

ду. Это время либо является временем пересечения всех проезжих частей

улицы (дороги), либо максимальный временной интервал движения одного

пешехода между островками безопасности и тротуарами или пешеходными

дорожками. В отличие от предыдущего пункта пешеходные переходы нуме-

руются значком j по тому направлению движения автомобилей, которое они

пересекают. Здесь так же различается правый и левый пешеходные потоки с

интенсивностями

ljпj



. Первый из них пересекает j+3 и j+1 направления

по ходу движения и поток пешеходов в этом случае находится - движется

справа, а второй пешеходный поток движется из встречного j+2 направления

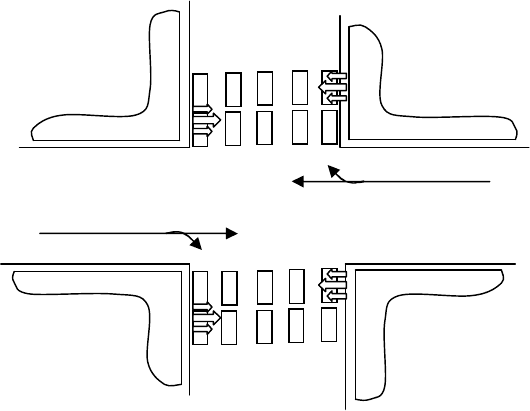
и находится у последнего слева (рис. 2.22).

j +2

j =1

j+2п

jл

j+2л

jп

Рис. 2.22 Нумерация пешеходных потоков на j и j+2 направлени-

ях движения транспортных средств

171

Заметим, что неравенство (2.127) в применении к «широкой» дороге с

несколькими частями в каждом направлении – с многорядным движением

обеспечивает безопасность пешеходов. Для «узкой» дороги - с однорядным

движением в каждом направлении, его не обязательно использовать, тем бо-

лее, что оно там будет выполняться автоматически.

Оценку промежуточных тактов l - фаз цикла светофора С с дополни-

тельными секциями проведем с учетом пропускной способности пешеходных

переходов. Здесь не ставится задача выбора тех тактов или фаз светофора, по

которым нужно разрешать или не разрешать движение пешеходов, а оцени-

вается пропускная способность, выбор l - фаз, промежуточных тактов l - фаз

циклов светофора C в принятых для данного перекрестка способе и схеме ре-

гулирования движения. Предполагается заранее известным, что для l фазы

цикла С разрешено движение пешеходов по переходам принадлежащим

множеству .

w Для пешеходного перехода j

введем множество рядов





иного направления j или этого же направления j=j

, из которых движущийся

при фазе цикла С по крайней мере один автомобиль может пересечь пеше-

ходный переход j

, и множество





jkl

маневров i, для выполнения которых

автомобиль из ряда k направления j пересекает пешеходный переход j

при l

фазе цикла С. Может оказаться, что несколько тактов или циклов C подряд

разрешают движение пешеходов по переходу j

, а до и после этого располо-

жены такты, не разрешающие движение пешеходов по нему. Такой набор

фаз цикла C будет называться серией. Пронумеруем их индексом S. Пусть

относительно перехода j пишется множество Z

серий фаз за цикл С. Заме-

тим, что каждая серия S

z связана с начальной фазой l

и конечной

. Пешеходы, накопившиеся за цикл С, при нормальном функционирова-

нии перекрестка должны в среднем успеть перейти проезжие части улицы

(дороги) за время действия всех серий фаз цикла С. Временное соотношение,

описывающее это, дает:

172

 

 

,)(

)/(

1 )

( )1(

)(11



   

 



    





j s

s l jjl jlj

sll

ll Ij Hk Ii

jjk

jkljjлjnj

CSCkv





(2.129)

где I

– множество направлений j, из которых автомобили хотя бы одного ви-

да маневра пересекают пешеходный переход j,



njk

) имеет тот же смысл,

что и в неравенстве (2.88), но для различных рядов k, направлений j относи-

тельно пешеходного перехода j

. Неравенство (2.129) предназначено для всех

переходов j

=1,2,…,I. Для членов неравенства (2.129) также должно учиты-

ваться прикрытие одних ТЕ другими, которое понимается как одновремен-

ный проезд различных ТС через пешеходный переход. Однако, как правило,

пересечение перехода автомобилями при разрешенном движении пешеходов

происходит достаточно разреженными потоками, поэтому одновременный

проезд различных ТС через пешеходный переход будет происходить досто-

верно редко. Кроме того, ради безопасности движения пешеходов нецелесо-

образно накладывать слишком жесткие ограничения на их движение по пе-

реходам. Исходя из этого, в соотношениях (2.129) прикрытие одних ТС дру-

гими при пересечении ими пешеходного перехода учитывать не будем. Нера-

венства (2.110)-(2.129) образуют допустимую систему, которой должны

удовлетворять искомые величины

,,,

jkl

С 









. Нужно найти такие

значения этих неизвестных, которые реализовали бы экстремум





min



На основании равенств

rllll

tCC 

)(



и (2.105) находим, что







rll

СntC

/)(



откуда

 

   

,/max1/1minmin

СntСnt

rtl









(2.130)

где min и соответственно max в равенствах (2.130) берутся по всем перемен-

ным задачи. Дадим метод решения задачи (2.130) при ограничениях выраже-

173

ний (2.110)-(2.129). Для конкретного перекрестка с конкретной схемой про-

пуска ТПП и порядком чередовании фаз цикла светофора С уже при записи

соотношения (2.110)-(2.129) сразу определятся значения 0

jkl



. За счет это-

го из (2.112) находятся некоторые .1

jkl



Остальные

jkl



остаются неизвест-

ными. Исходя из конструкции перекрестка и схемы движения на нем опреде-

ляются все





kjl





За счет этого многие соотношения из (2.110)-(2.129)

становятся тривиальными. Например, для некоторых j

и k

, для которых l-я

фаза дает запрет движению, будет 0

С



, а остальные значительно упроща-

ются.

В настоящее время неизвестны готовые методы решения (2.130) с ог-

раничениями (2.110)-(2.129). Это задача математического программирования

с нелинейными ограничениями. Однако, используя специфику задачи, ука-

жем кратко путь ее решения, который не является четким алгоритмом, так

как требует в каждом конкретном случае определенной математической изо-

бретательности. Тем не менее схема решения будет построена на частном

случае в следующем п. 2.4.3, где дается конкретная ее иллюстрация.

Пользуясь соотношением (2.112) для



сложения каждого неравенства

(2.110) при одних l с каждым неравенством (2.110), (2.111) при других l, по-

лучаем систему неравенств, в которой за счет (2.112) исключены



и неко-

торые

jkl



Следует отметить, что неравенства (2.110), (2.111) и последующие

суммы их по l=1, 2, ..., n не все линейно не зависимые, поэтому как в указан-

ных неравенствах, так и в последующих, получаемых сложением, нужно

сразу отбрасывать неравенства, вытекающие из остальных. Благодаря этому

число получающихся неравенств будет сравнительно небольшим. Получаю-

щиеся после l=1, 2, …,n неравенства будут содержать только слагаемое

Сnt

/)(

 и часть переменных

jkl



. Для обеспечения









Сnt

/max

 в них

нужно привести к минимуму те части, которые содержат неизвестные

jkl



решив подходящие задачи на условный экстремум, которые оказываются в

174

общем случае задачами линейного программирования. За счет этого опреде-

ляется максимум









Сnt

/max

 и значения некоторых переменных

jkl



. Ис-

пользуя найденные величины в (2.110), (2.111), можно определить некоторые



, выбирая в них переменные

jkl



так, чтобы обеспечить минимум соответ-

ствующих



. Переменные

 и С находятся из соотношений (2.126)-(2.129),

где, если возможно, также нужно исключить



и перейти к



с подходящим

выбором переменных

jkl



. Таким путем можно решить рассматриваемую

здесь задачу.

Указанный путь трудоемок и не всегда прост, но автору неизвестны

другие пути расчета, оценки тактов, фаз, циклов светофорного регулирова-

ния с дополнительными секциями для конкретных перекрестков.

2.4.3 Метод и логика расчета и оценки циклов светофора с допол-

нительными секциями (частный случай)

Ранее в пп. 2.4.1 и 2.4.2 автором представлена теория функционирова-

ния перекрестка с движением рельсового и нерельсового транспорта в усло-

виях светофорного регулирования с дополнительными секциями. Целесооб-

разно эту теорию проиллюстрировать частным случаем на четырехстороннем

перекрестке, на котором осуществляется трамвайное движение посередине и

однорядное нерельсовое из каждого направления со всеми маневрами.

Математическая модель четырехстороннего перекрестка с дви-

жением рельсового и нерельсового транспорта

Здесь k

=1 для всех j=1, 2, 3, 4, а i=1, 2, 3, 4 при k

=1 и i=1, 2, 3 при

+1=2. Пусть дополнительные секции светофора предназначены для левого

поворота одновременно и трамвая, и нерельсового транспорта из первого на-

правления и для правого поворота нерельсового транспорта из первого на-

правления. Определим три фазы цикла светофора:

Первая – поворот налево из первого направления, совмещенный с ос-

новным зеленым тактом (сигналом) этого направления; разрешено движение

направо нерельсового транспорта из первого направления; для остальных

запрещение движения.

175

Вторая – основной разрешающий (зеленый) такт нечетных направле-

ний с разрешением движения направо нерельсового транспорта первого на-

правления; остальным - запрет движения.

Третий – основной разрешающий такт четных направлений с разреше-

нием движения направо нерельсового транспорта из первого направления,

остальным - запрет.

Рассматриваемые здесь такты, фазы цикла светофорного регулирова-

ния несколько не соответствуют реальному движению в принятом варианте

перекрестка. Предполагается движение трамваев направо при зеленом такте

светофора основной секции. Анализируется такая схема регулирования дви-

жения с целью выявления в методе наиболее тонких моментов с математиче-

ской точки зрения. Для соотношений (2.110)-(2.129) данной задачи можно

сразу определить, что неизвестными

jkl



являются только

,,,,,,,,,

122

113

121

112

111



остальные известны. При этом 1

111





для i=3, 4,

121



=1;

kl3



=1 для всех k и i 1





и 1





для всех k и i, ос-

тальные равны нулю. Для простоты дальнейшей записи обозначим через

.,;;;,;;;

1224

1223

1212

1211

1135

1124

1123

1112

1111



 yyyy

Для этих величин, согласно выражениям (2.120), справедливы соотно-

шения

+ х

= 1, х

+ х

= 1, 0



+ y

= 1, y

+ t

= 1, 0



1. (2.131)

Заметим, что в первой фазе цикла светофора нерельсовые транспорт-

ные единицы, идущие налево, могут прикрываться трамваем, движущимся

налево, а трамваи, «идущие» направо, будут прикрыты нерельсовыми ТС

движущимися направо. Последнее прикрытие незначительно (оно противо-

речит нормативу), но принципиально оно возможно. Доли прикрытия в этих

обоих случаях обозначим соответственно через

2111



и . Во второй фазе воз-

можно прикрытие того же типа, но уже для первого и третьего направлений,

а не только для первого направления, как это было в первой фазе. Для перво-

176

го направления доли прикрытия обозначим соответственно через

2212



и , а

для третьего - через

4234



и соответственно.

В третьей фазе прикрытие того же типа, но только для второго и чет-

вертого направлений. Кроме того, автомобили, поворачивающие направо из

первого направления, могут быть прикрыты автомобилями четвертого на-

правления, движущимися налево, на разворот в обратном направлении и на-

право. В первом случае доли обозначим

2313



и , во втором - через

4333



и , а в

третьем - .,

6353



. и



соответственно. Здесь возможны и другие виды при-

крытия, но с целью упрощения учитывать их не будем.

Аналитические модели. Теория взаимодействия и пропуска потоков

на регулируемом перекрестке в аспекте оптимальности. Несложным, но

громоздким путем соотношения (2.110), (2.111) можно записать в виде:

1) для l=1

,])()([

1221222122

121

112

1111

CTCxyExyyxxat





,][

122

1111

CTCxyxat



 (2.132)

2) для l=2

,])()([

1222442244

114

1132

CTCxyExyxxat





,][

124

123

1132

CTCyyxat





,])()([

1222442244

123

114

1133

CTCxyExyyxxat





,][

124

123

1134

CTCyyxat



 (2.133)

3) для l=3

,,,

333

363

CTCaCTCaCTCa



 (2.134)

,])()([

11736353573635355

CTCxExat





В формулах (2.132), (2.133), (2.134) для краткости введены обозначения

известных величин:

,)1()1(

,)1( ,)1(

4,2,1 3,1

32423232

313231313

3132

322

1111

121

 

 





i i

iiii





177

.)1()1(

,)1()1(

)1()1(

,)1(

4133

4,1

4141

4242

2113

4,1

2121

22226

4,2,1 3,1

42434242

41334141

4,2,1 3,1

22232222

211321215

3132

3131

32324

















 





 



i i

iiii

i i

iiii

Заметим, что в неравенствах (2.134) второе и четвертое неравенства

совпадают.

Величины, входящие в неравенства (2.134), все – не отрицательные, от-

сюда, если выполнено третье неравенство в (2.134), будет выполнено и пер-

вое. Значит, достаточно в неравенствах (2.134) рассмотреть только два нера-

венства: второе и третье. За счет того, что а

> a

и a

> a

в неравенствах

(2.133), следует удалить первые два неравенства.

К соотношениям (2.131)-(2.134) добавляются еще соотношения (2.122),

(2.123). Соотношения (2.122) должны быть указаны для величин х

, х

ввиду предполагаемой однорядности нерельсового ряда первого направле-

ния, а также для у

и у

. В соответствии с определением величин

jkl



для не-

известных величин находим неравенства:

,/ ,/ ,/ ,/ ,/

113512241223112451123

CxCyCyCxxCx



 (2.135)

где )./(1 ,/1 ),/(1

11113

12122

11112





Соотношения (2.126)-(2.128) подсчитываются из конкретных условий

задачи.

Нужно ещё вычислить неравенства вида (2.129) для рассматриваемого

здесь типа перекрестка. Эти неравенства зависят от способа регулирования

движения пешеходов по переходам. Точнее, они зависят от наличия специ-

альных, пешеходных двухтактных светофоров только с зеленым и красным

сигналами [49, 50, 232], а также от принятого принципа управления их сиг-

налами. В случае отсутствия пешеходных светофоров принимается принцип

движения пешеходов на разрешающий такт - зеленый сигнал основного све-

тофора. В рассматриваемом случае будем считать, что специальные пеше-

178

ходные светофоры имеются для каждого перехода. Для второго и четвертого

пешеходного перехода зеленый сигнал включается в момент промежуточно-

го (желтого) такта, предшествующий зеленому такту основной секции транс-

портного светофора, по крайней мере, для одного из нечетных направлений.

Для первого пешеходного перехода его зеленый сигнал включается анало-

гично, но относительно четырех направлении движения транспорта. Для

третьего пешеходного перехода его зеленый сигнал включается в момент

включения желтого такта, предшествующий зеленому такту дополнительной

секции левого поворота автомобилей из первого направления. Примем также,

что островков безопасности ни на одном пешеходном переходе рассматри-

ваемого перекрестка нет. В связи с этим можно считать, что Е

есть среднее

время перехода одного пешехода по j-му переходу, и момент выключения зе-

леного сигнала любого пешеходного светофора определить как момент,

предшествующий на величину





max

выключению желтого такта после

основного зеленого такта транспортного светофора. Здесь максимум берется

по тем j-пешеходным переходам, для которых в данное время был зеленый

сигнал и он должен выключиться. Если пешеходные светофоры отрегулиро-

ваны по иному принципу или их нет, то схема расчета в своей основе сохра-

няется, но будет несколько проще.

Исходя из принятого способа регулирования движения пешеходов, по-

лучаем, что для всех пешеходных переходов схема только одна и состоит для

первого перехода из третьей фазы l=3 транспортного светофора; для третьего

перехода - из двух фаз l=1 и l=3; для второго и четвертого - также из двух фаз

l=1 и l=2. Осюда неравенства (2.122) по порядку номеров переходов с учетом

цикличности фаз цикла транспортного светофора имеют вид:





11511

 CCLCb















321

114222

 CCLCb















;33

221

121

11133

 CCLyCLCb







32144

 CCb



где

179





       

 

     

 

       

 

       

.4444

;3333

;222

;1111

121

LLLL

LLL

LLLLy









































(2.136)

К соотношениям (2.131)-(2.136) присоединяются еще требования

(2.130) и неравенства (2.120), (2.123), (2.127), (2.128).

Покажем, как можно решить задачу (2.123) с указанными ограниче-

ниями. Из неравенств (2.132)-(2.134) исключим некоторые неизвестные.

Складывая каждое неравенство (2.132) с каждым неравенством (2.133), а за-

тем с каждым неравенством (2.134), за счет первого соотношения (2.120) ис-

ключаются все γ

и некоторые из x

и у

. Попутно удаляем лишние неравен-

ства, тривиально следующие из остальных, сравнивая между собой коэффи-

циенты d

. В результате получим неравенства:





,1/

11421

 СSSd



,1/

124

1122

 СSyd



 

;1/

;1/;1/

556

122

1144

124

1125

11424

030

122

1141











СSd

СSyxd

СSSyxd

СSSSxxd

СdСSyxd







(2.137)

где введены новые неизвестные:

180