Живоглядов В.Г. Теория движения транспортных и пешеходных потоков
Подождите немного. Документ загружается.


Подставив в неравенства (2.75)-(2.77) значения s, q, r из уравнений
(2.78), получим соответственно предельные α
1
,α
2
,α
3
:
0
3
00
2
00
1
0
332211
;;
TC
sCt
TC
sCt
TC
rCt
TC
rCt
TC
qCt
TC
qCt
rrrrrr
0
3
0
2
0
1
321
,,
TC
sCt
TC
rCt
TC
qCt
rrr
(2.79)
Можно определить долю разрешающего движение (зеленого) такта l-
фазы α
l
и без цикла С, для чего в уравнения (2.79) подставим значение С из
уравнения (2.74) и получим:
)(3/)21(
,)(3/)21(
,)(3/)21(
003
002
001
33
22
11
srqTtsTsrqt
srqTtrTrsqt
srqTtqTqsrt
rr
rr
rr
(2.80)
где
rrrr
tttt
321
.
Если
,1)/()()/()()/(3)(
0010
TCsCtTCrCtTCtsrqC
rrr
а из уравнения (2.74)
,3)(
0
TCtsrqC
r
откуда
,11;11;11
00
3
00
2
00
1
TC
qCt
TC
rCt
TC
sCt
TC
qCt
TC
sCt
TC
rCt
rrrrrr
то это неравенство можно записать в следующем виде:
.1;1;1
00
3
00
2
00
1
TC
qCt
TC
rCt
TC
sCt
TC
qCt
TC
sCt
TC
rCt
rrrrrr
На основании этих соотношений также определяется доля разрешаю-
щего движение (зеленого) такта α
l
для каждой l-фазы цикла:
;
)(3
)21(
1
0
0
000
1
srqTt
qTqsqt
TC
qCt
TC
sCt
TC
rCt
r
rrrr
;
)(3
)21(
1
0
0
000
2
srqTt
rTrsqt
TC
rCt
TC
sCt
TC
qCt
r
rrrr
(2.81)
.
)(3
)21(
1
0
0
000
3
srqTt
sTssqt
TC
sCt
TC
qCt
TC
rCt
r
rrrr
141
Доля запрещающего движение основного запрещающего (красного)
такта l-фазы светофора β
l
определяется по формулам (2.17)-(2.20) β
l
=1-α
l
. По-
сле подстановки в эту формулу значений α
l
из уравнений (2.81), q из уравне-
ний (2.78), цикла С из уравнений (2.74) и проведения соответствующих пре-
образований получим уравнения, которыми определяется β
l
для трехфазных
циклов светофорного регулирования:
;
)(3
)22(
2
11
0
00
00
11
srqTt
sTrTqsrt
TC
sCrCt
TC
qCt
r
rrr
;
)(3
)()22(
2
11
0
0
00
22
srqTt
sqTrsqt
TC
sCqCt
TC
rCt
r
rrr
(2.82)
.
)(3
)()22(
2
11
0
0
00
33
srqTt
qrTsrqt
TC
qCrCt
TC
sCt
r
rrr
Длительность зеленых тактов t
зел.l
двухфазных циклов определяется по
формулам (2.22)-(2.24), трехфазных циклов – так же, но значения долей ос-
новных (зеленых) тактов α
1
,α
2
,α
3
берутся из уравнений (2.81):
;)21()(2)(
00011
qTqsrtsrCtTCqCtTCt
rrrзел
;)21()(2)(
00022
rTrsrtsqCtTCrCtTCt
rrrзел
(2.83)
;)21()(2)(
00033
sTsqrtrqCtTCsCtTCt
rrrзел
Длительность запрещающего движение (красного) такта l-фазы t
кр l
при
двухфазном цикле СР определяется по уравнению (2.25), при трехфазном –
так же, только доли запрещающих движение тактов цикла СР значения
β
1
,β
2
,β
3
принимаются из уравнения (2.82):
),()22()(2))(1()(
0001011
srTqsrtsrCtqCtTCTCTCt
rrrкр
),()22()(2))(1()(
0002022
sqTrsqtsqCtrCtTCTCTCt
rrrкр
(2.84)
).()22()(2))(1()(
0003033
qrTsqrtqrCtsCtTCTCTCt
rrrкр
2.3.4. Метод и логика расчета и оценки промежуточных тактов трехфазных циклов светофор-
ного регулирования
Промежуточные такты l-фаз Т
l
0
цикла светофора (при
nTnTTTTT
n
l
ll
//
1
0
0
00
3
0
2
0
1
) зависят как от длительности проезда автомо-
билем от стоп-линии до внешних границ пешеходных переходов Т
l
0
при ос-
142

вобождении перекрестка, даже если ТС находятся в момент смены основного
(зеленого) такта на подходах к стоп-линии, так и от времени пропуска пеше-
ходных потоков по переходам (см. раздел 2.2). Оценим каждый из этих фак-
торов в отдельности. Первый из них определяем как среднее время занятости
перекрестка ТС с j=1,2,3,4, i=1,2,3,4. Вероятность появления одной нерельсо-
вой или рельсовой ТЕ направления j с маневром i в последнюю единицу вре-
мени горения зеленого сигнала (такта) определяется как
jj
jj
i
j
t
t
i
j
e
e
eh
1
1
и
TjTj
TjTj
i
j
T
j
t
t
i
T
e
e
eh
1
1
(2.85)
соответственно. В стационарном процессе принимается приближенно веро-
ятность прибытия ТЕ направления j маневра i в последнюю секунду действия
t
зел l
. Тогда среднее время занятости перекрестка определится величинами:
4
1
3
1
,
1
,
1
i i
i
T
i
T
T
T
i
j
i
j
j
j
jj
j
j
hT
R
ThT
R
T (2.86)
где
4
1
3
1
.;
i i
i
TT
i
jj
jj
hRhR
Далее по максимумам Т
j
находим время необходи-
мое ТС на проезд зоны перекрестка (от стоп-линии до внешних контуров пе-
шеходных переходов по направлению движения ТС) Т
am
:
4321
,,,,,,,max
4321 TTTTam
TTTTTTTTT (2.87)
Влияние интенсивности движения пешеходов μ
j
на
n
l
l
TT
1
0
0
такое же,
как и при движении нерельсового транспорта (см. подраздел 2.2). Время за-
траченное на переход проезжей части потоком пешеходов должно быть не
менее суммы Т
0
и части разрешающего (зеленого) такта l - фазы α
l
(С-Т
0
), ос-
тавшейся от пропуска ТЕ, которые движутся направо из j-го направления на-
лево из встречного j+2 направления, т.е.
C
TCTskkC
njjnjj
TTnjjTTnjj
lpjлjjплjjn
333
2
3
2
2222
0022
2
)()/)((
(2.88)
где
i
T
i
T
i
nj
i
nj
njnj 2
,,,
2
- соответственно среднее время занятости пешеходного
перехода рельсовой и нерельсовой транспортной единицей j-го и j+2 направ-
143

лений с маневрами i=2,3 при обеспечении безопасности движения. Используя
соотношения (2.9), (2.10) и неравенство (2.88), для двухфазных циклов СР
имеем:
.2
)(
2
)1(
/)1(
0
333
2
3
2
2222
2
2
0
0
22
Tt
kkC
qCt
tT
rqT
sqr
rTTnjjTTnjj
лjjn
лjnj
r
r
pj
njjnjj
(2.89)
Таким же образом, используя соотношения (2.74) и (2.86) и неравенст-
во (2.88), для трехфазных циклов получим:
.3
)(
3
)1(
/)1(
0
333
2
3
2
2222
2
2
0
0
22
Tt
kkC
qCt
tT
srqT
ssqr
rTTnjjTTnjj
лjjn
лjnj
r
r
pj
njjnjj
(2.90)
и т.д. В неравенстве (2.90) s
pj
имеет множитель 3, а в неравенстве (2.89) s
pj
=2,
3t
r
=1,17с. Если t
r
стремится к нулю, тогда неравенство (2.90) будет значи-
тельно проще. Отметим, что неравенства (2.89) и (2.90) должны выполняться
при всех j=1,2,3,4 с учетом указанной выше цикличности. Для удобства обо-
значим левые части этих неравенств (2.89) и (2.90) через N
j
. Используя нера-
венства (2.87), (2.89), (2.90), находим,
T
0
=max{nT
am
, N
1
,N
2
,N
3
,N
4
}, (2.91)
где n – число фаз в цикле светофора: T
am1
=T
am2
=T
am3
. Величина N
j
число фаз
учитывает в формулах (2.89) и (2.90), а величина S
pj
принимается, только во
времени.
Иногда на перекрестке сложившиеся объективные условия, вытекаю-
щие из геометрических его параметров, требуют применения разной дли-
тельности промежуточных тактов после t
кр l
и t
зел l
. В этом случае метод рас-
чета тот же, только максимумы в Т
0
из уравнения (2.91) берутся раздельно по
нечетным и четным направлениям, а T
am
(см. уравнение (2.91)) используется
соответственно по j=1,3 и j=2,4, т.е.
.
321 amamam
TTT
2.3.5 Метод и логика повышения эффективности использования
пропускной способности регулируемого перекрестка за счет прикрытия
одних транспортных средств другими при его проезде
Основная схема, подлежащая математическому описанию функциони-
рования перекрестка предусматривает, что для каждого конкретного случая в
144
эту схему должны вноситься определенные изменения, отражающие особые
условия данного перекрестка. Например, может оказаться, что на перекрест-
ке трамваи и другие ТС с первого направления при левом повороте (j=1, i=3)
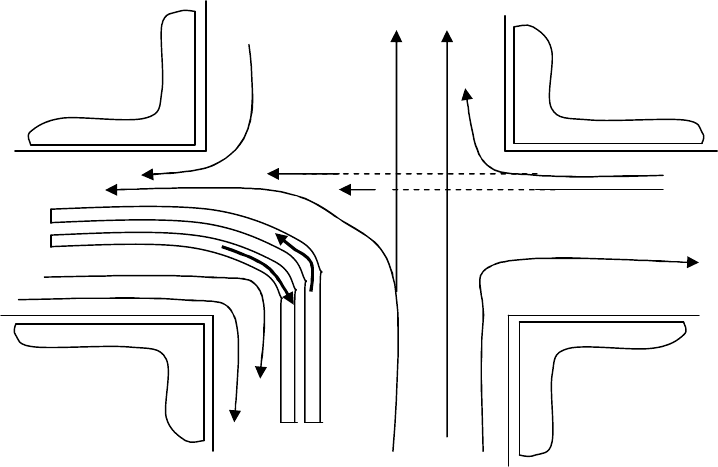
могут двигаться одновременно (рис. 2.14).
На рис. 2.14 изображены нерельсовые транспортные потоки с первого
3
1
1
3
1 i
i
k
k
, второго
2
21
, третьего
2
31
и четвертого
2
41
+
2
42
направлений
движения.
Средняя доля транспортных единиц ,10,
3
1
3
1
которые могут дви-
гаться под прикрытием трамвайных поездов в единицу времени, должна под-
считываться статистически по результатам натуральных наблюдений в каж-
дом случае для конкретных условий движения на данном перекрестке. За
счет этого в формулы (2.1), (2.2) вносят изменения, состоящие в уменьшении
3
1
3
1
на долю прикрытия ,
i
j
т.е.
3
1
3
1
3
1
)1(
, а часть
3
1
3
1
3
1
- прикрытая доля –
поглощается прикрывающей величиной и в формулах (2.1), (2.2) фигуриро-
вать не должна.
Определить
3
1
статистически можно следующим образом. Допустим,
что под прикрытием трамвая пропускаются автомобили с первого направле-
Рис. 2.14 Схема пропуска транспортных средств под прикрытием трамвая с первого
направления j=1, совершающего поворот налево i=3
2
41
j= 1
j+ 1
j+ 2
j+ 3
2
31
3
13
1
21
1
22
2
12
1
12
1
13
1
1
2
42
3
Т14
2
Т43
145
ния с маневром налево i=3. Прежде всего определяется среднее количество
автомобилей, прикрываемых одним трамвайным поездом
3
1p
n на рассматри-
ваемом перекрестке. Тогда
3
1
3
1
3
1
3
1
3
1
3
1
3
1
3
1
3
1
3
1
,1
,/)(
pT
pT
pT
n
n
если
n
(2.92)
где
3
1p
n - (безразмерная) понимается как статистическая оценка математиче-
ского ожидания случайной величины, которая выражает, какую долю при-
крывающего транспорта составляет прикрываемый автомобиль, а также ко-
личество этих долей в прикрывающем, принятом за единицу. Доля прикры-
ваемого в прикрывающем транспорте
i
p
n
1
может быть и дробным числом.
Средние доли транспортных единиц
i
j
, которые могут двигаться в единицу
времени под прикрытием трамвайного поезда или другого автомобиля, до-
пустим, со второго направления j=2, с маневром направо i=2 определяется:
,/)(
3
1
2
1
3
2
2
1
pT
n (2.93)
где
2
1p
n определяется расчетным путем, т.е.
2
1
3
2
2
1
/
Tp
n ;
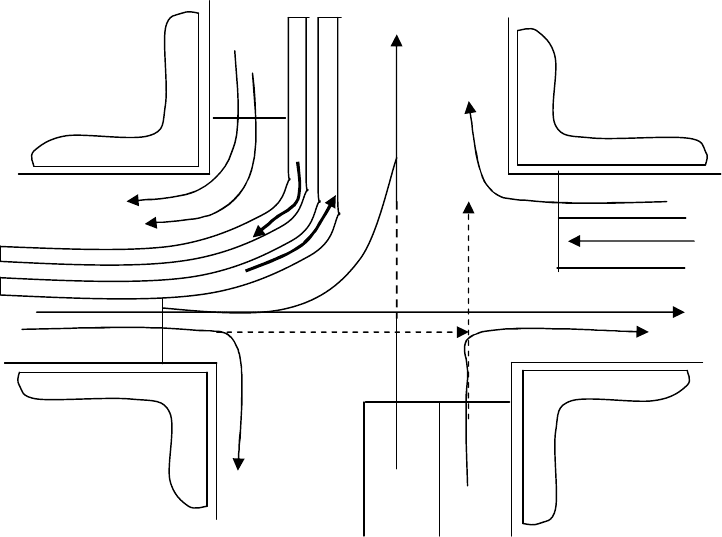
Схема прикрытия трамваем ТС при данном варианте распределения
потоков показана на рис. 2.15.
Рис. 2.16 Схема прикрытия трамваем, осуществляющим левый поворот со второго
направления нерельсовых транспортных средств с j=1, 2, 3, 4; i=1, 2, 3
2
41
j=4
j= 1
j+1= 2
j= 3
2
31
3
22
1
21
1
22
1
31
1
32
2
21
2
12
2
11
146

В соответствии со схемой прикрытия (рис. 2.16) средняя доля прикры-
ваемого в прикрывающем ТП по всем направлениям составит
i
j
n :
./
2
31
2
31
2
41
2
41
2,1
2
1
2
1
3,1
3
1
22
2
31
2
41
2
1
2
1
2
1
3
1
2
3
23
k
kk
k i
i
k
i
k
k
k
k i
i
kT
n
В такой ситуации распределения потоков на перекрестке доля ТС под
прикрытием трамвая составит
./)(
2
31
2
41
2
1
2
1
2
1
3
1
2
3
23
k
k
k i
i
kT
n
под прикрытием автомобиля (первый случай)
,//
2
3
2
3
2
2
1
2
3
2
2
2
1
2
3
2
2
3
p
n (2.94)
где
2
2
1
2
3
2
2
2
1
2
3
2
/
- интенсивность прибытия по первой проезжей
части второго направления j=2, с маневром i=3, которая является частью
3
2
.
В данной формуле доля прикрытия
2
3p
n определяется статистически. Здесь по
первой проезжей части автомобиль, выполняющий маневр направо i=2, дви-
жется в потоке Т с маневрами i=1. На перекрестке в зоне пешеходных пере-
ходов этот автомобиль перестраивается и практически проходит по второй
проезжей части;
под прикрытием трамвая (второй случай)
,2/)(/
2
3
2
3
1
3
1
3
2,1
2
3
2
2,1
3
p
n (2.95)
где
2,1
2p
n определяется расчетным путем,
2
2
1
2
2,1
2 ppp
nnn
;/
2
3
3
2
2,1
2
p
n (2.96)
2
31
2
31
1
31
1
31
2/)(
- интенсивность прибытия по первой проезжей части
третьего направления j=3.
Величина
i
j
зависит не только от соотношения интенсивностей вре-
менных интервалов, но и от геометрических параметров и размеров перекре-
стка, поэтому в основном она определяется статистически. Следует подчерк-
нуть, что прикрытие понимается только как одновременное движение по пе-
рекрестку обоих ТС. Случай, когда в однорядном движении трамвай с i=3,
147
j=3 может двигаться беспрепятственно из-за того, что автомобиль j=1, i=3
сдерживает стоящий за ним поток, к прикрытию не относится. Здесь налицо
нормативная очередность проезда ТП, а это формулами (2.1), (2.2) допуска-
ется как случайность в индивидуальном смысле [45, 248] пуассоновских по-
токов.
Изменения в формулах (2.1), (2.2), (2.91) будут иметь место, если одни
ТС прикрываются другими. Аналогичному изменению подвергнутся и фор-
мулы (2.87)-(2.90). Изменяется при этом величина .
3
2
3
2
3
2
3
2
2222
TnjTjnjjTnjTjnjj
В зависимости от конструктивных особенностей перекрестка один
прикрывающий поток может прикрыть сразу несколько потоков (рисунок
2.15), тогда доли прикрытия
i
j
придется оценивать отдельно статистическим
путем по приведенной выше структуре.
Пропуск автомобилей с маневрами налево и разворота для движения в
обратном направлении i=3,4. Рассмотрим в качестве примера ряд нерельсо-
вого транспорта первого направления j=1. Как известно, при однорядном
движении ТС с маневрами i=3,4 сдерживают стоящие сзади в том же ряду с
другими маневрами. С точки зрения средних оценок и случайности в инди-
видуальном смысле [45, 248] этот факт не требует дополнительных соотно-
шений, так как очередь или микрозатор, созданный в каком-то цикле свето-
фора, ликвидируется за последующие циклы его работы. В среднем при ста-
ционарном потоке на перекрестке и при выполнении условий неравенств
(2.3), (2.6), (2.8) перекресток будет функционировать нормально. Однако мо-
жет потребоваться, чтобы время ликвидации такого микрозатора на конкрет-
ном перекрестке было сокращено. Это достигается методом, аналогичным
описанию в разделе 2.2.
Предложенная система математического описания функционирования
перекрестка применима к любым типам пересечений, с соответствующими
изменениями – коррективами в формулах, выражениях, учитывающих в них
148
схемы ОДД, конфликтование потоков, наличие многих проезжих частей в
каждом направлении и т.п.
Прикрытие в условиях двухрядного, нерельсового движения. Во много-
рядном движении оценки делаются аналогично (рис. 2.14; 2.15). Использу-
ются те же формулы, но величин а
j
определяемых формулами (2.61)-(2.64)
будет несколько больше, так как их надо строить для каждого ряда каждого
направления в отдельности. В случае необходимости здесь также следует
учитывать изложенные выше изменения формулы за счет прикрытия или до-
бавлений типа неравенств (2.4), (2.5). Для нечетных направлений
,;;;max;,max
65432211
aaaaqaaq (2.97)
где
3
1 4,3,1 4,3,1
1
31
1
313232
1
11
1
111212
3
3
3
3
2
3
2
3111
;
i i i
iiii
TTTT
i
T
i
T
a
3
1 4,3,1 4,3,1
1
11
1
111212
1
31
1
313232
3
1
3
1
2
1
2
1332
;
i i i
iiii
TTTT
i
T
i
T
a
2,1 4,3 4,2 3,2
3311323211113
;
i i i i
i
T
i
T
i
T
i
T
iiii
a
4,3,1 4,3,1
3
1
33
3
1
11
1
31
1
31323212124
;
i i i
i
T
i
T
i
i
T
i
T
iiii
a
2,1 4,3 3,2 3,2
3311121231315
;
i i i i
i
T
i
T
i
T
i
T
iiii
a
4,3,1 4,3,1
3
1
33
3
1
11
1
11
1
11121232326
.
i i i
i
T
i
T
i
i
T
i
T
iiii
a
Здесь величины а
1
-а
6
характеризуют среднюю относительную динами-
ческую характеристику ТП – гармоничную длину очереди и величину ее по
каждой проезжей части первого и третьего направлений с учетом того, что
автомобили из других рядов, при некоторых маневрах, как бы вливаются в
рассматриваемые ряды. Так, в
4,3,1 4,3,1
1
31
1
31323211
1
111212
33
3
1
22
1
.
333311
i i
iiii
TT
i
TT
i
T
i
T
a
описывается трамвайный ряд j=1, где очередь составляют трамваи j=1,
i=1,2,3. В этот же ряд войдут трамвайные поезда встречного потока j=3, i=2,3
149
и автомобильные потоки j=1,3, движущиеся по вторым проезжим частям их
направлениям с i=1,3,4, а также по правым, т.е. первым проезжим частям,
только с маневром i=1. Автомобили i=2, К=1 не пересекают потоки и поэто-
му в а
1
не учитываются. Построение а
2
аналогично а
1
.
Отметим, что группы членов правых частей соотношений
4,3,1 4,3,1
1
31
1
31323211
1
111212
i i
iiii
и
4,3,1 4,3,1
1
11
1
111212
1
31
1
313232
i i
iiii
для а
1
и а
2
общие. Следовательно, максимум очереди в трамвайных рядах а
1
и
а
2
в основном зависит от размеров трамвайных потоков
3
1
3
3
3
3
2
3
2
311
i
TTTT
i
T
i
T
и
4,3,1
3
1
3
1
2
1
2
133
i
TTTT
i
T
i
T
.
Величины
2,1 4,3 4,2 3,2
3311323211113
i i i i
i
T
i
T
i
T
i
T
iiii
a
и
2,1 4,3 3,2 3,2
3311121231315
i i i i
i
T
i
T
i
T
i
T
iiii
a
определяют динамические характеристики автомобильных рядов k=1, j=1, 3
соответственно. Метод построения а
3
,а
5
,а
4
,а
6
аналогичен а
1
,а
2
.
Величина q определяет наиболее относительную длинную очередь из
составляющих правую часть равенства а
1
,а
2
,а
3
,а
4
,а
5
,а
6
по нечетным направ-
лениям с точки зрения времени, необходимого ей для выезда на перекресток.
Для четных направлений:
,,,,max;,max
12111092871
aaaaraar (2.98)
где
3
1 4,3,1 4,3,1
1
41
1
414242
1
21
1
212222
3
4
3
4
2
4
2
4227
;
i i i
iiii
TTTT
i
T
i
T
a
3
1 4,3,1 4,3,1
1
21
1
212222
1
41
1
414242
3
2
3
2
2
2
2
2448
;
i i i
iiii
TTTT
i
T
i
T
a
2,1 4,3 3,2 3,2
4422424221219
;
i i i i
i
T
i
T
i
T
i
T
iiii
a
4,3,1 4,3,1
3
1
44
3
1
22
1
41
1
414242222210
;
i i i
i
T
i
T
i
i
T
i
T
iiii
a
150
