Живоглядов В.Г. Теория движения транспортных и пешеходных потоков
Подождите немного. Документ загружается.

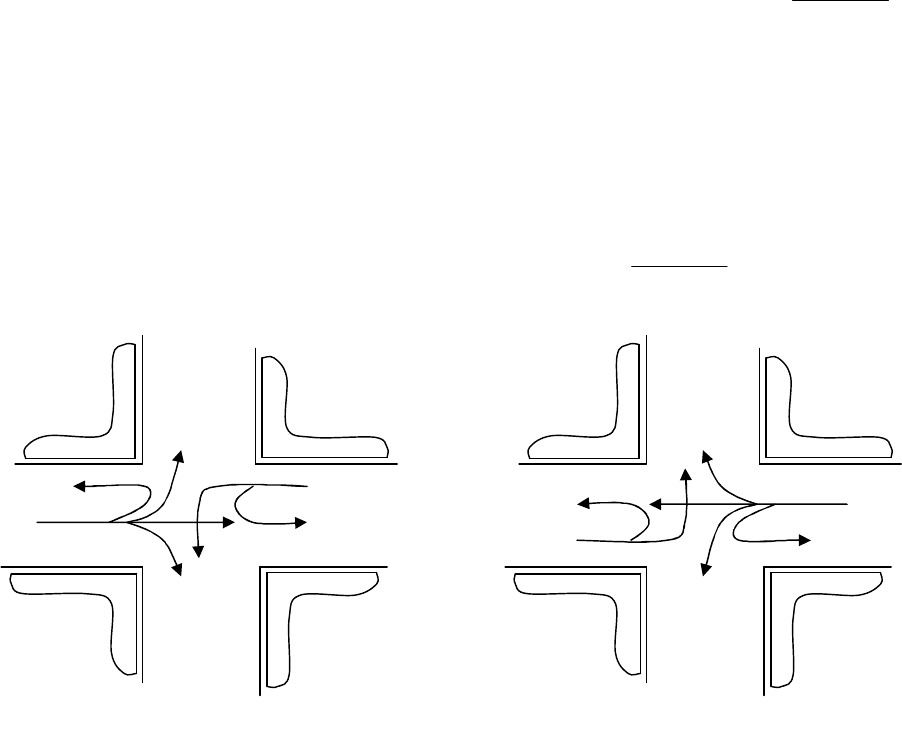
дены пропускать встречные, тем самым, сдерживая следующий за ним и по-
ток. В этом положении автомобиль вливается в поток встречных ТС и дол-
жен какое-то время учитываться в нем как слагаемая величина.
Так, к ТС первого направления j=1 со всеми маневрами
4
1
11
i
ii
прибав-
ляется поток встречного направления поворачивающие налево и разворачи-
вающиеся для движения в обратном направлении
4
3
4
3
3
3
3
3
. Также увели-
чивает время первого направления пропуск пешеходных потоков
лп
лп
kk
31
31
(рис. 2.7, а). Такой же принцип построения динамической характеристики ТП
третьего направления j=3:
4
1
33
i
ii
; к данному потоку прибавляется ТП
встречного первого направления j=1 с маневрами налево и разворота для
движения в обратном направлении
4
1
4
1
3
1
3
1
и ПП
лп
лп
kk
13
13
(рис. 2.7, б).
В таких ситуациях необходимо иметь ввиду это обстоятельство и рас-
сматривать величины, характеризующие пересечения ТПП, как для нечет-
ных, так и для четных направлений движения. Так, динамическая характери-
стика ТПП для нечетных направлений q будет иметь вид:
Рис. 2.7 Схема формирования динамических характеристик ТП первого (а)
и третьего (б) направлений
j + 3 = 4
j +2 =3
j +1 = 2
j =1
j + 3 = 4
j +2 =3
j +1 = 2
j =1
3
3
3
3
2
1
2
1
4
1
4
1
4
3
4
3
1
1
1
1
3
1
3
1
4
1
4
1
3
1
3
1
1
3
1
3
4
3
4
3
3
3
3
3
2
3
2
3
2.7.1 2.7.2
а) б)
111
,
/)(
;/)(
max
4
1
11
4
1
4
1
3
1
3
133
4
1
11
4
3
4
3
3
3
3
311
i
лзплзп
ii
i
злпзлn
ii
q
(2.1)
где
4
1
11
4
3
4
3
3
3
3
311
/)(
i
злтзлn
ii
,
4
1
11
4
1
4
1
3
1
3
133
/)(
i
лзплзп
ii
- динамические характеристики ТПП первого и третьего направлений соот-
ветственно;
лплпзлпзлп 131311
/)(,/)(
- динамические характеристики лишь пешеходных потоков для первого и
третьего направлений соответственно.
Динамическая характеристика ТПП для четных направлений r будет
иметь вид:
,
/)(
;/)(
max
4
1
2424
4
2
4
2
3
2
3
244
4
1
4242
4
4
4
4
3
4
3
422
i
лплп
ii
i
лплn
ii
r
(2.2)
где
4
1
2424
4
2
4
2
3
2
3
244
4
1
4242
4
4
4
4
3
4
3
422
/)(
;/)(
i
лплп
ii
i
лплn
ii
- динамические характеристики ТПП соответственно второго и четвертого
направлений;
лплплплп 24244242
/)(,/)(
- динамические характеристики пешеходных потоков для второго и четвер-
того направлений соответственно.
Принципы пропуска транспортных средств с маневрами налево и раз-
ворота для движения в обратном направлении. Возникающие задержки ав-
112
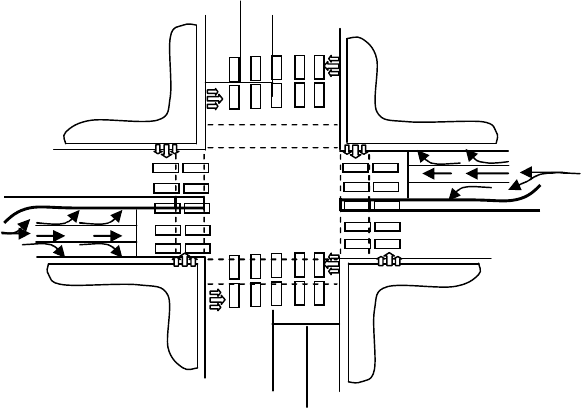
томобилей, движущихся прямо и направо за ТЕ, которые выполняют поворот
налево или разворот для движения в обратном направлении, можно не учи-
тывать. Во-первых, в стационарном процессе этот эпизод не скажется (отме-
ченные требования в [44, 45]); во-вторых, крайне редки такие перекрестки,
где нельзя объехать автомобиль, ожидающий возможности выполнить левый
поворот или разворот. Левый поворот или разворот могут выполняться толь-
ко при наличии свободного промежутка, т.е. временного разрыва, во встреч-
ном потоке, достаточного для осуществления этих маневров (см. рис. 2.7). В
последнем случае число автомобилей, стремящихся повернуть налево или
развернуться, ограничивается размерами площади, т.е. разделительной поло-
сы между встречными проезжими частями на перекрестке выделенной спе-
циально для этих целей, на которой могут разместиться автомобили, не
мешая движению прямо и направо в попутных потоках (рис. 2.8).
Следовательно, в уравнения (2.1), (2.2) – q и r должны добавиться ве-
личины U
mj
и U
cj
, определяющие вместимость накопительных проезжих час-
тей – площадей между проезжими частями встречных потоков и интенсив-
ность прибытия автомобилей с маневрами
43
,
jj
налево и разворота соответ-
ственно за цикл светофора.
Рис. 2.8 Схема выделения проезжей части для
левого поворота за счет разделительной полосы
113
Конкретные условия функционирования перекрестка, отличающиеся от
рассматриваемых, за счет определенных особенностей или ограничений
движения, могут потребовать добавочных соотношений в изложенной схеме
математического описания.
Рассмотрим в качестве примера автомобильный ряд на проезжей части
первого направления. В нем ТС, поворачивающие налево λ
3
j
и разворачи-
вающиеся λ
4
j
по причине пропуска встречных ТС сдерживают автомобили с
другими маневрами, стоящие позади в том же ряду. С точки зрения средних
оценок и случайности в индивидуальном смысле [44, 45] этот факт не требу-
ет дополнительных соотношений, так как затор в движении, созданный в
пределах цикла светофора, рассосется за последующие циклы.
Следовательно, величина U
mj
определяется статистически из наблюде-
ний, а так же по размерам накопительных проезжих полос, на которых могут
размещаться автомобили. Вторая величина – U
cj
определяется расчетным пу-
тем на основании статистических данных о λ
3
j
, λ
4
j
, а также о длительности
цикла светофора С.
Метод расчета длительностей циклов светофора. Принципы и логика
построения их расчетов. Если учесть, что доля зеленого такта для l-ой фазы α
l
изменяется (0 < α
l
< 1) и что красный такт для нечетных направлений одно-
временно является тактом для четных направлений, получим неравенства
)(
0
TCqC
l
и ))(1(
0
TCrC
l
.
К левым частям этих неравенств прибавим t
rl
и получим:
)(
0
TCqCt
lrl
и ))(1(
0
TCrCt
lrl
(2.3)
Величины t
rl
+qC и t
rl
+rC можно записать через уравнения (2.1) и (2.2):
4
1
1313
4
1
4
1
3
1
3
133
4
1
3131
4
3
4
3
3
3
3
311
/)(
;/)(
max
i
лплп
ii
i
лплп
ii
rl
СCC
СCC
qCt
114
4
1
2424
4
2
4
2
3
2
3
244
4
1
4242
4
4
4
4
3
4
3
422
/)(
;/)(
max
i
лплп
ii
i
лплп
ii
rl
СCC
СCC
qCt
Правые части равенств можно записать следующим образом:
4
1
2424
4
2
4
2
3
2
3
244
4
1
4242
4
4
4
4
3
4
3
422
/)()()()(
;/)()()()(
max
i
лплп
ii
i
лплп
ii
rl
СCCC
СCCC
qCt
где (λ
i
j
C) - число автомобилей, прибывших к стоп-линии за длительность
цикла С, ТЕ; (μ
jn
+μ
j+2л
) C - число пешеходов, прибывших к пешеходному пе-
реходу за длительность цикла С, пеш.; λ
i
j
Cτ
i
j
или (λ
i
j
C)τ
i
j
- время проезда
(λ
i
j
C) этого числа ТС, прибывших к перекрестку за время С, с. Это по сути
временная длина очереди (пачки) ТС, находящейся в начале движения пер-
вой и последней ее ТЕ.
Левые части равенств t
rl
+qC и t
rl
+rC определяют соответственно не-
четных и четных направлений максимальное время проезда автомобилей, ка-
кие могут прибыть к перекрестку за период цикла С.
Правые части – α
l
(C-T
0
) и (1-α
l
)(C-T
0
) представляют собой основной
разрешающий (зеленый) такт, в пределах которого очереди пропускаются
через перекресток; Т
о
– суммарная длительность промежуточных (желтых)
тактов (сигналов) цикла светофора, с. Отметим, что в среднем при стацио-
нарном потоке и при выполнении неравенств 0<α
l
<1, С>T
o
, q<1, r<1, q+r<1
перекресток будет функционировать нормально. Указанные неравенства ха-
рактеризуют условия движения, которым соответствует работа (пропуск по-
токов) перекрестка без накопления автомобилей у стоп-линии в последова-
4
1
1313
4
1
4
1
3
1
3
133
4
1
3131
4
3
4
3
3
3
3
311
/)()()()(
;/)()()()(
max
i
лплп
ii
i
лплп
ii
rl
СCCC
СCCC
qCt
115
тельных циклах. Накопление очереди автомобилей, которая может рассо-
саться за ряд последовательных циклов, но может и вырасти, означает нару-
шение неравенства и нормальной «работы» перекрестка. При этом
t
rl
+qC>α
l
(C-T
0
) и t
rl
+rC>(1-α
l
)(C-T
0
).
Кроме того, на левые части неравенств также оказывают значительное
влияние доли левых поворотов и разворотов в потоке
4
1
43
/
i
i
jjj
или
4
1
4433
/
i
i
j
i
jjjjj
на подходах к перекрестку, в частности на величины q и
r. При росте числа маневров, а значит и доли в q и r, вызывая адекватный
рост qC и rC, а также разности между левыми и правыми частями нера-
венств. Поэтому относительно возможного максимума левых поворотов и
разворотов на перекрестке должно выполняться неравенство
cjmj
UU , т.е.
cjmjjj
UUCC
43
, (2.4)
или
mjjj
UC )(
43
, где j = 1, 2, 3, 4.
Решение неравенств с левыми поворотами и разворотами позволяет
определить границы интенсивности движения ТС с указанными маневрами.
Иными словами, для всех направлений движения j = 1, 2, 3, 4 должно выпол-
няться неравенство:
43
/
jjmj
UC
. (2.5)
Если потребуется на конкретном перекрестке сократить время ликви-
дации микро затора, то этого можно достичь, например, созданием условий
для ожидания автомобилям с левыми поворотами и разворотами без помех
движению прямо и направо. Неравенство (2.4) позволяет определить длину
накопительной проезжей части для автомобилей с маневрами i = 3, 4. Техни-
чески оно реализуется различными путями, а математически это можно вы-
разить средней вместимостью накопительной проезжей части для автомоби-
лей с маневрами i = 3, 4. Для этого нужно знать величину U
mj
(2.4), опреде-
ляющую среднее число автомобилей, которые могут находиться на накопи-
тельной проезжей части – месте ожидания j-го направления (рис. 2.8).
116
Проведенный анализ подтверждает неотложную необходимость созда-
ния резервных зон для транспортных средств ожидающих левого поворота
или разворота в границах перекрестка как до, так и после стоп-линии при
U
cj
1.
Далее из соотношений (2.3), после некоторых преобразований, нахо-
дим экстремальность для q и r:
СtСTq
rll
//1
0
,
СtСTr
rll
//1)1(
0
(2.6)
а так как 0<α
l
<1, C>T
0
, то получим неравенства:
q<1, r<1. (2.7)
При сложении одноименных левых и правых частей неравенств (2.6) полу-
чим: q+r
СtСTСtСT
rllrll
//1)1(//1
00
. Преобразуя это неравен-
ство, найдем:
1/)2(1
0
СtTrq
rl
. (2.8)
Неравенство (2.8) будет соответствовать условиям движения, при ко-
торых СР обеспечивает нормальную “работу” перекрестка. При нарушении
этого неравенства, т.е. если q+r>
СtT
rl
/)2(1
0
перекресток нормально
функционировать не будет ввиду заторов на подходах к перекрестку. Заторы
могут быть ликвидированы увеличением длительности цикла светофора С,
путем перерасчета режимов светофорного регулирования на базе проведен-
ных результатов натурных наблюдений.
В неравенстве (2.8) подберем длительность цикла светофора С такую,
при которой (2.8) выражало бы верхний предел допустимого максимума и в
то же время сохранилась бы аналитическая модель (2.8)
q+r =
СtT
rl
/)2(1
0
, откуда определим С:
)1/(2
0
rqtTC
rl
. (2.9)
Равенство (2.9) является основной формулой определения оптимальной
длительности 2-фазных циклов светофора.
2.2.2 Методы определения длительностей основных разрешающего
(зеленого) и запрещающего (красного) тактов цикла светофора
117

Из неравенств (2.3) находим:
)/()(1)/(
00
TCrCtTCqCt
rllrl
(2.10)
Из уравнения (2.9) следует, что
СtTСtTCrq
rlrl
/)2(1/)2(
00
(2.11)
Откуда
qСtTr
rl
/)2(1
0
. (2.12)
Если проверить насколько равна правая часть уравнения (2.12) левой ее
части, то после нескольких преобразований (подстановки значения цикла С)
получим тождество r=r.
Далее, после подстановки в неравенство (2.10) значения величины r из
(2.12) получим:
),/()()/()(
00
TCqCtTCqCt
rlrl
т.е.
)/()(
0
TCqCt
rll
(2.13)
Можно α
l
определить и без С, для чего в равенство (2.13) подставить
значение цикла С из равенства (2.9):
0000
)1/()2(/)1/()2()/()( TrqtTrqtTqtTCqCt
rlrlrlrll
00
)(2/)1( TrqtqTrqt
rlrl
(2.14)
Долю разрешающего такта α
l
можно найти и более простым путем.
Поскольку сумма q+r представляет максимальную относительную величину
динамических характеристик ТП по нечетным и четным и четным направле-
ниям, то q/q+r будет означать какую долю q (величина нечетного направле-
ния) имеет в q+r или какую долю r имеет в q+r, но q/(q+r) + r/(q+r)=1
Таким образом из этих суждений вытекает, что
rq
q
l
для нечетных
направлений и
rq
r
l
для четных.
Но q
l
; r
l
. 10;10;10
rq .
Получение доли запрещающего (красного) такта β
l
для нечетных на-
правлений осуществляется аналогичным методом. Из равенства (2.11) нахо-
дим q
rСtTq
rl
/)2(1
0
(2.15)
118
После подстановки значения С в уравнение (2.15) получим тождество
q=q. Поскольку
β
l
+α
l
=(C-T
0
)/(C-T
0
), (2.16)
то
β
l
=1-α
l
. (2.17)
Подставив в равенство (2.17) значения α
l
из уравнения (2.13) и q из
уравнения (2.15), после преобразований получим β
l
.
)/()(
0
TCrCt
rll
(2.18)
или
00
)(2/)1( TrqtrTrqt
rlrll
(2.19)
Если для нечетных направлений α
l
будет долей основного разрешаю-
щего (зеленого) такта
,)/()(1)(2/)1()/()(
0000
TCrCtTrqtqTrqtTCqCt
rlrlrlrll
то для четных направлений эта доля будет являться долей основного запре-
щающего (красного) такта и наоборот, т.е.
.)/()(1
)(2/)1()/()(1
02
02020222
TCrCt
TrqtqTrqtTCqCt
r
rrr
(2.20)
Если доля красного такта β
1
для нечетных направлений будет:
,)(2/)1(
)/()()/(11
0101
010111
TrqtqTrqt
TCrCtTCqCt
rr
rr
то для четных направлений эта доля будет являться долей зеленого такта
,)(2/)1(
//11
0101
010122
TrqtrTrqt
TCqCtTCqCt
rr
rr
(2.21)
Из неравенств (2.3) правые части α
1
(С-Т
0
) и (1-α
1
)(С-Т
0
) в сумме дают
продолжительность основных (разрешающих и запрещающих) тактов
(α
1
+β
1
)(С-Т
0
), т.е. длительность цикла за вычетом суммарной длительности
промежуточных тактов C-T
0,
T
0
=T
1
0
+T
0
2
, и есть длительность основных так-
тов.
Продолжительность основных тактов находиться, в частности:
а) j = 1, 3:
119
1) длительность разрешающего такта l-фазы, t
зел.l
определится через
α
l
из (2.13)
)()(2/)1(
)()/()()(
000
000.
TCTrqtqTrqt
ТCTCqCtTCt
rlrl
rlllзел
(2.22)
2) длительность запрещающего такта t
кр.l
определяется через (2.13),
(2.18), (2.19)
)(/1))(1()(
00010
TCTCqCtTCTCt
rllкрl
).()(2/)1(
)(/
000
000
TCTrqtrTqrtrCt
TCTCrCtqCtTC
rlrlrl
rlrl
(2.23)
б) j = 2, 4:
1)
)(/1))(1()(
0001012.
TCTCqCtTCTCtt
rlкрзел
)()(2/)1(
)(/
000
000
TCTrqtrTqrtrCt
TCTCrCtqCtTC
rlrlrl
rlrl
. (2.24)
2)
qCtTCqCtTCTCtt
rlrlзелкр 00011.2
/)()(
.
.))(/1(
))(1()()(2/)1(
000
02000
rCtTCTCTCrCt
TCTCTrqtqTrqt
rr
rr
(2.25)
Следует отметить, что
rq 10
rq 1
. При двухфазном
цикле СР
00
2 TCTCrCqCt
rl
.
При трехфазном цикле СР
00
3 TCTCsCrCqCt
rl
,
поскольку 1
. Где α, β
j
и δ
j
это доли соответственно разрешающих и
запрещающих тактов, их сумма
умноженная на (С-Т
0
) есть сум-
марная длительность промежуточных тактов Т
0
в трехфазном цикле С свето-
фора.
Таким образом, по формулам (2.10)-(2.18) определяются рациональные
доли и длительности основных рабочих тактов l-х фаз циклов СР для направ-
лений движения j = 1, 2, 3, 4 через перекресток.
2.2.3 Метод и логика расчета и расценки длительностей промежу-
точных тактов цикла светофорного регулирования
120
