Жариков В.А. Основы физической геохимии
Подождите немного. Документ загружается.


и некоторой величине свободной энергии, возникающей в растворе за счет отклонения от
идеальности. Последнюю функцию обозначают термином "избыточная свободная
энергия", она равна:
Свободная энергия смешения неидеального раствора определится соотношением
или
Симметричным образом для характеристики отклонения растворов от идеальности
введены другие избыточные термодинамические функции.
Энтропия раствора
где S
I
- энтропия идеального раствора; S
E
- избыточная энтропия. Энтальпия раствора
Объем раствора
где - избыточные энтальпии и объем, а - соответствующие функции
смешения неидеальных растворов.
Наконец, для полной симметрии обозначим как избыточный химический потенциал член
RTlnγ
i
в выражении (2.162) химического потенциала неидеального раствора, т. е.
μ
i
E
= RTlnγ
i
,
(2.175)
и
μ
i
= μ
i
E
+ μ
i
I
= μ
i
0
+ RTlnγ
i
+ RTlnx
i
,
(2.176)
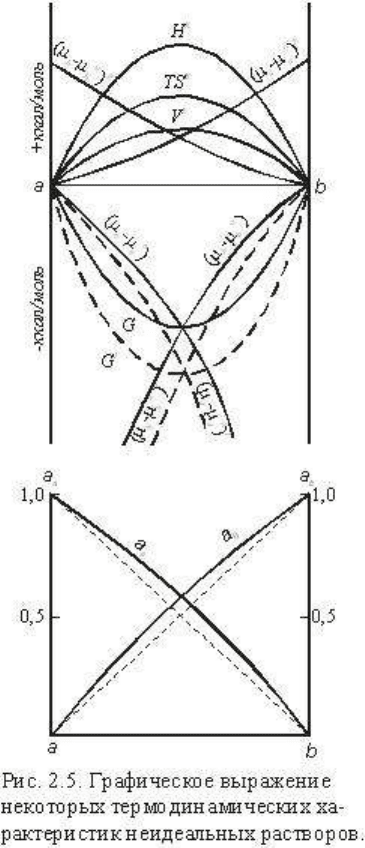
Для более наглядной характеристики избыточных термодинамических функций, их связи
с активностями компонентов на рис. 2.5 представлены некоторые типичные соотношения
для бинарного раствора, который характеризуется положительными отклонениями от
идеальности с соотношениями H
E
> TS
E
> G
E
и приблизительно симметричными
графиками этих функций. Отметим, что отклонения могут быть и отрицательными, и
знакопеременными для всех избыточных функций. Однако при этом кривая зависимости
G = G
E
+ G
I
от активности компонентов всегда будет вогнутой (вниз), а кривая
зависимости S = S
E
+ S
I
выпуклой (вверх), так как в противном случае раствор будет
распадаться на механическую cмесь в области составов, где термодинамический
потенциал раствора окажется больше, а энтропия меньше, чем у механической смеси
Уравнение смещенного равновесия и вытекающие из него законы
Рассмотрим изотермо-изобарическую систему с вполне подвижными компонентами.
Обозначим через I и II два каких-либо состояния системы. Эти состояния будут
находиться в равновесии, если G
I
m
= G
II
m
, так как в противном случае система
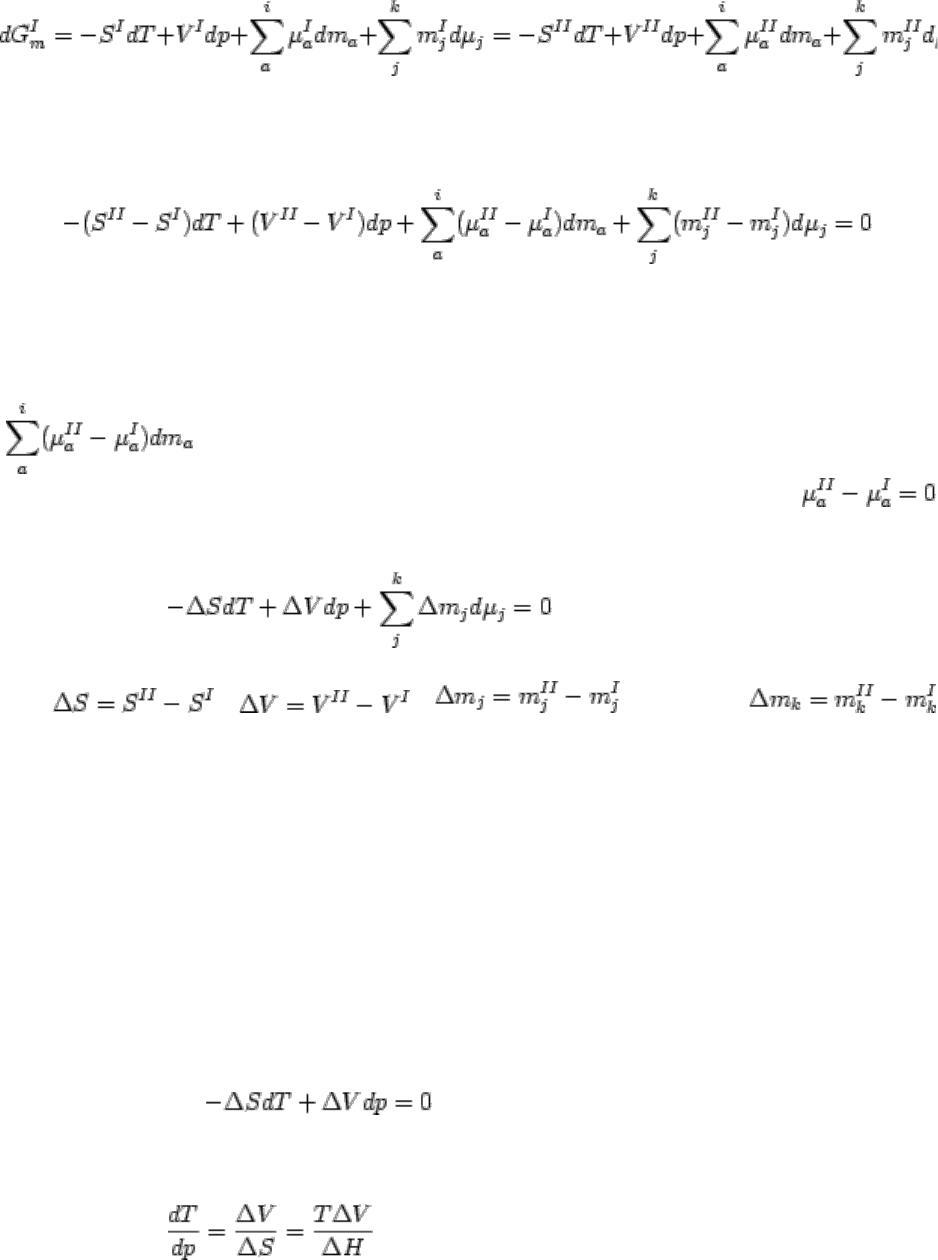
самопроизвольно переходила бы в состояние с меньшей свободной энергией. Если мы
будем изменять факторы состояния, то равновесие сохранится, если dG
I
m
= dG
II
m
, или,
раскрывая значения свободной энергии:
.
Сгруппируем члены:
.
В этом выражении член
равны нулю, так как в условиях равновесия химические потенциалы
компонентов для различных частей или состояния системы равны, а поэтому
. В результате имеем
,
(2.177)
где , , и так до
изменение энтропии, объема и масс компонентов при переходе из одного равновесного
состояния в другое. Уравнение (2.177) носит название уравнения (пpинципa)
смещенного равновесия: оно показывает связь между изменениями интенсивных и
экстенсивных параметров, существующую в равновесной системе при изменении
факторов состояния. Уравнение смещенного равновесия представляет фундаментальную
характеристику фазовых соотношений. Из уравнения как частные следствия вытекают
многие важные термодинамические законы и уравнения, такие, например, как уравнение
Клаузиуса-Клапейрона, закон действующих масс и т. д. Рассмотрим некоторые следствия.
Ограничимся условиями постоянства химических потенциалов вполне подвижных
компонентов, т. е. dμ
j
= ... = dμ
k
= 0, тогда уравнение (2.177) сведется к следующему:
,
откуда
,
(2.178)
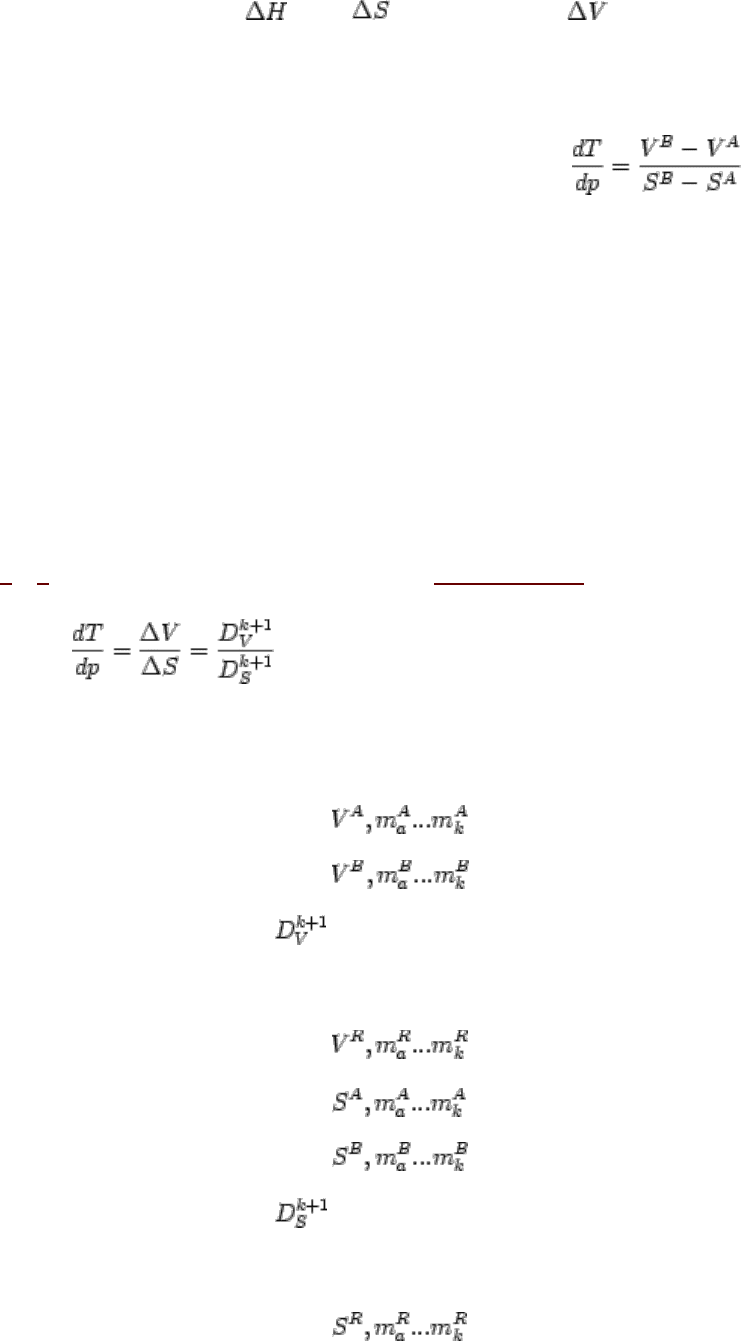
Уравнение (2.178) носит название уравнения Клаузиуса-Клапейрона. Оно показывает
взаимосвязь между тепловым ( или ) и объемным ( ) эффектами реакции
перехода системы из одного состояния в другое и значениями соответствующих
интенсивных параметров системы - температуры и давления.
Для однокомпонентной системы это разница между энтропиями и объемами двух фаз
(например А и В) для моновариантной реакции A=B, т. е. , которая
изобразится моновариантной линией на диаграмме с координатами Т и р. В
двухкомпонентной системе уравнение Клаузиуса-Клапейрона будет описывать
трехфазовую моновариантную реакцию, отвечающую соответствующей моновариантной
линии на Т-р диаграмме и так до систем с k компонентами, где в моновариантном (n=1)
равновесии находятся r=k+1 фаз.
Во всех случаях когда число компонентов больше одного в уравнении Клаузиуса-
Клайперона ΔS и ΔV представляет изменение энтропии и объема всей системы и для
многофазовой реакции должны быть учтены массы реагирующих фаз и баланс слагающих
их компонентов. Обычно для этого используются уравнения Гиббса-Дюгема,
характеризующих каждую фазу и сумма этих однородных линейных уравнений решают
методом детерминант (определителей). Отсылая читателя за подробным выводом к
углубленным курсам термодинамики и нижеследующим разделам книги (см. разделы
главы III 4 и 6), приведем здесь итоговую формулу в общем виде7
,
(2.178)
для k компонентной системы и моновариантного равновесия r = k + 1 фаз. В уравнении
(2.179) детерминанты равны
...
...
...
...
Заметим, что если мы имеем дело с фазами переменного состава, оказывается удобным
матрицы и составлять
в мольных долях компонентов.
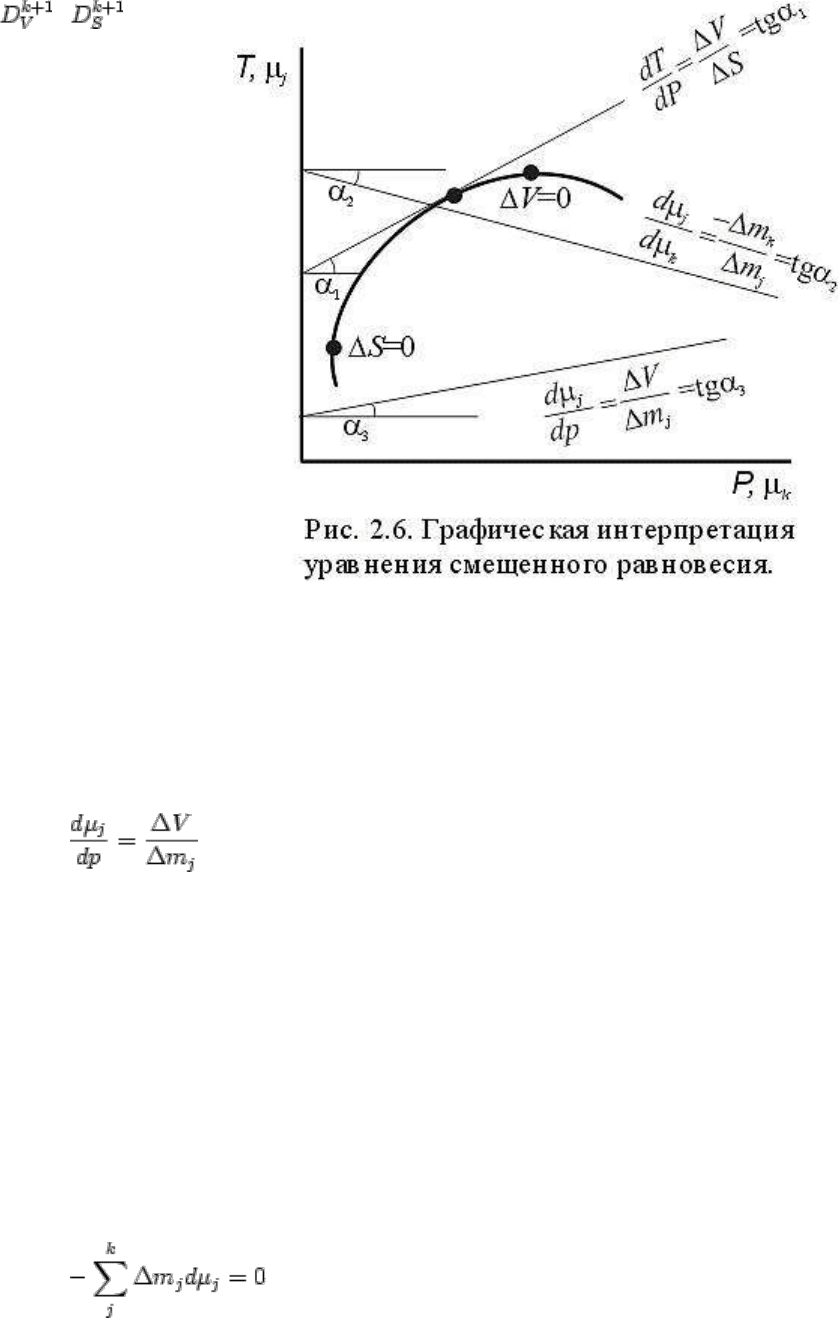
Рассмотренные соотношения
имеют наглядную и широко
используемую в физико-
химическом анализе
графическую интерпретацию.
На рисунке 2.6, где по оси
ординат отложена температура,
а по оси абсцисс - давление,
dT/dp представляет собой
тангенс угла наклона
касательных к моновариантным
линиям, ограничивающим два
каких-либо состояния системы
и находящимся в равновесии на
этой моновариантной линии.
Интегрируя (2.178) и (2.179) -
∫ΔSdT + ∫ΔVdp = const получим
уравнения соответствующих моновариантных линий. Отметим, что интегрирование
уравнение Клаузиуса-Клапейрона, представляет нелегкую задачу (в связи с зависимостью
ΔS от Т и ΔV от p), которую мы рассмотрим в дальнейшем, в специальной главе.
Зададимся теперь условиями, когда температура и химические потенциалы всех вполне
подвижных компонентов, кроме компонента j, постоянны, т. е. dT = 0, dμ
j+1
= ... = dμ
k
= 0
тогда ΔVdp - Δm
j
dμ
j
= 0, откуда
,
(2.180)
Уравнение (2.180) показывает связь между объемным эффектом реакции и изменением
содержания вполне подвижного компонента, существующую в системе при равновесном
переходе от одного состояния в другое при изменении интенсивных факторов состояния -
давления и химического потенциала вполне подвижного компонента. На диаграмме в
координатах μ
j
- p (см. фиг.2.6) уравнение (2.180) выражает тангенс угла наклона
касательной к моновариантной k+1 фазовой линии, а интеграл -∫Δm
j
dμ
j
+ ∫ΔVdp = const
описывает уравнения моновариантных линий в координатах μ
j
- p.
Наконец, рассмотрим условия, когда температура и давление постоянны, т. е. dT=0; dp=0.
Тогда уравнение (2.177) предстанет в виде
,
(2.181)
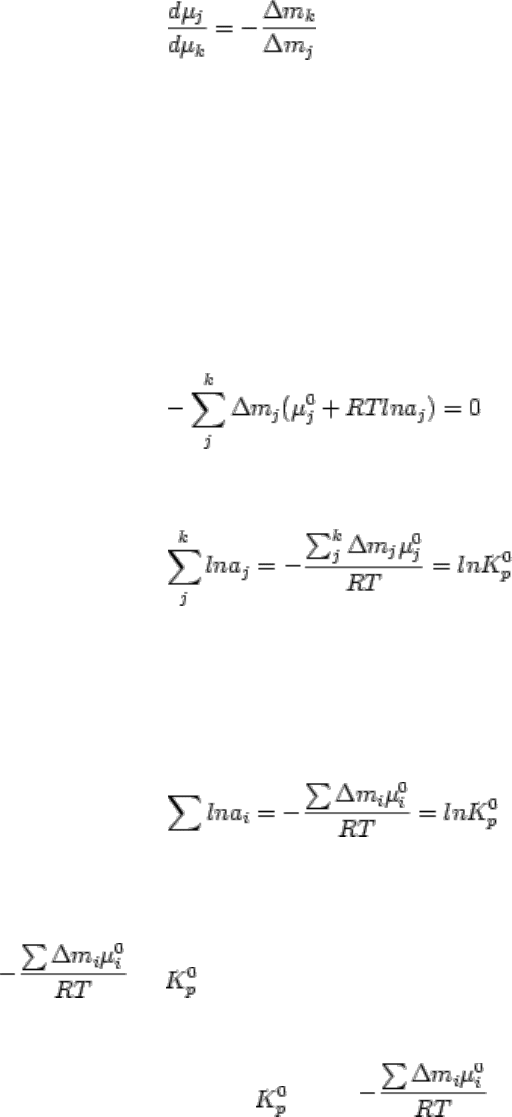
Соотношение (2.181) является одной из форм выражения закона действующих масс,
который устанавливает зависимость между изменениями масс и химических потенциалов
или активностей компонентов для соответствующих равновесных состояний системы.
Например, в системе, где изменяются химические потенциалы только двух компонентов,
зависимость
(2.182)
также характеризует тангенс угла наклона касательной, а интеграл -∫Δm
j
dμ
j
- ∫Δm
k
dμ
k
=
const представляет уравнение моновариантной линии на диаграмме μ
j
-μ
k
(см. рис. 2.6).
Придадим выражению закона действующих масс более обычную форму. Для этого нам
необходимо проинтегрировать уравнение (2.181). Это можно сделать непосредственно,
полагая, что массы компонентов не зависят от их химических потенциалов, и определив
пределы интегрирования, но проще вспомнить, что интегральное выражение химического
потенциала (уравнение (2.154)) равно μ
j
= μ
j
0
+ RTlna
j
. Тогда (2.181) при интегрировании
превращается в следующее уравнение
(2.183)
Откуда путем несложных преобразований выводится соотношение
(2.184)
которое и представляет закон действующих масс в раскрытой логарифмической форме.
Поскольку уравнение справедливо для любого числа реагирующих компoнентов, пределы
суммирования в выражении (2.184) обычно опускаются, а компонент обозначается любой
буквой, например i:
(2.184)
Потенциируя уравнение (2.184) получим в левой части произведение активностей
компонентов, которое обычно обозначается как ∏a
i
Δm
i
, а в правой части - величину exp (
) = , которая является постоянной при данных температуре и давлении и
называется константой равновесия реакции. В результате получим
∏a
i
Δm
i
= = exp ( )
(2.185)
обычную нелогарифмическую форму записи уравнения закона действующих масс.
Обратим внимание на то, что во всех формулах (2.181) - (2.184) и ниже компоненты
выражены алгебраической суммой или произведением активностей (2.185). Реальные

знаки Δm
j
...Δm
k
зависят от уравнения соответствующих реакции и способа их записи (как
процессов, происходящих внутри системы или вызванных внешним воздействием в.п.к.).
Закон действующих масс является главным термодинамическим соотношением,
описывающим зависимость химических равновесий в системе. Рассмотрим подробнее
некоторые существенные аспекты закона действующих масс.
Установим прежде всего важную термодинамическую зависимость, связывающую
константу равновесия с изменением изотермо-изобарического потенциала
соответствующей реакции. Как было показано выше (уравнения (2.150), (2.167) и др.),
изотермо-изобарический потенциал может быть представлен в виде
где . Сравнивая два равновесных состояния системы А и В, получим:
или
Но из (2.184)
тогда окончательно получим
(2.186)
Уравнение (2.186) показывает, что константа равновесия определяется величиной
изобарно-изотермического потенциала реакции. Оно служит для расчета констант
равновесия реакций.
Наконец, уравнение (2.184) можно преобразовать, выражая в явной форме избыточные
функции неидеальных растворов. Сопоставляя рассмотренные термодинамические
зависимости, можно вывести следующие соотношения:
или
(2.187)
и, наконец,
(2.188)

где K
p
E
- "избыточная" константа реакции, связанная с отклонением растворов от
идеальности, равная K
p
E
= exp ( ) или ln K
p
E
= . Уравнение (2.188)
может быть представлено и в нелогарифмической форме.
∏x
i
Δm
i
= K
p
0
.
K
p
E
= K
p
(2.189)
Выразим константу равновесия неидеального раствора через стандартную и избыточную
свободную энергию. Опуская подробные выкладки, сделанные нами выше из
сопоставления уравнений (2.186), (2.187) и (2.188) легко вывести следующее уравнение
RT ln K
p
= - (ΔG
0
+ ΔG
E
).
(2.190)
Рассмотрим еще два важных соотношения, показывающих зависимость константы
равновесия реакции от температуры и давления. Проще всего это сделать следующим
образом. В соответствии с рассмотренными зависимостями можно записать:
и уравнение смещенного равновесия предстанет в виде:
-ΔSdT + ΔVdp + RT dln K
p
0
= 0
(2.191)
Из уравнения (2.191) непосредственно следуют уравнение изобары реакции (уравнение
Вант-Гоффа), показывающее зависимость константы равновесия от температуры:
(2.192)
и уравнение изотермы реакции, показывающее зависимость константы равновесия от
давления:
(2.193)
Таким образом, во всех приведенных выражениях закона действующих масс фигурирует
термодинамическая константа равновесия, записанная через активности и мольные доли
компонентов. При расчетах нередко удобнее выразить количества компонентов в виде
мольных масс (количествах молей) или в объемных концентрациях. Тогда для идеальных
растворов "мольная" константа K
m
будет равна
K
m
= ∏(m
i
)
Δm
i
,
(2.194)
а концентрационная (K
c
):
K
c
= ∏(C
i
)
Δm
i
,
(2.194)

где под знаком П, как и выше стоят алгебраические произведения мольных масс или
концентраций.
Естественно, что K
p
, K
m
, K
c
имеют различное значение (если ∑Δm
i
не равно нулю).
Соотношения между константами (которые выводятся подстановками x
i
= m
i
/ ∑m и C
i
=
m
i
/ V, что мы опускаем) следующие:
В случае ∑Δm
i
= 0, т. е. реакция не сопровождается изменением числа молей, значения
констант совпадают.
Для газовых смесей закон действующих масс можно выразить через парциальные
давления:
Отметим, что собственно для газовых смесей закон действующих масс был и
сформулирован впервые исходя из молекулярно-кинетических соображений, и уже
позднее получил полное термодинамическое истолкование.
5. ОСНОВНЫЕ ПОНЯТИЯ И ПРИНЦИПЫ ТЕРМОДИНАМИКИ НЕОБРАТИМЫХ
ПРОЦЕССОВ
Как уже подчеркивалось, природные процессы представляют неразрывное сочетание
равновесных состояний с общим необратимым течением процессов. Естественным
поэтому выглядит стремление распространить термодинамический аппарат на описание и
исследование кинетики и динамики природных процессов, т. е. всех тех явлений, которые
вызывают необратимые изменения природных систем. Такой общий подход оказывается
возможным благодаря развитию методов термодинамики неравновесных, точнее,
необратимых процессов. В этом разделе рассмотрим основные понятия и принципы
термодинамики необратимых процессов, необходимые для использования в дальнейшем
методов необратимой термодинамики при анализе кинетики и динамики природных
процессов минералообразования.
Термодинамика необратимых процессов базируется на обобщении классической
термодинамики и новых принципов, отражающих главные феноменологические законы
необратимых изменений систем. Главными законами необратимой термодинамики
являются: уравнения возрастания и скорости возрастания энтропии; закон линейных
соотношений потоков и сил; принцип взаимности; закон линейной скорости возрастания
энтропии при стационарных состояниях. Рассмотрим эти главные соотношения.

Энтропия и термодинамические принципы необратимых процессов
При выводе уравнений термодинамических потенциалов во всех уравнениях
присутствовал член δQ
i
, обозначенный как <некомпенсированное тепло> и выражающий
возрастание энтропии или уменьшение термодинамического потенциала при необратимом
стремлении системы к равновесию. Обозначив
δQ
i
= Td
i
S,
(2.201)
для необратимого процесса, целесообразно отметить обратимый теплообмен системы с
окружающей средой как
δQ
e
= Td
e
S,
(2.202)
Заметим, что δQ
i
всегда величина положительная, тогда как знак δQ
e
зависит от
направления потока тепла. Суммарная тепловая работа δQ = δQ
e
- δQ
i
, откуда видно, что
δQ = δQ
e
= max только когда δQ
i
= 0. Обычно δQ < δQ
e
поскольку δQ
i
> 0. Иначе говоря
теплообмен системы с окружающей средой максимален при обратимых процессах и
всегда меньше при необратимых вследствие расхода части тепла на естественное
необратимое возрастание энтропии.
Как было показано выше, изменение внутренней энергии
dU = δQ + δA + δW - δQ
i
,
Введя дополнительные обозначения δQ
e
, δA
e
, δW
e
для обратимых процессов и преобразуя,
получим:
(2.203)
Нетрудно убедиться, что заключенная в скобки часть уравнения (2.203) представляет
обобщенное выражение термодинамического потенциала системы, точнее, той его части,
которая изменяется (уменьшается) в результате необратимых процессов в системе при
постоянных факторах состояния. В зависимости от термодинамического типа системы,
т.e. от набора факторов состояния, это выражение можно раскрыть через уравнение
термодинамического потенциала соответствующей системы.
Изохоро-изоэнтропическая система U=ƒ(S,V,m
a
,...,m
k
) при постоянстве факторов
состояния характеризуется отсутствием обратимого обмена с окружающей средой теплом,
механической и химической работой. Для такой изохоро-изоэнтропической системы
δQ
e
=0, δA
e
=0, δW
e
=0 и, обозначив через d
i
U изменение внутренней энергии, вследствие
необратимых процессов из (2.203) получим
(2.203)
