Жариков В.А. Основы физической геохимии
Подождите немного. Документ загружается.

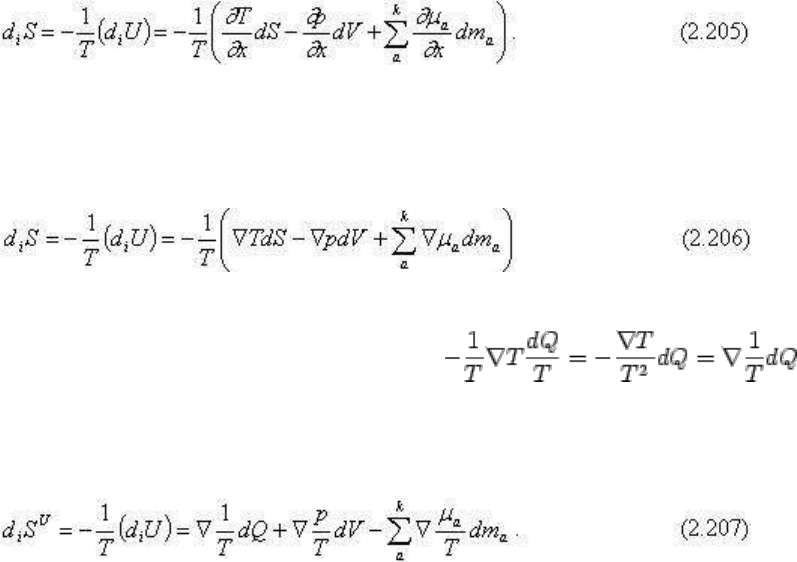
Это уравнение выражает изменение необратимой энтропии через изменение внутренней
энергии, представляющей термодинамический потенциал изохоро-изоэнтропической
системы. Необратимая энтропия возрастает при всех необратимых процессах,
протекающих с уменьшением внутренней энергии.
Как было показано выше, уменьшение термодинамического потенциала системы при
постоянных факторах состояния происходит путем изменения (выравнивания по фазам)
интенсивных параметров системы, сопряженных с экстенсивными факторами состояния.
В изохоро-изоэнтропической системе, где возможно неравенство по фазам или частям
системы температур, давлений и химических потенциалов компонентов, уменьшение
внутренней энергии происходит за счет потоков тепла от более нагретых частей системы к
менее нагретым, потоков вещества из частей с более высокими химическими
потенциалами, перемещение вещества вследствие разностей в давлении. Необходимым
условием потоков является существование градиентов соответствующих интенсивных
параметров.
Как было показано выше, уменьшение термодинамического потенциала системы при
постоянных факторах состояния происходит путем изменения (выравнивания по фазам)
интенсивных параметров системы, сопряженных с экстенсивными факторами состояния.
В изохоро-изоэнтропической системе, где возможно неравенство по фазам или частям
системы температур, давлений и химических потенциалов компонентов, уменьшение
внутренней энергии происходит за счет потоков тепла от более нагретых частей системы к
менее нагретым, потоков вещества из частей с более высокими химическими
потенциалами, перемещение вещества вследствие разностей в давлении. Необходимым
условием потоков является существование градиентов соответствующих интенсивных
параметров.
Иногда для одномерного (х) пространства, где градиенты ∂T/∂x, ∂p/∂x и ∂μ/∂x,
возрастание энтропии, или уменьшение термодинамического потенциала, выразится
уравнением:
Для многомерной непрерывной системы градиенты интенсивных параметров в общем
случае многомерны и выражаются обычно через оператор Гамильтона (∇T = grad
x,y,z
T и т.
д.).
Придадим уравнению (2.206) общий вид. Для этого: 1) заменим dS на dQ/T и
соответственно первый член представим ; 2) внесем -
{{1} \over {T}} под знак оператора в других членах; 3) обозначим необратимую энтропию
символом U, отмечая ее принадлежность к изохоро-изоэнтропической системе.
Окончательно получим:
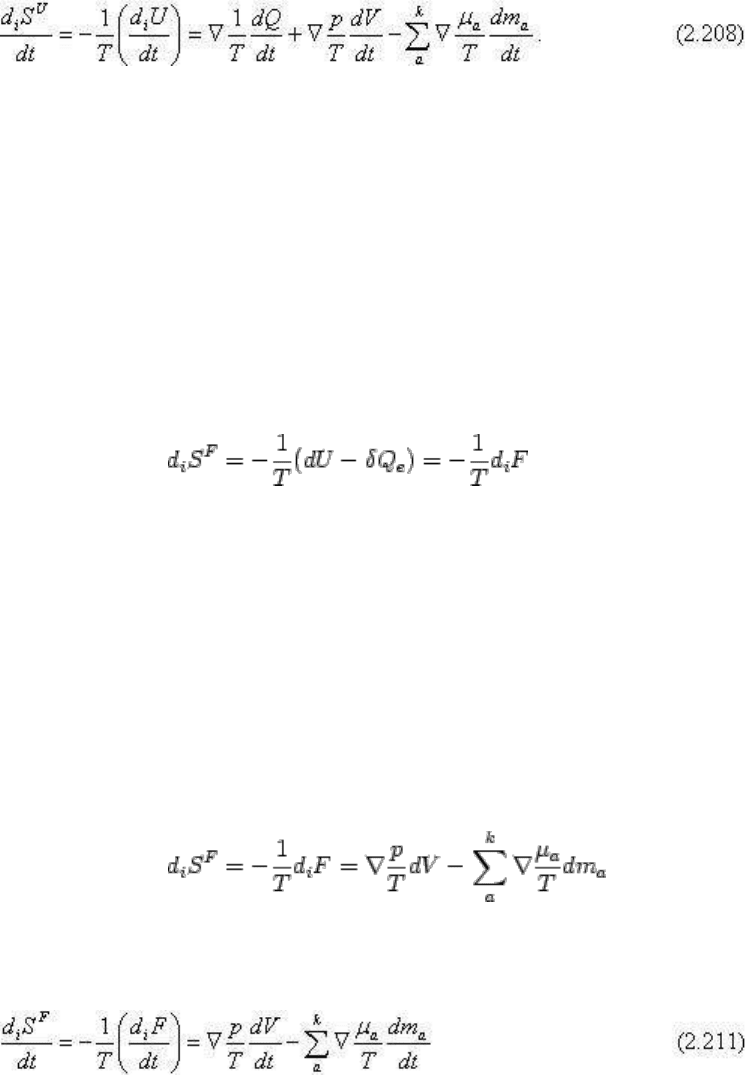
Это уравнение носит название уравнения возрастания (или производства) энтропии и
является одним из основных в необратимой термодинамике. Вывод его ясно выражает
принципиальную связь равновесной и необратимой термодинамики.
Возьмем от уравнения (2.207) производную по времени, полагая, что градиенты от него не
зависят, а являются функциями пространства. В результате получим уравнение скорости
возрастания или скорости производства энтропии:
Выражение (2.208) представляет фундаментальное уравнение термодинамики
необратимых процессов, выражающее скорость возрастания энтропии через изменение
внутренней энергии и канонических параметров термодинамических систем.
Раскроем теперь через термодинамические потенциалы возрастание энтропии для других
типов термодинамических систем. В изохоро-изотермической системе F=ƒ(T, V, m
a
,...,
m
k
), при постоянстве факторов состояния, могут происходить процессы обратимого
теплообмена с окружающей средой, т. е. δQ
e
≠ 0, тогда как изменение механической и
химической энергии происходит вследствие необратимых процессов, т. е. δA
e
=0, δW
e
=0.
Уравнение изменения необратимой энтропии для этой системы выразится как
(2.203)
показывая, что возрастание необратимой энтропии происходит вследствие необратимого
уменьшения свободной энергии (d
i
F), представляющей термодинамический потенциал
этой системы.
Уравнение (2.209) можно раскрыть различными способами. Но в основе их лежит
одинаковый физический смысл, отражающий то, что в изотермической системе не могут
происходить необратимые процессы переноса тепла, но могут осуществляться таковые за
счет разности (градиентов) давлений и химических потенциалов. Тогда повторяя
проделанные выше операции, но уже для изотермо-изохорической системы, получим для
многокомпонентной непрерывной системы
(2.209)
- уравнение возрастания энтропии, а взяв производную по времени, полагая градиенты от
него независимыми, получим:
По-видимому, не требует особых пояснений дальнейшее распространение симметричных
преобразований на другие канонические типы термодинамических систем. Приведем
соответствующие выражения через термодинамические потенциалы для уравнений
возрастания и скорости возрастания энтропии.

Для системы H = ƒ(S, p, m
a
,..., m
k
):
Для системы G = ƒ(T, p, m
a
,..., m
k
):
К термодинамическим системам с вполне подвижными компонентами, как было показано
выше, относятся такие системы, в число факторов состояния которых входят химические
потенциалы вполне подвижных компонентов. Такие системы являются
изопотенциальными, для них возможны обратимые процессы обмена с окружающей
средой массами вполне подвижных компонентов. Естественно, что при постоянстве
факторов состояния необратимая энтропия не может возрастать за счет химической
энергии вполне подвижных компонентов и соответствующий член должен быть
изъят из уравнений, характеризующих необратимые процессы в системах. Запишем это в
общем виде:
где d
i
S
Ф
m
- возрастание энтропии в системе с в.п.к., Ф - любой термодинамический
потенциал обычной системы, Ф
m
- любой термодинамический потенциал системы с в.п.к..
Скорость возрастания энтропии выразится как
(2.217)
Проведя необходимые преобразования (мы опускаем их ввиду полной идентичности с
проведенными выше), получим систему уравнений возрастания и скорости возрастания
энтропии, выраженную через термодинамические потенциалы для систем с вполне
подвижными компонентами.

Выведенные здесь и выше уравнения возрастания (<производства>) и скорости
возрастания энтропии, выраженные через уменьшение и скорости уменьшения
термодинамических потенциалов, представляют характеристические уравнения
необратимых процессов в простых термодинамических системах, включая системы с
вполне подвижными компонентами. Эти уравнения показывают зависимость приращения
и скорости приращения энтропии от изменения канонических термодинамических
параметров системы.
Следует заметить, что характеристика необратимых процессов через изменение
термодинамического потенциала системы имеет определенные преимущества. Они
обусловлены тем, что термодинамический потенциал всегда представляет
характеристическую функцию системы, тогда как описание необратимых изменений через
возрастание энтропии для определенных систем в известной мере искусственно. Так, при
необратимых процессах в изоэнтропических системах энтропия их (при постоянстве
факторов состояния) остается, конечно, постоянной, но происходит уменьшение
внутренней энергии за счет рассеяния ее во внешнюю среду, т.е. происходит увеличение
d
i
S за счет уменьшения d
e
S.
Заметим также, что причины вызывающие необратимые процессы, или, как принято их
обозначать, - действующие силы, не просто градиенты интенсивных параметров, а ∇(1/T),
∇(p/T), ∇(μ/T). Это имеет существенное значение для правильного понимания и описания
неизотермических процессов, отражая определенный доминант температуры перед
другими интенсивными параметрами8. Естественно, что для изотермических процессов и
систем температура как постоянная величина может быть вынесена за знак градиентов.
При этом необратимые изменения в системе непосредственно равны уменьшению
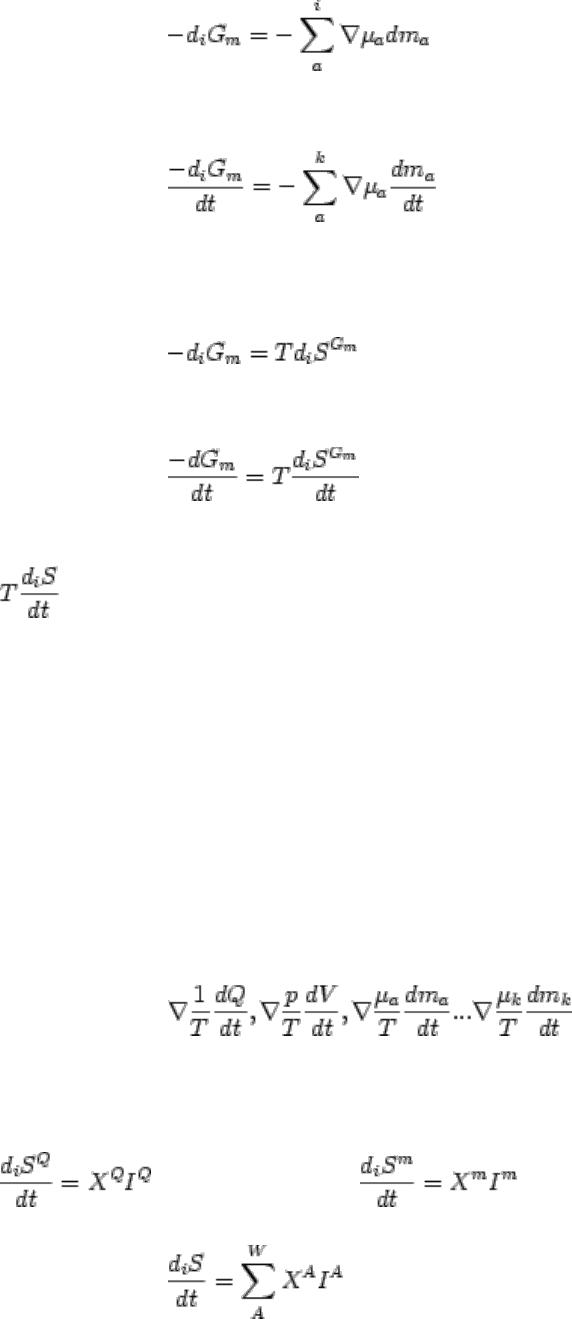
термодинамического потенциала. Вынося T за знак градиента, вместо (2.224) и (2.225),
например, получим:
(2.226)
и
(2.226)
Сопоставляя (2.224, 2.225) и (2.226, 2.227) можно видеть, что в последнем случае
(2.228)
и
.
(2.229)
Отметим, что такой способ задания производства энтропии Td
i
S и скорости ее возрастания
широко используется в работах по необратимой термодинамике, нередко без
объяснения предпочтительности выбора. В свете изложенного представляется
правильным использовать последние выражения (2.228, 2.229) во всех случаях
изотермических процессов, но при наличии температурных градиентов и тепловых
потоков всегда применять более общие выражения действующих сил: ∇(1/T), ∇(p/T),
∇(μ/T).
Выведем еще одно основополагающее соотношение термодинамики необратимых
процессов. Обратим внимание на то, что во всех уравнениях скорости возрастания
энтропии (или уменьшения термодинамического потенциала) члены, выражающие
перенос тепла, изменение объема, перенос вещества, представлены произведениями вида:
действующая сила x количество тепла (вещества) в единицу времени:
.
(2.229)
Тогда, обозначив действующие силы через Х, а количество экстенсивной величины (Q, V,
m) в единицу времени через потоки - I
Q
, I
V
, I
m
и т. д. получим для теплопереноса
, для массопереноса и т. д. и в общем виде:
.
(2.230)
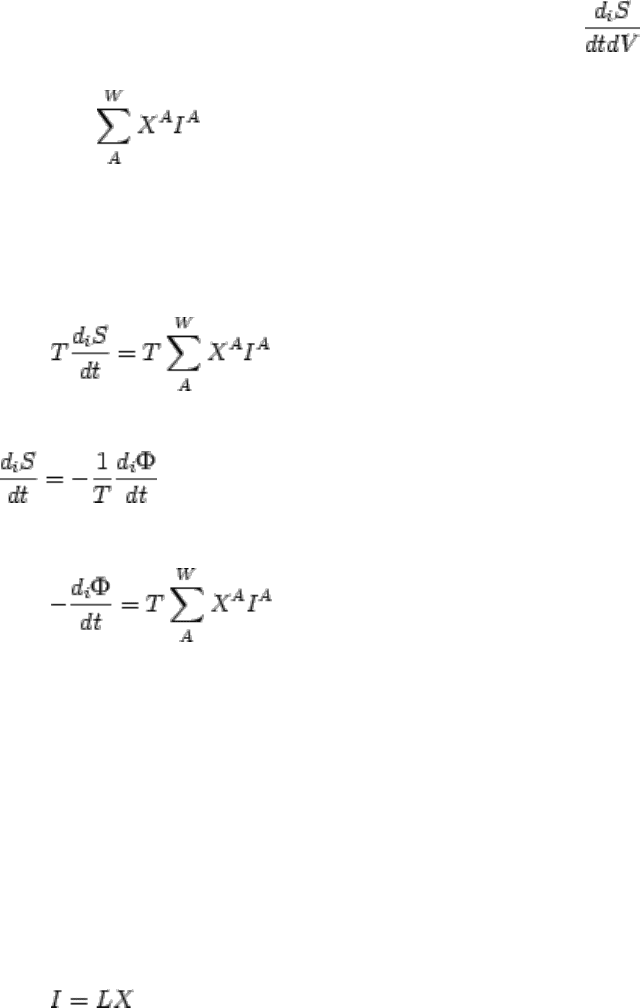
Это фундаментальное соотношение необратимой термодинамики связывает скорость
производства энтропии с действующими потоками и силами. Оно показывает, что
скорость возрастания энтропии пропорциональна произведению действующий силы на
поток и в случае действия нескольких потоков они суммируются, давая общую скорость
возрастания энтропии в системе.
Уравнение (2.230) иногда записывается в удельных параметрах ζ
v
= , где
ζ
v
= .
(2.231)
- скорость возрастания энтропии в единице объема.
Распространена также запись основного уравнения и в виде:
.
(2.232)
Поскольку нетрудно видеть, что в этом случае произведение действующих
сил на потоки равно скорости уменьшения термодинамического потенциала
.
(2.233)
Преимущества такой записи, особенно для изотермических процессов несомненна.
Закон линейных соотношений и принцип взаимности
Закон линейных соотношений устанавливает линейную зависимость любого потока
(потока тепла, потока вещества и т. д.) от вызывающих его действующих сил (от
градиента температуры, градиентов химических потенциалов и т. д.). Если обозначить
поток через I, а действующую силу через Х, то закон линейных соотношений запишется
как
.
(2.234)
где L - коэффициент пропорциональности, называемый кинетическим коэффициентом,
или феноменологическим коэффициентом, или коэффициентом переноса. Последнее
наименование более точно выражает физическую сущность: L представляет удельное
количество экстенсивной характеристики процесса переноса действующей силою через
единичное пространство (объем, сечение и т.). Так для диффузии компонента a:
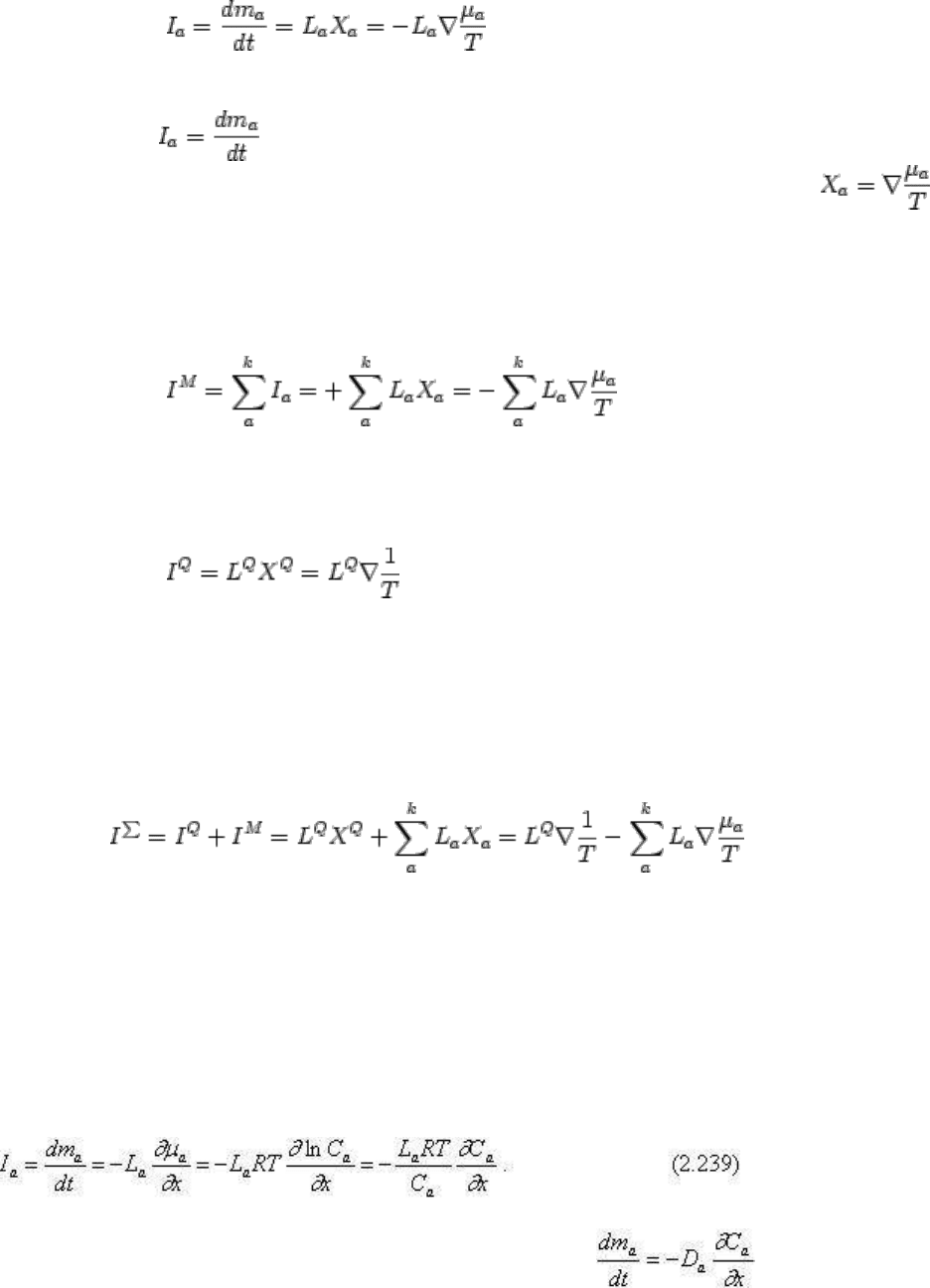
.
(2.235)
где, очевидно, - поток компонента a, L
a
- коэффициент переноса - количество
вещества а, переносимого через единичное пространство под влиянием
действующей силы диффузии. Если диффундирует несколько компонентов и
действующие силы выражены как в (2.235) в соответствии в уравнением скорости
возрастания энтропии (см. уравнения 2.208-2.225), то общий поток вещества будет равен
сумме потоков остальных компонентов:
.
(2.236)
Аналогично для потока тепла (I
Q
) будем иметь:
.
(2.237)
Закон линейных соотношений устанавливает также, что в системе, где осуществляется
несколько потоков (тепла, вещества и т. д.), они могут быть сложены, если действующие
силы выражены в соответствии с уравнением скорости возрастания энтропии. Итак, если в
системе происходит перенос тепла и вещества, то общий поток равен:
.
(2.238)
Обратим внимание, что во всех уравнениях (2.235-2.238) коэффициенты переноса не
зависят от действующих сил (условие линейности), тогда как обычные коэффициенты
диффузии, теплопроводности имеют сложный нелинейный характер. Покажем это на
простом примере изотермической одномерной диффузии, используя <концентрационное>
выражение химического потенциала. Диффузионный поток компонента а в этом случае
выразится как
Сравнивая это выражение с известным уравнением Фика: нетрудно видеть,
что D
a
= L
a
RT / C
a
(или L
a
= D
a
C
a
/ RT) и сколь сложна природа обычного коэффициента
диффузии. Еще более сложные соотношения при неизотермической диффузии
рассмотрим ниже.
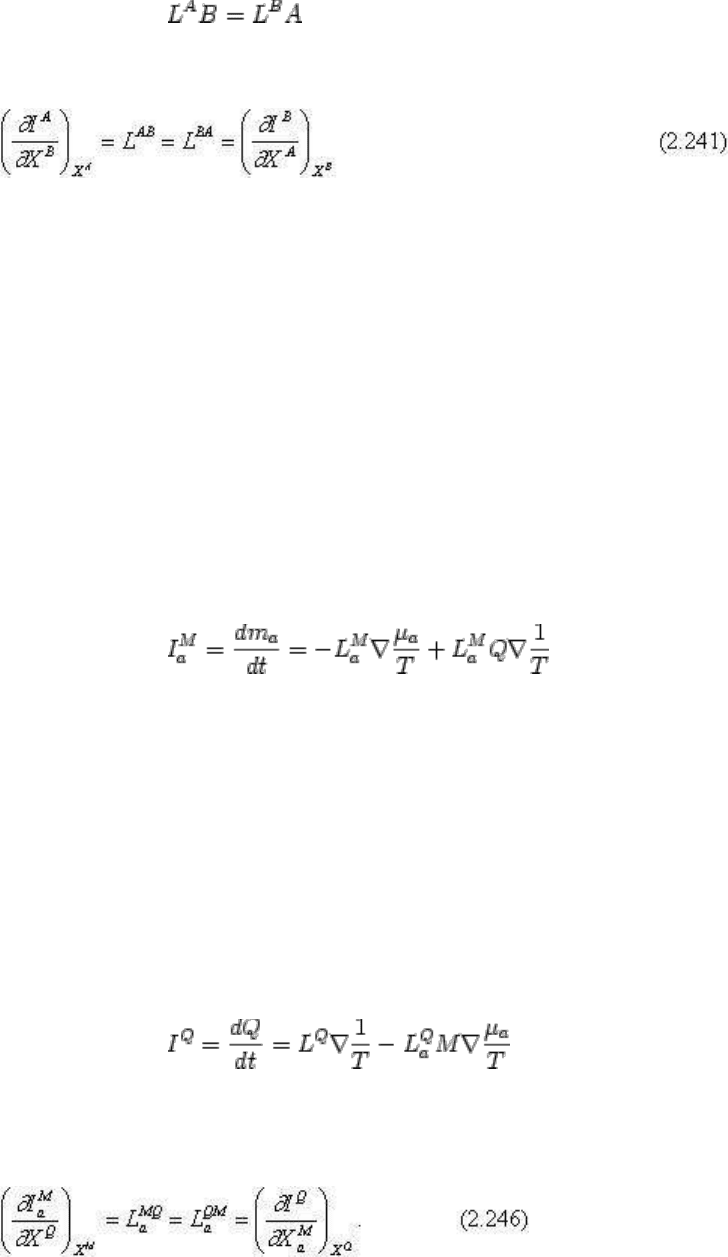
Принцип взаимности Онзагера устанавливает соотношение между различными
процессами, протекающими в системе одновременно. Он записывается как:
.
(2.240)
или
и формулируется: <при соответствующем выборе потоков и сил матрица кинетических
коэффициентов симметрична>. Иначе говоря, обнаруживается сходное влияние
действующих сил на инородные потоки, если, естественно, эти силы и потоки записаны в
соответствии с уравнением скорости возрастания энтропии. Лучше всего
проиллюстрировать принцип взаимности на примере. Рассмотрим систему с градиентами
температуры и химического потенциала, например, компонента a. Перенос вещества в
такой системе будет происходить вследствие градиента химического потенциала
(собственно диффузия, или хемодиффузия) и вследствие градиента температуры
(термодиффузия). Уравнение потока компонента a запишется в общем виде как:
I
a
M
= L
a
M
X
a
M
+ L
a
MQ
X
a
Q
.
(2.242)
или, расшифровывая действующие силы:
.
(2.243)
Перенос тепла также будет происходить как вследствие градиента температуры, так и
вследствие градиента химического потенциала (это явление, обратное термодиффузии,
известно как эффект Дюфора).
Уравнение потока тепла выразится в общем виде как:
I
a
Q
= L
a
Q
X
a
Q
+ L
a
QM
X
a
M
.
(2.244)
и, расшифровывая действующие силы:
.
(2.245)
Используя соотношение взаимности (2.241), можно записать следующее уравнение:
откуда наглядно видно
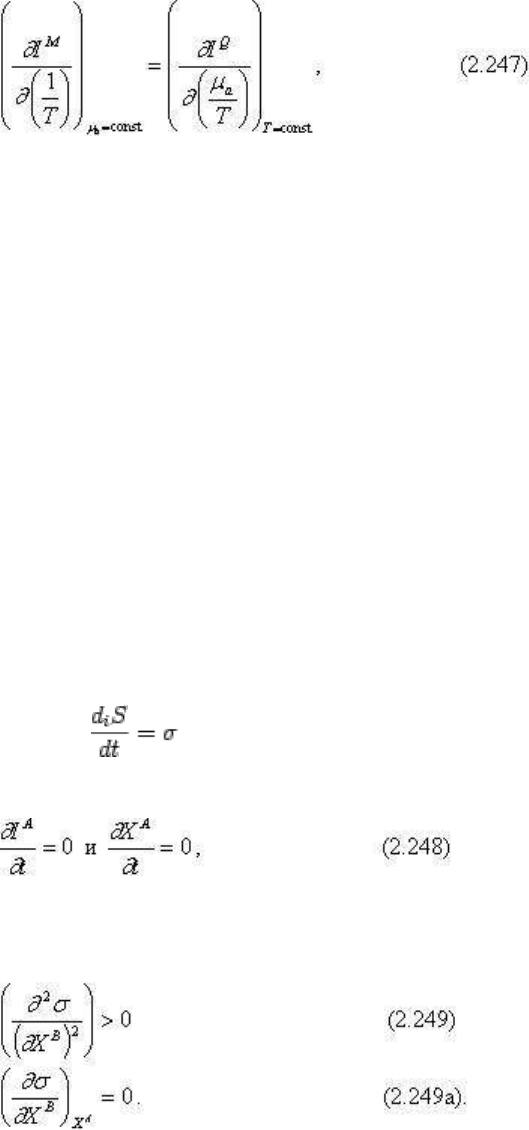
что изменение потока вещества, вызванного наложением тепловой силы (градиента
температуры), равнозначно изменению потока тепла вследствие наложения градиента
химического потенциала компонента. Отнесенные к единице наложенной силы потоки
вещества и тепла равны.
Отметим еще раз, что принципы Онзагера - фундаментальные обобщения необратимой
термодинамики - справедливы только при соответствующем выборе потоков и сил,
который определяется основным уравнением необратимой термодинамики - уравнением
производства энтропии.
Стационарные состояния
Особенно эффективно термодинамика необратимых процессов изучает стационарные
состояния, т. е. такие, отличные от равновесных состояния, которые не изменяются во
времени.
Стационарные состояния, как было впервые показано И. Пригожиным, характеризуются
минимальной скоростью возрастания энтропии. Тогда, обозначив для краткости, как это и
принято , условие минимальной скорости возрастания энтропии запишется так: ζ
= min при I
A
X
A
= const, где
а это означает, что
Покажем это простейшим способом. Действительно, если в системе имеется какой-либо
стационарный поток и I
A
X
A
= const, то минимум энтропии будет выполняться, если
другие, сопряженные или вынужденные потоки будут равны нулю. Пусть в схеме
возможен вынужденный поток I
B
, тогда:
ζ = I
A
X
A
const
+ I
B
X
B
.
и
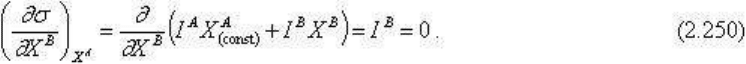
Существуют и более развернутые доказательства тождественности условий минимума
скорости возрастания энтропии и равенства нулю всех остальных вынужденных потоков.
Физический смысл этих условий легко пояснить следующим образом. Представим
систему в состоянии, когда в ней существуют градиенты интенсивных параметров,
например температуры и химических потенциалов каких-либо компонентов. В такой
системе должны, очевидно, протекать процессы выравнивания интенсивных параметров,
выражаемые потоками тепла и вещества, вплоть до достижения состояния равновесия.
Для осуществления стационарного состояния необходимо, чтобы какими-то внешними
условиями существования системы градиенты каких-либо параметров, например
температуры, были закреплены и поддерживались неизменными во времени ∂X
Q
/∂t = 0. В
таком случае к какому-то моменту в системе протекут все другие естественные процессы,
кроме единственного, поддерживаемого наложенным градиентом интенсивного
параметра. В нашем примере прекратится перенос вещества, и через систему будет
проходить только постоянный стационарный поток тепла, вызванный наложенным на
систему градиентом температуры. Мерой отклонения систем от состояния равновесия
служит ее энтропия. Энтропия будет возрастать по мере протекания естественных
процессов, вплоть до состояния минимальной скорости роста, которое осуществится в
стационарных условиях, поскольку все другие процессы, вызывающие возрастание
энтропии, будут уже исчерпаны. Как уже отмечалось, из этого вытекает важнейшее
свойство стационарных состояний - вынужденные потоки, сопряженные с действием
изменяющихся сил, в стационарных системах равны нулю.
В нашем примере это означает, что в системе с наложенным постоянным температурным
градиентом потоки вещества, сопряженные с изменяющимися силами ∇(μ/T), равны нулю.
Стационарное состояние, при котором внешними условиями удерживается постоянным
(не зависящим от времени) градиент какой-либо одной действующей силы, именуется
стационарным состоянием первого порядка. В случае постоянных градиентов каких-либо
двух действующих сил осуществляется стационарное состояние второго порядка и т. д.
Отметим, что стационарные состояния высших порядков - свыше первого - вполне
обычны для природных процессов. В таком случае, соотношение, когда d
i
S/dt = ζ = 0 и S =
const, можно именовать стационарным состоянием нулевого порядка, которое не что иное
как полностью равновесная система с k+2 независимыми параметрами и максимумом
энтропии или минимумом термодинамического потенциала системы.
Некоторые приложения термодинамики необратимых процессов
Для иллюстрации приложения методов необратимой термодинамики к природным
процессам рассмотрим несколько показательных примеров.
Явления термодиффузии и бародиффузии. Пусть на систему наложен градиент
температуры. В соответствии с характером действующих сил градиент температуры будет
вызывать изменение химических потенциалов компонентов и диффузию вещества. В свою
очередь термодиффузия будет приводить к изменению концентрации компонентов и
вследствие этого вызывать противодействующую ей концентрационную диффузию, или
хемодиффузию компонентов, стремящуюся ликвидировать градиент концентрации,
вызванной термодиффузией. Для какого-либо компонента а общий поток выразится как
