Жариков В.А. Основы физической геохимии

Подождите немного. Документ загружается.

Парциальные величины характеризуются следующими важными свойствами (приводятся

без подробного доказательства, интересующиеся могут ознакомится с полным курсом

химической термодинамики).

1. Первое очевидное свойство:

(2.87)

Разделив уравнение на , получим

2. Дифференцируя при постоянных q

,... q

, получим

(2.89)

3. Дифференцируя (2.87) одновременно по q и m, а уравнение (2.88) по q и х и сравнивая

полученные уравнения соответственно с (2.89) и (2.90), приходим к следующим

зависимостям:

(2.91)

(2.92)

Обратим внимание на то, что во всех уравнениях, где массы заменены мольными долями,

парциальная величина остается в соответствии с определением (2.84) частной

производной по массе.

Для того чтобы нагляднее представить существо приведенных уравнений и вывести

некоторые другие полезные соотношения обратимся для простоты к двухкомпонентной

системе.

Прежде всего напомним, что состав бинарной системы может быть задан массами двух

компонентов: mа и mb или мольной (или весовой) долей одного из них: x

или x

, т.е. в

соответствии с (2.81), x

=1, x

=1-x

и, дифференцируя,

(2.93)

Из уравнений (2.87)-(2.92) вытекают следующие важные соотношения между

парциальными величинами в бинарной системе:

откуда дифференцируя по xb выведем важную формулу:

Подставляя (2.95) в (2.94) получим известное уравнение:

которое показывает изменение в зависимости от состава бинарной системы.

Уравнения (2.91) и (2.92) могут быть выражены через частные производные, давая при

этом серию употребляемых в химической термодинамике соотношений (cм.подробнее

Акопян, 1963, Кричевский, 1962 и др.). Например:

или, выраженные в мольных долях

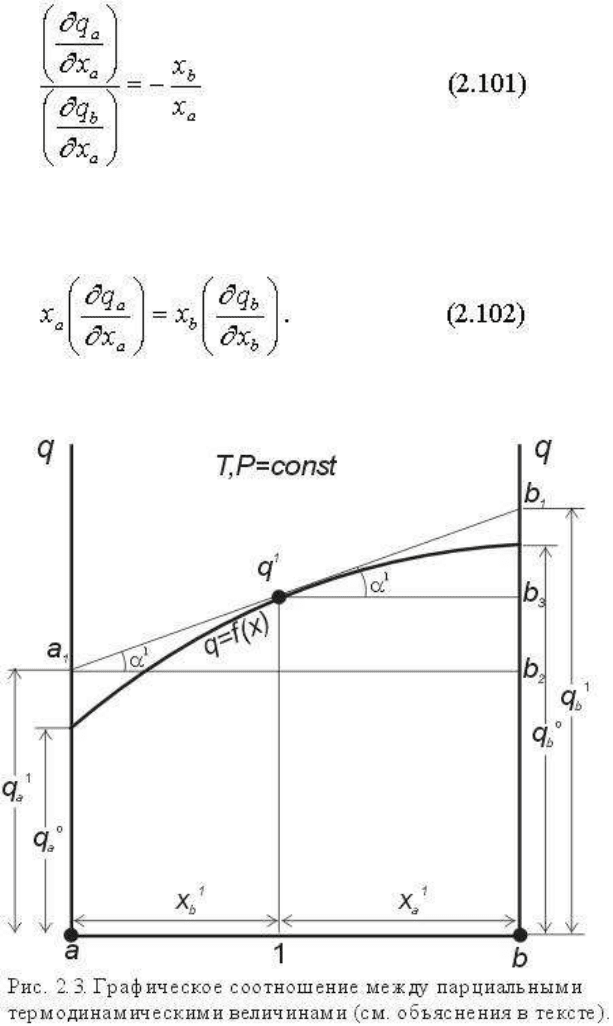
и, преобразуя (2.99), получим:

или с учетом (2.93)

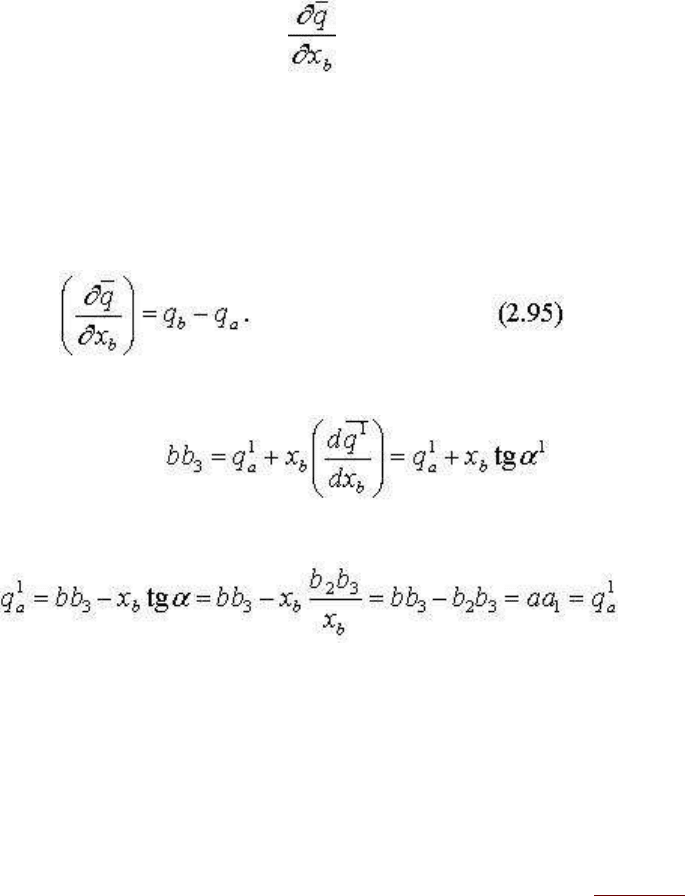
Рассмотренные соотношения имеют наглядное графическое изображение.

На рис. 2.3 представлена диаграмма, где по оси ординат отложена любая экстенсивная

характеристика q, а по оси абсцисс - мольные доли компонентов. На диаграмме нанесена

кривая q=f(x) при условии Т,р= const, на которой произвольно выбрана точка 1 и в ней

проведена касательная к кривой. Ордината этой точки q

, а продолжение касательной до

пересечения с осями q в точках x

= 1 (x

= 0), x

= 1 (x

= 0) и отсекает на них отрезки a

= q

и b

b = q

. Это очевидно из выражения (2.67) в простейшем случае, когда q

, q

не

зависят от состава, при x

= 1 получим q = q

, а при x

= 1 соответственно q = q

, и

функция q=f(x) будет представлена прямой, соединяющей q

и q

. В общем случае, когда

и q

изменяются в зависимости от х, принятое утверждение следует доказать. Проще

всего это сделать следующим образом. Производная

в точке 1 равна dq

/ dx

= tg α

(см. рис. 2.3). Но отрезок a

=ab=1, поскольку x

=1.

Тогда tg α

= b

/ 1 = bb

- bb

= bb

- aa

= q

- q

и окончательно dq

/ dx

= q

- q

. Это

справедливо для каждой точки кривой q=f(x), кроме, естественно, x

= 0. Таким образом,

графически доказывается выведенное раньше уравнение (2.95):

Уравнение (2.96) графически на рис. 2.3 выражается следующими соотношениями

отрезков .

Решая его относительно q

получим

Аналогично можно показать, что bb

. Тем самым дoказывается, что касательная к

кривой q=f(x) отсекает по ординате при x

=0 и x

=0 соответственно парциальные

величины q

и q

. Вспомним в связи с этим уже сделанное замечание о том, что только

производная по массе от экстенсивного параметра представляет парциальную величину.

Нетрудно видеть из выражения (2.95), что физический смысл производной по мольной

доле уже иной.

Уравнения (2.70) и (2.71), их графическая интерпретация (см. рис. 2.1) имеют

существенное значение для вычисления парциальных характеристик по мольным и

обратно. Из приведенных выше уравнений (2.99-2.102) следует ряд важных свойств

парциальных величин, но эти свойства достаточно очевидны, например, изменение

парциальной величины одного компонента вызывает изменение ее и для другого

компонента. Поэтому уместно их рассматривать непосредственно в приложении к

конкретным задачам.

Парциальные величины в системах с вполне подвижными компонентами следует

определить как приращение любого экстенсивного параметра при бесконечно малом

изменении массы какого-либо компонента при постоянных температуре, давлении,

химических потенциалах и массах всех других компонентов. Покажем, что парциальная

величина представляет индивидуальную характеристику каждого компонента независимо

от того являются в системе независимыми интенсивными параметрами только

температура и давление или в их число входят химические потенциалы вполне

подвижных компонентов.

Рассмотрим двухкомпонентную изотермо-изобарическую систему. Ее термодинамический

потенциал G = ƒ(p, T, m

, m

) в интегральной форме равен

(2.103)

Производные от G по m

и от G по m

соответственно равны парциальным свободным

энергиям или химическим потенциалам компонентов a и b:

Обратимся теперь к системе, где кроме инертных компонентов a и b присутствует вполне

подвижный компонент j , фактором состояния которого является интенсивный параметр -

его химический потенциал.

Термодинамический потенциал системы G

= ƒ(p, T, m

, m

, μ

) в интегральной форме

равен

(2.105)

Взяв производную от G

по m

и от G

по m

, получим соответственно их парциальные

свободные энергии - химические потенциалы:

которые никак не зависят от вполне подвижного компонента и идентичны рассмотренным

выше (2.103). Представим, что из значения свободной энергии трехкомпонентной системы

(a, b, j) удалена энергия приходящаяся на вполне подвижный компонент, и парциальные

свободные энергии компонентов a и b остаются такими же, как и в ранее рассмотренной

системе (ab).

Определим теперь значения других парциальных величин - энтропии и объема - в

системах с вполне подвижными компонентами на примере той же системы G

= ƒ(p, T,

, m

, μ

Возьмем производную по температуре от разных частей уравнения (2.105:

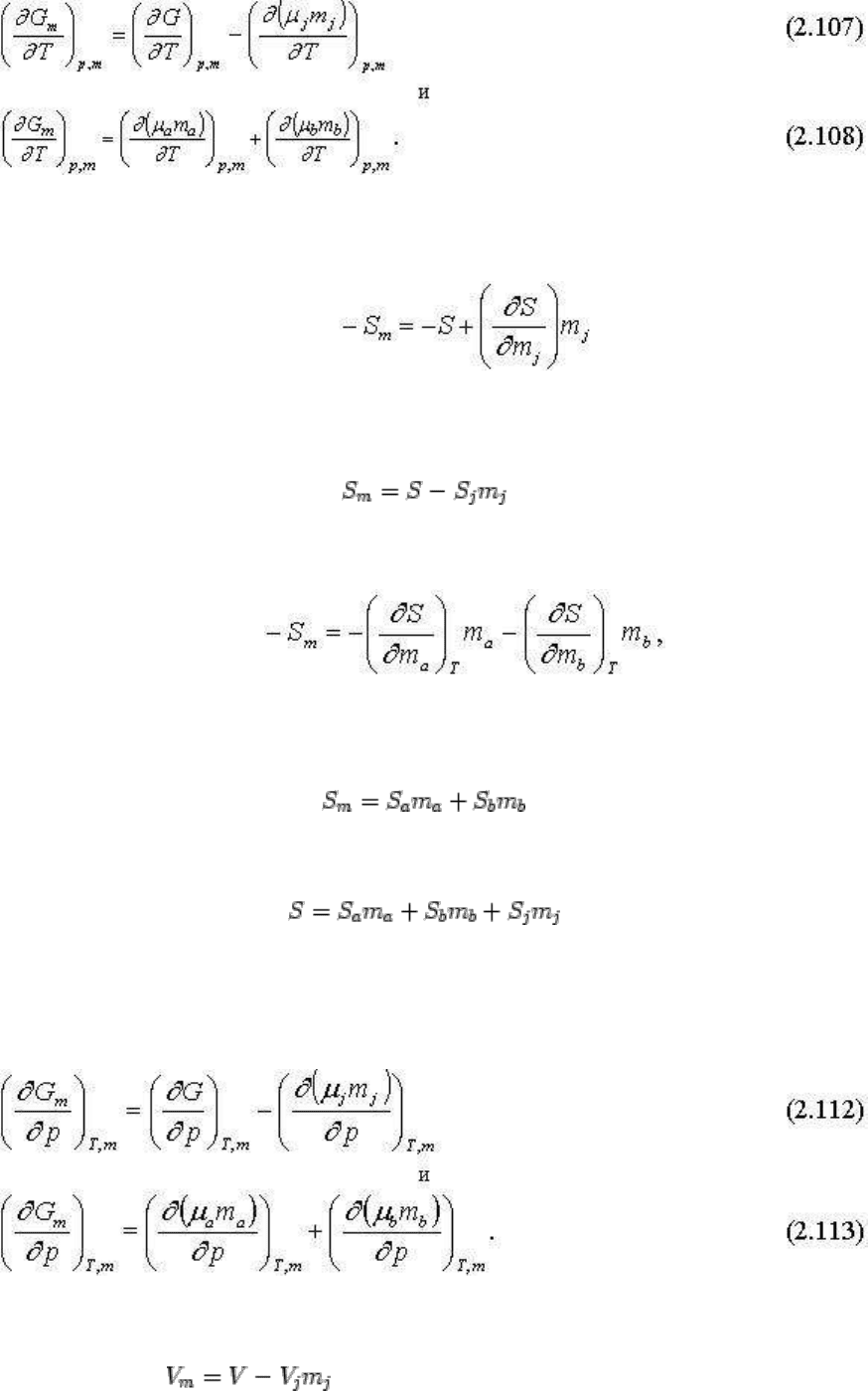
Используя приведенные выше соотношения (2.69) и (2.74), получим:

или

(2.109)

а также

или

(2.110)

и, наконец,

(2.111)

Аналогичным путем для парциальных объемов мы получим необходимые соотношения,

взяв от разных частей уравнения (2.105) производные по давлению

Откуда, используя выведенные ранее уравнения (2.66), (2.70), получим соотношения:

(2.114)

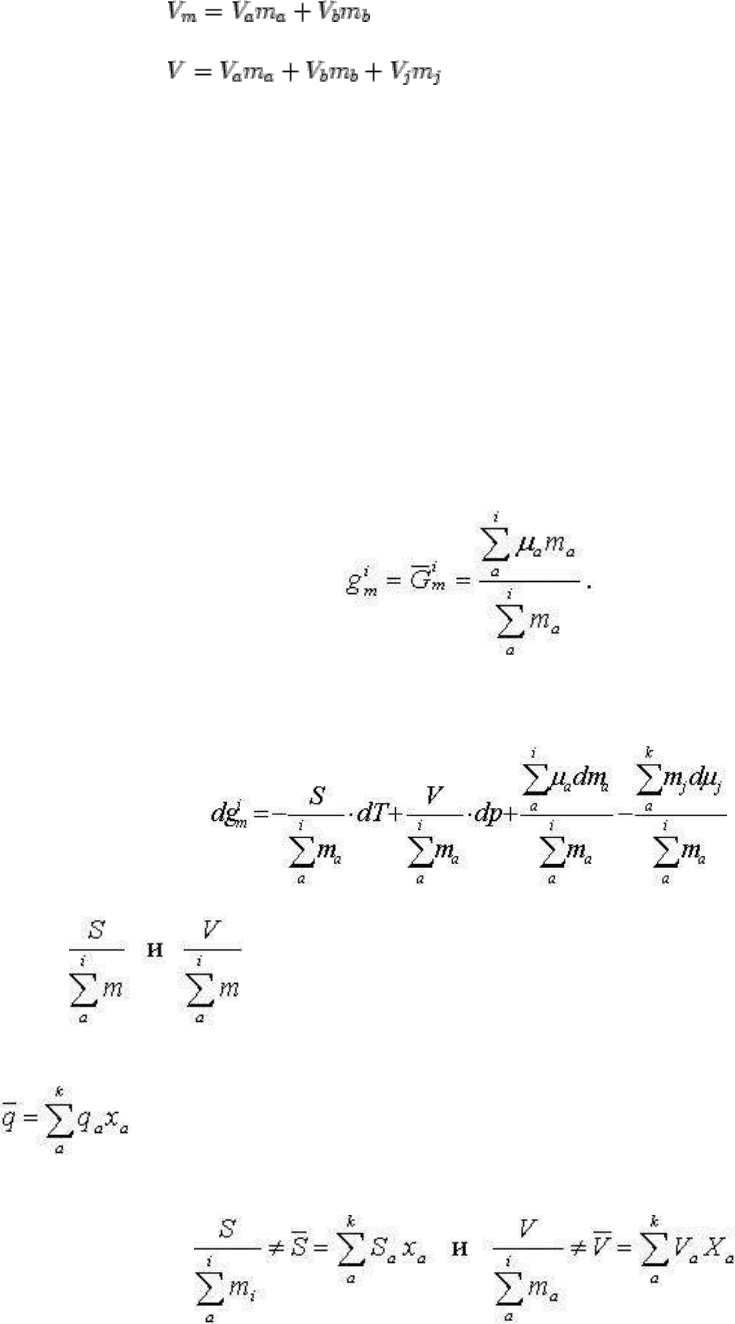
(2.115)

(2.116)

полностью симметричные выведенным выше для энтропии.

Таким образом парциальные энтропии и парциальные объемы представляют

индивидуальные характеристики компонентов во всех типах систем (в том числе и в

системах с в.п.к.) и не зависят от режима других компонентов. В системах с в.п.к. общая

энтропия и общий объем системы слагается как взвешенная (умноженная на массу) сумма

парциальных энтропий и парциальных объемов всех компонентов - и инертных и вполне

подвижных.

Существенным моментом в термодинамике систем с вполне подвижными компонентами

является переход к удельным (мольным) характеристикам. Из интегральной формы G

потенциала как бы следует, что мольная доля компонента должна определяться по

отношению к сумме масс инертных компонентов:

Но в таком случае оказывается, что в дифференциальном выражении g

-потенциала

члены

не будут представлять парциальные мольные энтропию и объем системы (которые равны

[2.88]), а энтропию и объем системы, отнесенные к массе инертных

компонентов, т. е.

Члены

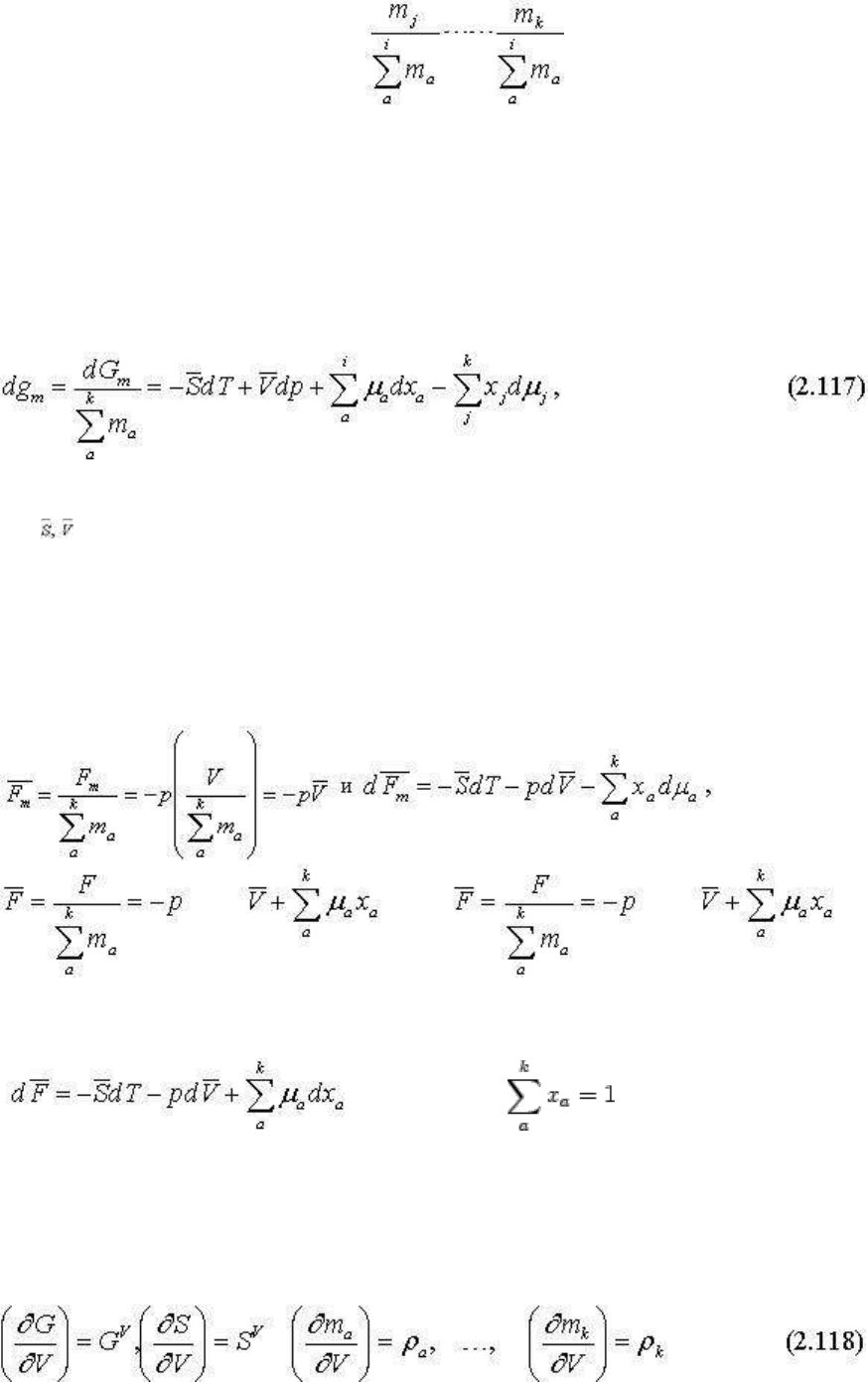
в этом уравнении выражают не мольные доли вполне подвижных компонентов в системе,

а их удельное количество приходящееся на сумму масс инертных компонентов.

Уравнение dg

оказывается термодинамически некорректным, поэтому нужно либо

правильно выразить термодинамический потенциал системы охватывающий только

инертные компоненты (Жариков 1987), что имеет определенный смысл в некоторых

частных приложениях, либо в общем случае отнести G

к сумме масс всех компонентов.

Тогда

где - мольные энтропия и объем системы, - мольные доли всех компонентов, причем

сумма их всегда равна единице, (сумма мольных долей инертных компонентов не равна

единице если в системе есть в.п.к.). Такой способ задания системы позволяет строго и

единообразно, относя к единице массы, описать все разнообразие систем с различным

термодинамическим режимом компонентов. Например, для изотермо-изохорической

системы с в.п.к. от состояния, когда все компоненты вполне подвижны:

до состояния где все компоненты инертны:

, причем всегда .

Таким образом, удельные характеристики, симметричные парциальным величинам,

можно получить взяв производную от экстенсивных параметров системы по другим

экстенсивным параметрам кроме масс компонентов. Ясный физический смысл, например,

имеют производные по объему:

где G

- объемная энергия (энергия единицы объема), S

- объемная энтропия (энтропия

единицы объема), ρ

...ρ

- мольные плотности компонентов (их количества в единице

объема). Если, наконец, разбить общий объем системы на сумму объемов V = V

+ V

+ ...

+ V

(например объемов фаз), то частные производные типа

вплоть до

обладают обычными свойствами парциальных величин:

а также

(см. уравнения 2.87, 2.89).

Химический потенциал

Из уравнения изотермо-изобарического потенциала (2.32)

на основании свойства полного дифференциала следует

Уравнения (2.119) показывают, что химический потенциал компонента представляет

парциальную свободную энергию компонента и соответственно характеризуется всеми

свойствами парциальных величин. Это наглядно видно (сравним с (2.87) и (2.88)) из

интегрального выражения изотермо-изобарического потенциала:

(2.120)

или для мольного потенциала:

Дифференцируя уравнение (2.121) при постоянных μ

...μ

, получим, например,

Уравнение (2.122) представляет изменение изотермо-изобарического потенциала при

постоянных Т и р, в системе без в.п.к., что очевидно из сопоставления (2.122) с (2.87).

Из выражения (2.121) видно:

при x

= 1,

т. е. мольный изотермо-изобарический потенциал однокомпонентной системы равен

химическому потенциалу компонента. Обратим внимание на следующие соотношения. Из

уравнений термодинамических потенциалов различных систем следует

Существо этих равенств наглядно проступает в сравнении с уравнением (2.86)

и, дифференцируя,

(2.120)

только в изотермо-изобарических условиях химический потенциал компонента равен

изменению парциальной свободной энергии - термодинамического потенциала системы.

Парциальные термодинамические потенциалы других систем в изотермо-изобарических

условиях должны быть "исправлены" на другие виды работ, если мы хотим выделить

парциальную химическую энергию из общего парциального термодинамического

потенциала системы. В то же время производные по массе от термодинамических

потенциалов при постоянстве факторов состояния систем (уравнение 2.121) всегда равны

химическим потенциалам компонентов.

Для бинарной системы из уравнений (2.94) - (2.100) непосредственно следуют важные

зависимости:

(2.125)

(2.126)

∂g / ∂x

= μ

- μ

(2.127)