Жариков В.А. Основы физической геохимии
Подождите немного. Документ загружается.

n
T, μ
= k
i
+ k
m
+ 2 - r -ƒ
in
= k
i
+ 1 - r, r
T, μ
max
= k
i
+ 1
(2.56)
n
p, μ
= k
i
+ k
m
+ 2 - r -ƒ
in
= k
i
+ 1 - r, r
p, μ
max
= k
i
+ 1
(2.57)
Полученные соотношения приводят к следующим важнейшим выводам.
1. Число фаз в системах с вполне подвижными компонентами не зависит от числа вполне
подвижных компонентов и определяется экстенсивными параметрами систем, в число
которых входят массы инертных компонентов, а также (в соответствующих системах)
объем и энтропия.
2. Химические потенциалы вполне подвижных компонентов, являясь интенсивными
факторами состояния, играют такую же роль, как температура и давление, определяя
разнообразие фазового (минерального) состава и фазовых равновесий (парагенезисов), и
условия их существования в системах с вполне подвижными компонентами.
Рассмотренные положения имеют фундаментальное значение для физико-химического
анализа природных систем. Они показывают принципиальную особенность природных
систем, состоящую в том, что число минералов в природных системах всегда меньше
числа слагающих их компонентов и, напротив, разнообразие минерального состава и
парагенезисов значительно шире, поскольку оно зависит не только от температуры и
давления, но и от величин химических потенциалов (или других интенсивных параметров)
вполне подвижных компонентов.
В свете изложенного становятся ясными неудачи первоначального применения правила
фаз к анализу парагенезисов: минералогическое правило фаз Гольдшмидта (r=k) не
учитывало главной особенности природных систем - вполне подвижного поведения ряда
компонентов, не влияющего на число фаз. Только открытие систем с вполне подвижными
компонентами и, как следствие, новая форма правила фаз создали необходимую
теоретическую основу физико-химического анализа парагенезисов. Соотношения (2.55) -
(2.57), впервые выведенные Д. С. Коржинским, со временем получили наименование
<правила фаз Коржинского>.
Термодинамические потенциалы систем с ионизированными вполне подвижными
компонентами
Многие природные процессы минералообразования протекают в присутствии водных
растворов и поэтому компоненты, в них участвующие, оказываются в той или иной
степени ионизированными. Нередки также в природных условиях окислительно-
восстановительные процессы, которые совершаются одновременно с изменением
кислотности растворов или независимо от нее.
При рассмотрении равновесий с ионизированными компонентами существенным является
вопрос о правильном выборе независимых компонентов, поскольку в системах
происходит взаимодействие компонентов с раствором с образованием за счет
растворителя одинаковых частиц (группы Н
+
и ОН
-
) и на системы в общем случае
наложено условие электронейтральности.
В тех случаях, когда в растворе кроме Н
2
О присутствует какой-либо один компонент
(например, Na
2
O), общее содержание или концентрация компонента и концентрация его
ионных форм связаны константами диссоциации. Например,
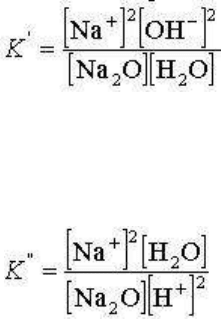
Na
2
O + Н
2
О = 2NaOH = 2Na
+
+ 2OH
-
и константа реакции
Учитывая Н
2
О = Н
+
+ ОН
-
, эту реакцию можно записать и так: Na
2
O + 2Н
+
= 2Na
+
+ Н
2
О с
константой
.
В приведенных выражениях в квадратных скобках обозначены концентрации или в общем
случае активности соответствующих компонентов. Поскольку К' и К" различаются
величиной константы диссоциации воды и эта величина постоянная при данных T и p, то
в качестве независимой равноценно может быть принята любая из форм нахождения
компонента.
Сложнее обстоит дело с многокомпонентными растворами. В этом случае растворение
каждого из компонентов будет влиять на концентрацию ионов водорода и гидроксила, а
изменение кислотности раствора, в свою очередь, будет вызывать (в соответствии с
константами диссоциации) изменение концентрации ионных форм. Таким образом, общий
эффект взаимодействия компонентов в растворе выразится в каком-то определенном
суммарном уровне кислотности раствора и определенной общей или валовой
концентрации компонента, тогда как концентрация каждой конкретной ионизированной
формы будет, очевидно, находиться в зависимости от валовой концентрации компонента
и кислотности раствора. Соответственно в качестве независимых параметров
многокомпонентного раствора выступают суммарные валовые активности (концентрации)
или химические потенциалы компонентов и активность, или, точнее, химический
потенциал ионов водорода. Заметим при этом, что выбор химического потенциала иона
водорода в качестве независимой переменной представляет не только рациональный
термодинамический прием, но отражает условия существования природных систем,
режим кислотности в которых поддерживается главным образом индифферентными (т. е.
не участвующими в процессах минералообразования) вполне подвижными компонентами.
Вместе с тем следует указать, что при анализе парагенезисов часто вызывает интерес
зависимость минеральных равновесий от величины химического потенциала конкретного
иона, участвующего в реакции (особенно когда физико-химические данные позволяют это
рассчитать). Такая зависимость с успехом может быть исследована, однако следует
помнить, что активность иона зависит от кислотности раствора или - альтернативная
позиция, - если химический потенциал иона принять независимым, от кислотности
раствора будут зависеть общая концентрация и химический потенциал компонента (что,
конечно, искусственно).
Для обобщенной характеристики процессов окисления-восстановления в качестве
параметров сходным образом целесообразно принять не характеристики каких-либо
конкретных окисленных или восстановленных форм компонентов, а изменение общего
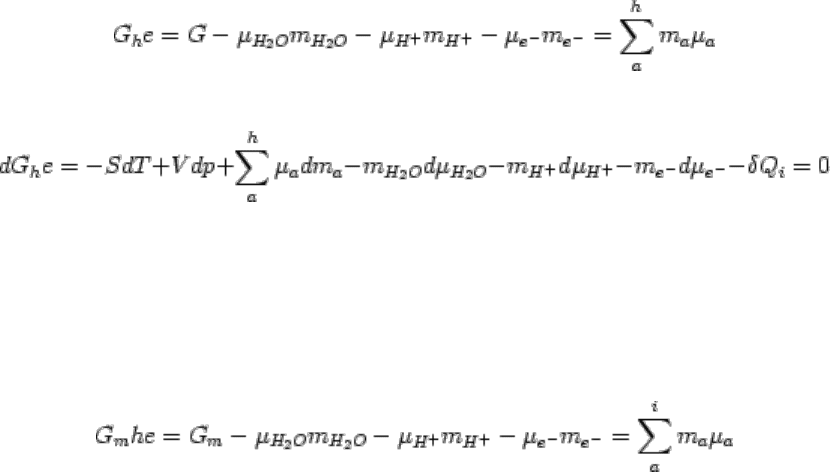
содержания электронов и окислительно-восстановительного потенциала (химического
потенциала электрона) системы. Обратим внимание, что, затрагивая процессы окисления-
восстановления, мы переходим к более сложным, нежели простые, термодинамическим
системам. В этих системах происходят электрические или электрохимические процессы,
которые также могут быть полностью охарактеризованы парой сопряженных параметров:
экстенсивным, который отражает количество электричества, содержащегося в системе, и
который в обобщенном виде можно обозначить как массу электронов m
e
-
, и интенсивным
параметром, который характеризует электрическую напряженность системы и который
мы аналогично тому, как это сделано для химической напряженности, обозначим как
химический потенциал электрона μ
e
-
. Соответственно элементарная электрохимическая
работа выразится как δZ
e
-
= μ
e
-δm
e
. Приведенные обозначения отличаются от
общепринятых в химической термодинамике, однако они имеют преимущество своей
обобщенностью и симметричностью. Нетрудно показать, и это будет сделано в
дальнейшем, что масса электронов может быть привычно выражена через произведение
числа зарядов на единичный заряд или число Фарадея, а химический потенциал электрона
представляет суть восстановительный потенциал.
Обобщенный способ выражения реакции в растворах с изменением кислотности и степени
окисления известен так же, как способ Пурбо, названный так по имени исследователя,
который подчеркнул, что любая химическая (или минеральная) реакция в присутствии
раствора может быть выражена в виде
аА + bВ + сС + dD +lН
2
О + mН
+
+ ne
-
= 0.
(2.58)
В общем случае, который имеет преимущественное значение для анализа парагенезисов,
кислотно-основные и окислительно-восстановительные равновесия протекают таким
образом, что кислотность и степень окисления не зависят от реакций внутри системы a,
определяются внешними условиями существования системы и факторами состояния
являются химические потенциалы протона (иона водорода), электрона и, в силу уравнения
(2.58), химический потенциал воды. Такие системы можно обозначать как системы с
внешне контролируемой кислотностью и степенью окисления или системы с вполне
подвижными протоном и электроном. Термодинамический потенциал изотермо-
изобарической системы с вполне подвижными протоном, электроном и водой имеет вид
,
(2.59)
.
(2.60)
Наконец, в общем виде, когда кроме Н
2
О, Н
+
и e
-
в системе присутствуют другие вполне
подвижные компоненты, термодинамический потенциал - свободная энергия Гиббса такой
системы равен:
(2.61)
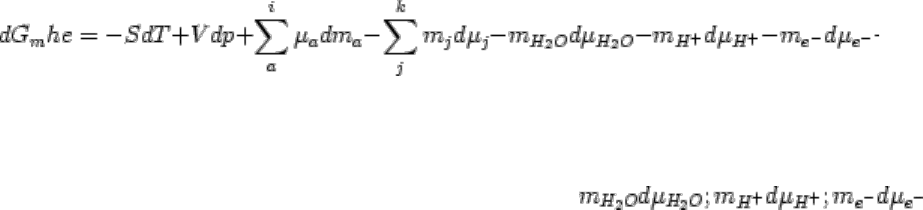
,
.
(2.62
)
Очевидно, что функции U
mhe
, H
mhe
, F
mhe
будут иметь подобный вид, отличаясь от U
m
, H
m
и
F
m
, так же как G
mhe
от G
m
, выделенными членами: и
представляют, по существу, разновидности термодинамических потенциалов систем с
вполне подвижными компонентами. Поэтому нет надобности повторять их
характеристики, они обладают всеми свойствами термодинамических потенциалов. Далее,
в соответствующих разделах мы покажем как элементарными условиями стандартизации
(кстати необходимым и для всех μ
В.П.К.
) выражение μ
H+
и μ
e-
приводится к привычным pH
и Eh.
В заключение раздела уместно снова вспомнить о методе теоретического моделирования,
поскольку открытие систем с вполне подвижными компонентами как термодинамической
модели природных систем - блестящий пример применения метода теоретического
моделирования в физической геохимии. Установление эмпирического принципа
дифференциальной подвижности компонентов - этап выявления исходных посылок. На
основании принципов и общих законов термодинамики выведены уравнения
термодинамических потенциалов нового типа систем с вполне подвижными
компонентами, представляющие теоретическую модель природных термодинамических
систем. Исследование модели привело к установлению новой формы правила фаз,
отражающей особенности формирования природных парагенезисов. Успешное
приложение правила фаз к анализу парагенезисов (этап проверки модели), не только
утвердило системы с вполне подвижными компонентами как термодинамическую модель
природных систем, но и открыло широкую дорогу физико-химическому анализу
парагенезисов минералов. Перейдем теперь к рассмотрению некоторых других
важнейших выводов из уравнений термодинамических потенциалов, а также
существенных для нашей цели термодинамических соотношений.
4. НЕКОТОРЫЕ ВАЖНЕЙШИЕ ТЕРМОДИНАМИЧЕСКИЕ СООТНОШЕНИЯ.
Термодинамические потенциалы как характеристические функции системы
Напомним, что термодинамические потенциалы служат характеристическими функциями
системы в том смысле, что производная от термодинамического потенциала по
термодинамическому параметру также является термодинамическим параметром.
Термодинамический потенциал представляет полный дифференциал как функция k+2
независимых параметров - факторов состояния системы. В системе с k+2 независимыми
параметрами все другие параметры могут быть выражены как функции этих k+2 факторов
состояния.
Отмеченные свойства широко используются в термодинамике для выведения
интересующих зависимостей в любых типах термодинамических систем. Рассмотрим
несколько соотношений, которые будут полезны нам в дальнейшем.
Энтальпия системы с вполне подвижным компонентом является полным дифференциалом
системы H = ƒ(S, p, m
a
,..., m
i
, μ
j
,...,μ
k
):
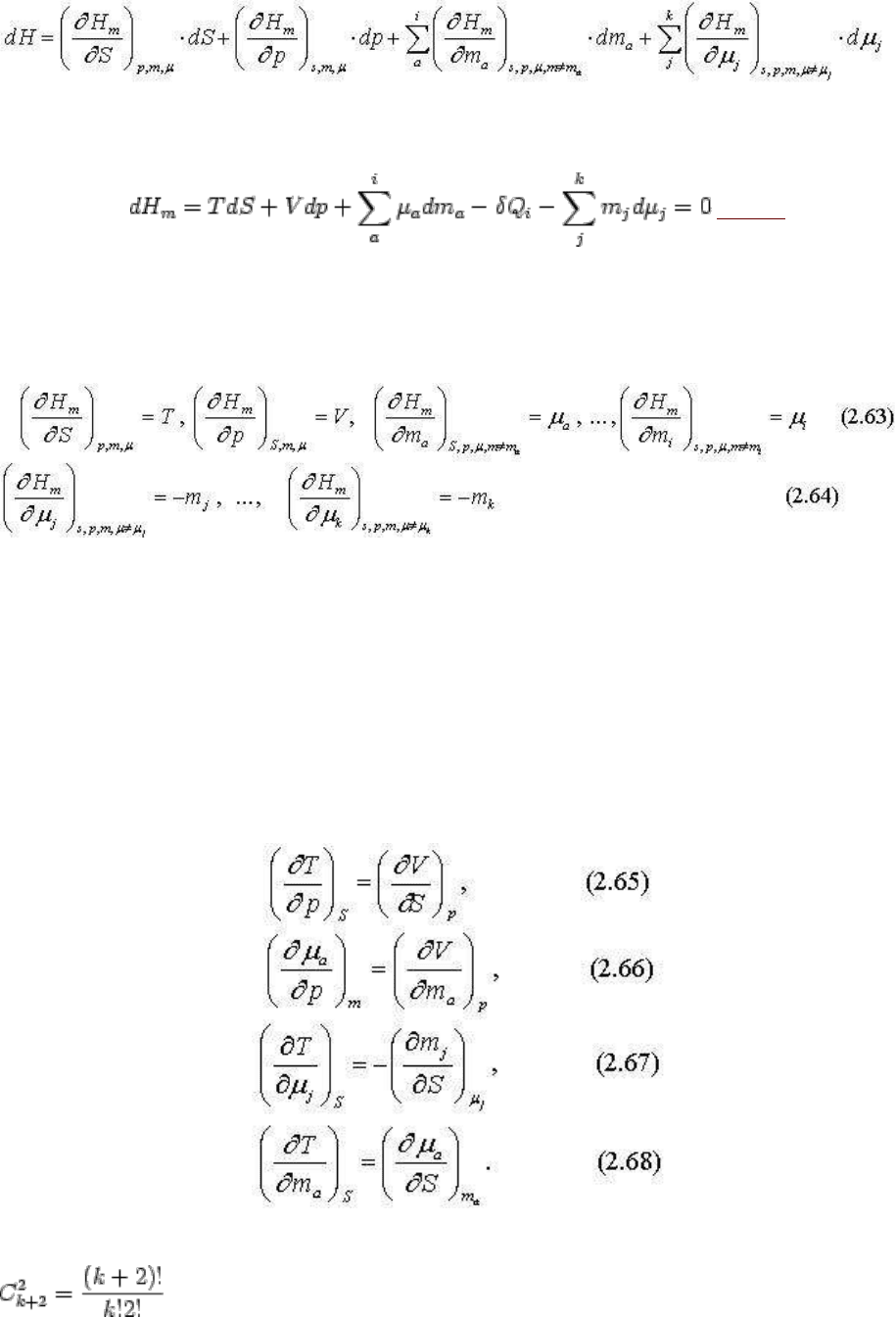
в тоже время
(2.47)5
откуда очевидна зависимость энтальпии от k+2 факторов состояния системы:
Увеличение энтропии, давления и масс компонентов приводит к росту энтальпии системы
пропорционально температуре, объему и химическим потенциалам компонентов, а
повышение химических потенциалов уменьшает энтальпию системы пропорционально
массам вполне подвижных компонентов, впрочем эти зависимости и так видны из
уравнения (2.47).
Значительно более интересные соотношения могут быть получены из уравнения (2.47) как
полного дифференциала путем перекрестного дифференцирования. Например:
Нетрудно убедиться, что для системы из k компонентов таких соотношений будет
. Некоторые из них, например (2.65), (2.66), (2.67), имеют ясный
физический смысл, показывая каково взаимное влияние интенсивных параметров в
зависимости от изменения сопряженных экстенсивных параметров. Например, уравнение
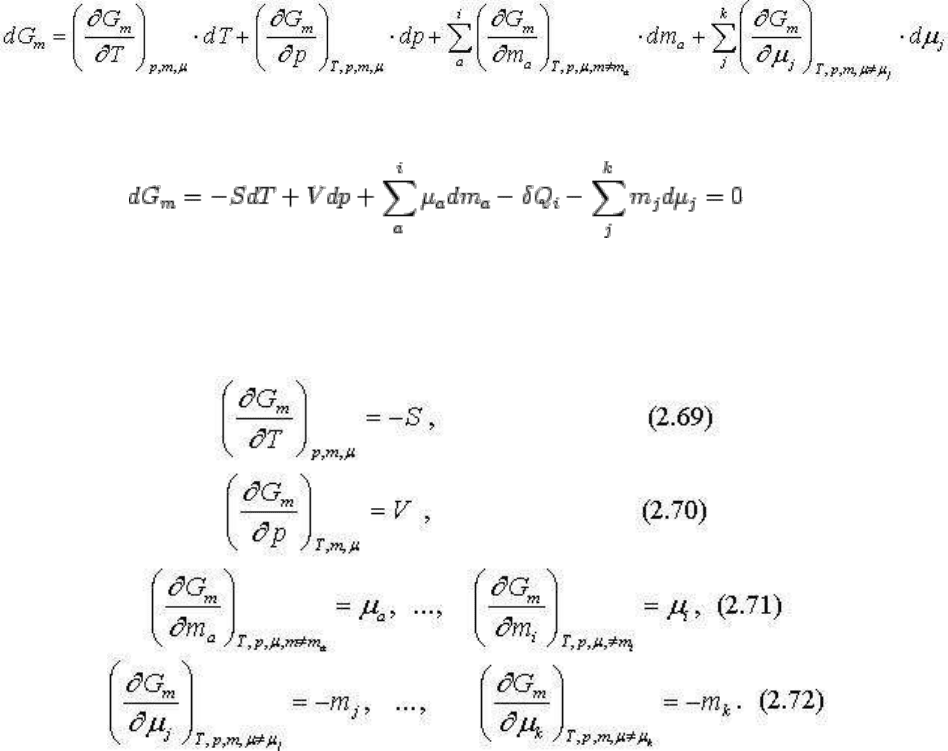
(2.64), как влияет на температуру давление в зависимости от изменения сопряженных
экстенсивных параметров - энтропии и объема. В других случаях (при производных
интенсивных параметров по экстенсивным и наоборот), как например, уравнение (2.68)
полученные соотношения не имеют реального значения или оно становится понятным
после соответствующих преобразований.
Рассмотрим в качестве второго примера изотермо-изобарическую систему с вполне
подвижными компонентами: G = ƒ(T, p, m
a
,..., m
i
, μ
j
,...,μ
k
). Ее полные дифференциалы:
и
.
(2.49)
тогда
Из этих уравнений очевидны зависимости G
m
-потенциала: при повышении температуры и
химических потенциалов вполне подвижных компонентов он уменьшается, при
увеличении объема и масс инертных компонентов - увеличивается.
Путем перекрестного дифференцирования выведем несколько полезных соотношений:
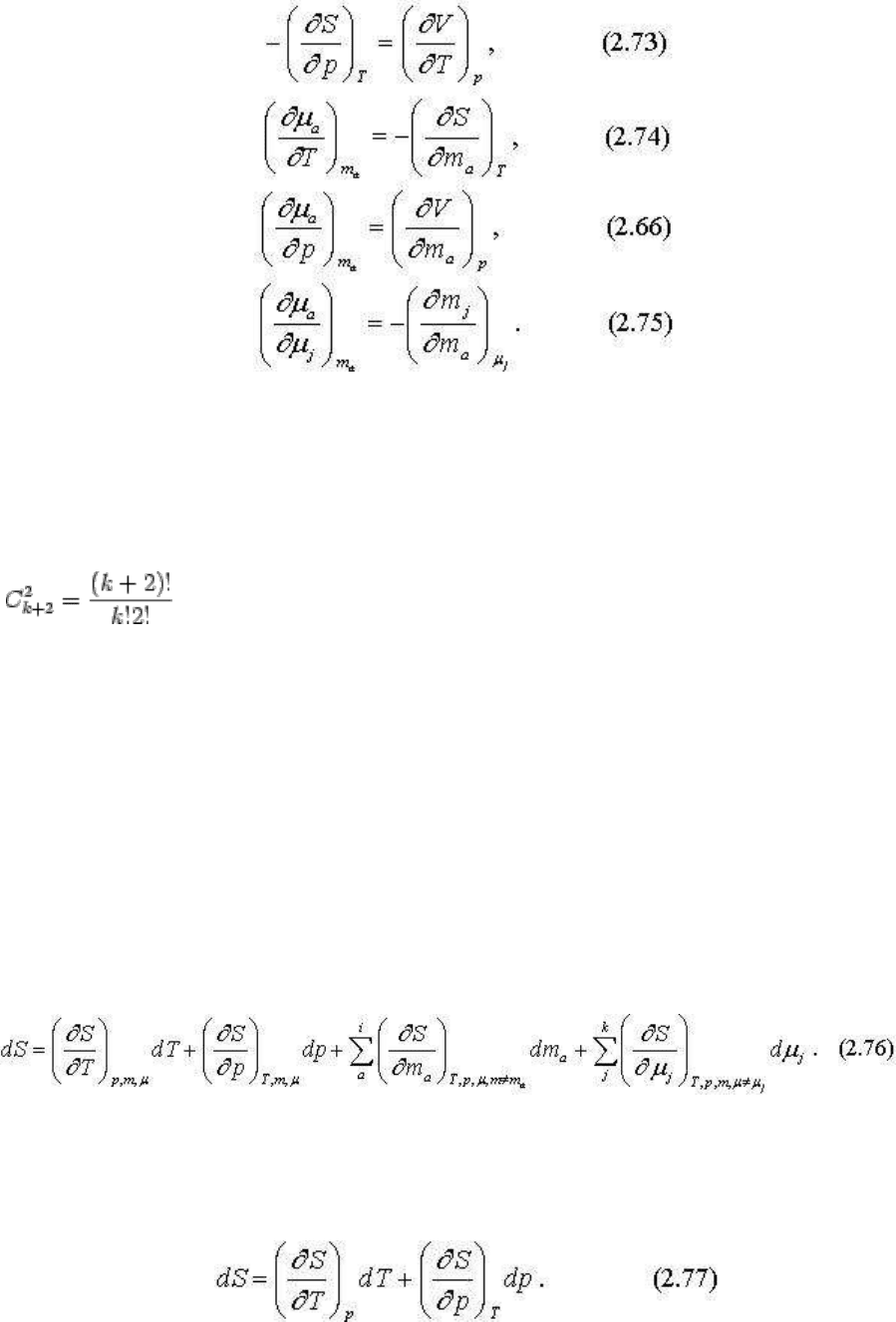
Уравнения (2.74-2.75) показывают явную зависимость химического потенциала инертного
компонента а от температуры (уменьшается), давления (увеличивается) и химического
потенциала вполне подвижных компонентов (уменьшается). Уравнение (2.73) не имеет
столь явный физический смысл - его мы раскроем немного позже. Как уже отмечалось, в
системе из k компонентов возможны
соотношения в виде частных производных, полученных перекрестным
дифференцированием по факторам состояния. Эти соотношения позволяют выявить
искомые взаимосвязи термодинамических параметров системы.
Другой прием, которым можно пользоваться для установления нужных зависимостей
между термодинамическими характеристиками, состоит в том, что если система задана
k+2 факторами состояния, которые являются независимыми параметрами, то любой
другой зависимый параметр может быть выражен в виде полного дифференциала от
факторов состояния системы. Так для системы G
m
= ƒ(T, p, m
a
,..., m
i
, μ
j
,...,μ
k
) можно
выразить S = ƒ(T, p, m
a
,..., m
i
, μ
j
,...,μ
k
), V = ƒ(T, p, m
a
,..., m
i
, μ
j
,...,μ
k
), μ
a
= ƒ(T, p, m
a
,..., m
i
,
μ
j
,...,μ
k
), m
j
= ƒ(T, p, m
a
,..., m
i
, μ
j
,...,μ
k
) и т. д. Покажем это на примере энтропии:
Примем химическое состояние системы постоянным, т. е. dm
a
= dm
b
= ... = dm
i
= 0, dμ
a
= ...
= dμ
i
= 0 - тогда уравнение (2.76) предстанет в виде
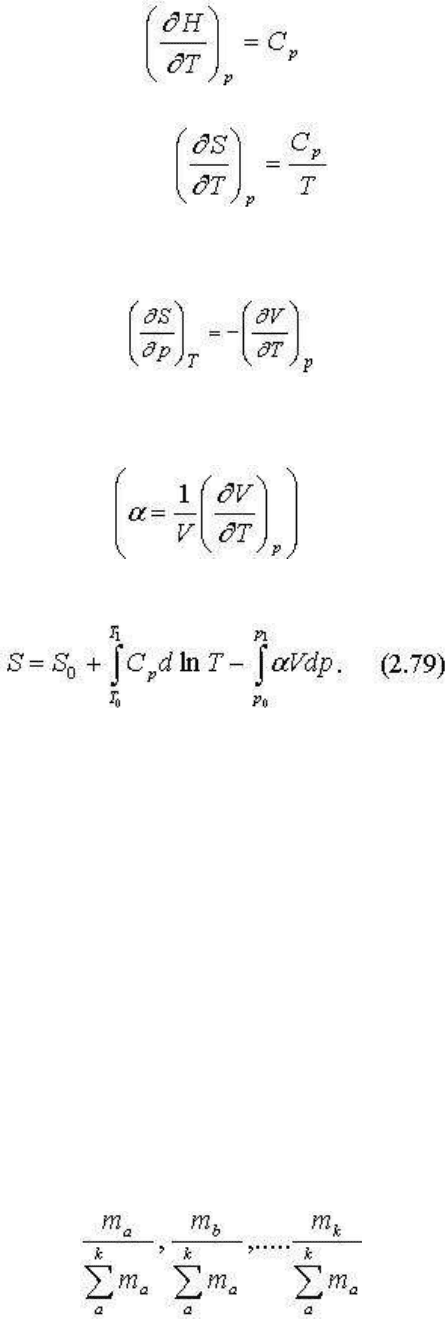
Раскроем значения частных производных переходя тем самым от канонических
термодинамических уравнений к обычным функциональным зависимостям. Как известно
,
тогда .
Другая производная согласно (2.73) равна
,
но если ввести термический коэффициент расширения α
, то
Отметим, что для получения различных неканонических зависимостей между
термодинамическими величинами в некоторых обстоятельных термодинамических курсах
и работах используется метод якобиан (метод определителей Якоби). Он позволяет
получить выражения нескольких функций от нескольких переменных. Однако заметная
громоздкость вычислений и, главное, необходимость раскрывать полученные выражения
через производные первичных термодинамических параметров и реальные
термодинамические зависимости, делают с нашей точки зрения, предпочтительным вывод
термодинамических соотношений непосредственно из уравнений термодинамических
потенциалов.
Парциальные (мольные и удельные) термодинамические характеристики
Состав многокомпонентной, системы должен быть задан (описан) массами слагающих
систему компонентов: ma, mb,..., mk, где масса может быть выражена или количеством
весовых единиц, или количеством молей (грамм-молекул) компонента. Для физико-
химического анализа систем оказывается значительно рациональней (в чем убедимся в
дальнейшем), когда массы компонентов выражены в относительных единицах
,

которые также могут быть весовыми или мольными долями. Тогда, если массы выражены
в мольных единицах (что более употребительно), т. е. представляют мольные доли
компонентов:
.
(2.80)
причем
.
(2.81)
Аналогичным образом в весовых единицах будем иметь:
.
причем
.
Обратим внимание, что мольные доли компонентов в фазах являются интенсивными
параметрами, а уравнение (2.81) имеет тот же смысл, что и уравнение Гиббса-Дюгема,
показывая, что по крайней мере один параметр для каждой фазы должен быть
экстенсивным6.
Если разделить все экстенсивные параметры, входящие в уравнение термодинамического
потенциала, на сумму масс компонентов, получим выражение удельного (если массы
были в весовых единицах) или мольного термодинамического потенциала:
В дифференциальной форме соответственно:
откуда видно, что переход к мольному потенциалу осуществляется делением всех
экстенсивных параметров системы на сумму масс компонентов системы, т. е. отнесением
их к единичной массе системы.
Окончательно имеем
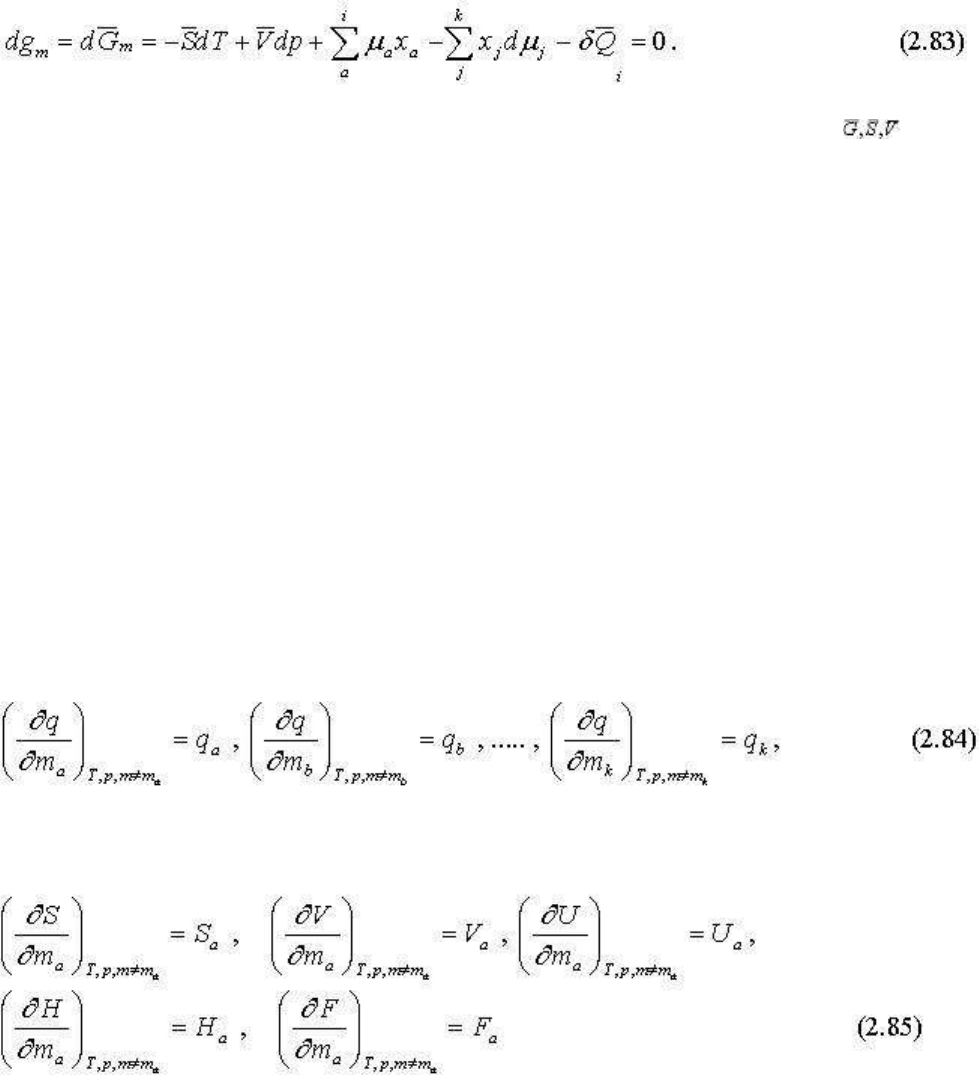
Мольные величины обычно записываются с черточкой над символам параметра и т.
д., мольный потенциал Гиббса обозначается нередко через g или δ, соответственно в
системах с в.п.к. g
m
, δ
m
, но в литературе чаще всего можно встретить запись мольного
потенциала в тех же символах, что и полного и только запись количеств компонентов в
виде мольных долей или масс однозначно обозначает мольный или полный потенциал.
Мы будем следовать этой традиции, вводя специальные символы потенциалов только в
тех случаях, когда это необходимо для правильного понимания.
Мольный потенциал чрезвычайно широко используется в термодинамике - как всякая
"удельная" характеристика он незаменим при сравнительном анализе.
Кроме мольного потенциала в химической термодинамике широко используются
удельные или мольные или, как их принято обозначать, парциальные характеристики
компонентов. Парциальными (мольными или удельными) называются экстенсивные
параметры, отнесенные к единице массы (количеству молей или весовых единиц) какого-
либо компонента. Парциальный параметр, или парциальная величина, равен приращению
соответствующего экстенсивного параметра при бесконечно малом изменении массы
какого-либо компонента, происходящем при постоянстве Т, р и масс других компонентов.
Согласно этому определению, если q - любой экстенсивный параметр, то
где q
a
, q
b
... q
k
- парциальные величины. Для простых термодинамических систем:
- парциальные энтропия, объем, энергии и энтальпии компонента а. Так же будут
выражены и парциальные характеристики всех других компонентов. Обратим внимание,
что только парциальная свободная энергия Гиббса равна химическому потенциалу
компонента, тогда как другие парциальные термодинамические потенциалы представляют
более сложные функции:
