Жариков В.А. Основы физической геохимии
Подождите немного. Документ загружается.


Как было впервые показано В. Гиббсом, сформулированному критерию равновесия
полностью эквивалентен другой критерий: термодинамическая система находится в
равновесии, если при данной (постоянной) энтропии внутренняя энергия системы
минимальна, т. е. при
S = const. U = min, dU = 0 d
2
U > 0.
(2.22)
Наглядное графическое изображение
доказательства теоремы Гиббса приводит в
своей монографии Д. С. Коржинский.
Пусть мы имеем равновесное состояние
системы с S
I
и U
I
(рис. 2.1) где S
I
=max.
Допустим, что этому состоянию S
I
может отвечать
другое состояние системы с еще меньшей
энергией (точка S
I
U
II
), но тогда чтобы
повысить энергию системы до U
I
мы должны
сообщить системе тепло, что приведет к
увеличению ее энтропии до S
II
(точка S
II
U
I
).
Иначе говоря если возможно состояние S
I
U
II
,
то обязательно возможно состояние S
II
U
I
. Но это противоречит условию S
I
=max и
следовательно возможно одно единственное соотношение: если S=max (при U=const), то
U=m
I
n (при S=const).
Разберем условия равновесия термодинамических систем несколько подробнее.
Максимум энтропии как критерий равновесия характеризует изолированную систему,
которая окружена жесткой оболочкой (V=const), не пропускающей тепло (U=const) и
вещество
,
т. е. S = ƒ (U, V, m
a
... m
k
). Изолированные системы в природе не встречаются и
представляют термодинамическую абстракцию. Минимум внутренней энергии как
критерий равновесия относится уже к другой системе, называемой изохоро-
изоэнтропической, которая характеризуется постоянством энтропии объема и масс
компонентов, т. е. U = ƒ (S, V, m
a
... m
k
). Нетрудно представить, что те естественные
процессы, которые в изолированной системе приводили к возрастанию энтропии, в этой
системе могут осуществляться только путем отвода тепла от системы (так как энтропия ее
постоянна), что вызывает уменьшение внутренней энергии системы. В соответствии с
первым и вторым началами выражение внутренней энергии гомогенной, однофазовой
системы в состоянии равновесия имеет вид
(2.12)
Кроме этого уравнения, поскольку dU является полным дифференциалом, справедливы
соотношения (2.14, 2.15, 2.16):

Таким образом, в состоянии равновесия 2k+5 параметров, входящих в уравнение (2.12),
связаны k+3 уравнениями: одно уравнение (2.12) и k+2 уравнения (2.14)-(2.16). Это
означает что число независимых параметров или факторов состояния в однофазовой
системе равно f= (2k+5)-(k+3) =k+2 параметра. Факторами состояния рассматриваемой
системы являются S, V, m
a
...m
k
, и если при определенном (постоянном) значении их
внутренняя энергия как функция факторов состояния имеет минимальное значение,
система находится в равновесии.
Обратимся теперь к гетерогенной, многофазовой, изохоро-изоэнтропической системе.
Изменение внутренней энергии такой системы выразится, очевидно, как сумма изменений
внутренней энергии всех фаз системы от А до R, число которых равно r, т. е. как сумма r
уравнений вида (2.12):
Причем, согласно определению системы (S, V, m
a
...m
k
=const): т. е.
Выполнение условия равновесия системы U=min, или dU=0, d
2
U>0 возможно только при
таком состоянии системы, когда интенсивные параметры во всех фазах равны, т. е. при
условии
В справедливости уравнений (2.24) легко убедиться. Пусть температуры двух фаз или
частей системы не равны, например Т
А
> Т
В
. Тогда в системе, очевидно, будет
происходить естественный процесс переноса тепла от более нагретой фазы -δQ
A
= -T
A
dS к
менее нагретой +δQ
B
= T
B
dS, который приведет к уменьшению внутренней энергии
системы: dU = -T
A
dS + T
B
dS = (T
B
-T
A
)dS < 0. Иначе говоря, минимальное значение
внутренней энергии системы будет достигнуто в таком состоянии, когда температура во
всех фазах или частях системы станет одинаковой. Обратим внимание, что по мере
достижения равновесия система будет совершать <тепловую работу> (отдавать тепло) и
эта работа будет максимальной (поскольку dU-полный дифференциал).
Точно так же пусть, например, давление в одной фазе или части системы (А) будет
больше давления в другой фазе (В): р
А
> р
В
. В этом случае будет происходить увеличение
объема первой фазы (+p
А
dV) за счет уменьшения объема второй фазы (-p
В
BdV), в
результате чего внутренняя энергия системы будет уменьшаться: dU=-(р
А
dV-p
В
dV)=(p
В
-
р
А
)dV < 0. Ясно, что уменьшение внутренней энергии за счет механической работы будет
продолжаться до тех пор, пока давление во всех фазах или частях системы не станет
одинаковым, и это уменьшение внутренней энергии будет отражать максимальную
механическую работу системы.
Наконец, аналогичным образом легко показать, что если химический потенциал какого-
либо компонента в одной фазе больше, чем в другой, например μ
A
a
> μ
B
a
, то компонент из
фазы с большим химическим потенциалом будет переходить в фазу с меньшим
химическим потенциалом, а это приведет к уменьшению внутренней энергии cистемы: dU
= -μ
A
a
dm
a
+ μ
B
a
dm
a
= (μ
B
a
-μ
A
a
)dm
a
< 0. Очевидно также, что равенство химических
потенциалов компонентов по фазам отвечает минимальному значению внутренней
энергии системы, или, что то же, состоянию равновесия, а уменьшение внутренней
энергии при достижении равновесия выражает максимальную химическую работу
системы.
Таким образом, уравнения (2.24) определяют необходимые условия равновесия
гетерогенной, многофазовой, многокомпонентной системы. Их можно сформулировать
так: для того чтобы гетерогенная термодинамическая система находилась в
состоянии равновесия необходимо, чтобы интенсивные параметры во всех фазах
системы были равны. Обратим внимание на то, что это условие является необходимым,
но недостаточным критерием равновесия. Возможны такие состояния системы, когда
интенсивные параметры по всем фазам системы равны, но внутренняя энергия не является
минимальной, т. е. в системе, в принципе, осуществимы такие преобразования, которые
при данных значениях интенсивных параметров приведут к уменьшению внутренней
энергии системы. Такие состояния системы называются метастабильными.
Метастабильные состояния очень широко распространены в природных минеральных
системах, когда минеральные фазы и ассоциации, образованные при высоких
температурах и давлениях, сохраняются при низких температурах и давлениях, например
на поверхности Земли. Причина устойчивости метастабильных состояний - кинетическая,
еѐ следует рассматривать уже c позиций кинетики, а не термодинамики.
В отличие от метастабильных, полностью равновесное состояние, отвечающее
минимальной внутренней энергии при данных значениях факторов состояния,
обозначается как стабильное. Таким образом, равенство по фазам интенсивных
параметров - дополнительное необходимое условие равновесия многофазовых систем,
вытекающее для гетерогенных систем из единственного необходимого и достаточного
признака равновесия - минимума внутренней энергии (или максимума энтропии) при
определенных (постоянных) значениях факторов состояния системы.
Рассмотрим теперь вопрос о числе независимых параметров или факторов состояния в
многофазовых системах. Как было показано, однофазовая система в состоянии равновесия
определяется k+2 независимыми параметрами. В гетерогенной системе, состоящей из r
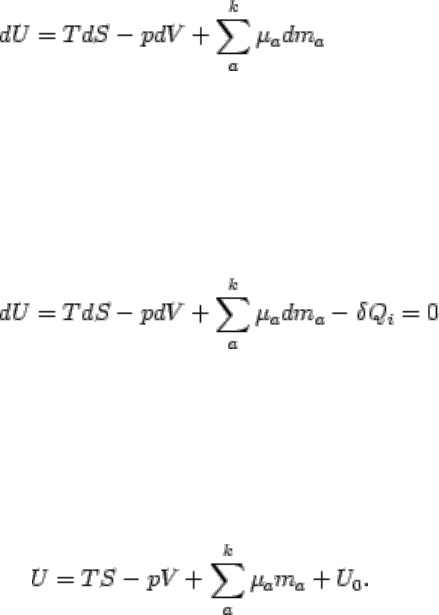
фаз, возможное число независимых параметров (k+2)r ограничено условиями равновесия
(2.24), т.е. (k+2)(r-1) уравнениями. Тогда число независимых параметров равно: ƒ = (k+2)r
- (k+2)(r-1) = k+2. Таким образом, состояние равновесной гетерогенной системы
полностью определяется k+2 независимыми параметрами, или факторами
состояния. Физическое содержание этого вывода легко пояснить, обратившись к табл.2.1:
если система находится в равновесии, т. е. U=min, dU=0, то каждая пара параметров,
характеризующих различные виды работ системы, сопряжена уравнением связи таким
образом, что только k+2 из них (по одному на каждый вид работ) могут изменяться
независимо, т. е. являться факторами состояния. Независимыми параметрами изохоро-
изоэнтропической системы, функция факторов состояния, или просто функция состояния,
которой - внутренняя энергия, являются энтропия, объем и массы компонентов (они
входят под знаком дифференциала в уравнения 2.12 и 2.23).
Термодинамические потенциалы
Продолжим рассмотрение внутренней энергии как функции состояния изохоро-
изоэнтропической системы. Поскольку в условиях равновесия значения интенсивных
параметров одинаковы во всех фазах системы, то уравнение (2.23) для равновесных
состояний может быть равносильно заменено уравнением (2.12):
(2.12)
которое справедливо и для гомогенных, и для гетерогенных равновесных систем.
Приведем еще одно самое общее выражение изменения внутренней энергии, где в
развернутой форме через факторы состояния выражено равновесное значение dU, а
членом δQ
i
- некомпенсированное тепло - суммарно обозначены необратимые изменения
dU по мере достижения равновесия:
(2.25)
Если система находится в равновесии δQ
i
= 0 и интенсивные параметры равны во всех
частях и в системе в целом, то уравнение изменения внутренней энергии (2.12) можно
интегрировать, принимая, что интенсивные параметры не зависят от сопряженных
экстенсивных. В результате получим
Проведенное интегрирование равносильно увеличению размера и соответственно
экстенсивных параметров системы: удвоению, утроению размеров ее части, переходу от
части к целому, от бесконечно малых к конечным. Очевидно, что при этой операции в
равновесной системе T, P, μ
a
...μ
k
могут рассматриваться как постоянные множители, а U
0
представляет константу интегрирования, зависящую от начального состояния системы, и
если принять его бесконечно малым по размерам и с ничтожным теплосодержанием, то U
0
~= 0. В дальнейшем изложении, как и принято в курсах термодинамики, эта константа
опущена и использовано следующее выражение интегральной внутренней энергии:
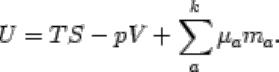
(2.26)
Подведем некоторые итоги рассмотрения свойств внутренней энергии. Выше было
показано, что внутренняя энергия: а) является функцией состояния системы и ее
дифференциал обладает свойствами полного дифференциала, б) становится минимальной
в состоянии равновесия, в) представляет собой характеристическую функцию в том
смысле, что производные этой функции по термодинамическим параметрам тоже
являются термодинамическими параметрами; г) изменение внутренней энергии равно
максимальной работе, которую совершает система по мере достижения состояния
равновесия. Функции, характеризующиеся совокупностью отмеченных свойств, являются
в термодинамике фундаментальными и носят специальное название -
термодинамические потенциалы. Приведем определение: термодинамическим
потенциалом называется характеристическая функция состояния системы, которая
убывает при всех необратимых процессах, производя при этом максимальную
работу, и становится минимальной в состоянии равновесия. Следовательно,
внутренняя энергия представляет таким образом, термодинамический потенциал изохоро-
изоэнтропической системы.
Выведем теперь термодинамические потенциалы других типов систем, различающихся по
набору факторов состояния, или, что то же, по характеру взаимодействия их с
окружающей средой. Ограничимся возможными вариациями факторов состояния,
характеризующих только тепловые и механические процессы. Обратившись к табл. 2.1,
нетрудно видеть, что кроме рассмотренной системы S, V, m
a
...m
k
в силу сопряженности
параметров можно предполагать существование только таких систем: T, V, m
a
...m
k
; S, p,
m
a
...m
k
; T, p, m
a
...m
k
. Каждая из этих систем отличается от изохоро-изоэнтропической
системы заменой одного или двух экстенсивных параметров, характеризующих тепловые
и механические процессы, на сопряженные интенсивные параметры. Всѐ эти типы систем
имеют реальное содержание, встречаются в природе и производственной практике и этим
прежде всего определяется целесообразность выявления особенностей систем, условия
существования которых выражаются заменой экстенсивных факторов состояния на
сопряженные интенсивные. Рассмотрим кратко физический смысл различных условий
существования систем и выведем их характеристические функции - термодинамические
потенциалы.
Обратимся сначала к изохро-изотермической системе с факторами состояния T, V, m
a
...m
k
.
В отличие от изохоро-изоэнтропической в рассматриваемой системе фактором состояния,
регулирующим тепловые процессы, служит температура, определяемая внешней по
отношению к системе средой. Одинаковая температура для всех частей этой системы
устанавливается не в результате достижения равновесия (как это было в
изоэнтропической системе), а предопределена заранее и всегда обеспечивается
физическими условиями существования системы. Следовательно, уменьшение
термодинамического потенциала в системе не может происходить за счет выравнивания
температур, и система не может производить <тепловую работу>. Тогда для того, чтобы
получить из внутренней энергии значение термодинамического потенциала изохоро-
изотермической системы, мы должны каким-то образом удалить (вычесть) из внутренней
энергии (уравнение 2.26) член, характеризующий тепловую работу системы.
Соответствующее корректное математическое преобразование замены одного параметра
на сопряженный носит название <преобразования Лежандра>, смысл его ясен из
нижеследующего.

Термодинамический потенциал изохоро-изотермической системы (в учебниках
термодинамики ее обычно обозначают сокращенно как изотермическую), называемый
свободной энергией Гельмгольца, или просто свободной энергией F=ƒ(T,V,m
a
...m
k
), равен:
Условия равновесия изохоро-изотермической системы F = ƒ(T, V, m
a
...m
k
) = min, dF = 0 и
d
2
F > 0, что непосредственно следует из уравнения (2.28). Легко показать, что для
равновесной гетерогенной изохоро-изотермической системы необходимо также равенство
по фазам давлений и химических потенциалов компонентов 3. Наконец, уменьшение
свободной энергии по мере достижения равновесия (-δQ
i
=dF< 0) представляет
максимальную (dF-полный дифференциал) полезную работу системы, слагающуюся из
собственно механической работы расширения и работы вследствие химических процессов
в системе.
Рассмотрим теперь изобаро-изоэнтропическую систему с факторами cостояния S, p,
m
a
...m
k
, которая характеризуется равенством давления во всех частях системы,
предопределенным условиями существования системы. Термодинамический потенциал
такой системы, рассуждая аналогично вышеизложенному, может быть получен путем
вычитания из внутренней энергии члена, характеризующего механическую работу
системы. Распространяя, таким образом, преобразование Лежандра на член - pV, получим
выражение термодинамического потенциала изобаро-изоэнтропической системы (ее
обозначают часто как изобарическую), который носит название энтальпии H = ƒ(S, p,
m
a
...m
k
):
(2.30)
Условием равновесия изобаро-изоэнтропической системы является минимум энтальпии:
H = ƒ (S, p, m
a
...m
k
) = min или dH = 0, d
2
H > 0. Для этого в гетерогенной системе
необходимо равенство по фазам температур и химических потенциалов компонентов, что
может быть показано аналогично рассмотренному выше (в примечаниях) для F-
потенциала. Факторы состояния ƒ
in
+ ƒ
ex
= 1 + (k+1) = k + 2. Изменение энтальпии dH
является полным дифференциалом и уменьшение H-потенциала по мере приближения к
состоянию равновесия будет характеризовать максимальную теплоотдачу системы: -δQ
i
=
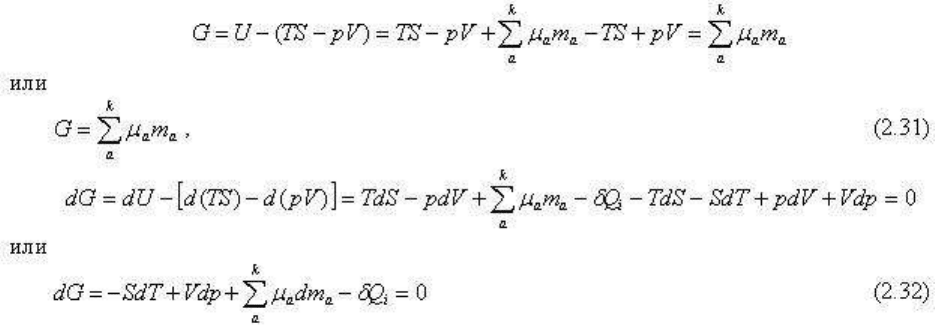
dH < 0. Поскольку H-система не может производить механическую работу, уменьшение
термодинамического потенциала происходит только путем отдачи тепла системой. За эти
свойства энтальпию нередко называют теплосодержанием.
Наконец, изотермо-изобарические системы характеризуются факторами состояния: G = ƒ
(T, p, m
a
...m
k
). В этих системах равенство по фазам температур и давлений задано
условиями существования системы, и, уменьшение термодинамического потенциала
(полезная работа системы) не может происходить за счет их выравнивания внутри
системы. Тогда, вычитая из внутренней энергии члены соответственно тепловой (TS) и
механический (pV) работы, получим выражение термодинамического потенциала
изотермо-изобарической системы, который носит название свободной энергии Гиббса,
потенциала Гиббса, изотермо-изобарического потенциала или собственно
термодинамического потенциала:
Очевидно, что аналогично рассмотренному выше условием равновесия изотермо-
изобарический системы является минимум термодинамического потенциала: G = ƒ (T, p,
m
a
...m
k
) = min, dG = 0 и d
2
G>0 для чего в гетерогенной системе должно выполняться
условие равенства химических потенциалов по всем фазам. Факторы состояния ƒ
in
+ ƒ
ex
=
2 + k = k + 2 (ƒ
in
= T, ƒ
ex
= m
a
...m
k
). Функция dG является полным дифференциалом и
изменение свободной энергии Гиббса (G-потенциала) характеризует максимальную
работу химических процессов, поскольку система не может производить ни механической
работы, ни передачи тепла.
Сопоставляя уравнения (2.26), (2.27), (2.29) и (2.23), можно получить соотношения между
четырьмя основными характеристическими функциями:
G = U - TS - (-pV) = H - TS = F - (-pV)
(2.33)
где, очевидно, F=U-TS и H=U+pV.
Все термодинамические
потенциалы являются
экстенсивными параметрами и
имеют размерность энергии (так
же, как и каждое произведение
интенсивного параметра на
соответствующий экстенсивный).
Функции Н и U носят в
термодинамике названия тепловых
функций (что по отношению к U
недостаточно, так как в равной
мере U отражает и работу
системы). Из соотношения
H=U+pV следует что δQ
p
> δQ
V
(где δQ
p
=δH и δQ
V
=δU), т. е. тепло,
полученное (отданное) системой в
изобарических условиях, всегда
больше изохорического теплового
эффекта. Из соотношения F=U-TS
следует уже обсуждавшееся выше
заключение о том, что
максимальная полезная работа
системы всегда меньше ее
внутренней энергии, часть которой
в системе T, V, m идет на
возрастание энтропии системы (из
выражения (2.28) можно
убедиться, что увеличение S
уменьшает F). Максимальная
полезная работа изотермической
системы складывается из собственно работы расширения δА
V
и работы химических
процессов в системе δА
W
, которые имеют как уже отмечалось, разные знаки, т.е. δА
T
= -
dF = δА
V
- δА
W
. Свободная энергия Гиббса G характеризует химическую энергию
системы. Изменение G отражает тепловые и объемные эффекты химических процессов в
системе, которые протекают (при данных Т и р) в направлении увеличения энтропии и
уменьшения объема системы (что, согласно выражению (2.32), приведет к уменьшению
G). Сопоставление G=F+pV=Н-TS показывает что химическая энергия системы также не
может быть полностью реализована в виде полезной работы, часть ее обязательно будет
рассеяна, т. е. израсходована на возрастание энтропии системы.
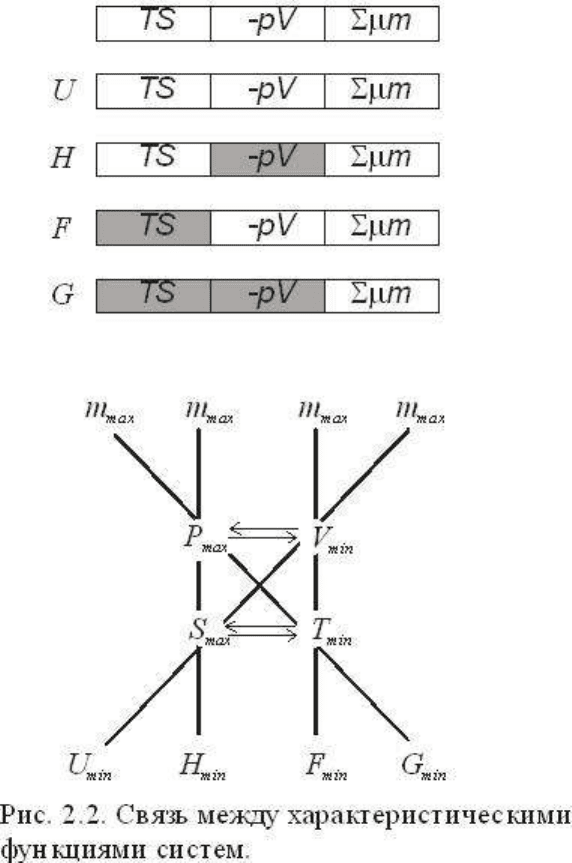
Рассмотренные соотношения между термодинамическими потенциалами графически
изображены в верхней части рис.2.2. В нижней части показаны экстремальные значения
(максимум и минимум) факторов состояния (они соединены линиями) и сопряженных
параметров (показали стрелками) в условиях равновесия и максимальной работы для
каждого типа систем. Доказательства соответствующих экстремумов непосредственно
следуют из уравнений термодинамических потенциалов и легко могут быть выражены,
используя их свойства полных дифференциалов, через частные производные по факторам
состояния. Так, для U = ƒ (S, V, m):
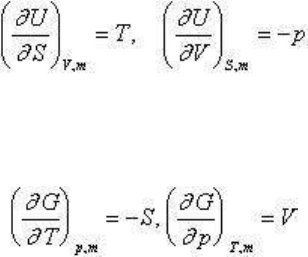
и минимальному значению U будет отвечать минимум T и максимум p. Для системы G = ƒ
(T, p, m),
и минимальному значению свободной энергии G будет отвечать максимум S и минимум p,
и аналогично для всех систем. Свойство термодинамических потенциалов как полных
дифференциалов широко используется в термодинамике для анализа самых
разнообразных термодинамических зависимостей.
Рассмотренные термодинамические потенциалы как характеристические функции
состояния систем были выведены во второй половине прошлого века Ф. Массье и Дж.
Гиббсом, а принятый нами метод изложения от исходных начал термодинамики через
термодинамические потенциалы как общие функции состояния и далее к частным
выводам обозначается обычно как метод Гиббса, поскольку им впервые термодинамика
была изложена дедуктивно в самом общем виде. Этот метод изложения, к сожалению, не
получил широкого признания, по-видимому, в основном потому, что соответствующие
математические выводы не сопровождались достаточным истолкованием физического
смысла операций. Термодинамика по-прежнему излагается как совокупность множества
эмпирических соотношений, хотя в конце всех полных курсов приводится характеристика
метода Гиббса (Герасимов и др., 1963; Базаров, 1961; и др.). В полной мере метод Гиббса
использован только в работах Э. Гугенгейма (1941, 1950), В. Шоттки и др. (Schottky et а1.,
1929) и Д. С. Коржинского (1957, 1972), в какой-то мере в курсе А. Мюгстера (1971). Мы
сознательно следовали в выводе термодинамических потенциалов ближе всего изложению
Д. С. Коржинского, опустив при этом подробные математические выкладки и еще более
усилив рассмотрение физического смысла операций.
Общие критерии равновесия и термодинамические потенциалы, число независимых
параметров и правило фаз
Обратимся еще раз, на новом уровне, к обсуждению условий равновесия
термодинамических систем. Можно сформулировать следующее самое общее положение:
термодинамическая система находится в равновесии, если при данных определенных
факторах состояния термодинамический потенциал ее имеет минимальное значение, или,
короче, - необходимым и достаточным условием равновесия любой термодинамической
системы является минимум ее термодинамического потенциала, т. е.
Ф=min, dФ=0, d
2
Ф>0.
(2.34)
Как было показано выше, выполнение этого условия в гетерогенной системе требует
равенства интенсивных параметров по всем фазам системы. Наконец, из этого условия
обязательно следует что если система находится в равновесии, то ее состояние полностью
характеризуется k+2 независимыми параметрами, которые, как отмечалось, обычно
называют факторами состояния, или факторами равновесия. Указанные положения были
доказаны для изохоро-изоэнтропической системы, но они полностью распространяются и
на все другие типы систем. Правомерность этого непосредственно следует из тех
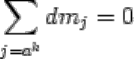
ограничений, которые наложены на условия существования других рассмотренных типов
систем и может быть строго доказана для каждой системы независимо.
Представление о термодинамическом равновесии относится к фундаментальным
понятиям термодинамики, и правильное понимание его как бы предопределяет
возможности использования термодинамических методов. В связи с этим необходимо
обсудить еще несколько вопросов.
Во многих курсах термодинамики при выводе термодинамических потенциалов
используется представление о закрытых системах, т.е. априори принимается
dm
a
=dm
b
=...=dm
k
=0 и термодинамические потенциалы рассматриваются без члена,
характеризующего химическую энергию (например, dU=TdS-PdV,
dH=dU+d(pV)=TdS+Vdp и т. д.). Строго говоря, это, конечно, неправильно, поскольку
выражение химической энергии компонентов входит во все термодинамические
потенциалы и уменьшение термодинамического потенциала вследствие уменьшения
химической энергии может происходить во всех системах, в том числе и в закрытых,
которые не обмениваются компонентами с окружающей средой.
Общепринято также рассматривать условия равновесия применительно к изолированным
и затем к закрытым системам. Однако критерии равновесия никак не связаны с условиями
изоляции систем от окружающей среды. Поясним это следующим логическим опытом.
Выделим в пределах равновесной системы (система А) какую-либо часть ее (новая
система В), также, естественно, находящуюся в состоянии равновесия. Если систему В
заключить в непроницаемую для вещества оболочку, то состояние системы от этого никак
не изменится, она будет продолжать находиться в равновесии, так как условие
входит в определение равновесной системы. Если же система В, заключенная в
непроницаемую для вещества оболочку, находится в состоянии равновесия и в равновесии
с системой А (т. е. при тех же значениях интенсивных параметров), то состояние ее не
изменится, если снять изолирующую оболочку, так как при данных значениях факторов
состояния равновесное состояние является единственно стабильным, поскольку
характеризуется минимальным значением термодинамического потенциала. Таким
образом, сформулированные условия равновесия полностью распространяются и на
открытые системы, на что было указано еще Д. Гиббсом. Более того, как увидим ниже,
условия той или иной изоляции накладывают дополнительные ограничения на системы,
никоим образом не вытекающие из критериев равновесия, которые справедливы для всех
систем, в том числе и для открытых систем.
Еще одно очень существенное дополнение. При рассмотрении состояния равновесия было
принято, что факторы состояния систем являются постоянными. Этот традиционный в
термодинамике подход увековечен названиями систем: изотермическая, изобарическая и
т. д. (где приставка <изо> по-гречески означает постоянный). Такой прием дает
возможность установить и охарактеризовать условия равновесия наиболее простым и
ясным способом. Однако выявив таким образом признаки и критерии равновесия, можно
показать, что постоянство факторов состояния не является обязательным условием
равновесия. Действительно, пусть k+2 независимых параметров, определяющих состояние
системы, не являются постоянными, а находятся в процессе изменения. Пусть при этом
процессы в системе осуществляются таким образом, что в каждый данный момент все
другие параметры системы полностью определяются k+2 факторами состояния, а
термодинамический потенциал как функция факторов состояния в каждый данный
