Zelditch M.L. (и др.) Geometric Morphometrics for Biologists: a primer

Подождите немного. Документ загружается.

chap-06 4/6/2004 17: 23 page 148

148 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

at the ith landmark is denoted (X



, Y



V =





















(

, Y

)

(

, Y

)

(

, Y

)

(

, Y

)

(

, Y

)

(

, Y

)







= LW (6.46)

where LW is the product of two matrices L and W. L is the (K +3) ×(K +3) matrix:

L =







(

)



1, 2





1, 3



··· U



1, K



1 X



2, 1



(

)



2, 3



··· U



2, K



1 X



3, 1





3, 2



(

)

··· U



3, K



1 X



K,1





K,2





K,3



··· U



K, K



1 X

111··· 1000

··· X

00 0

··· Y

00 0







(6.47)

in which U(R) is the function appearing in Equations 6.44 and 6.45 evaluated at each

landmark location (X

, Y

). W is the (K +3) ×2 matrix of weights and uniform terms

appearing in Equations 6.44 and 6.45:

W =













(6.48)

So we have the equation:

V = LW (6.49)

in which L and W are the matrices just described. We wish to solve for W, the matrix of

coefficients in our spline model, which gives us:

W = L

−1

V (6.50)

We can use the weights in the matrix W in conjunction with the spline functions in Equa-

tions 6.44 and 6.45 to interpolate the observed deformation at the landmarks over the

entire specimen. However, it turns out that we can make some further use of the matrix

−1

. This matrix is (K +3) by (K +3); if we take the first K rows and the first K columns

of L

−1

, we can form L

−1

, which is called the bending energy matrix.

chap-06 4/6/2004 17: 23 page 149

THE THIN-PLATE SPLINE 149

The bending energy matrix can be rearranged into a series of eigenvectors E

, and

eigenvalues, λ

, such that:

−1

= λ

(6.51)

The eigenvectors E

have the usual properties of eigenvectors, and consequently they are a

basis (or a set of coordinate axes) of a space. In this case, the eigenvectors are the basis of

the Euclidean space tangent to shape space at the reference shape. This means that we can

express our matrix of observed deformations V as a linear combination of the eigenvectors

of the bending energy matrix. The eigenvalues are the bending energies required to effect

a change (of a given amount of shape difference, i.e. a unit of Procrustes distance) at that

spatial scale.

Three of the eigenvalues of the bending energy matrix are zero, corresponding to the

components with no bending (with X- and Y-coefficients, these eigenvectors account for

the six uniform components of the deformation). The remaining K −3 eigenvectors are

the explicitly localized components of a deformation. These eigenvectors are called the

partial warps; the vector multipliers of the partial warps are called the partial warp scores

(following Slice et al., 1996). They are “partial” because they describe part of a deforma-

tion. We should note that Bookstein (1991) called the eigenvectors of the bending energy

matrix principal warps, analogous to principal components. By “partial warp,” he meant

the vector multiple of a principal warp. Slice and colleagues use the term principal warp

to refer to a partial warp interpreted as a bent surface of the thin-plate spline, and because

the latter terminology has become standard, we use it here.

As evident in the definition of L

−1

, only one matrix of landmarks enters into the cal-

culation of bending energy; the coordinates of the form usually called the reference or

starting form. Thus, the eigenvectors that give us a coordinate system for shape analy-

ses are a function of one single form. This may be highly counterintuitive, because more

familiar eigenvectors, such as principal components, are functions of an observed variance–

covariance matrix. They are functions of variation (or differences) among observed forms.

That is not the case for the eigenvectors of the bending energy matrix. The eigenvalues

of the bending energy are the bending energies that would be required to modify a given

shape by a single unit of shape difference at each spatial scale. Thus the partial warps are

not themselves features of shape change, they are simply a coordinate system or basis for

the space in which we analyze shape change.

The “A” coefficients in Equation 6.48 describe the uniform deformation of the shape.

There are six of these coefficients, which is enough to describe the six components of the

uniform deformation of shape. However, we know that the reference and the target do

not differ by rotation, rescaling or translation, because those differences were removed by

the superimposition process. Consequently, we do not need six parameters to describe the

uniform component of the deformation, only the two components derived earlier in this

chapter.

By convention, partial (or principal) warps are numbered from the lowest to highest

bending energy; the one with the highest number corresponds to the one with greatest bend-

ing energy. The two uniform components are sometimes called the zero

principal warp.

Thinking of the uniform components in those terms is useful because it emphasizes that the

uniform components cannot be viewed separately from the non-uniform ones. Including

chap-06 4/6/2004 17: 23 page 150

150 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

the uniform terms also completes the tally of shape variables. The K −3 partial warps

contribute 2K −6 scores; adding the two uniform scores brings the count up to 2K −4.

Using the thin-plate spline to visualize shape change

The combination of the uniform and non-uniform components completely describes any

shape change. The set of partial warp scores (including scores on the uniform component)

can be used in any conventional statistical analysis and, like the coordinates obtained by

GLS, the sum of their squares equals the squared Procrustes distance from the reference.

Moreover, like Bookstein’s shape coordinates, they have the correct degrees of freedom.

Thus we can use partial warps in any statistical procedure, such as regression, and diagram

the results as a deformation.

Interpreting changes depicted by the thin-plate spline

Interpretations should be presented in terms of the total deformation, not by detailing the

separate uniform and non-uniform components (or the more finely subdivided components

of them). Just as we cannot talk about individual landmarks as if they were separately

moved, we cannot talk about components of the total deformation as if they were separate

parts of the whole. It is important to remember that the changes depicted are based on

an interpolation function – we do not actually know what occurs between landmarks. If

we have sparsely sampled some regions of the body, we cannot assume that the spline

provides a realistic picture of their changes; there might be many highly localized changes

that cannot be detected in the absence of closely spaced landmarks. All we can say is that

our data do not require any more localized changes.

We cannot show an example of a biological transformation depicted by the thin-plate

spline until we have results to show, so we will borrow examples from a later chapter

(Chapter 10) to discuss the description of shape change using the thin-plate spline. In

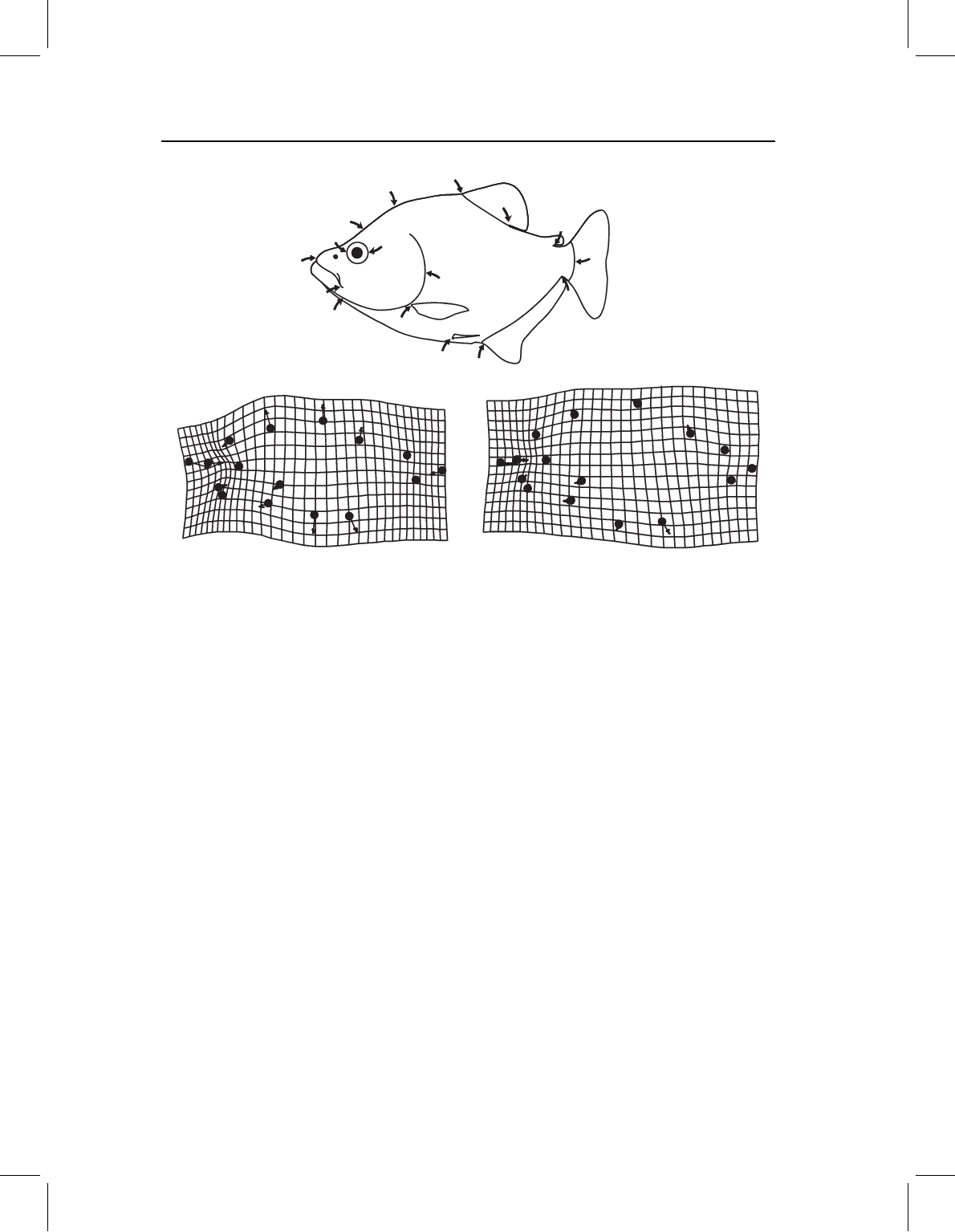
Figure 6.7 we depict the ontogenetic changes in body shape of two species of piranhas:

S. gouldingi (Figure 6.7A), which we used earlier in this chapter, and Pygopristis denticulata

(Figure 6.7B). In both species the head (as a whole) grows less rapidly than the middle of

the body, and the eye grows far more slowly than the head. In neither species does the

shortening of the eye result solely from the generally lower cranial growth rates; rather,

there is an abrupt (and localized) deceleration of growth rates in the orbital region. How-

ever, that does not, by itself, fully account for the apparent contraction of the grid in the

head, especially in S. gouldingi. Part of the relative shortening of the head, supraorbitally,

results from the displacement of the landmark at the epiphyseal bar (landmark 2) towards

the anterior landmark of the eye (landmark 14). Suborbitally, the apparent shortening

of the head results from the displacement of the posterior jaw landmark (landmark 13)

towards the posterior eye landmark (landmark 15), as well as from the more general short-

ening of the snout and eye. These two species also differ in the ontogeny of posterior body

shape. In S. gouldingi, the caudal peduncle (the region bounded by landmarks 6, 7, and

8) appears to contract, but no change appears to be localized there – the posterior body

generally shortens (as does the head). Growth rates appear to decrease, moving posteriorly

from the midbody to the tail. Because the caudal peduncle is the most posterior part of

the body, the growth rates are lowest there. In P. denticulata, growth rates decrease more

chap-06 4/6/2004 17: 23 page 151

THE THIN-PLATE SPLINE 151

(A) (B)

Figure 6.7 Ontogenetic shape change for two species of piranhas: (A) Serrasalmus gouldingi;

(B) Pygopristis denticulata.

slightly, and most of the change in the posterior body seems to result from the posterior

displacement (and relative shortening) of the anal fin. That increases the distance between

the pelvic and anal fins (which expands the grid between them), but because that is not a

part of the general expansion of the midbody (it is limited to the ventral region between

the fins) the change is ventrally localized. Due to the sparse sampling of landmarks in the

middle of the body, there is no abrupt contraction or expansion of the grid such as we see

in the head. Sparse sampling of that region makes it difficult to detect localized changes

because we cannot show what happens between landmarks when we have not sampled

them (quoting Gertrude Stein, “there is no there there”).

Software

Until we have results to depict, the spline serves the purpose of providing variables, with

the correct degrees of freedom, for statistical analysis. A file of partial warps, along with

the uniform components, can be computed by several programs in the IMP software series,

all of which output the data in a form that can be input into statistical packages (i.e. they

are in the X1,Y1,…CS format). They are perhaps most easily obtained from the Principal

Components Analysis program (PCAGen, discussed in Chapter 7), which calculates partial

warps relative to the mean shape (that is, the mean serves as the reference form). Within

that software, as in all the others, the explicit uniform terms are always calculated using the

partial Procrustes superimposition (meaning that centroid size is fixed to one). To draw the

chap-06 4/6/2004 17: 23 page 152

152 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

deformations in different registrations, the software simply calculates the implicit uniform

deformations corresponding to the desired method of depicting the shape change. We will

return to this when we have results to depict.

References

Bookstein, F. L. (1989). Principal warps: thin-plate splines and the decomposition of deformations.

IEEE Transactions on Pattern Analysis and Machine Intelligence, 11, 567–585.

Bookstein, F. L. (1991). Morphometric Tools for Landmark Data: Geometry and Biology.

Cambridge University Press.

Bookstein, F. L. (1996). Standard formula for the uniform shape component in landmark data. In

Advances in Morphometrics (L. F. Marcus, M. Corti, A. Loy et al., eds) pp. 153–168. Plenum

Press.

Dryden, I. L. and Mardia, K. V. (1998). Statistical Shape Analysis. John Wiley & Sons.

Myers, P., Lundrigan, B. L., Gillespie, B. W. and Zelditch, M. L. (1996). Phenotypic plasticity in

skull and dental morphology in the prairie deer mouse (Peromyscus maniculatus bairdii). Journal

of Morphology, 229, 229–237.

Slice, D. E., Bookstein, F. L., Marcus, L. F. and Rohlf, F. J. (1996). Appendix I: A glossary for

geometric morphometrics. In Advances in Morphometrics (L. F. Marcus, M. Corti, A. Loy et al.,

eds) pp. 531–551. Plenum Press.

Thompson, D’Arcy W. (1942). On Growth and Form: A New Edition. Cambridge University Press.

(Reprinted in 1992 as On Growth and Form: The Complete Revised Edition, Dover Publications.)

chap-07 4/6/2004 17: 24 page 153

PART

Analyzing Shape Variables

chap-07 4/6/2004 17: 24 page 154

chap-07 4/6/2004 17: 24 page 155

Ordination methods

In this chapter, we discuss two methods for describing the diversity of shapes in a sam-

ple: principal components analysis (PCA) and canonical variates analysis (CVA). Our

discussion of these methods draws heavily on expositions presented by Morrison (1967),

Chatfield and Collins (1980), and Campbell and Atchley (1981). Both methods are used to

simplify descriptions rather than to test hypotheses. PCA is a tool for simplifying descrip-

tions of variation among individuals, whereas CVA is used for simplifying descriptions

of differences between groups. Both analyses produce new sets of variables that are lin-

ear combinations of the original variables. They also produce scores for individuals on

those variables, and these can be plotted and used to inspect patterns visually. Because

the scores order specimens along the new variables, the methods are called “ordination

methods.” It is hoped that the ordering provides insight into patterns in the data, per-

haps revealing patterns that are convenient for addressing biological questions. The most

important difference between PCA and CVA is that PCA constructs variables that can

be used to examine variation among individuals within a sample, whereas CVA con-

structs variables to describe the relative positions of groups (or subsets of individuals) in

the sample.

We discuss PCA and CVA in the same chapter because both serve a similar purpose,

and because the mathematical transformations performed in the two analyses are similar.

We describe PCA first because it is somewhat simpler, and because it provides a founda-

tion for understanding the transformations performed in CVA. We begin the description

of PCA with some simple graphical examples, and then present a more formal exposi-

tion of the mathematical mechanics of PCA. This is followed by a presentation of an

analysis of a real biological data set. The description of CVA follows a similar outline;

the only difference is that we begin with a discussion of groups and grouping variables.

CVA requires that the individuals be grouped, because the method analyzes the relative

positions of groups in the sample. Consequently, the sample must be divided into groups

before the analysis begins. The analysis of groups requires a few more computational steps

than PCA, but none of the steps in CVA introduce new mathematical concepts. CVA

will be just a new application of ideas you have already encountered in the discussion

of PCA.

ISBN 0–12–77846–08 All rights of reproduction in any form reserved

chap-07 4/6/2004 17: 24 page 156

156 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

Principal components analysis

Geometric shape variables are neither biologically nor statistically independent. For exam-

ple, the shape variables produced by the thin-plate spline describe variation in overlapping

regions of an organism or structure. Because the regions overlap, they are under the influ-

ence of the same processes that produce variation; and therefore we expect them to be

correlated. Even when they do not describe overlapping regions, morphometric variables

(both geometric and traditional) are expected to be correlated because they describe fea-

tures of the organism that are functionally, developmentally or genetically linked. Their

patterns of variation and covariation are often complex and difficult to interpret. The pur-

pose of PCA is to simplify those patterns and make them easier to interpret by replacing the

original variables with new ones (principal components, PCs) that are linear combinations

of the original variables and independent of each other.

One might wonder why it would be a worthwhile exercise to take simple variables that

covary with each other and replace them with complex variables that do not covary. Part

of the value of this exercise arises from the fact that the new complex variable is a function

of the covariances among the original variables. It thus provides some insight into the

covariances among variables that can direct future research into the identity of the causal

factors underlying those covariances. Another useful purpose served by PCA is that most

of the variation in the sample usually can be described with only a few PCs. Again this is

useful, because it simplifies and clarifies what needs to be explained. Another important

benefit of PCA is that the presentation of results is simplified. It is much easier to produce

and explain plots of the three PCs that explain 90% of the variation than it is to separately

plot and explain the variation on each of 30 original variables.

An indirect benefit of PCA that is useful (but often misused) is that it simplifies the

description of differences among individuals. Clusters of individuals are often more appar-

ent in plots of PCs than in plots of the original variables. Finding such clusters can be quite

valuable, but those clusters do not represent evidence of statistically distinct entities. Legit-

imate methods for testing the hypothesis that a priori groups are statistically significantly

different will be presented in Chapters 8 and 9 (computer-based statistical methods and

multivariate analysis of variance, respectively).

Geometric description of PCA

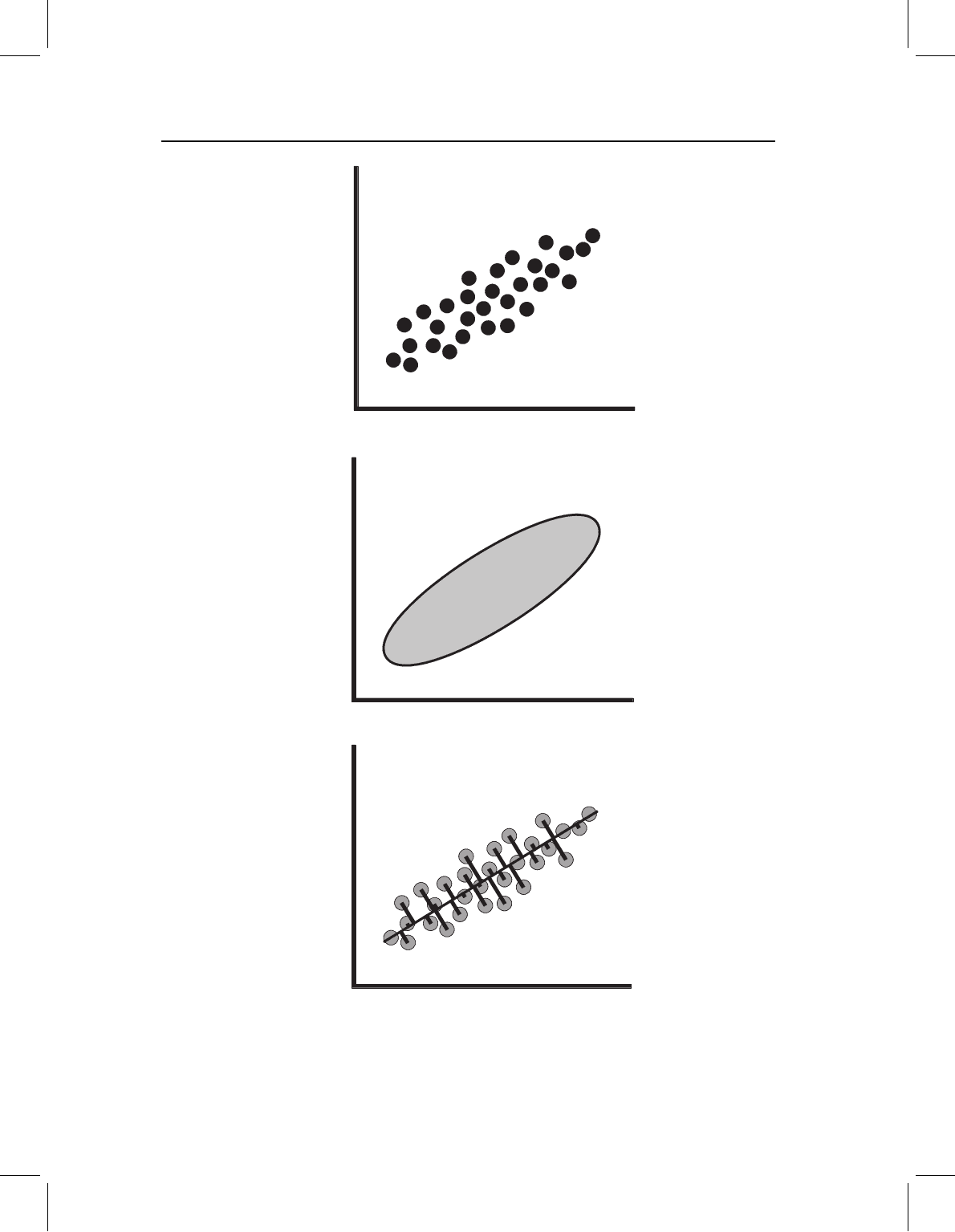
Figure 7.1A shows the simple case in which there are two observed traits, X

and X

These traits might be two distance measurements or the coordinates of a single landmark

in a two-dimensional shape analysis. Each point in the scatter plot represents the paired

values observed for a single specimen. We expect that the values of each trait are normally

distributed, and we expect that one trait is more variable than the other because one

variable, (in this case, X

) has a larger range of observed values and a higher variance. In

addition, the values of X

and X

are not independent; higher values of one are associated

with higher values of the other. This distribution of values can be summarized by an ellipse

that is tilted in the X

, X

coordinate plane (Figure 7.1B). PCA solves for the axes of this

ellipse, and uses those axes to describe the positions of individuals within that ellipse.

The first step of PCA is to find the direction through the scatter that describes the

largest proportion of the total variance. This direction, the long axis of the ellipse, is the

chap-07 4/6/2004 17: 24 page 157

ORDINATION METHODS 157

(A)

(B)

(C)

Figure 7.1 Graphical representation of the problem to be solved by PCA. (A) Scatter plot of indi-

viduals scored on two traits, X

and X

; (B) an ellipse enclosing the scatter of points shown in part

(A); (C) a line through the scatter and the perpendicular distances of the individuals from that axis.

The goal of PCA is to find the line that minimizes the sum of those squared distances.