Zelditch M.L. (и др.) Geometric Morphometrics for Biologists: a primer

Подождите немного. Документ загружается.

chap-07 4/6/2004 17: 24 page 158

158 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

(A)

(B)

(C)

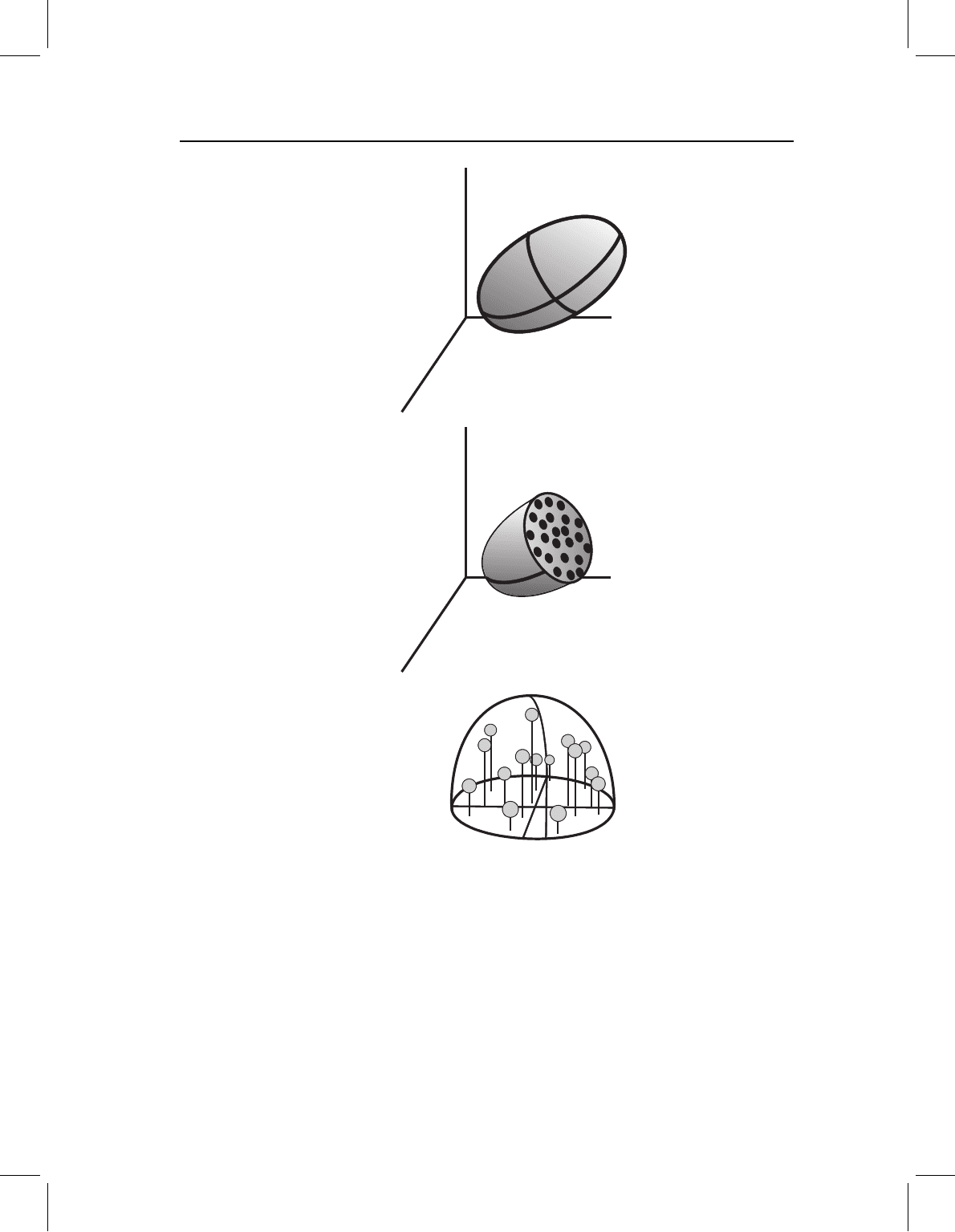
Figure 7.2 Graphical representation of PCA on three original variables (X

, X

). (A) The

distribution of individual specimens on the three original axes is summarized by a three-dimensional

ellipsoid; (B) the three-dimensional ellipsoid is cut by a plane passing through the sample centroid

and perpendicular to the longest axis (PC1) at its midpoint, showing the distribution of individuals

around the longest axis in the plane of the section; (C) the upper half of the ellipsoid in B has been

rotated so that the cross-section is in the horizontal plane. Perpendicular projections of all individuals

(from both halves) onto this plane are used to solve for the second and third PCs.

first principal component (PC1). In an idealized case like that shown in Figure 7.1A, the line

we seek is approximately the line through the two cases that have extreme values on both

variables. Real data rarely have such convenient distributions, so we need a criterion that

has more general utility. If we want to maximize the variance that the first axis describes,

chap-07 4/6/2004 17: 24 page 159

ORDINATION METHODS 159

then we also want to minimize the variance that it does not describe – in other words, we

want to minimize the sum of the squared distances of points away from the line (Figure

7.1C). (Note: the distances that are minimized by PCA are not the distances minimized in

conventional least-squares regression analysis – see Chapter 10.)

The next step is to describe the variation that is not described by PC1. When there are

only two original variables this is a trivial step; all of the variation that is not described by

the first axis of the ellipse is completely described by the second axis. So, let us consider

briefly the case in which there are three observed traits: X

, X

and X

. This situation is

unlikely to arise in optimally superimposed landmark data, but it illustrates a generalization

that can be applied to more realistic situations. As in the previous example, all traits

are normally distributed and no trait is independent of the others. In addition, X

has

the largest variance and X

has the smallest variance. A three-dimensional model of this

distribution would look like a partially flattened blimp or watermelon (Figure 7.2A). Again

PC1 is the direction in which the sample has the largest variance (the long axis of the

watermelon), but now a single line perpendicular to PC1 is not sufficient to describe the

remaining variance. If we cut the watermelon in half perpendicular to PC1, the cross-

section is another ellipse (Figure 7.2B). The individuals in the section (the seeds in the

watermelon) lie in various directions around the central point, which is where PC1 passes

through the section. Thus, the next step of the PCA is to describe the distribution of data

points around PC1, not just for the central cross-section, but also for the entire length of

the watermelon.

To describe the variation that is not represented by PC1, we need to map, or project,

all of the points onto the central cross-section (Figure 7.2C). Imagine standing the halved

watermelon on the cut end and instantly vaporizing the pulp so that all of the seeds drop

vertically onto a sheet of wax paper, then repeating the process with the other half of

the watermelon and the other side of the paper. The result of this mapping is a two-

dimensional elliptical distribution similar to the first example. This ellipse represents the

variance that is not described by PC1. Thus, the next step of the three-dimensional PCA

is the first step of the two-dimensional PCA – namely, solving for the long axis of a

two-dimensional ellipse, as outlined above. In the three-dimensional case, the long axis

of the two-dimensional ellipse will be PC2. The short axis of this ellipse will be PC3, and

will complete the description of the distribution of seeds in the watermelon. By logical

extension, we can consider N variables measured on some set of individuals to represent

an N-dimensional ellipsoid. The PCs of this data set will be the N axes of the ellipsoid.

After the variation in the original variables has been redescribed in terms of the PCs, we

want to know the positions of the individual specimens relative to these new axes (Figure

7.3). As shown in Figure 7.3A, the values we want are determined by the orthogonal pro-

jections of the specimen onto the PCs. These new distances are called principal component

scores. Because the PCs intersect at the sample mean, the values of the scores represent

the distances of the specimen from the mean in the directions of the PCs. In effect, we are

rotating and translating the ellipse into a more convenient orientation so we can use the

PCs as the basis for a new coordinate system (Figure 7.3B). The PCs are the axes of that

system. All this does is allow us to view the data from a different perspective; the positions

of the data points relative to each other have not changed.

As suggested by Figure 7.4, we could compute an individual’s score on a PC from the

values of the original variables that were observed for that individual and the cosines of

chap-07 4/6/2004 17: 24 page 160

160 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

(A) (B)

PC2

PC1

PC2

PC1

Figure 7.3 Graphical interpretation of PC scores. (A) The star is the location of an individual in

the sample. Perpendiculars from the star to PCs indicate the location of the star with respect to those

axes. The distances of points S

and S

from the sample centroid (intersection of PC1 and PC2)

are the scores of the star on PC1 and PC2. (B) The figure in part A has been rotated so that PCs

are aligned with the edges of the page. The PCs will now be used as the reference axes of a new

coordinate system; the scores on these axes are the location of the individual in the new system. The

relationships of the PC axes to the original axes has not changed, nor has the position of the star

relative to either set of axes.

PC2

PC1

Figure 7.4 Graphical interpretation of PC scores, continued. The angles α

and α

indicate the

relationship of PC1 to the original axes X

and X

. Thus, S

can be computed from the coordinates

of the star on X

and X

and the cosines of the angles between PC1 and the original axes. S

can be

computed from the coordinates of the star on X

and X

and the cosines of the angles between PC2

and the original axes.

chap-07 4/6/2004 17: 24 page 161

ORDINATION METHODS 161

the angles between the original variables and the PCs. In our simple two-dimensional case,

the new scores, Y, could be calculated as:

= A

(7.1)

where A

and A

are the cosines of the angles α

and α

and the values of individuals

on X

and X

are the differences between them and the mean, not the observed values of

those variables.

It is important to bear in mind for our algebraic discussion that Equation 7.1 represents a

straight line in a two-dimensional space. Later we will see equations that are expansions of

this general form and represent straight lines in spaces of higher dimensionality. So, in case

the form of Equation 7.1 is unfamiliar, the next few equations illustrate the simple conver-

sion of this equation into a more familiar form. First, we rearrange the terms to solve for X

−A

= A

(7.2)

=−A

(7.3)

−A

(7.4)

Then we make two substitutions (M =−A

and B =Y

) to produce:

= MX

+B (7.5)

Thus the formula for the PC is, indeed, the formula for a straight line.

Algebraic description of PCA

We begin this description of PCA by repeating the starting conditions and the constraints

we want to impose on the new variable. We have a set of observations of P traits on N

individuals, where P is the number of shape variables (not the number of landmarks). The

data comprise P variances and P(P −1)/2 covariances in the sample. We want to compute a

new set of P variables (PCs) with variances that sum to the same total as that computed from

the variances and covariances of the original variables, and we also want the covariances

of all the PCs to be zero. In addition, we want PC1 to describe the largest possible portion

of variance, and we want each subsequent PC to describe the largest possible portion of

the variation that was not described by the preceding components.

The full set of observations can be written as the matrix X:

X =







... X







(7.6)

where X

is the value of the Pth coordinate in the Nth individual. We can also think of

this as a P-dimensional space with N points plotted in that space – just a multi-dimensional

version of the simplistic examples presented in the previous section.

chap-07 4/6/2004 17: 24 page 162

162 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

Our problem is to replace the original variables (X

, X

, ...X

), which are the

columns of the data matrix, with a new set of variables (Y

, Y

, ...Y

), the PCs

that meet the constraints outlined in the first paragraph of this section. Each PC will be a

straight line through the original P-dimensional space, so we can write each Y

as a linear

combination of the original variables:

= A

+···+A

(7.7)

which can be expressed in matrix notation as:

= A

X (7.8)

where A

is a vector of constants {A

, A

...A

}. (The notation A

refers to the

transpose, or row form, of the column matrix A

.) All this means is that the new values of

the individuals, their PC scores, will be computed by multiplying their original values (listed

in matrix X) by the appropriate values A

of and summing the appropriate combinations

of multiples. Now we can see that our problem is to find the values of A

that satisfy the

constraints outlined above.

The first constraint we will address is the requirement that the total variance is not

changed. Variance is the sum of the squared distances of individuals from the mean, so

this is equivalent to requiring that distances in the new coordinate system are the same as

distances in the original coordinate system. The total variance of a sample is given by the

sample variance–covariance matrix S:

S =







... s







(7.9)

in which s

is the sample variance observed in variable X

, and s

(which is equal to s

)is

the sample covariance observed in variables X

and X

We can meet the requirement that the total variance is unchanged by requiring that each

PC is a vector of length one. If we multiply matrix X by a vector of constants as indicated

in Equation 7.8, the variance of the resulting vector Y

will be:

Var(Y

) = Var





= A

(7.10)

Thus the constraint that variance is unchanged can be formally stated as the requirement

that the inner product or dot product of each vector A

with itself must be one:

= 1 =



k=1

(7.11)

This means that the sum of the squared coefficients will be equal to one for each PC.

Substituting Equation 7.11 into Equation 7.10 yields Var(Y

) =S, demonstrating that the

constraint has been met.

chap-07 4/6/2004 17: 24 page 163

ORDINATION METHODS 163

The next constraint is the requirement that principal component axes have covariances

of zero. This means that the axes must be orthogonal. More formally stated, this constraint

is the requirement that the dot product of any two axes must be zero. For the first two

PCs, the constraint is expressed as:

= 0 =



(7.12)

The general requirement that the products of corresponding coefficients must be zero for

any pair of PCs is expressed as:

= 0(7.13)

The requirements imposed by Equations 7.11 and 7.13 indicate that we are solving for

an orthonormal basis. A basis is the smallest number of vectors necessary to describe a

vector space (a matrix). An orthogonal basis is one in which each vector is orthogonal

to every other, so that a change in the value of one does not necessarily imply a change

in the value of another – in other words, all the variables are independent, or have zero

covariance (Equation 7.13) in an orthogonal basis. An orthonormal basis is an orthogonal

basis in which each axis has the same unit length. This very particular kind of normality

was imposed by the first requirement (Equation 7.11). In an orthonormal basis, a distance

or difference of one unit on one axis is equivalent to a difference of one unit on every other

axis; consecutive steps of one unit on any two axes would describe two sides of a square.

So far, we have defined important relationships among the values of A

. There is an infi-

nite number of possible orthonormal bases that we could construct to describe the original

data. The third constraint imposed above defines the relationship of the new basis vectors

to the original vector space of the data. Specifically, this constraint is the requirement that

the variance of PC1 is maximized, and that the variance of each subsequent component is

maximized within the first two constraints.

We begin with the variance of PC1. From Equation 7.10 we know that:

Var(Y

) = Var





= A

(7.14)

The matrix S can be reduced to:

 =







00... 0

0 λ

0 ... 0

00λ

... 0

000... λ







(7.15)

where each λ

is an eigenvalue, a number that is a solution of the characteristic equation:

S −λ

I = 0(7.16)

chap-07 4/6/2004 17: 24 page 164

164 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

In the characteristic equation, I is the P ×P identity matrix:

I =







100... 0

010... 0

001... 0

000... 1







(7.17)

If each original variable in the data matrix X has a unique variance (cannot be replaced by a

linear combination of the other variables), then each λ

has a unique value greater than zero.

Furthermore, the sum of the eigenvalues is equal to the total variation in the original data.

For each eigenvalue, there is a corresponding vector A

, called an eigenvector, such that:

= λ

(7.18)

This must be true, because we have already required:

S −λ

I = 0(7.19)

Therefore:

(S −λ

I)A

= 0(7.20)

which can be rearranged to:

= λ

(7.21)

Thus, the eigenvectors are a new set of variables with variances equal to their eigenvalues

and covariances equal to zero. Because the covariances are zero, the eigenvectors satisfy the

constraint of orthogonality. Eigenvectors usually do not meet the constraint of normality

=1), but this can be corrected simply by rescaling. Accordingly, the rescaled eigen-

vectors are the PCs, which comprise an orthonormal basis for the variance–covariance

matrix S.

All that remains is to order the eigenvectors so that the eigenvalues are in sequence

from largest to smallest. We can now show that the variance of PC1 is the first and largest

eigenvalue. From Equation 7.10 we have Var(Y

) =A

, and from Equation 7.18 we

have SA

=λ

. Putting these together, we get:

Var(Y

) = A

(7.22)

We can rearrange this to:

Var(Y

) = λ

(7.23)

which simplifies to λ

because we have already imposed the constraint that (A

=1).

A formal proof that principal components are eigenvectors of the

variance–covariance matrix

This is the derivation as presented by Morrison (1990). Let us suppose that we have a

set of measures or coordinates X =(X

, X

...X

), and we want to find the vector

=(A

, A

...A

) such that:

= A

+···+A

(7.24)

chap-07 4/6/2004 17: 24 page 165

ORDINATION METHODS 165

We would like to maximize the variance of Y



i=1



j=1

(7.25)

where s

is the element on the ith row and jth column of the variance–covariance matrix

S of the observed specimens. We can write the variance of Y

in matrix form as:

= A

(7.26)

Now we seek to maximize s

subject to the constraint that A

has a magnitude of one,

which means that (A

=1). To do this, we introduce a term called a Lagrange multiplier

, and use it to form the expression:

+λ



1 −A



(7.27)

which we seek to maximize with respect to A

. Therefore, we take this new expression for

the variance of Y

and set its partial derivative with respect to A

to zero:

∂

∂A



+λ

(1 −A

)



= 0(7.28)

Using Equation 7.26, we can expand the expression for the partial derivative to:

∂

∂A



+λ

(1 −A

)



= 0(7.29)

which we now simplify to:

2(S −λ

I)A

= 0(7.30)

where I is the P ×P identity matrix. Because A

cannot be zero, Equation 7.30 is a vec-

tor multiple of Equation 7.16, the characteristic equation. In Equation 7.30, λ

is the

eigenvalue and A

is the corresponding eigenvector.

Given Equation 7.30, we can also state that:

(S −λ

I)A

= 0(7.31)

This can be rearranged as:

−λ

= 0(7.32)

and simplified to:

−λ

= 0(7.33)

and further rearranged so that:

= λ

(7.34)

This leads to the following substitutions and rearrangements of Equation (7.26):

= A

= λ

(7.35)

Thus, the eigenvalue λ

is the variance of Y

chap-07 4/6/2004 17: 24 page 166

166 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

Interpretation of results

As we stated above, PCA is nothing more than a rotation of the original data; it is simply

a descriptive tool. The utility of PCA lies in the fact that many (if not all) of the features

measured in a study will exhibit covariances because they interact during, and are influ-

enced by, common processes. Below, we use an analysis of jaw shape in a population of

tree squirrels to demonstrate how PCA can be used to reveal relationships among traits.

Fifteen landmarks were digitized on the lower jaws of 31 squirrels (Figure 7.5). These

landmarks capture information about the positions of the cheek teeth (2–5), the incisor

Figure 7.5 Outline drawing of the lower jaw of the fox squirrel, Sciurus niger, showing the locations

of 15 landmarks.

0.0 0.1 0.2 0.3

⫺0.1

⫺0.2

⫺0.3

⫺0.4 ⫺0.3 ⫺0.2 ⫺0.1

0.0

0.1

0.2

Figure 7.6 Plot of landmark coordinates of 31 S. niger jaws after partial Procrustes superimposition.

The locations of landmark 6 in all 31 specimens are enclosed by an ellipse. Similar ellipses could be

drawn for each landmark.

chap-07 4/6/2004 17: 24 page 167

ORDINATION METHODS 167

(1, 14 and 13), muscle attachment areas (6, 9–12, 15) and the articulation surface of the

jaw joint (7 and 8). The 31 specimens include 23 adults and 8 juveniles (individuals lacking

one or more of the adult teeth).

Figure 7.6 shows the landmark configurations of all 31 specimens, after partial Pro-

crustes superimposition. This plot does not tell us much beyond the fact that there is

shape variation in the sample. We can infer from the areas of the scatters for individual

landmarks that there is not much variation in the relative positions of the cheek teeth. In

contrast, many of the ventral landmarks have noticeably larger scatters, suggesting that

their positions relative to the teeth are more variable.

To obtain more precise information about the pattern of shape variation, the 31 sets of

landmark coordinates are converted into shape variables (see Chapter 6 for review), and

these shape variables are subjected to PCA. The 15 landmarks yield 26 shape variables,

so there are 26 PCs, and 26 scores for each specimen (its score on each component). The

output from PCA consists of the list of coefficients describing the PCs, the variance of each

component and its percentage of the total variance, and the scores of each specimen on

each component.

As shown in Table 7.1, each PC has progressively less variance. Many of the components

represent such a small proportion of the total variance that it is reasonable to ask whether

Table 7.1 Eigenvalues from PCA of squirrel jaws

PC Eigenvalues % of total variance

1 1.13 ×10

−3

51.56

2 2.15 ×10

−4

9.83

3 1.64 ×10

−4

7.49

4 1.36 ×10

−4

6.22

5 1.16 ×10

−4

5.32

6 9.52 ×10

−5

4.36

7 7.18 ×10

−5

3.28

8 5.45 ×10

−5

2.49

9 4.49 ×10

−5

2.05

10 3.58 ×10

−5

1.64

11 3.25 ×10

−5

1.49

12 2.36 ×10

−5

1.08

13 1.79 ×10

−5

0.82

14 1.37 ×10

−5

0.63

15 9.83 ×10

−6

0.45

16 9.31 ×10

−6

0.43

17 6.87 ×10

−6

0.31

18 3.72 ×10

−6

0.17

19 3.06 ×10

−6

0.14

20 2.17 ×10

−6

0.10

21 1.66 ×10

−6

0.08

22 7.04 ×10

−7

0.03

23 5.37 ×10

−7

0.02

24 3.62 ×10

−7

0.02

25 1.15 ×10

−7

0.01

26 5.02 ×10

−8

<0.01