Zelditch M.L. (и др.) Geometric Morphometrics for Biologists: a primer

Подождите немного. Документ загружается.

chap-05 4/6/2004 17: 23 page 128

128 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

clicking on Show Procr (PA). This will rotate the reference shape so that its principal axis

is aligned with the Y-axis. If none of these provide a reasonable orientation, don’t panic;

other IMP programs have interactive tools that allow you to rotate pictures of results

(shape differences) through any desired angle.

References

Bookstein, F. L. (1996). Combining the tools of geometric morphometrics. In Advances in

Morphometrics (L. F. Marcus, M. Corti, A. Loy et al., eds) pp. 131–151. Plenum Press.

Chapman, R. E. (1990). Conventional Procrustes methods. In Proceedings of the Michigan Mor-

phometrics Workshop (F. J. Rohlf and F. L. Bookstein, eds) pp. 251–267. University of Michigan

Museum of Zoology.

Dryden, I. L. and Mardia, K. V. (1998). Statistical Shape Analysis. John Wiley & Sons.

Dryden, I. L. and Walker, G. (1999). Highly resistant regression and object matching. Biometrics,

55, 820–825.

Kim, K., Sheets, H. D., Haney, R. A. and Mitchell, C. E. (2002). Morphometric analysis of ontogeny

and allometry of the Middle Ordovician trilobite, Triarthrus becki. Paleobiology, 28, 364–377.

Liebner, D. L. and Sheets, H. D. (2001) Superposer, available on the IMP website www.canisius,

edu/∼sheets/morphsoft.html

Press, W. H., Flannery, B. P., Teukolsky, S. A. and Vetterling, W. T. (1988). Numerical Recipes in

C: The Art of Scientific Computing. Cambridge University Press.

Rohlf, F. J. (1990). Rotational fit (Procrustes) methods. In Proceedings of the Michigan Morpho-

metrics Workshop (F. J. Rohlf and F. L. Bookstein, eds) pp. 227–236. University of Michigan

Museum of Zoology.

Siegel, A. F. and Benson, R. H. (1982). A robust comparison of biological shapes. Biometrics, 38,

341–350.

Walker, J. A. (2000). Ability of geometric morphometric methods to estimate a known covariance

matrix. Systematic Biology, 49, 686–696.

Webster, M., Sheets, H. D. and Hughes, N. C. (2001). Allometric patterning in trilobite

ontogeny: testing for heterochrony in Nephrolenellus.InBeyond Heterochrony: The Evolution

of Development (M. L. Zelditch, ed.) pp. 105–144. Wiley-Liss.

Zelditch, M. L., Lundrigan, B. L., Sheets, H. D. and Garland, T. Jr (2003). Do precocial mammals

develop at a faster rate? A comparison of rates of skull development in Sigmodon fulviventer and

Mus musculus domesticus. Journal of Evolutionary Biology, 16, 708–720.

chap-06 4/6/2004 17: 23 page 129

The thin-plate spline: visualizing shape

change as a deformation

Shape coordinates of all kinds are fundamentally limited when it comes to depicting trans-

formations in shape – they cannot tell us what happens between landmarks. Sometimes it

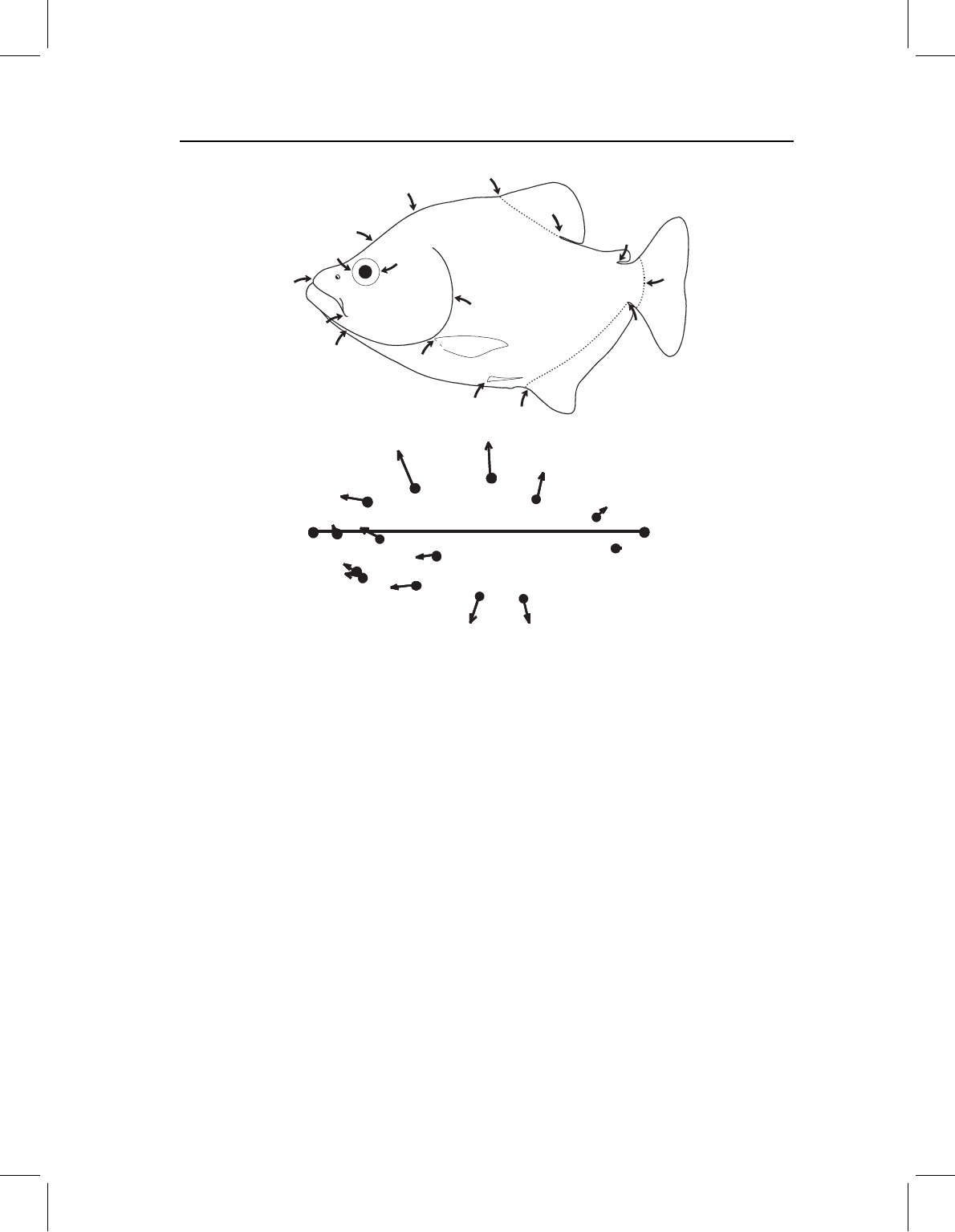
is obvious what happens between landmarks, as in Figure 6.1, where we can see that the

snout elongates relative to the eye. That is obvious because the posterior eye landmark is

displaced towards the anterior eye landmark, and that anterior eye landmark is not dis-

placed towards the snout – so the snout must be lengthening relative to the eye. However,

it is not so obvious whether the postorbital region is elongating (relative either to the head

or body). Similarly, it is difficult to judge whether the head (as a whole) elongates relative

to the postcranial body. The problem is not that we lack landmarks in the relevant regions;

rather, it is that so many landmarks are displaced relative to the others that it is mentally

exhausting to track what happens between them all. That tracking requires looking at the

lengths of all the vectors to determine whether several landmarks are displaced to a sim-

ilar degree in concert, or if some are displaced relatively more than others (thereby either

increasing or decreasing the distance between them). Even the landmarks that are not dis-

placed relative to others must be considered. What we need is a method for visualizing

changes between landmarks over the entire form.

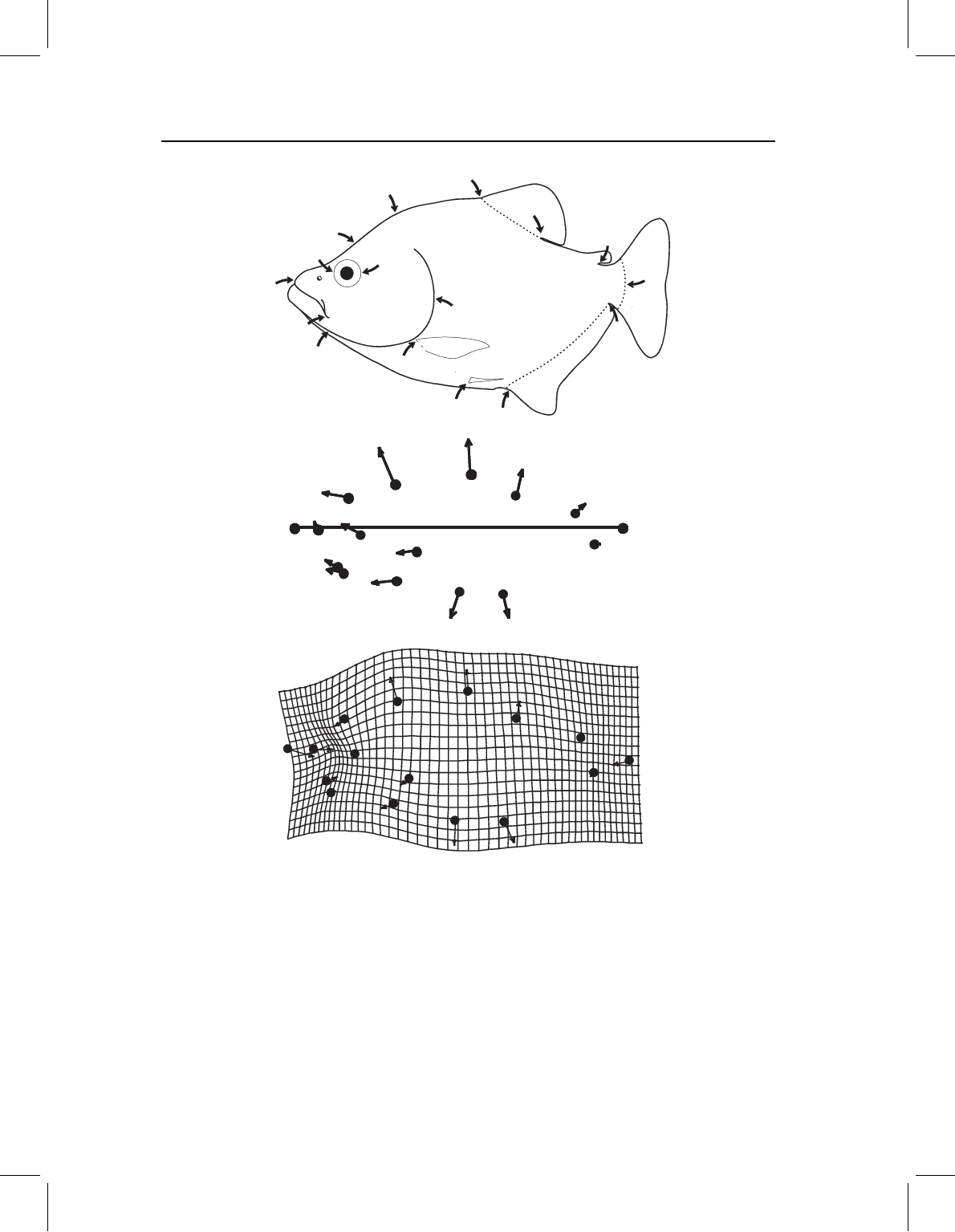
That visualization is the primary purpose of the thin-plate spline. Using it, we can

interpolate between landmarks, taking all displacements of all landmarks relative to all

others into account (Figure 6.2). The other major purpose of the spline has been men-

tioned previously in this text: we need a set of shape variables to use in conventional

statistical tests. Specifically, we need a set of variables that spans the entire space of our

data but numbering only 2K −4 for two-dimensional data (more generally, numbering

(KM −1 −M −(M(M −1)/2)) where K is the number of landmarks in M dimensions).

The spline provides such a set. Unlike the coordinates obtained by the Procrustes-based

superimposition methods, the thin-plate spline coefficients (called partial warp scores) can

be used in conventional statistical tests without adjusting the degrees of freedom. Also

unlike the coordinates produced by the two-point registration, which also have the appro-

priate number for statistical tests, the partial warp scores employ the correct tangent space

ISBN 0–12–77846–08 All rights of reproduction in any form reserved

chap-06 4/6/2004 17: 23 page 130

130 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

Figure 6.1 Ontogenetic change in body shape of Serrasalmus gouldingi, depicted by relative

displacements of Bookstein shape coordinates.

measure of distance – the Procrustes distance. Using partial warps you will get precisely

the same results as you get using the coordinates obtained by the Procrustes (GLS) super-

imposition if you correctly adjust the degrees of freedom, or use tests that calculate them

properly (like Goodall’s F).

In summary, the thin-plate spline provides a visually interpretable description of a defor-

mation, with the same number of variables as there are statistical degrees of freedom, and

it employs the Procrustes distance as a metric. Even if we were not concerned with the

advantages of the spline for graphical analysis, we might still want to use it for purposes of

statistical inference. Conversely, even if we were not concerned with the advantages of the

spline for statistical analysis, we might still wish to use it for its graphical capabilities. You

can use the spline to depict your results, and you can use partial warps in your statistical

analyses without worrying that the mathematical details (and complexities) will have any

impact on your results. The spline is a convenient tool for visual display and for obtaining

variables with the correct degrees of freedom – it is nothing more (or less) than that.

In this chapter, we begin with a basic overview of the mathematical idea of a defor-

mation. We then discuss the mathematical metaphor underlying one particular model of

a deformation, the thin-plate spline, and how we can decompose it to yield variables.

In general, we present a largely intuitive overview before delving more deeply into the

mathematics.

chap-06 4/6/2004 17: 23 page 131

THE THIN-PLATE SPLINE 131

Figure 6.2 Ontogenetic change in body shape of S. gouldingi, depicted both by relative displace-

ments of Bookstein shape coordinates and by the thin-plate spline.

Modeling shape change as a deformation

A deformation is a smooth function that maps points in one form to corresponding points

in another form. Intuitively, smoothness means that the function goes on without inter-

ruptions or abrupt changes. More precisely, it means that the function is continuously

differentiable (it can be differentiated, its first derivative can be differentiated, and so can

its second, and so forth). To be differentiable, a function must be continuous. For example,

the function Y =X

is continuous, but the absolute value function is not because it has a

chap-06 4/6/2004 17: 23 page 132

132 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

sharp corner at X =0 and so is not differentiable at that point. The Dirichelet function

Y ={1 when X is rational; 0 when X is irrational} is also not continuous – it is not dif-

ferentiable anywhere. To be continuous, it is not enough to have a first derivative, that

first derivative must also be a differentiable function. That deformations are continuously

differentiable is important, because it means that the function must extend between land-

marks – it cannot be defined only at certain discrete points and disappear in the regions

between them.

If a function blows up (becomes infinite or non-differentiable) between points, we cannot

use it to interpolate values between them. This is important because we are using the thin-

plate spline as an interpolation function, inferring what happens between landmarks from

data at given anatomical points. If it is unreasonable to interpolate, it is unreasonable to

use the thin-plate spline for that purpose. It is also unreasonable to interpolate between far

distant landmarks, just as it is unreasonable to extrapolate a linear regression far beyond

the range of the observed data. If our landmarks are far apart, we have too few data

to draw conclusions about what happens between them. For example, in Figure 6.2 we

are assuming that the changes in regions between postcranial landmarks can be inferred

from landmarks on the dorsal and ventral periphery. That assumption can be questioned,

because if we actually had more landmarks in that region we might find abrupt changes –

small regions where the grid dramatically compresses or expands. We are simply assuming

that no such localized changes occur.

Another case in which it would be inappropriate to think of shape change as a defor-

mation is when there is change concentrated at a single landmark. That is equivalent to a

function with an abrupt change, which violates the assumption of continuity. Such discon-

tinuities can be detected as displacement of one shape coordinate against a background

of invariant points. That pattern may be rare, but one close to it has actually been found

in data (Myers et al., 1996). In that study, mice (Peromyscus maniculatus bairdii) fed

different diets were found to have skulls that differ only in the location of the tips of the

incisors relative to the other skull landmarks. This is an extreme case of a Pinocchio effect

(as discussed in Chapter 5). Such highly local changes should be ruled out before any

deformation-based method is applied; if such highly localized change is found, it is better

to rely on shape coordinates.

There is one other case in which a deformation-based approach might be unwise; when

the interpolation spans a large amount of extra-organismal space – that is, when it is

interpolating the changes over regions of “tissue” outside the organism. This can happen

when landmarks are located at tips of long structures, or on structures that extend far

laterally. Normally this is not a serious problem because we can simply avoid interpreting

the changes in regions between those landmarks, except to say (perhaps) that the long

bony structures are relatively elongated or reoriented more laterally. However, this can

be a problem when multiple landmarks are located at tips of long structures and no other

landmarks serve to pin down what is happening to the regions between them. It is possible

to analyze the changes in relative position and length of those tips using shape coordinates,

but it may not be wise to draw a grid interpolating changes at those tips to regions between

them – there is no organismal tissue there.

If we do not have one of the special cases described above – that is, if we do not

have evidence that some landmarks are largely independent of the others – then we can

apply an interpolation function to understand changes between landmarks. Because the

chap-06 4/6/2004 17: 23 page 133

THE THIN-PLATE SPLINE 133

interpolation function is continuously differentiable, relative displacements of landmarks

can be used to calculate the displacement of any location on the organism. These inferred

displacements between landmarks can be illustrated using a variety of graphical styles;

Figure 6.2 demonstrates the one most often used, a deformed grid in the style of D’Arcy

Thompson (1942).

The physical metaphor

The mathematical basis for drawing the picture of the deformed grid is a metaphor –

the bending of an idealized steel plate (Bookstein, 1989). According to this metaphor,

displacements of landmarks in the X, Y plane (the plane in which we have drawn them

in Figure 6.1) are visualized as if they were transferred to the Z-coordinate of an infinite,

uniform and infinitely thin steel plate. That is, instead of depicting a landmark as displaced

in some direction within the plane of this page, it is visualized as if it were displaced in the

third dimension (out of this page).

The metal plate is constrained by little stalks that weld the landmarks in one shape

to the landmarks in the other. This is difficult to draw because the imagery is inherently

three-dimensional, so imagine two plates and place a configuration of landmarks on each.

Now, put one plate above the other, and construct little stalks that attach a landmark

on one plate to its homologue on the other plate. If a landmark in one shape is displaced

a long distance relative to the other landmarks, construct a long stalk. Thus when the

landmark is displaced a long distance in one direction (such as far anteriorly) the stalk

is long; conversely, when displaced only a short distance the stalk is short. Therefore the

stalks are of uneven lengths, and that unevenness means that one plate cannot be flat. The

conformation that plate takes is determined by the relative heights of the stalks, and by

the distances between them on the plate.

In some cases the plate simply tilts or rotates (it does not actually bend); in other cases

the plate must actually bend, such as when a point in the middle is elevated higher than

four surrounding points. That bending may be gentle or quite sharp. For real steel plates,

the conformation of the plate tends to minimize the magnitude of bending over the whole

plate (as well as the physical energy required to produce that bending). Here we use the

expression tends to minimize the magnitude and energy of bending, because real steel

plates may have flaws, and the situation is not a pure case of work against elasticity. In

the ideal case, the bending energy depends solely on the distance between the points and

the relative heights of the stalks, and the total amplitude of bending. If we consider two

different deformed plates, both describing the same total overall amount of change (the

same set of stalk heights) but one with the stalks proportionately closer together, the one

that is bent between the more closely spaced points requires more energy than the one that

is bent between more widely spaced points.

The bending energy depends on the spacing of the stalks because it is a function of the

rate of change in the slope of the plate – i.e. whether the slope of the surface increases

rapidly or slowly. In these terms, more energy is required when the slope of the surface

changes at a higher rate (for the same net amplitude of change). Imagine a tall stalk sur-

rounded by short ones, which induces a steep slope in the curvature of the plate. The

steepness of that slope is proportional to the function being minimized – the rate of change

chap-06 4/6/2004 17: 23 page 134

134 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

in slope of the surface – and thus the function being minimized is a function of the second

derivative (the slope of the surface is the first derivative) integrated over the whole surface

of the plate. It can also be termed the integral of the quadratic variation over the plate.

To return from ideal plates to the analysis of a deformation, we now project the changes

that were visualized as if in the Z-direction back into the X, Y plane (the plane of our

landmark data). The idea of bending that had a physical meaning when we were talking

about changes in the Z-direction is now reinterpreted as “spatially local information.”

This interpretation may not be intuitively obvious, but consider what a relatively rapid

increase in slope means – that there are contrasting displacements of closely spaced points.

When closely spaced points change in opposite directions it requires more energy to bend

the plate between them; so there is an inverse relationship between the spatial scale of the

change and its metaphorical bending energy. Minimization of bending energy is equivalent

to minimization of spatially localized information.

It is always possible to envision changes as highly local by assuming that the plate

flattens out immediately after rising, then rises again just at the next stalk, then flattens

again, then rises again, etc. The argument against doing so is that this would be the most

unparsimonious interpretation possible. By minimizing bending energy, we obtain a more

parsimonious description of the change. We do not assume highly localized change unless

the data demand doing so.

Uniform and non-uniform components of a deformation

Some transformations require no bending energy at all; these are equivalent to tilting

or rotating the plate. These are often called affine or uniform transformations, meaning

that they leave parallel lines parallel. The terms “affine” and “uniform” are both used to

describe the same component of a deformation; “affine” is favored by mathematicians, but

“uniform” appears more often in the geometric morphometric literature. Consequently,

we will use “uniform” for this component and “non-uniform” for its complement. In our

example (Figure 6.2), if the entire fish simply elongates relative to its depth, without any

disproportionate lengthening of one region relative to another, that is a uniform elongation.

Uniform elongation is equivalent to uniform narrowing, as should be recalled from our

discussion of shape variables in previous chapters. Because it is uniform, meaning that

the same change occurs everywhere, we need only one descriptor for the change of the

whole organism. In contrast, the non-uniform or non-affine deformations (which involve

the metaphorical bending) have regionally differentiated effects.

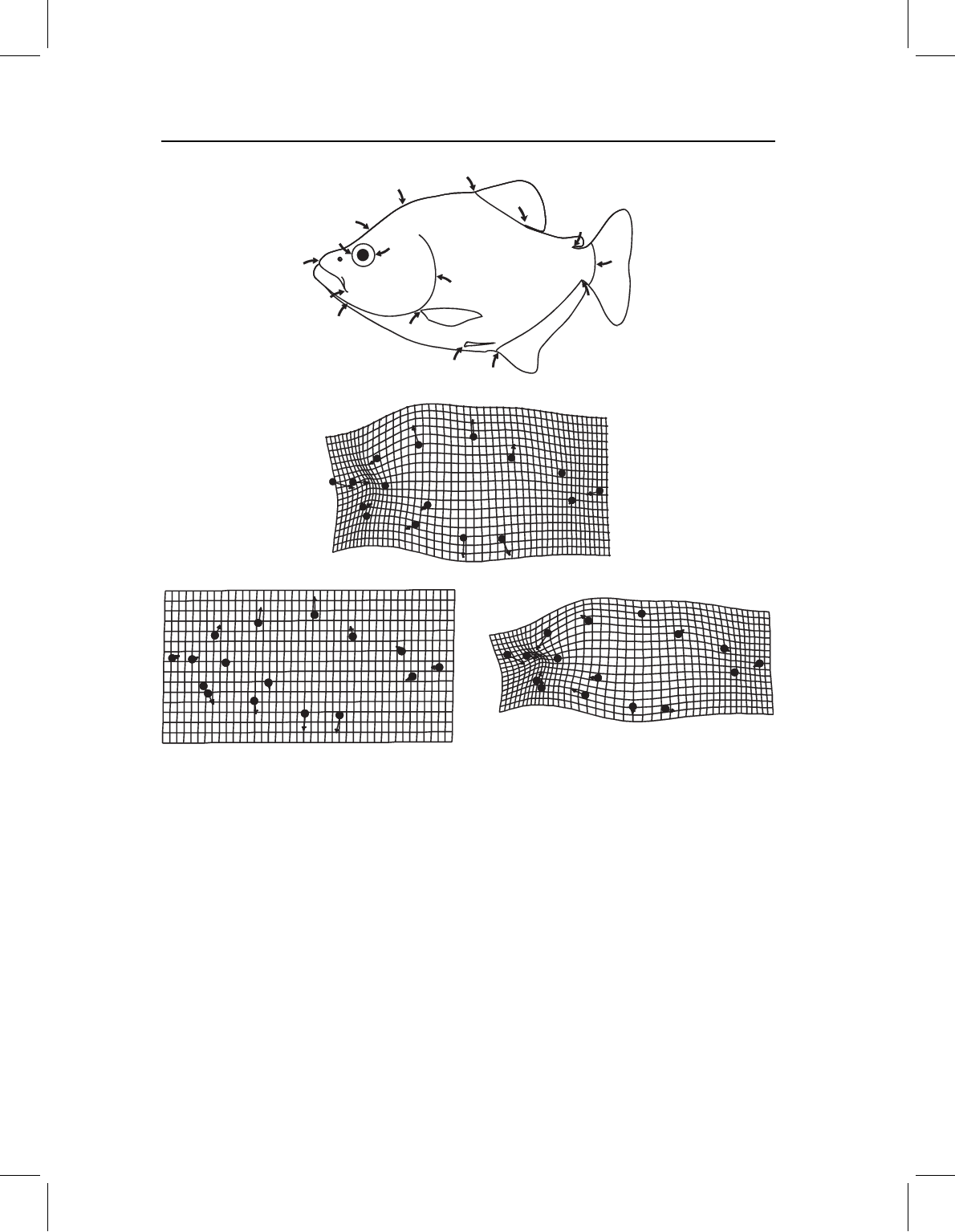
A deformation can be broken down into uniform and non-uniform components, as in

Figure 6.3. Most real biological transformations will have both uniform and non-uniform

components. These components are computed separately, so we describe them separately

(first the uniform, then the non-uniform), but it is important to bear in mind that a complete

description, and an accurate illustration, requires specifying all the components.

Uniform (affine) components

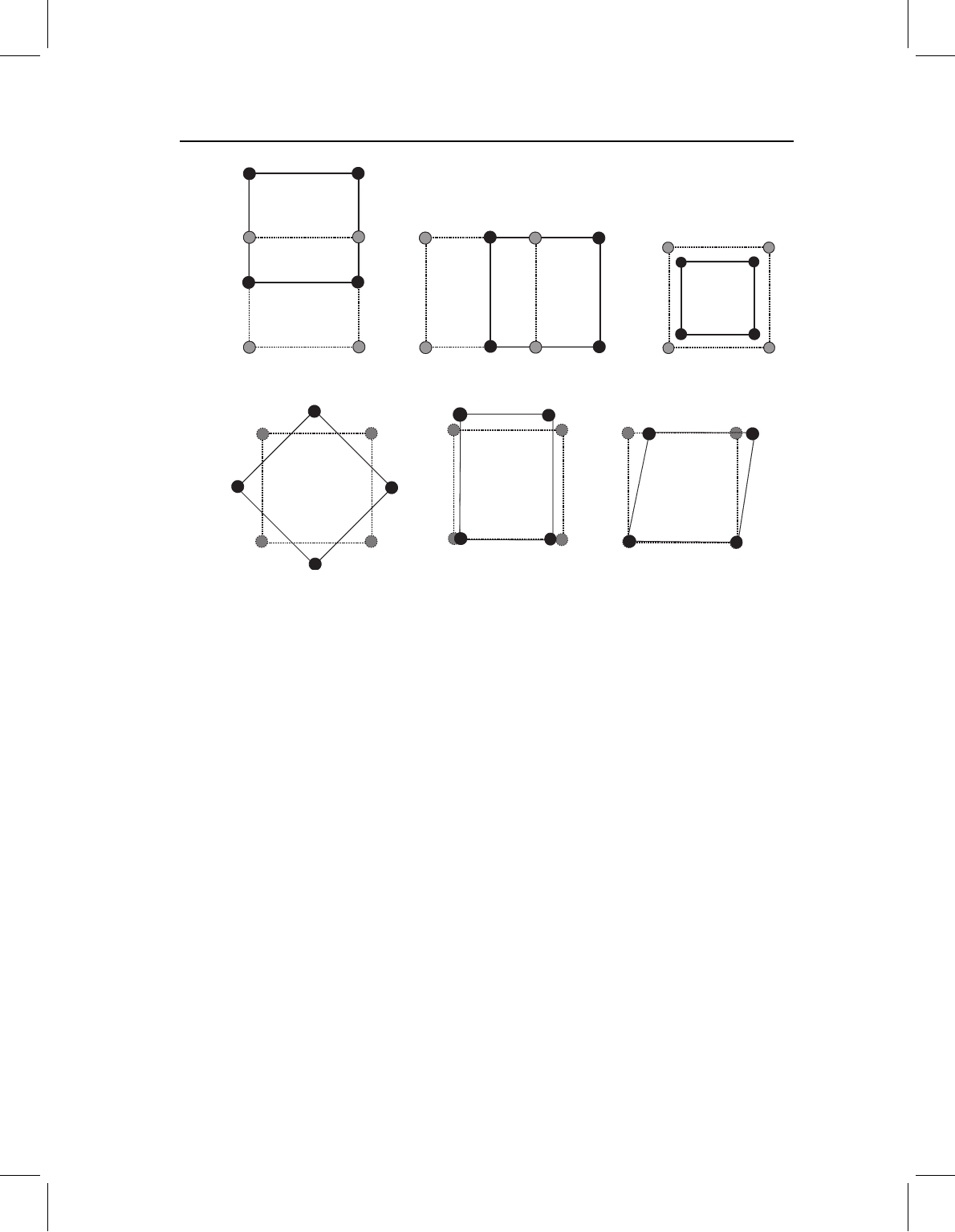
There are six distinct types of uniform deformations for landmarks in two dimensions, and

they are independent of each other (meaning that they are mutually orthogonal). Figure

6.4 shows these six operations carried out on a square configuration of landmarks. The

chap-06 4/6/2004 17: 23 page 135

THE THIN-PLATE SPLINE 135

(A)

(

)(

)

Figure 6.3 Ontogenetic change in body shape of S. gouldingi, depicting: (A) the total deformation

and its two components; (B) uniform component; (C) non-uniform component.

first four are the familiar ones that do not alter shape: translation along two perpendicular

axes (Figures 6.4A, 6.4B), scaling (Figure 6.4C) and rotation (Figure 6.4D). These are

all used in superimposing shapes. The other two uniform deformations do alter shape:

compression/dilation (Figure 6.4E) and shear (Figure 6.4F). Compression/dilation refers

to the case in which one direction has expanded (the vertical or Y-direction in Figure

6.4E) while the other has contracted (the horizontal or X-direction). Shearing refers to

translating landmarks along one axis by a distance proportional to their location along

the other axis.

Because compression/dilation and shear alter shape whereas translation, rotation and

scaling do not, it is common to talk about the two that alter shape without mentioning the

ones that do not. All of them need to be tracked, so we will refer to compression/dilation

chap-06 4/6/2004 17: 23 page 136

136 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

(A) (B) (C)

(D) (E) (F)

Figure 6.4 The six uniform (affine) transformations: (A) translation along the vertical axis; (B)

translation along the horizontal axis; (C) scaling; (D) rotation; (E) compression/dilation; (F) shearing.

The original (or reference) square is shown with dotted lines, while the deformed shape is shown

with solid lines.

and shear as the explicit uniform deformations or explicit uniform terms because they are

the ones explicitly tracked. We will refer to the others as the implicit uniform deformations

or implicit uniform terms. They are implicit because they can be mathematically determined

from the superimposition method used, the explicit uniform components, and the non-

uniform components of a deformation – they are the translation, rotation and scaling

that must have been carried out. Both explicit and implicit uniform terms are needed, in

addition to the non-uniform terms, to draw the deformation correctly.

Each deformation has an inverse. Applying the inverse of a deformation is equivalent to

traveling backwards along the path that was taken until we arrive back at the starting point.

We can think of the deformation in terms of a 2K-dimensional vector (i.e. two dimensions

per landmark). There would be a vector at each landmark indicating the direction in

which that particular landmark will be mapped under the deformation (although there

are only 2K −4 independent dimensions). In the inverse of the deformation, the directions

of the arrows would be reversed. The inverse of a translation is the same magnitude of

translation in the opposite direction (negative X instead of positive X). Similarly, we

can represent rotation as an angular displacement so its inverse is a negative angular

displacement (counterclockwise instead of clockwise). Scaling is slightly different because

it involves multiplication (whereas translations and rotations could be treated as additions).

Scaling is multiplication by a factor F; its inverse is multiplication by the inverse of F(1/F).

chap-06 4/6/2004 17: 23 page 137

THE THIN-PLATE SPLINE 137

Unfortunately, the algebraic descriptions of the last two deformations and their inverses

are not quite as simple (as we will see below). Graphically, we can see that the inverse of

compression/dilation involves a reversal of which axis is compressed and which is dilated,

and that the inverse of a shear is a shear of the same amount along the same axis in the

opposite direction.

Calculating the shear and compression/dilation terms

Here we present the mathematical derivation of formulae for calculating the uniform com-

ponents of a deformation that changes shape. Unlike the formulae for computing the

non-uniform part of a shape change, which have been stable over the last decade, the for-

mulae for computing the uniform part have changed repeatedly. Over the last several years,

the uniform component has been computed using the formulae presented by Bookstein

(1996). These, which are based on the Procrustes distance, are the ones we present here.

We begin with a conceptual framework for Bookstein’s derivation of the current formulae;

then follow that with the full mathematical details.

Conceptual framework The goal of this derivation is to find a unit vector that describes

the direction of deformation at each landmark due to shearing or compression/dilation,

followed by a Procrustes generalized least squares (GLS) superimposition of the deformed

shape back onto the original (undeformed) one. This represents what we measure in data:

a deformation followed by a superimposition operation. Thus, both mappings must be

taken into account. When we are done, we will have a set of unit vectors that describe

the deformation under shearing or under compression/dilation. We can then take the dot

product of the observed deformation with the unit vectors to obtain the component of

the observed deformation lying along the shear or compression/dilation vectors. These are

what we have been calling the explicit uniform components of the deformation.

Notice that we are taking a verbal description of the situation, turning the verbal

statement into two mathematical operations or mappings (shear or compression/dilation,

followed by the superimposition), then using those mappings to determine the direction

of the vectors describing the deformation. That allows us to calculate components of any

deformation along those desired directions. What might not be obvious yet is that vec-

tors describing the uniform deformations depend on only one form – the one that we are

modeling as deformed, which we will call the reference form (the other is the target). This

terminology should be familiar – the reference form is the same one that we discussed in

Chapter 4. If you do not wish to read further, you do not have to. You can go directly to

the section on decomposing the non-uniform (non-affine) component.

Although we now have a general idea of the procedure, there are still a few ideas that

need to be added. The first is the idea of complex number notation for landmark locations,

which is often used in mathematical derivations (see Dryden and Mardia, 1998, for exam-

ple). Consider a landmark configuration consisting of K landmarks in two dimensions,

which we will call Z, the reference form. Mathematically, we will say:

Z =



, Z



, Y



j=1

(6.1)

which means that Z is a set of K pairs of landmark positions Z

,or(X

, Y

). It is a useful

mathematical shortcut to think of Z

as being a complex number Z

+iY

, where