Zelditch M.L. (и др.) Geometric Morphometrics for Biologists: a primer

Подождите немного. Документ загружается.

chap-05 4/6/2004 17: 23 page 108

108 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

(B)

(A)

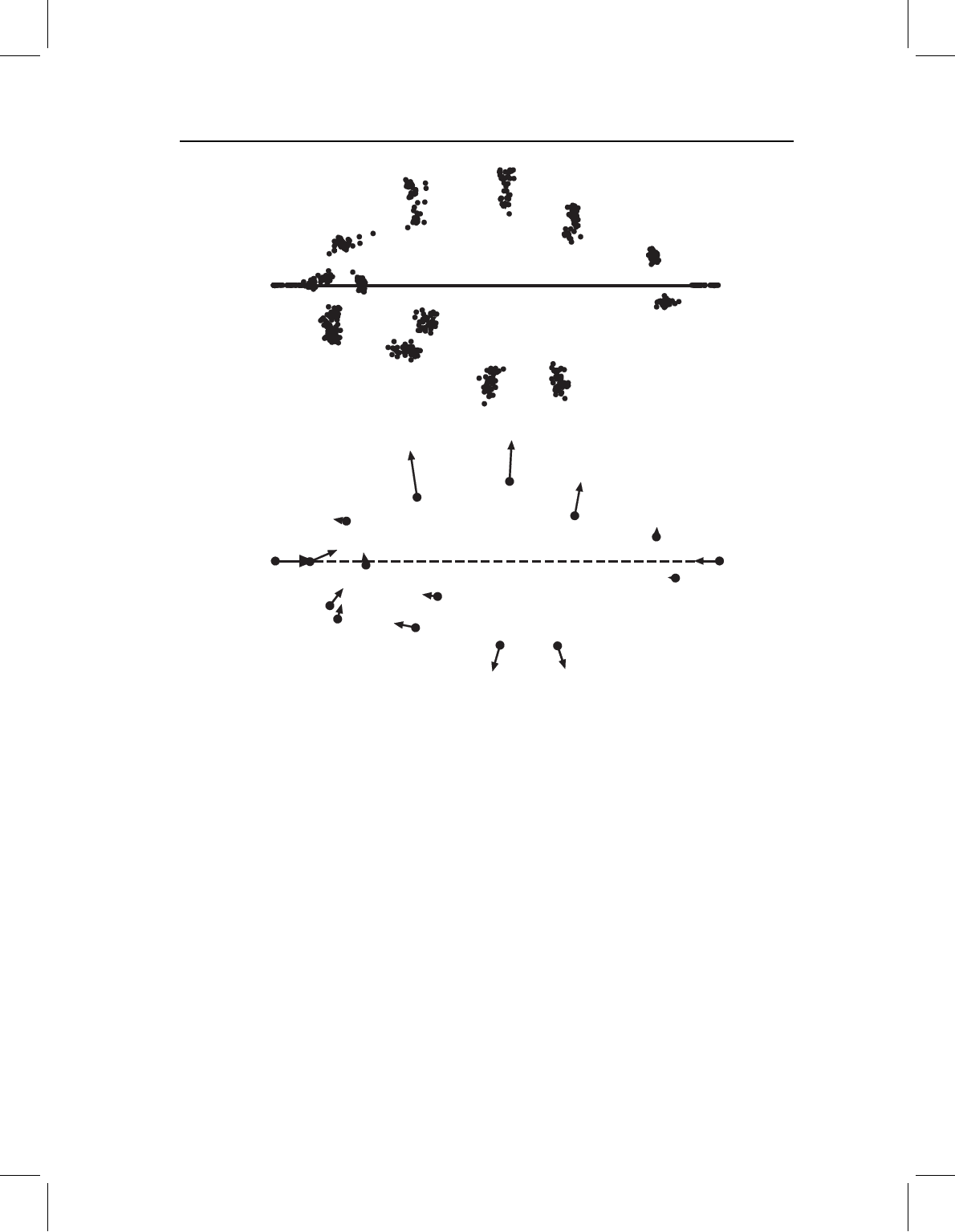
Figure 5.3 Ontogenetic variation in S. gouldingi visualized relative to a baseline on the dorsal head

(landmarks 2 and 3): (A) coordinates of landmarks relative to the baseline; (B) vectors indicating

displacements of landmarks relative to the fixed baseline. (Note the apparent rotation of landmarks

around this baseline.)

landmarks (because they covary to a high degree), and is expressed as displacement of every

other landmark away from the dorsal edge. In addition, the elongation of the middle of

the body relative to the rest of the piranha is now expressed as a relative contraction of

the ends towards the middle.

If we use a baseline that rotates relative to most of the other landmarks, the resulting

superimposition seems to indicate that the piranha’s body rotates around the baseline as

it grows (Figure 5.3).

Clearly the baselines used in Figures 5.2 and 5.3 are spectacularly bad choices; how-

ever, they simply exaggerate the general problem that the variance of baseline points is

transferred to the other landmarks. It should be intuitively obvious, even if not visibly

so, that the actual anatomical landmarks are really no more variable than in Figure 5.1;

changing the baseline does nothing to the data set but rotate and rescale it. The conse-

quences for our perception of the shape differences can be dramatic, particularly when it

makes the data seem inordinately noisy, but they can be understood as the consequences

of a change in perspective. What makes this transfer of variance really worrisome is that

it is not necessarily unbiased – it is related to the distance of the free landmarks to the

baseline (Dryden and Mardia, 1998). Consequently, the transfer of variance can induce

chap-05 4/6/2004 17: 23 page 109

SUPERIMPOSITION METHODS 109

correlations among landmarks (compare the relative displacement of the most posterior

landmarks across the three baseline registrations).

A second disadvantage arising from standardizing the coordinates of the baseline points

is that this superimposition does not minimize the distance between configurations (the

summed squared distance between corresponding landmarks). Scaling configurations of

landmarks to unit baseline length need not produce configurations of the same centroid

size, much less configurations of unit centroid size. Similarly, the rotation to align the base-

line is unlikely to be the exact rotation needed to remove rotational effects, as prescribed

by Kendall. Consequently, the summed squared distances between corresponding land-

marks is not the minimized partial Procrustes distance between shapes. In other words,

the configurations produced by the two-point registration do not differ solely in shape (as

defined by Kendall), so the graphics based on this superimposition cannot be said truly to

embody the differences between shapes. This is not merely a graphical problem; it is also a

serious metrical problem. There is a profound conceptual and mathematical inconsistency

between the distances measured as summed squared differences of shape coordinates, and

the Procrustes distances between shapes in shape space. This discrepancy is likely to be

especially large when the baseline points are close together and more variable than most

other landmarks (as in Figures 5.2 and 5.3), but no choice of baseline can completely

eliminate the problem.

Given these rather substantial disadvantages, it is useful to have alternative superim-

position methods. The first alternative we discuss is conceptually similar to the two-point

registration, but addresses the problems of scaling and variance transfer. The second alter-

native addresses the discrepancy between distance metrics. The third alternative is concep-

tually related to the second, but addresses problems arising from highly localized shape

change.

Sliding baseline registration

The sliding baseline registration (SBR) was developed by David Sheets in collaboration

with Mark Webster (Webster et al., 2001) and Keonho Kim (Kim et al., 2002) to reduce

the disadvantages of aligning landmark configurations along one edge as in the two-point

registration. To that end, configurations are scaled to unit centroid size, which directly

addresses the conceptual and mathematical inconsistency between the scaling used in the

superimposition and the scaling used in the definition of shape. As we will demonstrate

below, this also reduces the problem of variance transfer. Because the configurations are

scaled to unit centroid size, their baselines will usually differ in length and consequently,

the two end points cannot be superimposed simultaneously. Instead, their Y-coordinates

are fixed at zero and their X-coordinates are allowed to vary as necessary to align the

X-coordinates of the centroids at the zero, in effect sliding the baseline along the X-axis.

(The Y-coordinate of the centroid is the average perpendicular distance of the landmarks

from the baseline after scaling to unit centroid size.)

At first glance, the SBR superimposition appears to indicate that the S. gouldingi

ontogeny involves a smaller increase in body depth than was seen using BC (Figure 5.4).

Closer examination reveals that the baseline is getting shorter as depth increases, so

the increase in relative depth is the same (scaling to the same size makes adults, with

chap-05 4/6/2004 17: 23 page 110

110 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

(B)

(A)

Figure 5.4 Ontogenetic variation in S. gouldingi visualized by sliding baseline registration. As

in Figure 5.1, the baseline is formed by the two most distant landmarks, 1 and 7. (A) Coordinates

of landmarks relative to the baseline; (B) vectors indicating displacements of landmarks relative

to the fixed baseline. (Note the lesser apparent magnitude of the variance landmarks compared to

Figure 5.1.)

relatively deeper bodies, look both shorter and deeper). This difference arises because

part of the variation in the relative positions of the baseline endpoints is expressed in the

X-coordinates of those points under the SBR superimposition. This also means that SBR

transfers correspondingly less variance to the other landmarks.

Although SBR can reduce the variance that is transferred to the free landmarks, it

cannot completely eliminate the problem. The tremendous deepening of the midbody of

S. gouldingi still induces a large covariance among the other landmarks if the dorsal land-

marks are used for the baseline (Figure 5.5).

When the baseline also rotates relative to the other landmarks, that rotation can be a

more prominent component of the induced covariance under SBR than in BC (Figure 5.6).

Therefore, SBR cannot compensate for a poor choice of baseline.

Another problem that SBR shares with BC is that the implied displacements of the

landmarks still do not equal the partial Procrustes distance between the shapes. Again,

the configurations are not centered on the centroid (although they are closer after SBR),

chap-05 4/6/2004 17: 23 page 111

SUPERIMPOSITION METHODS 111

(A)

(B)

Figure 5.5 Ontogenetic variation in S. gouldingi visualized by sliding baseline registration, using a

baseline near the dorsal edge of the body (landmarks 3 and 5): (A) coordinates of landmarks relative

to the baseline; (B) vectors indicating displacements of landmarks relative to the baseline. Less vari-

ance is transferred than was the case when this baseline was fixed, but there are still substantial

induced correlations because the variance of the baseline endpoints is mostly perpendicular to the

baseline.

nor are they rotated to the orientations that minimize the summed squared distances

between the corresponding landmarks. This means that the configurations produced by

SBR, like those produced by BC, do not differ solely in shape as defined by Kendall; they

are not the same set of configurations as would appear in Kendall’s shape space. Even so,

the configurations produced by SBR might be preferable if the orientation of the baseline

has some biological significance. In that case, we might judge that rotation does change

shape, so the only rotation permitted during superimposition is that which corrects an

earlier misalignment when specimens were digitized. By choosing to rotate each configu-

ration to a specific orientation, we have effectively chosen to include information about

orientation (i.e. “rotational effects”) in what we mean by “information about shape.”

This is not a trivial choice; it takes us away from the mathematical theory discussed in

Chapter 4.

chap-05 4/6/2004 17: 23 page 112

112 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

(A)

(B)

Figure 5.6 Ontogenetic variation in S. gouldingi visualized by sliding baseline registration, using

a baseline (landmarks 2 and 3) that rotates relative to most other landmarks: (A) coordinates of

landmarks relative to the baseline; (B) vectors indicating displacements of landmarks relative to the

baseline. Again, there is improvement relative to fixing the length of this baseline, but substantial

induced correlations remain.

In addition to the lingering problems shared with BC (variance transfer and constrained

alignment), SBR has a new problem that may also limit its utility for data analysis. By

allowing the X-coordinates of the two baseline points to vary, two new variables are added

to the analysis. Consequently, the number of variables exceeds the number of degrees of

freedom by two. Thus, if these coordinates are to be analyzed using conventional statistical

methods, such as Hotelling’s T

, we must exclude two coordinates from the analysis.

Unfortunately there is no general rule for deciding which to exclude, and there is an

obvious risk that the ones selected are chosen because they produce the desired results.

chap-05 4/6/2004 17: 23 page 113

SUPERIMPOSITION METHODS 113

One possible solution is to try all possible pairwise combinations of dropped coefficients,

asking if the statistical results are robust to the choice. A better solution is to replace the

conventional statistical methods with resampling-based methods, which do not require

estimates of the degrees of freedom (see Chapter 8).

Even if you decide that SBR (or BC) is not appropriate for analysis, you can still choose

to use it for purely graphical purposes, reserving the statistical analysis for the coordinates

introduced in the next section. This will not lead to any inconsistencies between statistical

and biological inferences; the statistical inferences should not depend on the choice of

variables, and nor should any biological inferences. Obviously the statistical tests must be

based on some set of variables, and so must the pictures, but if the analyses and the pictures

are done correctly, all complete sets of variables will yield the same statistical results and

all illustrations of those results will support the same interpretations.

Generalized least squares Procrustes superimposition

Of all the topics covered in this book, this section on the generalized least squares Procrustes

superimposition (GLS) may be the most important. For reasons discussed below, this is

the generally favored superimposition method. This is the method we (and many others)

use to take the raw data from the digitizer and turn it into the data we analyze. If you

understand the coordinates obtained by GLS, you understand enough about the data to

use them in studies based on ordination methods, such as principal components analysis

(Chapter 7), or in studies using multivariate statistics (Chapters 8, 9 and 10).

The name Procrustes comes from Greek mythology; Procrustes fit his visitors (victims)

to a bed by stretching or truncating them. In doing so, Procrustes minimized the difference

between his visitors and the bed. In this sense the comparison is apt; Procrustes superimpo-

sitions minimize differences between landmark configurations. In another sense, the name

does not fit; what Procrustes did altered the shape of his visitors, whereas the mathematical

superimposition methods only use those operations that do not alter shape. Presumably

Procrustes’ guests would have preferred that he had done likewise!

As prescribed in Kendall’s definition of shape (discussed in Chapter 4), Procrustes

superimpositions rely on translation, scaling, and rotation to remove all information

unrelated to shape. However, these operations are used in several other superimposition

methods for the specific reason that they do not change shape. The crucial distinction of

the GLS method is the criterion used to minimize differences between configurations: the

Procrustes distance (the summed squared distances between corresponding landmarks – see

Chapter 4). The particular combination of translation, scaling and rotation that minimizes

the Procrustes distance is considered the optimal Procrustes superimposition. (An interest-

ing historical note on this method is that it was developed before the importance of the

Procrustes distance was fully realized.)

A step-wise description of the GLS method was presented by Rohlf (1990). We sum-

marize each step below; they should be familiar from the previous chapter, in which we

discussed putting shapes into shape space (we also presented the mathematical details of

each operation in that chapter):

1. Center each configuration of landmarks at the origin by subtracting the coordinates

of its centroid from the corresponding (X or Y) coordinates of each landmark. This

chap-05 4/6/2004 17: 23 page 114

114 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

(A)

(B)

(C)

Figure 5.7 Ontogenetic variation in S. gouldingi visualized by three different superimpositions:

(A) Bookstein’s shape coordinates from the 1–7 baseline: (B) sliding baseline registration to the same

baseline; (C) Procrustes superimposition.

chap-05 4/6/2004 17: 23 page 115

SUPERIMPOSITION METHODS 115

translates each centroid to the origin (and the coordinates of the landmarks now reflect

their deviation from the centroid).

2. Scale the landmark configurations to unit centroid size by dividing each coordinate of

each landmark by the centroid size of that configuration.

3. Choose one configuration to be the reference, then rotate the second configuration

to minimize the summed squared distances between homologous landmarks (over all

landmarks) between the forms. In other words, rotate the second configuration to

minimize the partial Procrustes distance.

When there are more than two forms, all are rotated to optimal alignment on the

first; the average shape is then calculated and all are rotated to optimal alignment on the

average shape, which is the new reference. At this point, the average shape is recalculated.

If it differs from the previous reference, the rotations are recalculated using this newest

reference. When the newest reference is the same as the previous, the iterations stop (usually

only a few iterations are necessary). The final reference is the one that minimizes the average

distances of shapes from the reference. Note that this result does not depend on the shape

of the first specimen used in the alignment; instead, it depends on the distribution of shapes

in the sample.

The protocol outlined above has been called partial Procrustes superimposition (Dryden

and Mardia, 1998). The centroid size is set to one for all specimens, so the minimum

distance of a specimen from the reference is the partial Procrustes distance (the length

of the chord connecting fibers in pre-shape space at their points of closest approach –

see Chapter 4). Two steps can be added to the end of this protocol to produce a full

Procrustes superimposition, a method that minimizes the full Procrustes distance: the first

is to compute the full Procrustes distance and corresponding centroid size from the partial

Procrustes distance (this relationship was discussed in Chapter 4); the second is to rescale

each configuration to the new centroid size. The partial Procrustes superimposition is more

commonly used in biological applications, partly because size is held constant, simplifying

the interpretation of shape differences.

The results of the partial Procrustes superimposition (GLS) computed for the piranha

ontogenetic series are compared to coordinates generated by BC and SBR in Figure 5.7.

The coordinates generated by this superimposition are much like those generated from the

two baseline methods when the baseline connected landmarks 1 and 7. These landmarks

are the most distant from the center, so they will tend to have a larger influence than other

landmarks on the rotation to minimize the partial Procrustes distance (a small angular

displacement produces a large linear displacement, which is squared). In addition, the

GLS result appears to be more similar to the SBR result than it is to the BC result. This is

because GLS and SBR both scale each specimen to unit centroid size, so both show relative

deepening as a combination of deepening and shortening.

One advantage of GLS is that the transfer of variance seen in BC is reduced even

more than in SBR. This reduction is partly due to allowing both coordinates of all land-

marks to vary freely (subject to the other constraints of translation, scaling and rotation).

The consequences of this can be seen readily in the pictures of the inferred ontogenetic

transformations of S. gouldingi (Figure 5.8). In BC (Figure 5.8A) the dorsal and ventral

displacements of landmarks are largest, because this is the only way to express deepening

relative to the fixed baseline. In SBR (Figure 5.8B) the dorsal and ventral displacements

chap-05 4/6/2004 17: 23 page 116

116 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

(A)

(B)

(

)

Figure 5.8 Ontogenetic change in S. gouldingi depicted by vectors of relative landmark displacement

computed from three superimpositions: (A) Bookstein’s shape coordinates from the 1–7 baseline;

(B) sliding baseline registration to the same baseline; (C) Procrustes superimposition. Note that the

points that had been anchored to the baseline are displaced ventrally as well as posteriorly.

chap-05 4/6/2004 17: 23 page 117

SUPERIMPOSITION METHODS 117

are reduced, because relative deepening can also be expressed as relative shortening; con-

sequently, landmarks 1 and 7 are shown moving posteriorly and anteriorly respectively.

Both BC and SBR also indicate that the dorsal body deepens faster than the ventral body,

and that several landmarks in the head are displaced dorsally. In GLS (Figure 5.8C) we

see landmarks 1 and 7 moving toward each other as in SBR, but only in GLS do we see

these two landmarks move ventrally relative to all other landmarks. The ventral displace-

ments of these landmarks are an equally valid representation of the greater deepening of

the dorsal body, but one that minimizes the covariance of head and dorsal body land-

marks. This effect is achieved by minimizing the implied displacements of all landmarks

simultaneously.

The more important advantage of GLS is that it is grounded in the mathematical theory

of shape. Configurations of landmarks are manipulated using the three operations that do

not alter shape as defined by Kendall. These operations are used in a manner that removes

all differencesthat are not shape differences. The configurations produced by this procedure

are those that map to points in the shape spaces implied by Kendall’s definition of shape.

The computed distances between these configurations (the various Procrustes distances)

are the distances between points in those spaces, or in certain linear approximations of

those spaces. The characteristics of these metrics are well known, providing a secure and

stable foundation for biological shape analysis.

One of the main disadvantages of GLS is that it yields the full complement of 2K

variable coordinates, which is four more than the number of dimensions of the shape space.

Fortunately, this is a relatively minor problem that can be circumvented rather easily. One

option is to convert the coordinates to the variables discussed in Chapter 6 – the partial

warps scores (the two sets of results will be consistent because both use the same distance

metric). Another option is to use the resampling-based statistical methods discussed in

Chapter 8, which do not require estimates of degrees of freedom. Yet another option is

to use statistical tests specifically adapted to the GLS coordinates (e.g. Goodall’s F-test,

discussed in Chapter 9). Thus the excess number of variable coordinates does not pose an

obstacle to valid statistical analysis.

Another disadvantage is that GLS can yield visually unsettling results, such as rotated

axes of symmetry. For example, analyses of rodent skulls (Zelditch et al., 2003) use

“symmetrized” landmarks on one half of the skull to avoid inflating degrees of freedom

(coordinates for one side are reflected onto the other and the coordinates of the two sides

are averaged for each specimen; see Chapter 3). In the GLS result (Figure 5.9A) the midline

of the skull appears to rotate, but that cannot happen; the midline is the midline regardless

of variation in shape. Not only is this apparent rotation of the midline visually troubling,

it also complicates the interpretation of the results. These are the problems that SBR was

designed to overcome (Figure 5.9B). Because SBR prevents rotation of the baseline, it

yields a more realistic representation of the data – in this case, of the ontogenetic change in

skull shape. Actually, a very similar picture can be obtained by duplicating the landmark

coordinates (except the landmarks on the midline) and reflecting the second set across

the midline, then performing GLS superimposition on the reconstructed whole skulls (Fig-

ure 5.9C). In general, reconstructing the whole skull makes a more interpretable picture

(one that looks more like the organism), so it might be useful to present results in these terms

even if the statistical analyses used the GLS coordinates computed for the symmetrized

half skull.