Zelditch M.L. (и др.) Geometric Morphometrics for Biologists: a primer
Подождите немного. Документ загружается.


chap-04 4/6/2004 17: 22 page 88
88 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS
A numerical example for the simplest case
To make the preceding discussion of theory more concrete and accessible, we apply the
ideas to the simplest useful case, the space of triangles (this space has been discussed
extensively in Small, 1996; Dryden and Mardia, 1998; Rohlf, 2000; Slice, 2001). We have
used this example throughout this chapter, but we now pull all the information together.
There are other approaches to constructing the matrices representing shapes in Kendall’s
shape space, but the sequence of steps we follow here is easily illustrated and requires
relatively simple computations.
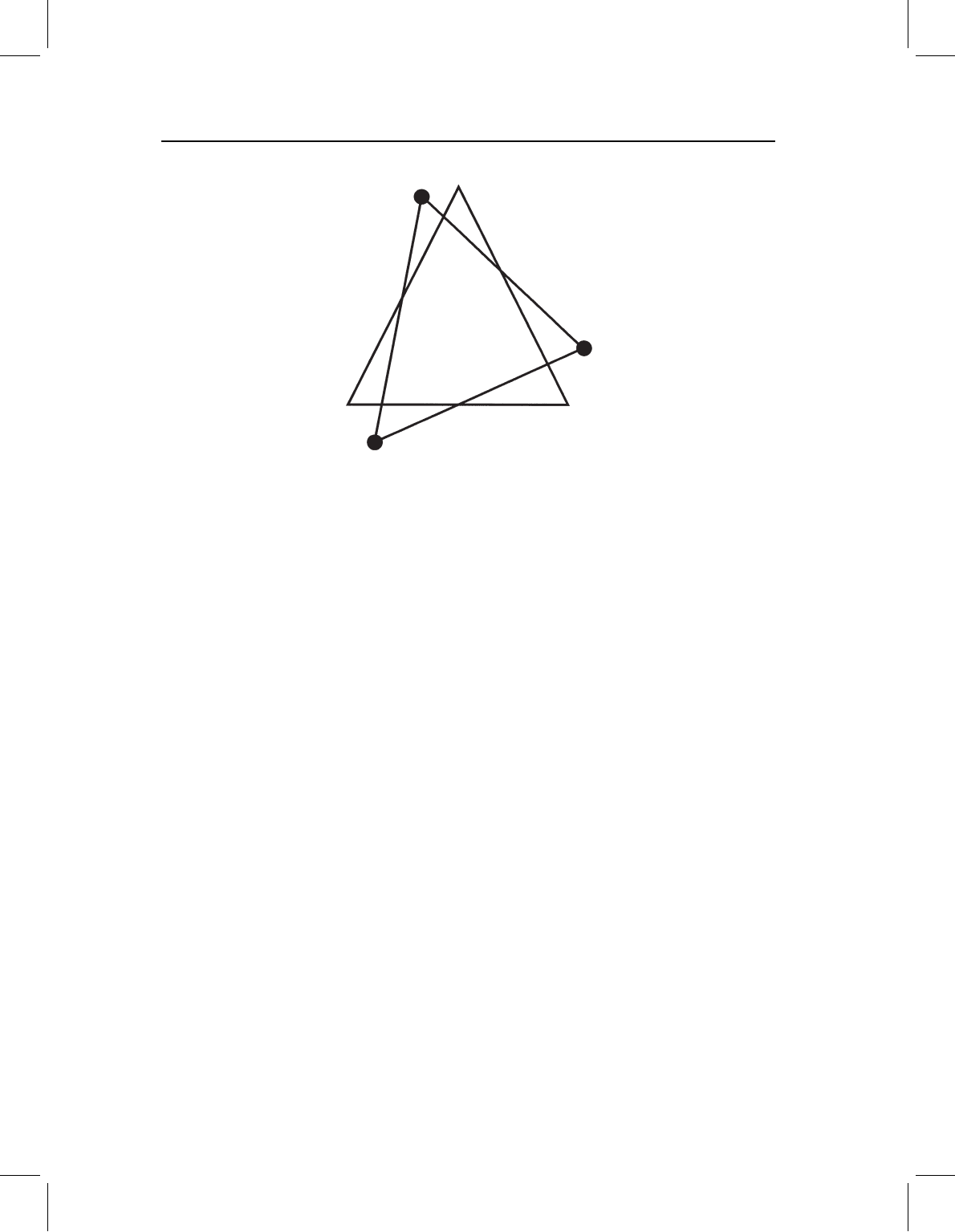
We begin with two triangles, X and W, drawn on a flat surface (Figure 4.12). X
is the triangle from Figure 4.2, with coordinates (−1, −1), (1, −1) and (0, 1); triangle
W has coordinates (1.07, −1.64), (3.10, −0.72) and (1.55, 0.82). Each triangle has K =3
landmarks with M =2 coordinates; thus the configuration matrix for each has six entries:
X =
−1 −1
1 −1
01
W =
1.07 −1.64
3.10 −0.72
1.55 0.82
(4.14)
The six landmark coordinates of each triangle contain six pieces of information needed to
determine all the properties of that triangle: size, shape, location, and rotation. Not only
do we need all six coordinates to determine these properties; we cannot infer the value of
any one coordinate from the other five. Because we need all six coordinates to determine
the triangle, we can say there are six degrees of freedom. This also helps to explain why
the configuration space of triangles has six dimensions.
We can infer from the coordinates that the two triangles have different locations, as
suggested in the figure. We confirm this by calculating the coordinates of the centroid
1
3
X
W
2
3
1
2
Figure 4.12 Two triangles, X (from Figure 4.2) and W. The vertices are numbered to indicate their
homologies.

chap-04 4/6/2004 17: 22 page 89
THEORY OF SHAPE 89
using Equation 4.5, reproduced here:
X
C
=
1
K
K
j=1
X
j
(4.15)
Y
C
=
1
K
K
j=1
Y
j
For triangle X, the coordinates of the centroid are X
C
=(1/3)(−1 +1 +0) =0, and
Y
C
=(1/3)(−1 +−1 +1) =−0.333. For triangle W, the coordinates of the centroid are
X
C
=(1/3)(1.07 +3.10 +1.55) =1.907 and Y
C
=(1/3)(−1.64 +−0.72 +0.82) =−0.513.
We use the coordinates of the centroid to form the centered configuration matrix XC by
subtracting the centroid coordinate from the corresponding coordinate of each landmark:
XC =
(X
1
−X
C
)(Y
1
−Y
C
)
(X
2
−X
C
)(Y
2
−Y
C
)
.
.
.
.
.
.
(X
K
−X
C
)(Y
K
−Y
C
)
(4.16)
This produces the centered configuration matrices:
X
centered
=
(−1 −0) (−1 −(−0.333))
(1 −0) (−1 −(−0.333))
(0 −0) (1 −(−0.333))
=
−1 −0.667
1 −0.667
01.333
(4.17)
and
W
centered
=
(1.07 − 1.907) (−1.64 − (−0.513))
(3.10 −1.907) (−0.72 −(−0.513))
(1.55 −1.907) (0.82 −(−0.513))
=
−0.837 −1.127
1.193 −0.207
−0.357 1.333
(4.18)
The centered triangles are shown in Figure 4.13. One consequence of centering is that
the two triangles are now superimposed; another is the loss of two degrees of freedom.
Knowing that the centroid has coordinates (0, 0), which are the means of the landmark
coordinates, we can use the coordinates of any two landmarks to determine the coordinates
of the third landmark. Accordingly, the space of centered triangles (which we have not
discussed previously) is a four-dimensional space. Another way to think of this is that the
two coordinates of the centroid, specifying the location of the triangle, account for two of
the six dimensions of the configuration space. Also, now that all individuals have the same
value for their centroid coordinates, the variation due to position disappears, collapsing
that dimension of variation to a point at the origin.
The centered triangles are not in pre-shape space. To put them there, we need to rescale
each so that its centroid size is one. The formula for centroid size is:
CS(X) =
K
i=1
M
j=1
(X
ij
−C
j
)
2
(4.19)

chap-04 4/6/2004 17: 22 page 90
90 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS
3
X
W
1
2
1
2
3
Figure 4.13 Centered triangles computed from X and W. Computation of the centroids of X and
W is given by Equation 4.15; computation of the landmark coordinates after centering is given by
Equations 4.16–4.18. Vertices are numbered to indicate their homology.
which is the square root of the sum of the squared distances of the landmarks from the
centroid. Given that the centroids of X
centered
and W
centered
are both at (0, 0), we can simply
sum the squared coordinates:
CS(X
centered
) =
(−1.0)
2
+(−0.667)
2
+(1.0)
2
+(−0.667)
2
+(0)
2
+(1.333)
2
= 2.160 (4.20)
CS(W
centered
) =
(−0.837)
2
+(1.127)
2
+(1.193)
2
+(−0.207)
2
+(−0.357)
2
+(1.333)
2
= 2.311 (4.21)
Dividing each coordinate of the centered triangle by its centroid size produces the pre-shape
matrices:
X
pre-shape
=
1
2.160
−1 −0.667
1 −0.667
01.333
=
−0.463 −0.309
0.463 −0.309
0.000 0.617
(4.22)
W
pre-shape
=
1
2.311
−0.837 −1.127
1.193 −0.207
−0.357 1.333
=
−0.362 −0.488
0.516 −0.089
−0.154 0.577
(4.23)
These centered and scaled triangles are shown in Figure 4.14.
Because size differences do not contribute to the differences between X
pre-shape
and
W
pre-shape
, another degree of freedom has been lost (this is the third degree of freedom
chap-04 4/6/2004 17: 22 page 91
THEORY OF SHAPE 91
3
X
W
1
2
1
2
3
Figure 4.14 Centered triangles from Figure 4.13, scaled to unit centroid size. Computation of
centroid size is given in Equations 4.19–4.21. Computation of landmark coordinates after scaling is
given by Equations 4.22 and 4.23.
lost). In other words, size is no longer a dimension of possible variation; configurations
that differ only in size are considered equivalent. After subtracting the three degrees of free-
dom representing differences in location and centroid size, we are left with three degrees
of freedom to describe differences among triangle pre-shapes – triangles that are cen-
tered and scaled to unit centroid size. Accordingly, the pre-shape space of triangles is
a three-dimensional space. As explained above, it is the three-dimensional surface of a
four-dimensional hypersphere, so it is not an easy space to visualize or illustrate.
To make the transition from pre-shape space to shape space, we begin by choosing one
shape and placing it in a convenient orientation; this configuration will be the reference.
For this demonstration it is convenient to use X in the orientation shown in the last few
figures. Choosing X as the reference means that W will be the target, so the next step is to
rotate W, in the plane of the page around its centroid through some angle (θ). The rotation
places it in the orientation that minimizes the difference between the two sets of landmark
coordinates (Figure 4.15). After the rotation, the X- and Y-coordinates of each landmark
will be mapped to the new coordinates (X cos θ −Y sin θ), (X sin θ +Y cos θ). Thus, the
rotated form of W
pre-shape
will be:
W
pre-shape, rotated
=
(−0.362 cos θ) − (−0.488 sin θ)(−0.362 sin θ) +(−0.488 cos θ)
(0.516 cos θ) − (−0.089 sin θ)(0.516 sin θ) +(−0.089 cos θ)
(−0.154 cos θ) − (0.577 sin θ)(−0.154 sin θ) + (0.577 cos θ)
(4.24)
Before we can pick the value of θ that will minimize the difference between the reference
(X
pre-shape
) and the rotated target (W
pre-shape, rotated
), we need a criterion to define what is
being minimized. The criterion that leads to the shape space discussed earlier is minimiza-
tion of the square root of the sum of the squared distances between the corresponding
chap-04 4/6/2004 17: 22 page 92
92 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS
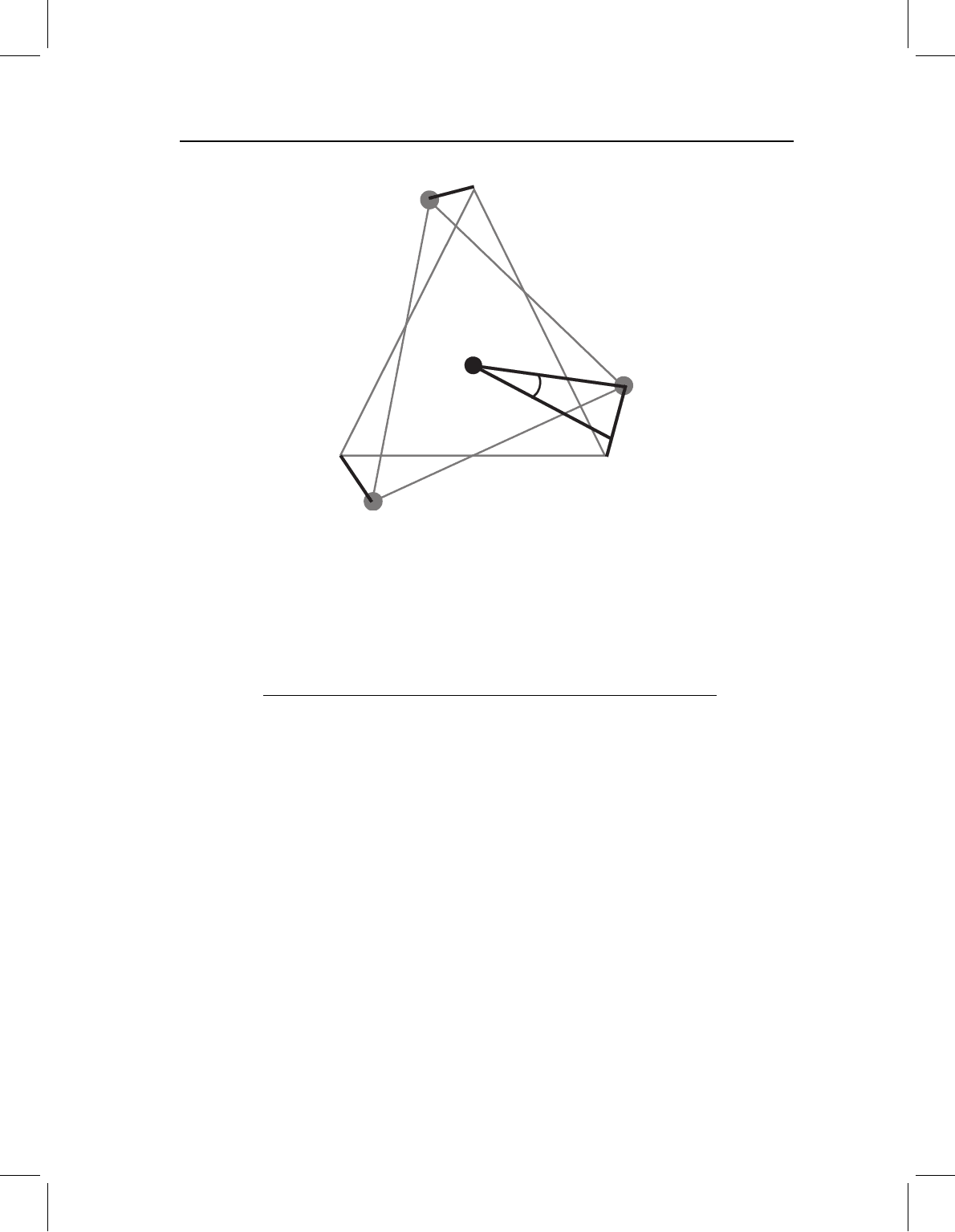
X
W
u
d
1
d
3
d
2
Figure 4.15 Optimal alignment of W to X will be achieved by rotating W around its centroid
through an unknown angle θ to minimize the square root of the sum of the squares of distances d
1
,
d
2
, and d
3
.
landmarks (the distances d
1
, d
2
, and d
3
shown in Figure 4.15). This quantity can be com-
puted directly from the squared differences between the corresponding coordinates of the
landmarks:
D =
(X
11
−X
21
)
2
+(Y
11
−Y
21
)
2
+···+(X
13
−X
23
)
2
+(Y
13
−Y
23
)
2
(4.25)
(There are other criteria that lead to other superimpositions of the two triangles; one is
discussed below, others in Chapter 5.)
With this criterion in hand, we can solve for the unique value of θ at which D is
minimized. In our example, that value is θ =−19.2
◦
. When we insert this value into the
matrix for W
pre-shape, rotated
(Equation 4.22), we get:
W
pre-shape, rotated
=
−0.502 −0.341
0.458 −0.254
0.044 0.596
(4.26)
Under the conditions set out above, this is the optimal alignment to the reference form:
X
pre-shape
=
−0.463 −0.309
0.463 −0.309
0.000 0.617
(4.27)
Figure 4.16 shows the two triangles under these conditions.
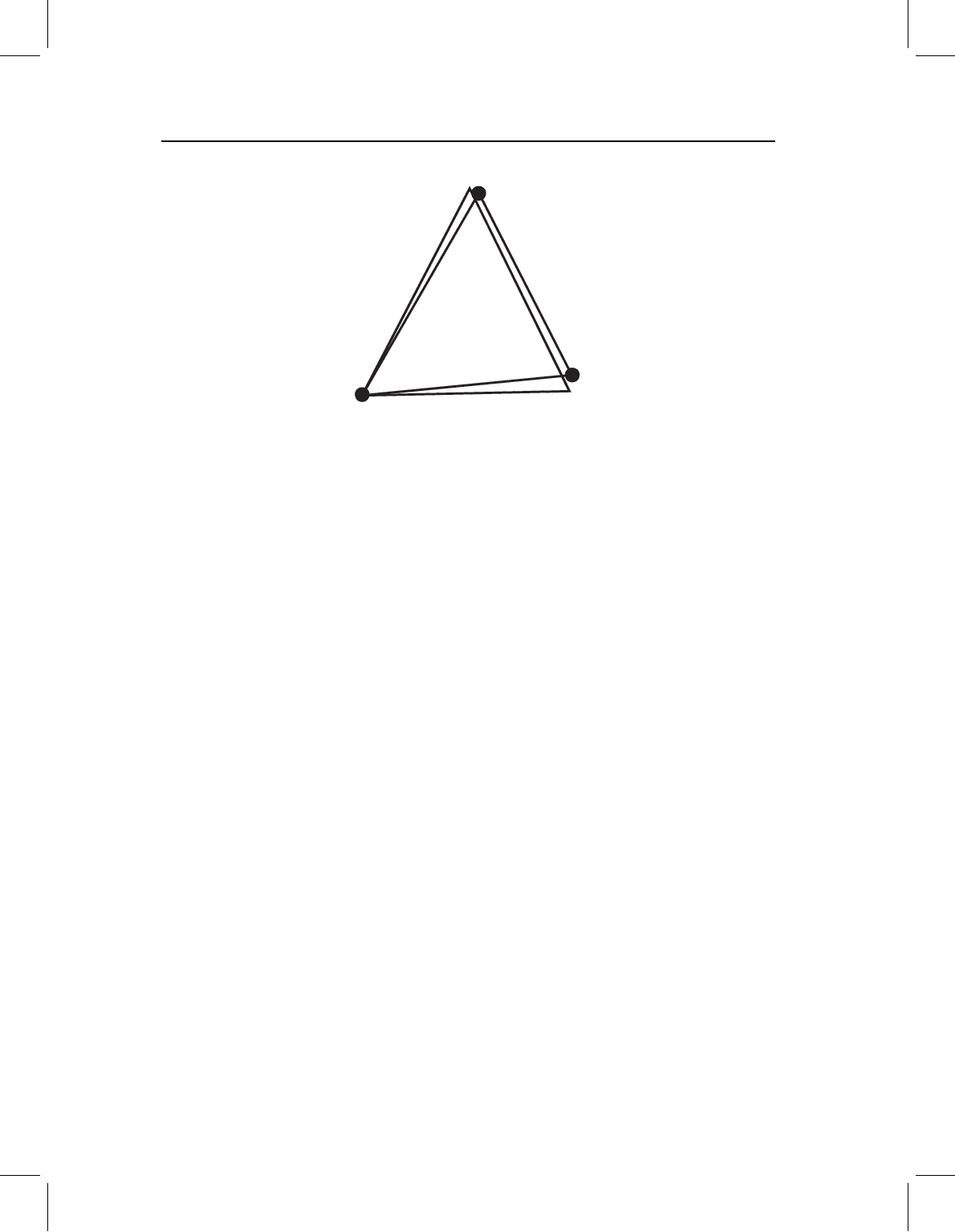
chap-04 4/6/2004 17: 22 page 93
THEORY OF SHAPE 93
X
W
1
2
3
Figure 4.16 Triangles X and W after rotation of W to minimize the Procrustes distance. Compu-
tation of the landmark coordinates of W after rotation is given in Equation 4.24; the result is given
in Equation 4.26. Vertices are numbered to indicate their homology.
The distance minimized above is the partial Procrustes distance, so we will label it D
p
from this point forward. The value of D
p
in this particular case is:
D
p
= [(−0.502 −(−0.463))
2
+(−0.341 −(−0.309))
2
+ (0.458 −0.463)
2
+(−0.254 −(−0.309))
2
+ (0.044 −0)
2
+(0.596 −0.617)
2
]
½
= 0.089 (4.28)
This is the minimum length of the chord connecting the pre-shape fibers of X and W in
the pre-shape space of triangles. Because W is superimposed to meet the criterion of min-
imizing the partial Procrustes distance, W
pre-shape, rotated
is said to be in partial Procrustes
superimposition on the reference form X
pre-shape
. We can solve for the Procrustes distance,
the arc length across the surface between X
pre-shape
and W
pre-shape, rotated
, because the radius
of the hypersphere is constrained to be one. The perpendicular from the chord to the center
of the hypersphere bisects the angle ρ (Figure 4.17), which has the same value (in radians)
as the arc length. Thus, there is a very simple relationship between D
p
and ρ; specifically,
ρ =2 arcsin(D
p
/2). In our example, D
p
and ρ are so small they cannot be distinguished with
fewer than 4 decimal places (0.08941 and 0.08943, respectively), which is not surprising
given that ρ represents a very small angle of just 5.1
◦
.
Because rotational effects do not contribute to the differences between X
pre-shape
and
W
pre-shape, rotated
, another degree of freedom has been lost (the fourth). Rotation, or ori-
entation, is no longer a dimension of possible variation; configurations that differ only by
rotation are considered equivalent. After subtracting the four degrees of freedom repre-
senting differences in location and centroid size and rotation, we are left with two degrees
of freedom to describe differences among triangles. Accordingly, the shape space of trian-
gles is a two-dimensional space. As explained above, it is the two-dimensional surface of
a three-dimensional sphere, and is a relatively easy space to visualize or illustrate.
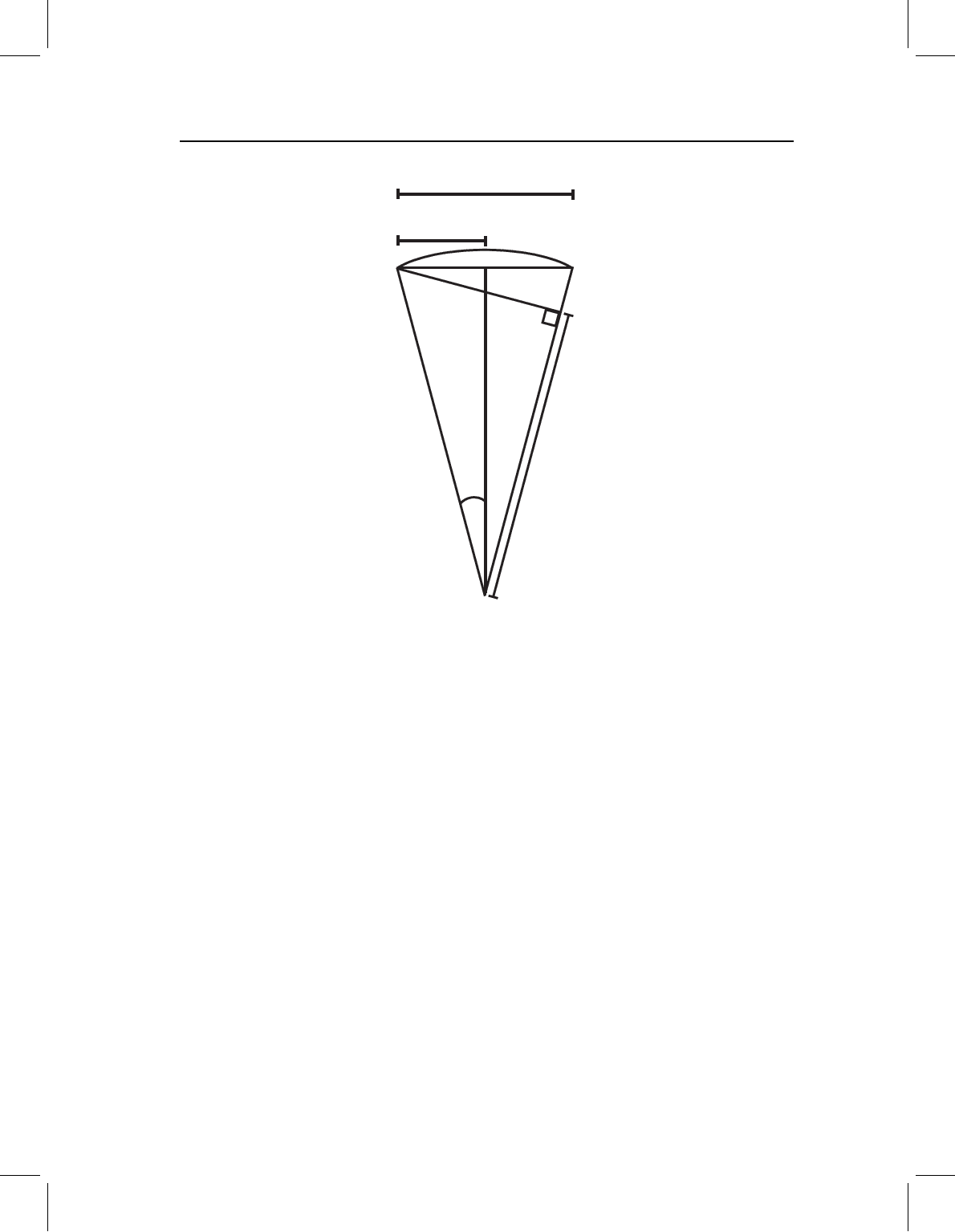
chap-04 4/6/2004 17: 22 page 94
94 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS
D
p
r/2
D
F
cos(r)
sin(r/2)
W
B
X
Figure 4.17 The relationships among the Procrustes distance, ρ, full Procrustes distance
D
F
=sin(ρ), and partial Procrustes distance D
p
=2 sin(ρ/2). The configuration at point B represents
a triangle in Kendall’s shape space.
X
pre-shape
and W
pre-shape, rotated
are configurations in a shape space, but they are not yet
in Kendall’s shape space. To make this final transition, we need to solve for the centroid
size that would further reduce the distance between the shapes X and W; we are taking
W to B (Figure 4.17). As indicated in Figure 4.17, that distance (D
F
, the full Procrustes
distance) is measured along a line segment orthogonal to the radius of W
pre-shape, rotated
,
passing through X
pre-shape
. In our example, ρ is small (0.0894 radians); its cosine is near
one (0.996) so we need make only a very slight adjustment to convert the coordinates of
W
pre-shape, rotated
to W
shape
:
W
shape
= cos(0.089)
−0.5021 −0.3414
0.4583 −0.2542
0.0439 0.5956
=
−0.5001 −0.3401
0.4564 −0.2532
0.0437 0.5932
(4.29)
This is the triangle with the same shape as W, but it is now in Kendall’s shape space with the
reference at triangle X
pre-shape
. Because the full Procrustes distance was used to determine
the coordinates of the landmarks in W
shape
, we can say that W
shape
is in full Procrustes
superimposition on the reference form X
pre-shape
.
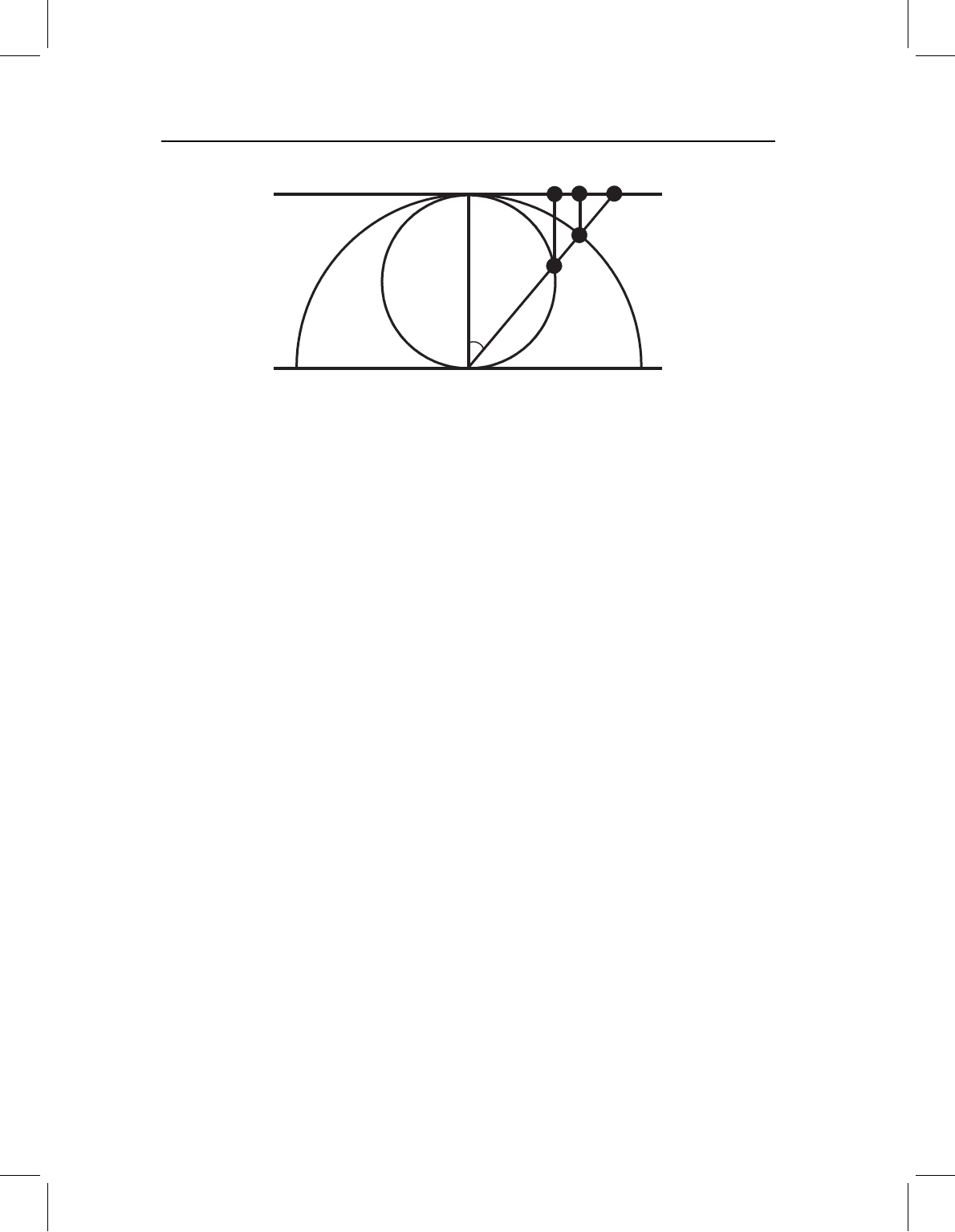
chap-04 4/6/2004 17: 22 page 95
THEORY OF SHAPE 95
r
(
0, 0
)(
1, 0
)(
⫺1, 0
)
A
B
CDE
Tangent plane
Figure 4.18 Tangent space to shape spaces of triangles and projections onto the tangent space. As
in Figure 4.11, the outer hemisphere is a section through the space of centered and aligned shapes
scaled to unit centroid size, and the inner circle is a section through Kendall’s shape space of centered
and aligned shapes scaled to cos(ρ). The plane is tangent to the sphere and the hemisphere at the
point of the reference shape. The configuration at point B represents a triangle in Kendall’s shape
space; A is the same shape scaled to unit centroid size. C is a stereographic projection of B onto the
tangent plane. D is the orthogonal projection of A onto the tangent plane, and E is the orthogonal
projection of B onto the tangent plane.
Tangent spaces
As mentioned earlier in this chapter, the mathematics of statistical inference in Kendall’s
shape space has been developed by Kendall and others. However, the simple fact remains
that the curvature of shape space makes statistical inference more difficult in this space
than it is in Euclidean spaces. In addition, most of the familiar methods of multivariate
statistical analysis assume a Euclidean space. Therefore, in this section we discuss the
replacement of Kendall’s shape space with a Euclidean approximation.
The problem of replacing a curved space with a Euclidean approximation is illustrated
for the special case of triangles in Figure 4.18. As before (see Figure 4.11), the outer
hemisphere is the space constructed by aligning pre-shapes (with centroid size fixed at
one) to minimize the partial Procrustes distance (the square root of the summed squared
distances between corresponding landmarks). The inner sphere is Kendall’s shape space,
constructed by scaling the aligned target shapes to centroid size =cos(ρ). These two spaces
share a common point, the reference shape, because the distance of the reference from
itself is zero, so cos(ρ) is one. Tangent to both of these spaces, at the reference shape,
is a Euclidean plane. We also need to decide how we will construct the projection of
shapes onto the tangent plane, which includes deciding (1) which space will be the source
of the configurations projected onto the tangent plane, and (2) what rule we will use
to determine the direction of the projection. (We also need to decide how to choose an
appropriate reference configuration to serve as the tangent point, which is discussed in the
next section.)
Figure 4.18 illustrates two common approaches to projecting from one space onto
another. One approach is to project to the new space from the centroid of some reference
space. In this case, the reference space is the hemisphere of aligned pre-shapes, so the

chap-04 4/6/2004 17: 22 page 96
96 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS
projections are along the radii of this hemisphere to the tangent space. In this stereographic
projection, the shape represented by points B and A (at centroid sizes cos(ρ) and one,
respectively) map to the same location (C) in the tangent space. The distance in the plane
from the reference to C is greater than the arc length from the reference to B (the Procrustes
distance); and the discrepancy between these distances increases as ρ increases and the
distance in the tangent plane approaches infinity. The other approach to projecting from
one space onto another is to project along lines that are orthogonal to the new space. Point
E represents the orthogonal projection of B onto the tangent plane, and this projection
produces distances from the reference in the tangent plane that are less than the Procrustes
distance. As in the stereographic projection, the magnitude of the discrepancy between the
distances increases as ρ increases, but in the orthogonal projections, distances in the tangent
plane asymptotically approach the maximum equal to the radius of the shape space.
In the stereographic projection it does not matter whether the projection to the tan-
gent plane is from the hemisphere of triangles in partial Procrustes superimposition, or
from the sphere of triangles in full Procrustes superimposition. Both target configurations
project to the same point in the tangent space. In the orthogonal projection, it does matter
whether the projection from the tangent plane is from the outer or inner hemisphere. The
projection from the hemisphere produces distances in the tangent plane that depart less
from the Procrustes distance (the arc length) and are closer to the partial Procrustes dis-
tance (the chord length). Projection from the sphere produces distances that depart more
from the Procrustes distance and are closer to the full Procrustes distance. Furthermore,
the projections from the hemisphere of triangles in partial Procrustes superimposition have
a higher maximum distance from the reference (one instead of one-half), and approach it
more slowly.
In the simple example given in the previous section, we demonstrated that the differences
between the Procrustes, partial Procrustes and full Procrustes distances from the reference
become negligible as ρ approaches zero. Similarly, the differences among the stereographic
and orthogonal projects also become negligible as ρ approaches zero.
Selecting the reference configuration
Many of the steps involved in placing target configurations in shape space, or in the
Euclidean space tangent to it, are functions of the reference shape. For example, in the
construction of a shape space, each target configuration is rotated to the orientation that
minimizes its distance from the reference. Also, in the construction of Kendall’s shape
space, the scaling of each target configuration is a function of its distance from the reference.
Moreover, the tangent space is tangent to shape space at the reference. Perhaps most
important, the discrepancies between distances in the tangent space and those in shape
space increase as a function of distance between target and reference. Thus the choice of
reference can have important consequences.
Most interesting biological questions will be concerned with differences among more
than two specimens. The inferences based on analyses of multiple specimens will be based
on all of the distances among specimens, not just their distances from the reference. Accord-
ingly, the choice of a reference must consider the effects of that choice on approximating
distances among target specimens, not just distances of target specimens from the reference.

chap-04 4/6/2004 17: 22 page 97
THEORY OF SHAPE 97
Not only will distances from the reference be distorted, so too will the distances among
target specimens, and this distortion will also be a function of their distances from the ref-
erence. If these distortions are large, inferences based on distances in the Euclidean tangent
space will be unreliable.
One possible reference is the average shape of the entire sample (computed using meth-
ods discussed in Chapter 5). This approach has the advantage that it minimizes the average
distance from the reference, which minimizes the average distortions of interspecimen dis-
tances projected to the tangent plane (Bookstein, 1996; Rohlf, 1998). An alternative choice
of reference is a shape inferred to represent the starting point of some biological process
(e.g. a neonate in a study of ontogenetic transformation – cf. Zelditch et al., 1992). This
approach has the advantage that the difference between target and reference can be inter-
preted as a biological transformation as well as a mathematical transformation (Fink and
Zelditch, 1995; Zelditch et al., 1998). However, as Rohlf (1998) points out, this approach
can have the limitation that the reference is at one extreme of the observed distribution
of shapes, thereby increasing the risk of substantial distortions of distances when changes
in shape are large. Conceivably, erroneous inferences could be drawn from the analysis.
However, Marcus et al. (2000) analyzed differences in skull shape among representa-
tives of several mammalian orders and found that most Procrustes distances are closely
approximated by the Euclidean distance in the tangent space. The principal exceptions
were the distances from terrestrial taxa (especially the muskrat) to a dolphin (which is
not surprising, given the extraordinary reorganization of the cetacean head). This result
suggests that most biologists are unlikely to encounter any cases in which the differences
among specimens are large enough to worry about the adequacy of the linear approxima-
tions. It is unlikely that distances in the tangent space (based on any reference) will poorly
approximate distances in shape space. Even so, using the average shape of all specimens in
the data minimizes the risk that such a problem will occur. The use of any other reference
carries with it the responsibility to ensure that Euclidean distances in the tangent space are
accurate approximations of the distances in shape space.
Dimensions and degrees of freedom
The issue of degrees of freedom (or the number of independent measurements in a system)
is important for statistical analyses, but it can be confusing, especially when talking about
shape. To clarify it, we can consider a simple example. Suppose we wish to describe the
location of a notebook in a room. We could give its location in terms of three distances
from a reference point (such as the corner of the door of the room), and this is equivalent to
defining its position by three Cartesian coordinates relative to that reference point. In this
example, there are three degrees of freedom for the location of the notebook because three
variables are required to describe it. Knowing those variables and the reference suffices to
find the notebook. However, if the notebook is on a chair, and all chairs are known to
be the same height, specifying the height conveys no more information than saying that
the notebook is on a chair. Knowing what we do about the chairs, we only need two
additional pieces of information, the X- and Y-coordinates, to specify the location of the
notebook in the room. Thus by specifying the constraint that the notebook is on a chair
of fixed height, we have removed one of the three degrees of freedom.
