Zelditch M.L. (и др.) Geometric Morphometrics for Biologists: a primer

Подождите немного. Документ загружается.

chap-04 4/6/2004 17: 22 page 78

78 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

1, ⫺1

0, 1

⫺1, ⫺1

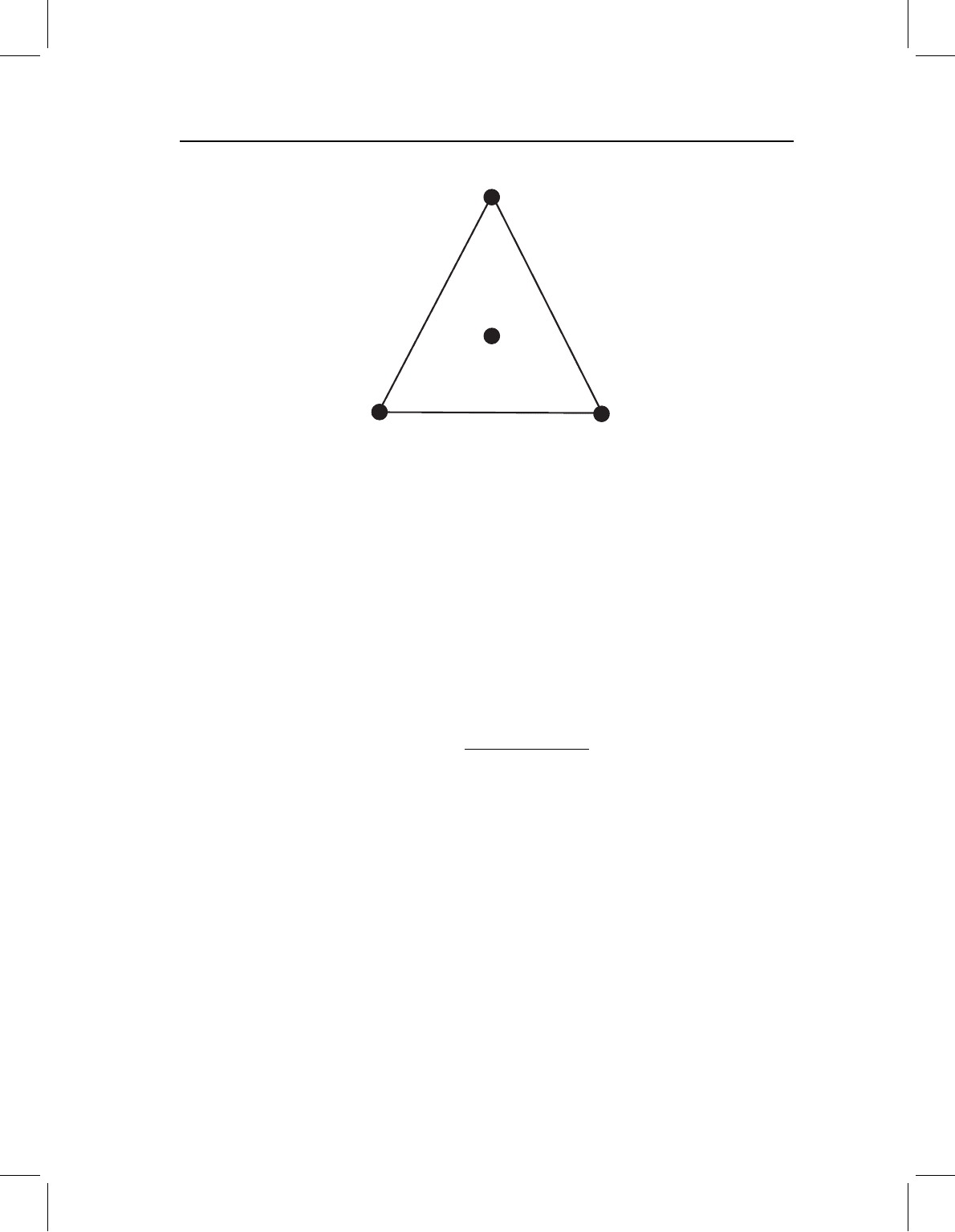
Centroid

(0.0, ⫺0.333)

Figure 4.3 The centroid of the triangle in Figure 4.2. The coordinates of the centroid are the

averaged coordinates of the three vertices.

Size of a configuration matrix

Before we can coherently talk about scale, we need to define what we mean (mathemati-

cally) by the term size. For configuration matrices, a number of different, non-equivalent

size measures have been used. It is not possible to say that one size measure is “correct” or

“preferable,” but it is important to explain the consequences of making a particular choice.

The most commonly used size measure in geometric morphometrics is called centroid size,

which is favored because it does not induce a correlation between size and shape, hence

we restrict our discussion of size to that particular measure.

The centroid size (CS) of a configuration (X) is:

CS(X) =









i=1



j=1

−C

)

(4.7)

where the sum is over the rows i and columns j of the matrix X. X

is a standard notation

from linear algebra specifying the value located on the ith row and jth column of the matrix

X, and in this case C

stands for the location of the jth component of the centroid. C

the X-coordinate of the centroid and C

is its Y-coordinate.

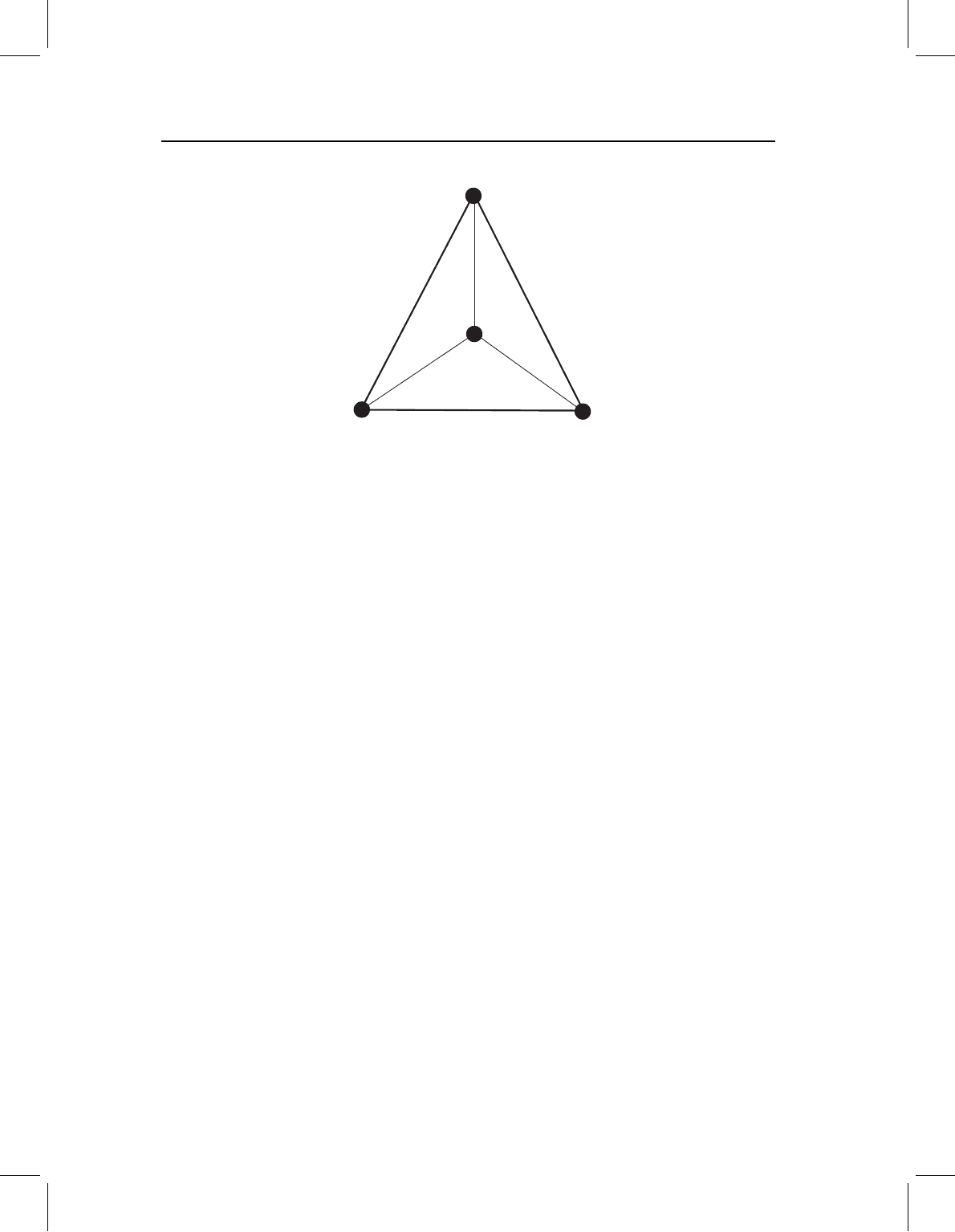
Centroid size is thus the square root of the sum of the squared distances of the landmarks

from the centroid. The distances from the centroid to each landmark of the triangle are

shown in Figure 4.4; the centroid size of this triangle is simply the square root of the sum

of the squared lengths of these lines. Centroid size is not altered by changing the position

of the configuration, because this leads to all landmarks (and the centroid) changing by a

common amount. Similarly, multiplying the configuration matrix X by a constant factor

increases centroid size by the same factor. Two configurations of landmarks that differ

only in centroid size do not differ in shape (they differ only in scale).

chap-04 4/6/2004 17: 22 page 79

THEORY OF SHAPE 79

1, ⫺1

0, 1

⫺1, ⫺1

Figure 4.4 Centroid size of the triangle in Figure 4.2, calculated as the sum: (L1

+L2

)

1/2

=2.16.

Pre-shape space

As we stated above, every configuration of K landmarks having M coordinates can be

thought of as a point in a space with K ×M dimensions. (To avoid confusion, we should

make it clear that by “point” in this context we mean an individual shape, an entire

configuration of landmarks, not one landmark.) Some of the configurations in this space

differ only in centroid size; others differ only in location (coordinates of the centroid). We

can define a subset of configurations that do not differ in location or size by placing two

restrictions on each configuration matrix: (1) that it be centered, and (2) that centroid

size be one. These restrictions define a space called pre-shape space (Dryden and Mardia,

1998). In practice, we translate and scale each of the original configurations in our data so

that the new configurations meet the restrictions of pre-shape space. In doing this, we are

using two of the three operations that do not alter shape. Each of the new configurations

is a centered pre-shape.

The shape of pre-shape space

The two requirements imposed on this space mean that the summed squared landmark

positions add up to one. The consequences of that property can be understood by consid-

ering the set of points satisfying the restriction in an ordinary two-dimensional space: the

set of points is centered on the origin (0, 0), and each point in the set has coordinates satis-

fying the equation X

=1. The set of points is a circle of radius one, centered on the

origin. This circle is a one-dimensional subspace (a curve) inhabiting a two-dimensional

space (a plane). Knowing that all points are equidistant from the center means that we need

specify only the direction of a point from the center to define it uniquely; thus, the location

of any point on the circle can be described sufficiently by a single dimension (direction).

Extending this to a three-dimensional space, we now have the set of all points (X, Y, Z)

centered on the origin (0, 0, 0) such that X

=1. This is the surface of a sphere

chap-04 4/6/2004 17: 22 page 80

80 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

of radius one, centered on the origin, and it is a two-dimensional subspace within a three-

dimensional space. Again, the constraint that all points are on the surface allows us to

describe the location of a point by giving a direction from the center; the only difference

from the circle is that we now need two components to describe that direction (e.g. latitude

and longitude). So in talking about a pre-shape space we are talking about the surface of

a hypersphere centered on the origin, which is the generalization of an ordinary sphere in

K ×M dimensions. In that general case, we have:



i=1



j=1

)

= 1(4.8)

which states that the sum of all squared landmark coordinates is one. That hypersphere is

simply the equivalent of a sphere in more than three dimensions.

We can determine the number of dimensions in pre-shape space by considering the num-

ber of dimensions that were lost in the transition from configuration space. One dimension

is lost in fixing centroid size to one, eliminating the size dimension of the configuration

space. Another, M dimensions are lost in centering the configurations; eliminating the M

dimensions needed to describe location (the coordinates of the centroid). Thus in moving

from configuration space to pre-shape space, we moved to a space that has M +1 fewer

dimensions, which is:

KM −(M +1) =KM −M −1(4.9)

For two-dimensional configurations of landmarks, pre-shape spaces have 2K −3 dimen-

sions; so the pre-shape space for triangles has three dimensions. For three-dimensional

configurations of landmarks, pre-shape spaces have 3K −4 dimensions.

Returning to the three-dimensional sphere (because most of us have trouble imagining

spaces having more than three dimensions), you should be imagining pre-shape space to be

a hollow ball of radius one, centered at the origin (0, 0, 0). Arrayed on the two-dimensional

surface of this ball are points representing individual configurations of landmarks. The two

restrictions we have imposed on our configuration matrices mean that the configurations

in this set do not differ in scale or location; we have used the operations of translation and

scaling to remove the effects of (differences in) location and scale. We have not yet rotated

the shapes to remove the effects of rotation (that comes later, as we move from pre-shape

space to shape space). Thus, configurations of landmarks that differ only by a rotation

are located at different points in pre-shape space, as are configurations that differ only in

shape. This underscores an important point (which some may find counterintuitive): as we

said earlier, configurations that differ only by a rotation (such as those shown in Figure

4.1B) do not differ in shape. Because we have not yet removed all three effects mentioned

in Kendall’s definition of shape (location, scale and rotation) we have not yet reached

shapes. At present we are concerned with pre-shapes, i.e. configurations that may differ

by a rotation, by a shape change or by some combination of the two. In pre-shape space,

configurations that differ only by rotation are different points, as are configurations that

differ only in shape.

chap-04 4/6/2004 17: 22 page 81

THEORY OF SHAPE 81

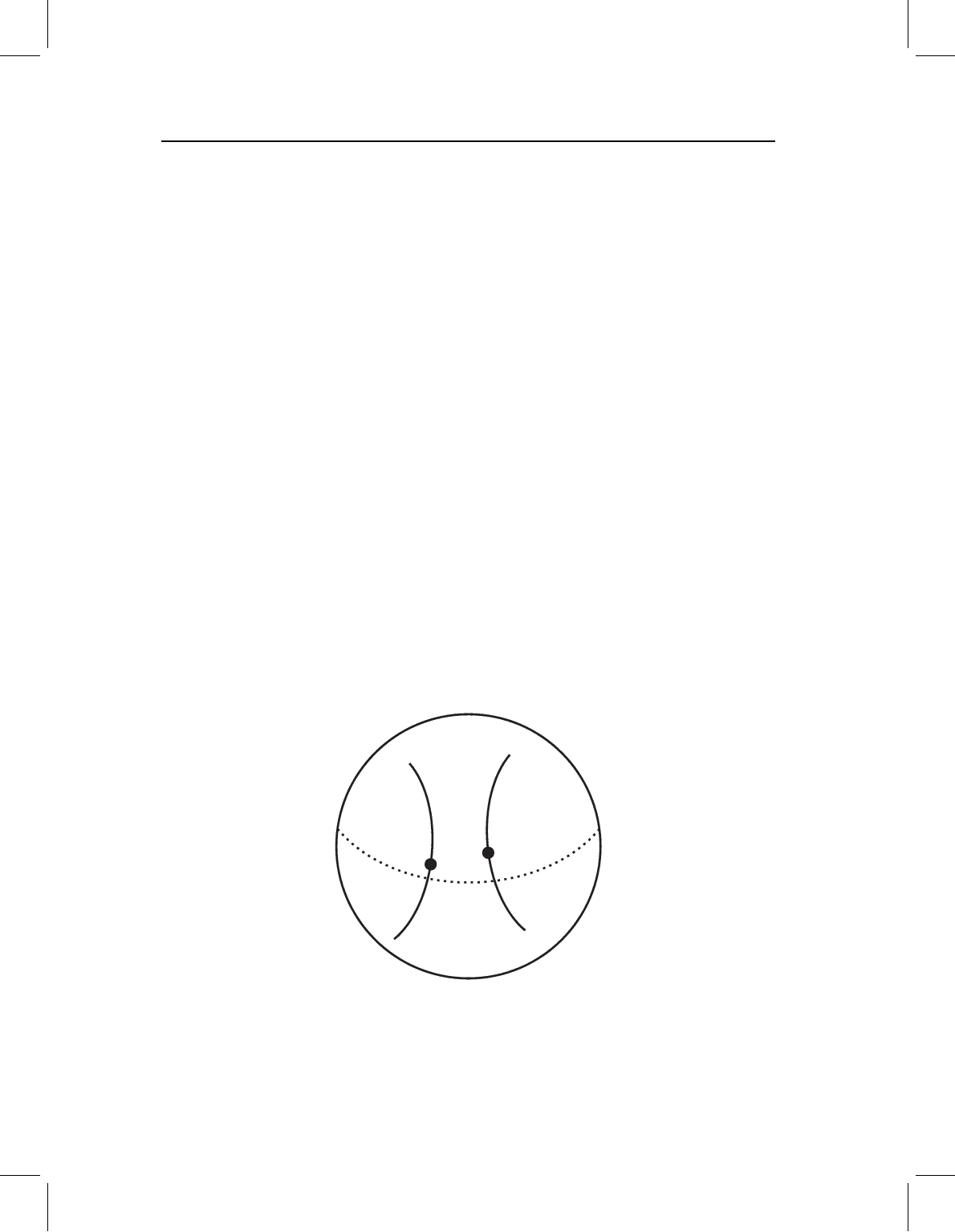
Fibers in pre-shape space

To visualize the locations in pre-shape space of configurations that differ only in rotation,

we introduce the term fiber. A fiber (in the context of our particular discussion of pre-

shape space) consists of the set of all the points in pre-shape space that can be obtained by

rotating a particular centered pre-shape. The fiber is a circular arc that comprises the set

of all points in pre-shape space that can be “reached” by rotating the pre-shape matrix.

Figure 4.5 depicts the concept of fibers as an arc on the surface of a sphere (ignoring the

higher dimensionality of a pre-shape hypersphere). Two fibers are shown: arcs 1 and 2.

Arc 1 is the set of all possible rotations of the pre-shape Z

, and arc 2 is the set of all

possible rotations of the pre-shape Z

. For a less abstract visualization of the concept

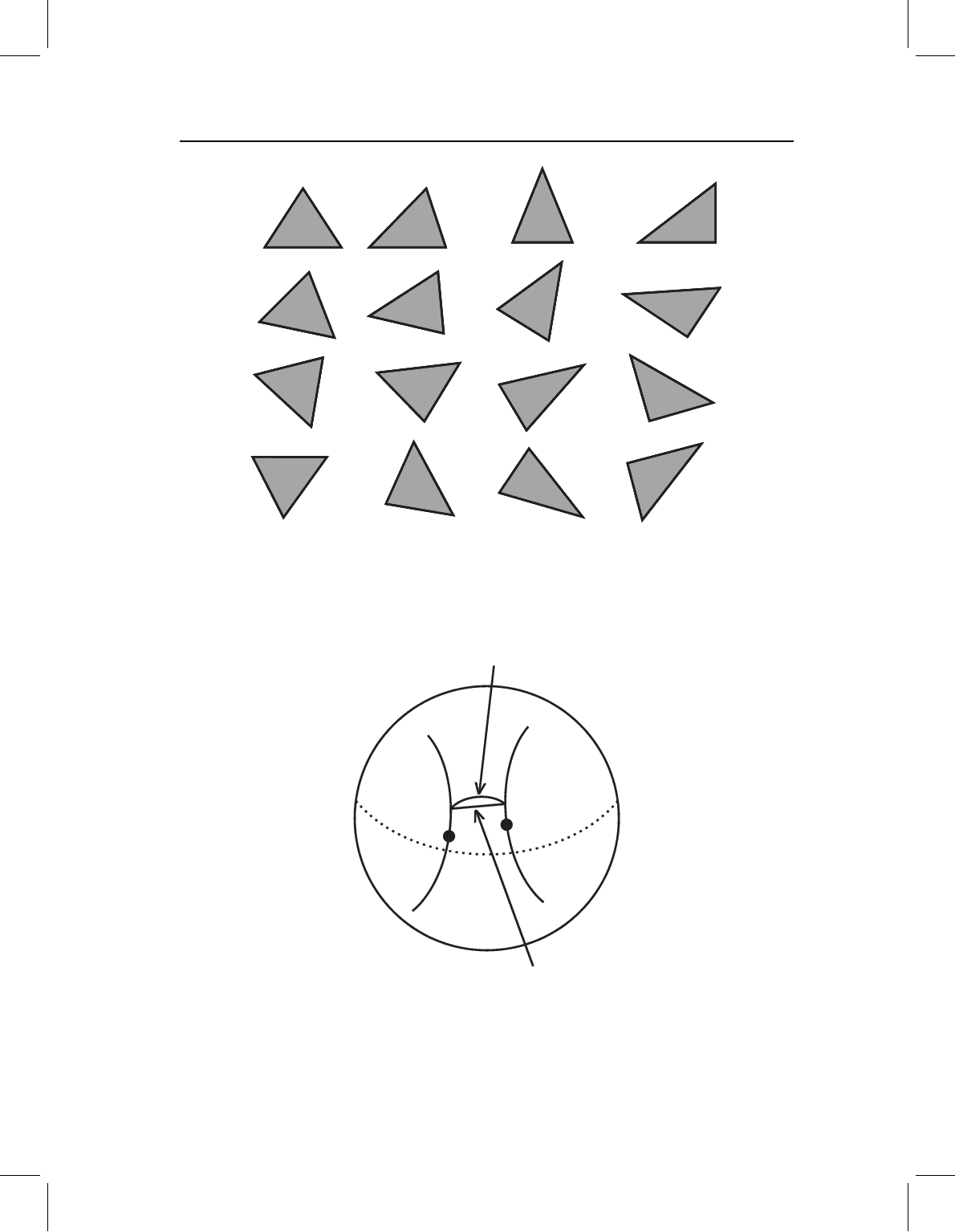
of fibers, we have drawn a cartoon (Figure 4.6) representing four fibers (in columns); the

triangles within a column differ solely by a rotation, whereas those in different columns also

differ in shape. (This visualization is somewhat limited, because a row does not accurately

represent the number of dimensions needed to describe shapes of triangles, as explained

in the next section.)

With the concept of fiber in hand, it is now possible to talk about the separation of

shapes and the distance between them. Figure 4.7 shows the same two fibers on the curved

surface of the pre-shape space hypersphere as in Figure 4.5. In addition, Figure 4.7 shows

an arc (ρ) crossing the surface from one fiber to the other, and the chord (D

) that passes

through the interior of the hypersphere between the same two surface points. We can draw

many such arcs connecting a rotation of the pre-shape Z

with a rotation of the pre-shape

. The arc we want is the shortest one – that is, the one connecting fibers at their “point

of closest approach.” Finding the shortest possible distance between points is a common

tactic for defining distances between objects in spaces. When we find that distance, we

will find the rotation that is optimal in the sense of being the minimum distance between

Figure 4.5 Fibers in pre-shape space. The points Z

and Z

are the locations of pre-shapes on the

hypersphere (centered and scaled matrices computed from two original matrices X

and X

, which

are not shown). Curve 1 passing through Z

is a fiber, the set of all centered and scaled pre-shapes

differing from Z

only by rotation. Curve 2 is a fiber of pre-shapes differing from Z

only by rotation.

(The dotted curve is the “equator” of the hypersphere, and does not represent a fiber.)

chap-04 4/6/2004 17: 22 page 82

82 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

Figure 4.6 An alternative visualization of the concept of a fiber. Each column shows rotations of

a single shape; triangles in different columns differ in shape. Each column represents a single fiber.

Figure 4.7 Determining the distance between the fibers of pre-shapes. The arc ρ is the shortest

distance across the surface of the hypersphere from fiber 1 to fiber 2. The length of the arc is the

Procrustes distance. The length of the chord (D

) is the partial Procrustes distance.

chap-04 4/6/2004 17: 22 page 83

THEORY OF SHAPE 83

Fiber 1

Fiber 2

Figure 4.8 A slice through pre-shape space showing the Procrustes distance (ρ) and the partial

Procrustes distance (D

shapes. The length of this arc is known as the Procrustes distance, and it is quantified by

determining the angle between the radii that connect the center of the hypersphere to the

point at which the fibers most closely approach each other. Figure 4.8 shows the cross-

section through the pre-shape space in the plane defined by those two radii. The angle

subtended by the arc is ρ; the chord length is D

. The length of the arc is equal to ρ (in

radians) times the length of the radius. Because we have constrained the radius to a length

of one, the length of the arc is the value of the angle. This value ranges from zero to π;

at π , the two shapes are on opposite sides of pre-shape space.

Shape spaces

In the previous section, we used the points of closest approach on the pre-shape fibers to

define the distance between two shapes. Now, we use the same criterion to construct a

shape space. This shape space contains one configuration from each fiber, one rotation of a

centered pre-shape. Conventionally, we select a convenient orientation of one pre-shape to

serve as the reference configuration; every other target (or subject) configuration is selected

as the rotation corresponding to the point of closest approach of its pre-shape fiber to the

reference. That is, the orientation is chosen to minimize the Procrustes distance between

the target and reference. The points on those fibers that are farther from the reference differ

from it in both shape and rotational effects. By selecting the point of closest approach, we

reduce each fiber of pre-shapes to a single point (a shape); consequently, configurations in

this set differ only in shape.

The shape space we just described has fewer dimensions than the pre-shape space from

which it was derived. The number of dimensions lost in the transition are given by:

M(M −1)

(4.10)

chap-04 4/6/2004 17: 22 page 84

84 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

where M is the number of landmark coordinates. For two-dimensional landmarks, Equa-

tion 4.10 simplifies to one, which reflects the fact that a planar shape can only be rotated

about its centroid on one axis (the axis perpendicular to the plane of the shape) and still

stay in the same plane. Consequently, shape spaces of two-dimensional configurations of

K landmarks have 2K −4 dimensions. The four lost dimensions are those describing differ-

ences in size (−1), translation (−2) and rotation (−1). For three-dimensional landmarks,

Equation 4.10 simplifies to three, which reflects the fact that a three-dimensional shape can

be rotated about its centroid on three distinct orthogonal axes in the three-dimensional

coordinate space. Subtracting three from the 3K −4 dimensions of the pre-shape space

(from Equation 4.9) yields 3K −7 dimensions for shape spaces of three-dimensional shapes,

which simplifies to five dimensions for the shape space of tetrahedra. The seven lost

dimensions are those describing differences in size (−1), translation (−3) and rotation (−3).

In the special case of triangles, the shape spaces defined above are the familiar two-

dimensional surfaces of three-dimensional spheres. Because this is a reasonably simple

geometry to visualize and illustrate, we will focus on triangles before returning to the

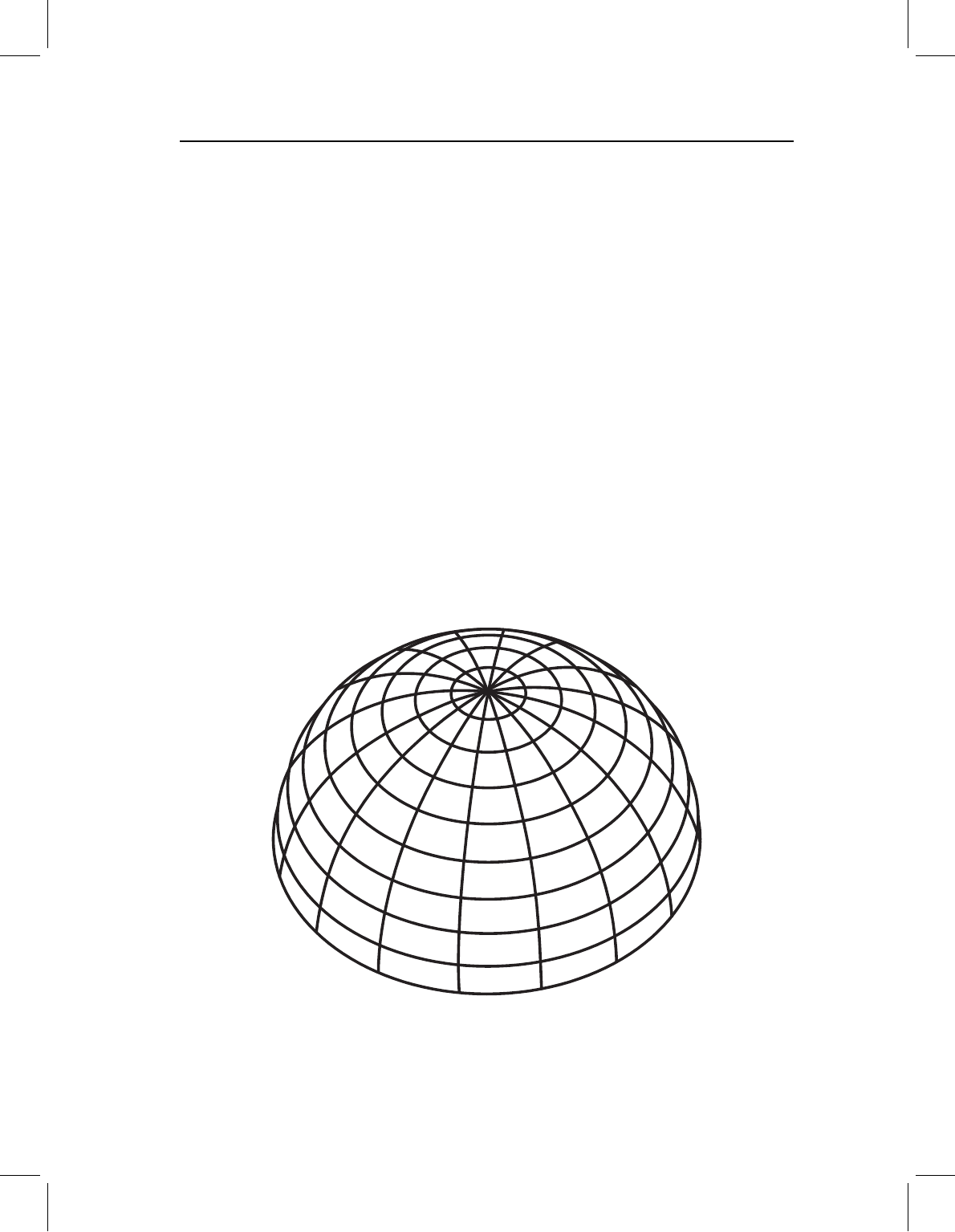
general case. In Figure 4.9 we show half of a space determined by using the equilateral

triangle as the reference. Because we retain the constraints that each triangle is centered

and scaled to centroid size of one, the sphere has a radius of one. For convenience, the

space is oriented so that the point representing the equilateral triangle configuration is

located at the pole. At the equator are triangles with zero height; in other words, various

arrangements of three collinear landmarks. The other half of the space would be an exact

Figure 4.9 Half of the space of triangles that have been centered, scaled to unit centroid size and

aligned with a centered, scaled equilateral triangle. The equilateral triangle is at the pole. Lines of

“latitude” represent shapes equidistant from the equilateral triangle. The “equator” corresponds to

the set of triangles with zero height (three collinear landmarks).

chap-04 4/6/2004 17: 22 page 85

THEORY OF SHAPE 85

reflection of the one shown. Each shape would be a simple reflection of the shape that is

at a corresponding location in the other hemisphere. In the case of triangles, a reflection is

equivalent to a rotation of 180

(albeit on a different axis from the one considered earlier),

so we can discard the bottom half because it contains the same shapes as the top.

Although the shape space just described is a useful construction, it does not satisfy

the mathematician’s urge to find the smallest distances between configurations with those

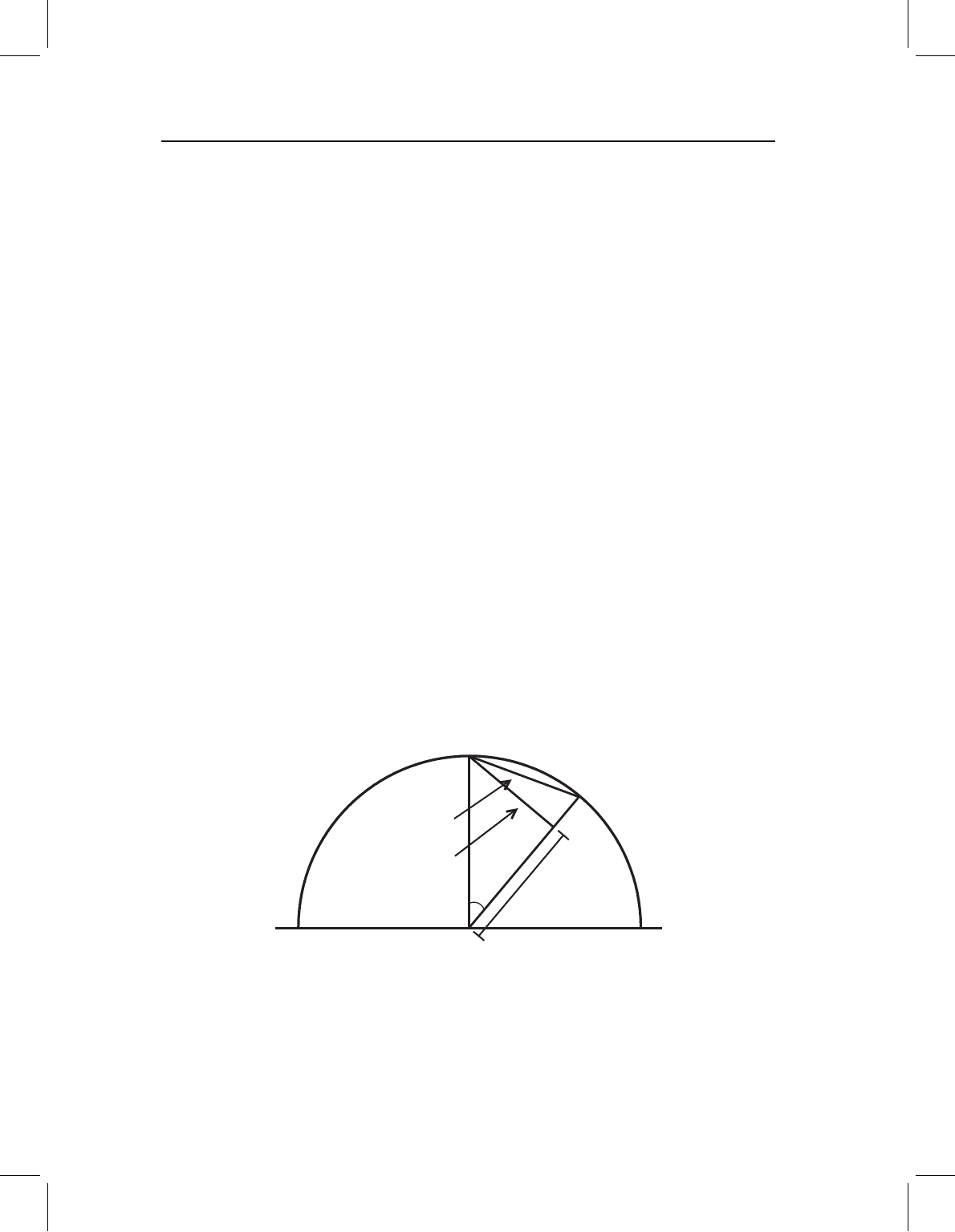
shapes. To illustrate this point, we consider a slice through the polar axis of the hemisphere

of triangles just described (Figure 4.10). As in pre-shape space, the distance of a shape (A)

from the reference is ρ. The angle and the arc length are unchanged because the dimension

eliminated in the transition from pre-shape space to this shape space did not contribute

to the measurement of the shape difference. It should be apparent in Figure 4.10 that the

arc across the surface is not the shortest possible distance between the two shapes. The

chord passing through the interior of the hemisphere would be shorter, but it is still not

the shortest possible distance between configurations with those shapes. We obtain that

shortest possible distance, and the relevant configurations, by changing the constraint on

the centroid sizes of the two configurations. Conventionally, we keep the centroid size

of the reference at one, and allow the centroid size of the target to adopt the value that

minimizes its distance from the reference. This is equivalent to allowing the target to travel

along its radius while the reference stays on the surface. The point along the radius where

the second shape is closest to the target is some distance below the surface of the shape

space, reflecting a reduction of the centroid size of the target. This point (B) is defined

by the line that is perpendicular to the target’s radius and passes through the reference’s

position on the surface. The corresponding centroid size of the target is cos(ρ); the distance

between configurations is sin(ρ) and is called the full Procrustes distance (D

Because cos(ρ) decreases as ρ increases, scaling each configuration in the shape space to

cos(ρ) (where ρ is its distance from the reference) produces a new shape space sphere with a

(0, 1)

(0, 0)

(1, 0)

(⫺1, 0)

cos(r)

Figure 4.10 A slice through part of the space of aligned triangles at unit centroid size, showing the

relationships among the distances between the reference shape (at 0, 1) and A. The semicircle is a

cross-section of the space, which is a hemisphere of radius one. The length of the arc is the Procrustes

distance (ρ), the length of the chord is the partial Procrustes distance (D

), and the shortest possible

distance (obtained by relaxing the constraint on centroid size, producing the configuration B)isthe

full Procrustes distance (D

chap-04 4/6/2004 17: 22 page 86

86 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

(0, 1)

(0, 0)

(1, 0)

(⫺1, 0)

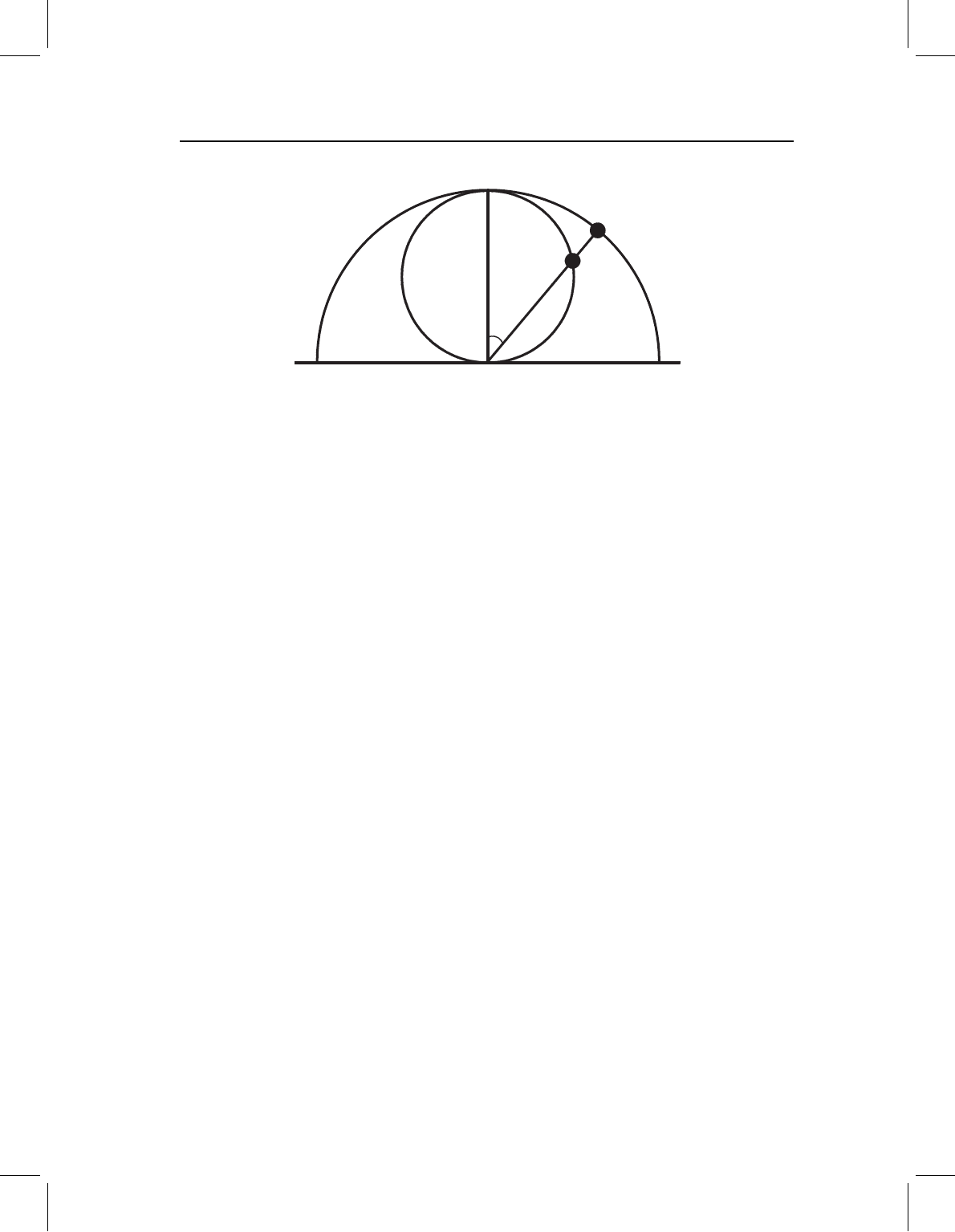
Figure 4.11 The relationship of Kendall’s shape space to the space of aligned triangles scaled to

unit centroid size. The outer semicircle is the cross-section of the space of aligned triangles scaled

to unit centroid size, as in Figure 4.10. The inner circle is a cross-section through Kendall’s shape

space, which is the sphere of aligned triangles scaled to cos(ρ). Kendall’s shape space has a radius of

one-half. Points A and B represent the same shape at CS =1 and CS =cos(ρ), respectively.

radius of 1/2, tangent to the previous shape space at the reference shape (Figure 4.11). This

new space is Kendall’s shape space for triangles; it is the set of centered shapes in which

each is at the size and orientation that minimizes its distance from the reference. It may

appear that Kendall’s shape space is dramatically different from the previous shape space,

but certain key properties remain the same. One of these properties is the distance of the

target shape from the reference shape across the surfaces of the shape spaces. In the first

shape space, the distance of the target from the reference was ρ, the angle subtended by the

arc. In Kendall’s shape space, the angle subtended by the arc is now 2ρ, but the radius is 1/2,

so the arc length is 2ρ/2. Although distances between the reference and the targets are not

altered, distances between targets are (Slice, 2001). Another key property that remains the

same is the number of dimensions. In the transition between shape spaces, the constraint

on centroid size was changed; in Kendall’s shape space the constraint is cos(ρ) instead of

one. This still specifies a single value for each shape; configurations that differ only in size

are represented by a single point in Kendall’s shape space. Thus, Kendall’s shape space for

triangles is also the two-dimensional surface of a three-dimensional sphere.

For configurations of landmarks that are more complex than triangles, we can apply the

same set of operations to move from pre-shape space to the two shape spaces. Regardless of

the number of landmarks and the number of coordinates of those landmarks, the transitions

involve: (1) selecting the rotations that are at the minimum distance from the reference in

pre-shape space, and (2) finding the centroid sizes that fully minimize the distance from

the reference. Describing the geometric relationship of these spaces at higher dimensions is

rather demanding (Small, 1996), but near their poles (i.e. near the reference configurations)

these spaces are expected to have similar properties to the spaces for triangles (Slice, 2001).

Kendall’s shape space and all of the spaces described above are curved, non-Euclidean

spaces. This is important because the conventional tools of statistical inference assume

a linear, Euclidean space. Consequently, we cannot use those tools to analyze shapes in

Kendall’s shape space. Much of Kendall’s own work concerns statistical inference within

chap-04 4/6/2004 17: 22 page 87

THEORY OF SHAPE 87

the curved space that bears his name, but most biologists do not need to work in that space.

As discussed in a later section of this chapter, it is possible to map locations in Kendall’s

shape space to locations in a Euclidean space tangent to Kendall’s shape space. Like planar

maps of the Earth, the Euclidean “maps” of shape space distort the relative positions of

shapes far from the tangent point. This becomes important when comparing extremely

dissimilar shapes. In most biological studies the range of shapes will be small relative to

the curvature of the space, so the distortion will be mathematically trivial for any well-

considered choice of the tangent point (we discuss criteria for selecting the tangent point

in a later section). If you are comparing such highly dissimilar shapes that you need to

work in Kendall’s shape space, you will need a more detailed understanding of this space

than presented here. The excellent texts by Dryden and Mardia (1998) and Small (1996)

discuss the variables and procedures for carrying out inference in Kendall’s shape space.

Finding the angle of rotation that minimizes the Euclidean distance between

two shapes

To determine the angle of rotation required to place one pre-shape at a minimum Procrustes

distance from a second, it is sufficient to rotate the first shape (the target) to minimize the

summed squared distance between it and the reference. This distance we are minimizing

is the partial Procrustes distance. Because the Procrustes distance is a monotonic function

of the partial Procrustes distance, this minimization of the partial Procrustes distance also

minimizes the Procrustes distance.

An arbitrary rotation of the target form (of two-dimensional landmarks, M =2)

by an angle θ maps the paired landmarks (X

, Y

) of the target to the coordinates

((X

cos θ −Y

sin θ), (X

sin θ +Y

sin θ)). The sum of the squared Euclidean distances

between the K landmarks of this rotated target and the reference is:



j=1



−(X

cos θ −Y

sin θ))

+(Y

−(X

sin θ +Y

cos θ))



(4.11)

where (X

, Y

) are the coordinates of the landmark in the reference. To minimize this

squared distance as a function of θ, we take the derivative with respect to θ and set it equal

to zero:

−



j=1



2(X

−(X

cos θ −Y

sin θ))(−X

sin θ −Y

cos θ)

+2(Y

−(X

sin θ +Y

cos θ))(X

cos θ −Y

sin θ)



= 0(4.12)

and solve for θ:

θ = arctangent





j=1

−X



j=1



(4.13)

which gives us the angle by which to rotate the target to minimize its distance from the

reference.