Zelditch M.L. (и др.) Geometric Morphometrics for Biologists: a primer

Подождите немного. Документ загружается.

chap-02 4/6/2004 17: 21 page 48

48 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

Digitizing

This discussion of digitizing explains how to use one particular program, tpsDig.We

recommend using this because all programs for shape analysis can read data in the format

output by this program.

1. Getting ready to digitize your first image

Start the program. Go to the File menu. Select Input source, then File. Find the folder

containing your pictures and select the correct type of files. Select the file you want to

open, or type the file name and extension, and click the Open button. The image should

appear in the main window. In the toolbar above the image are two buttons (+ and −) that

you can use to zoom in or out, and a number that shows the magnification of the image.

Go to the Modes menu, and select Digitize landmarks (if not already checked).

Go to the Options menu, and select Label landmarks (this will put numbers next to the

digitized points). Return to the Options menu, and select Specimen info… In the window

that opens, type a unique specimen identifier in the ID: box. Ignore the other boxes for

now. Click OK. Again, go to the Options menu, and this time select Image tools. In the

window that opens, select the Cursors tab, and choose the digitizing cursor that you prefer.

(You can try out the cursor by moving it over the image. Do not click on the image; if

you do, a landmark will be recorded and the image tools window will close.) Now select

the Colors tab. Here, you can choose the color and size of the circle that will be used to

indicate a landmark’s position, whether the circle will be closed or open, and the color

and size of the number used to label the landmark. You can change these options at any

time. Close this window, and you are now ready to digitize.

Notice that one of the buttons on the toolbar looks like a digitizing cursor. This button

should be depressed, indicating you are in digitizing mode. Also, the cursor will look like

the digitizing cross-hairs, and not your standard mouse pointer. Position the cursor over

the landmark and click the left mouse button. A circle and number should appear. The

# (pound) button on the toolbar is a toggle to hide or reveal the landmark numbers.

2. Editing digitized landmarks

Click the arrow button on the toolbar to enter edit mode, or click the right mouse button.

The cursor will change from the cross-hairs to the arrow. To move a landmark, place the tip

of the arrow on the circle, press and hold the left mouse button, and “drag” the landmark

to the new location. (Note that its number does not change.) To delete a landmark, place

the tip of the arrow on the circle and click the right mouse button. In the pop-up menu,

click on Delete landmark (or select one of the other options if you change your mind).

Note that every landmark with a higher number will be renumbered.

If you click Insert landmark instead of Delete landmark, a point will be inserted to the

left of the selected landmark. The new point will have the number originally assigned to

the selected landmark – the selected landmark and all landmarks with higher numbers will

be renumbered accordingly. Thus, you can use Insert landmark to add skipped landmarks

without redigitizing the entire set. Select the landmark that should be after the skipped land-

mark, right click, choose Insert landmark, and drag the new point to the correct location.

chap-02 4/6/2004 17: 21 page 49

LANDMARKS 49

3. Saving data

After digitizing the specimen, go to the File menu and select Save data. A pop-up window

will open with a space for you to enter a file name. Notice that the default is to save the file

in the same folder as the pictures. Do not change this. Enter the file name with no extension.

It will be saved with a .TPS extension. There is no option here, despite appearances.

You are now ready to digitize a second specimen, but before continuing you should

take a look at the file you have just created. Minimize the tpsDig window, go to Windows

Explorer, find the folder containing your pictures, and open the *.TPS file you just created

(it will probably open in Notepad or Word).

Notice the format of your file (this is the TPS format). The first line is “LM=” followed

by the number of landmarks. The next several lines are X, Y coordinates, in numbers of

pixels. After the coordinates, the next line is “IMAGE=” followed by the name of the

image file. The last line is “ID=” followed by the ID you entered (or a default number that

is a counter). The IMAGE= line does not include the path to the file, only the name. To

see why this is important, close the file and return to tpsDig. Select File, then Input source,

then File. In the pop-up window, select the file you just created and open it. (If you do not

see a list of TPS files, go to the file type box and select TPS files.) tpsDig finds and opens

the image file and displays the landmarks on the image. If you had saved the data file to

a different directory, tpsDig would not be able to find the image file and would refuse to

open the data file.

4. Adding more specimens to the file

To digitize a second image and add the data to the existing data file, open the file containing

the second image and digitize the landmarks, as above. When you are ready to save, go

to the File menu and select Save data. This time, when the pop-up window appears, select

the existing file to which you want to add the new data, and then select Save. In the new

window, select Append. The new data will be added to the end of the selected file.

5. Editing data in a TPS file

Open the TPS file in tpsDig. Use the arrow buttons on the toolbar to scroll through the

images, and edit the digitized landmarks as described above. To save the changes, go to

the File menu and select Save data. This time, when the pop-up window appears, select

the existing file to which you want to add the new data, and then select Save. In the new

window, select Overwrite. This will replace the original data with the modified data, and

landmarks and specimens that were not edited will not be changed. (If you select Append,

you will create a file that has both the original data and the edited data.)

References

Bookstein, F. L. (1991). Morphometric Tools for Landmark Data: Geometry and Biology.

Cambridge University Press.

Bookstein, F. L. (1996). Combining the tools of geometric morphometrics. In Advances in

Morphometrics (L. F. Marcus, M. Corti, A. Loy et al., eds) pp. 131–152. Plenum Press.

Bookstein, F. L., Chernoff, B., Elder, R. et al. (1985). Morphometrics in Evolutionary Biology. The

Academy of Natural Sciences of Philadelphia.

chap-02 4/6/2004 17: 21 page 50

50 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

Fink, W. L. (1993). Revision of the piranha genus Pygocentrus (Teleostei, Characiformes). Copeia,

1993, 665–687.

Oxnard, C. E. (1968). The architecture of the shoulder in some mammals. Journal of Morphology,

126, 249–290.

Roth, V. L. (1993). On three-dimensional morphometrics, and on the identification of landmark

points. In Contributions to Morphometrics (L. F. Marcus, E. Bello and A. García-Valdecasas,

eds), pp. 41–62. Museo Nacional de Ciencias Naturales, Madrid.

Stein, B. R. (1981). Comparative limb myology of two opossums, Didelphis and Chironectes. Journal

of Morphology, 169, 113–140.

Strauss, R. E. and Bookstein, F. L. (1982). The truss – body form reconstructions in morphometrics.

Systematic Zoology, 31, 113–135.

Swiderski, D. L. (1993). Morphological evolution of the scapula in tree squirrels, chipmunks, and

ground squirrels (Sciuridae): an analysis using thin-plate splines. Evolution, 47, 1854–1873.

Taylor, M. E. (1974). The functional anatomy of the forelimb of some African Viverridae

(Carnivora). Journal of Morphology, 143, 307–336.

Zelditch, M. L., Bookstein, F. L. and Lundrigan, B. L. (1992). Ontogeny of integrated skull growth

in the cotton rat Sigmodon fulviventer. Evolution, 46, 1164–1180.

Zelditch, M. L., Bookstein, F. L. and Lundrigan, B. L. (1993). The ontogenetic complexity of

developmental constraints. Journal of Evolutionary Biology, 6, 121–141.

Zelditch, M. L., Sheets, H. D. and Fink, W. L. (2000). Spatiotemporal reorganization of growth

rates in the evolution of ontogeny. Evolution, 54, 1363–1371.

Zelditch, M. L., Sheets, H. D. and Fink, W. L. (2003a). The ontogenetic dynamics of shape disparity.

Paleobiology, 29, 139–156.

Zelditch, M. L., Lundrigan, B. L., Sheets, H. D. and Garland, J. T. (2003b). Do precocial mammals

have a fast developmental rate? A comparison between Sigmodon fulviventer and Mus musculus

domesticus. Journal of Evolutionary Biology, 16, 708–720.

chap-03 4/6/2004 17: 21 page 51

Simple size and shape variables: Bookstein

shape coordinates

This chapter presents a method for obtaining shape variables that is both simple and

visually informative. Called “the two-point registration,” this method produces a set of

shape coordinates, sometimes called “Bookstein shape coordinates,” that can be used

both for graphical displays and formal statistical tests. Bookstein shape coordinates (BC)

provide a useful introduction to shape analysis because they are intuitively accessible, their

formula is relatively straightforward, and understanding them does not require a general

understanding of morphometric theory. We present that theory in Chapter 4, after which

we can introduce alternatives to BC (Chapter 5).

To introduce the two-point registration, we first review the meaning of shape (the

first of several reviews) because this meaning is crucial to the formula. We then focus

on the simplest possible application of the method, the analysis of shapes with only three

landmarks (triangles). We also discuss how information about size can be restored (because

it is removed in the course of the two-point registration). Once we have shape coordinates

and a measure of size, we can then test the hypothesis that two samples of shapes differ

statistically or that shape change is correlated with size change. These statistical tests are

done directly on the coordinates of landmarks – should a statistically significant difference

(or covariance) be found, we can then depict it and describe the variable that differs or

changes. In this chapter we also discuss the description of shape variables and the biological

interpretation of them, because, to a large extent, it is the descriptive power of geometric

morphometrics that makes these methods so useful.

Shape and size revisited

In Chapter 1 we discussed the meanings of shape and size, as they are defined in geometric

morphometrics. We defined shape in terms of operations that do not alter shape – specifi-

cally, translation, rotation and rescaling. These operations can be applied to a simple form,

a triangle, allowing us to obtain a coordinate system. For the triangle shown in Figure 3.1,

we can translate it so that one landmark is at the origin (0, 0) (Figure 3.1A). We can then

ISBN 0–12–77846–08 All rights of reproduction in any form reserved

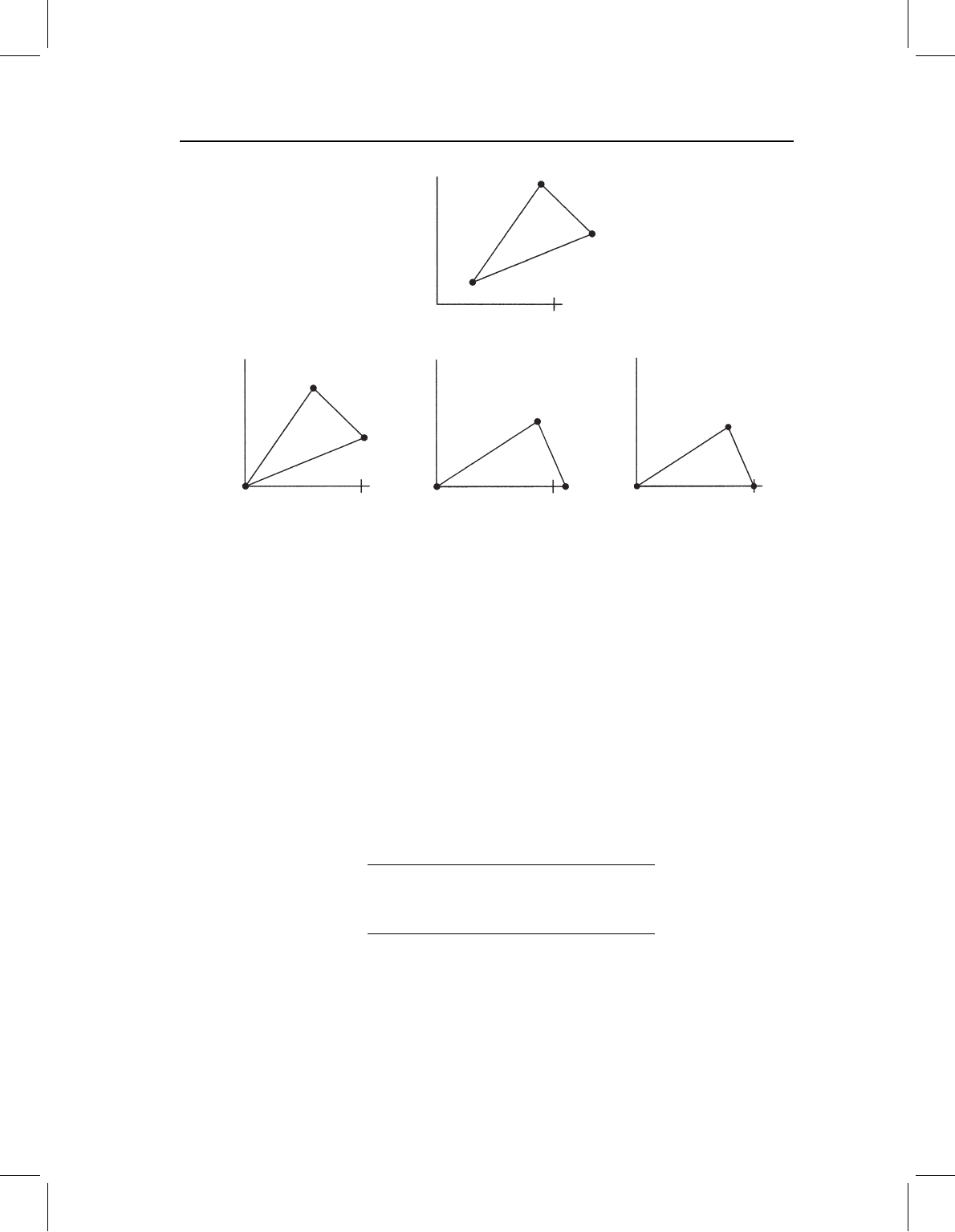
chap-03 4/6/2004 17: 21 page 52

52 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

(A) (B) (C)

Figure 3.1 Three operations that do not alter shape, applied to a triangle: (A) translation;

(B) rotation; (C) rescaling.

rotate it so that the side AB is along the X-axis (Figure 3.1B), and finally we can scale it so

that the coordinate of landmark B is at point (1, 0) (Figure 3.1C). We can then calculate

the coordinate of the third landmark, C, in the coordinate system we have just defined. All

of these operations can be applied without worrying about the consequences for shape,

because we have defined shape such that none of the operations alter it.

Only those three operations are involved in calculating the coordinates of point C, which

is done according to the following formula, in which A

, and C

are the

original digitized coordinates, and SC

, and SC

are the coordinates of landmark C in the

new coordinate system:

−A

)(C

−A

) +(B

−A

)(C

−A

)

−A

)

+(B

−A

)

(3.1)

−A

)(C

−A

) −(B

−A

)(C

−A

)

−A

)

+(B

−A

)

(The numerators for the two equations really do differ in sign, as well as subscripts; that

is not a misprint.)

and SC

are the “shape coordinates” of landmark C (which from now on we

will simply call C

). This relatively simple set of operations will be important when we

compare the shapes of two triangles.

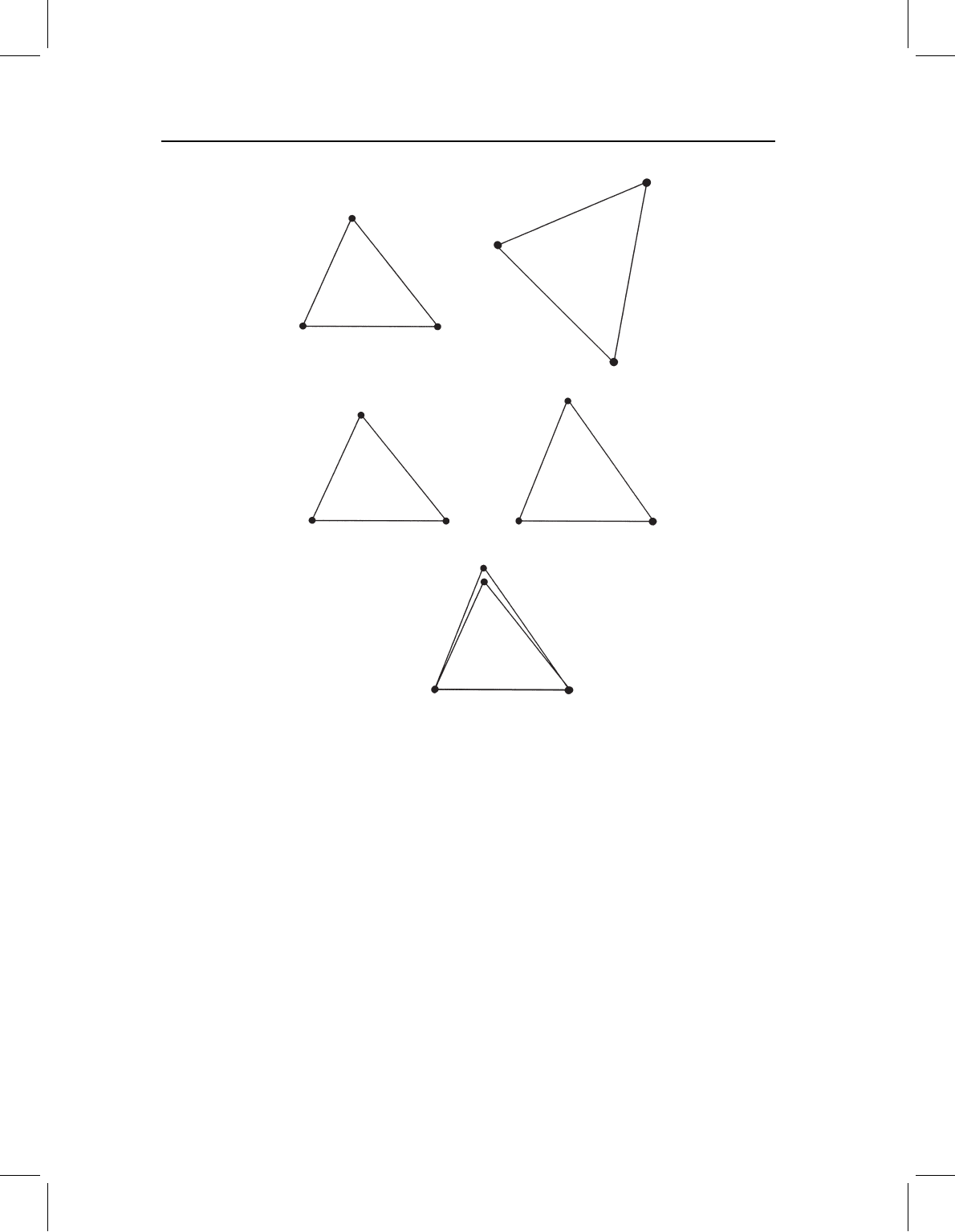
chap-03 4/6/2004 17: 21 page 53

SIMPLE SIZE AND SHAPE VARIABLES: BOOKSTEIN SHAPE COORDINATES 53

(A)

0, 0

1, 0 0, 0 1, 0

0, 0 1, 0

(B)

(C)

Figure 3.2 Two triangles whose shape difference is the subject of investigation: (A) the two triangles

as initially recorded; (B) the same two triangles after being translated, rotated and rescaled by the

two-point registration; (C) the same two triangles, superimposed.

Comparing the shapes of two triangles

Our objective in this section is to answer the question: “do the two triangles of Figure 3.2A

differ in shape?” To do this, we apply the operations outlined above to both triangles and

calculate the shape coordinates of landmark C. That is, we assign the coordinates (0, 0)

to landmark A in both triangles, and we assign the coordinates (1, 0) to landmark B in

both triangles (Figure 3.2B). As a result, the difference between the two triangles is entirely

represented by the difference in the location of the third vertex, landmark C. We can now

draw both triangles on the same coordinate system (Figure 3.2C).

While there are programs to do these calculations, they are easily done in any spreadsheet

or statistical program that manipulates formulae. As an exercise, take the following three

pairs of coordinates for points of a triangle (in the format produced by a common digitizing

program), compute the shape coordinates, and draw the triangle. For the moment, pick

chap-03 4/6/2004 17: 21 page 54

54 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

any two points as the endpoints of the baseline (A and B); we will discuss how to choose

them later.

1. 54.00000 306.00000

2. 223.00000 447.00000

3. 632.00000 300.00000

Now take the next three coordinate pairs, and draw that triangle:

1. 11 342

2. 251 520

3. 769 318

Now draw both triangles using the same baseline (with point A and B superimposed),

and draw the vector extending between the one free (C

) landmark on both of the triangles.

That vector is the shape variable describing the difference between the triangles.

Comparing many triangles

Of course, we rarely (if ever) compare only two specimens (or triangles). We now con-

sider how to compare many individual triangles (below we discuss comparing forms more

complex than triangles). The same procedure (and formulae) still apply, no matter how

many triangles or individuals are examined. For example, given a collection of triangles

(Figure 3.3A), we assign points A and B the coordinates (0, 0) and (1, 0), and then compare

all these triangles (Figure 3.3B) either as whole triangles, or as scatter plots of the one free

point (Figure 3.3C).

The scatter-plot is useful for checking the repeatability of your landmarks, as well as

for studying the variability of shape or differences in shape. For all these purposes, it is

important that the axes of the scatter-plot be sized so that a square shape is shown as a

square – that is, the length of the interval from 0 to 1 on the X-axis should be the same as

the length of the interval from 0 to 1 on the Y-axis. Many programs do not do this scaling

of axes automatically, so you may have to scale the axes yourself. Often this can be done

by first calculating the maximum and minimum values for the X- and Y-coordinates; the

difference between those values, i.e. the range of values should be set equal for both coordi-

nates. For example, if the X-coordinate ranges from 0.030 to 0.060 and the Y-coordinate

ranges from 0.020 to 0.060, both axes should be 0.040 units long (the Y-coordinate has

the slightly larger range). In this case, the minimum on the X-axis could be set to 0.025

and the maximum on the X-axis to 0.065. This distributes the extra length equally above

and below the observed values, and should enforce a 1 : 1 aspect ratio for the graph.

When the axes are on the same scale, an approximately circular scatter of points indi-

cates that there is an equal amount of variation in all directions. Random digitizing error

should be circular; systematic errors, in contrast, will look elliptical. If you have already

digitized landmarks, now would be a good time to compute shape coordinates, scale the

axes appropriately, and check that your digitizing error is circular. Should you find points

that depart substantially from circularity, you should either delete that landmark from

your analysis, or take its biased error into account in subsequent analyses.

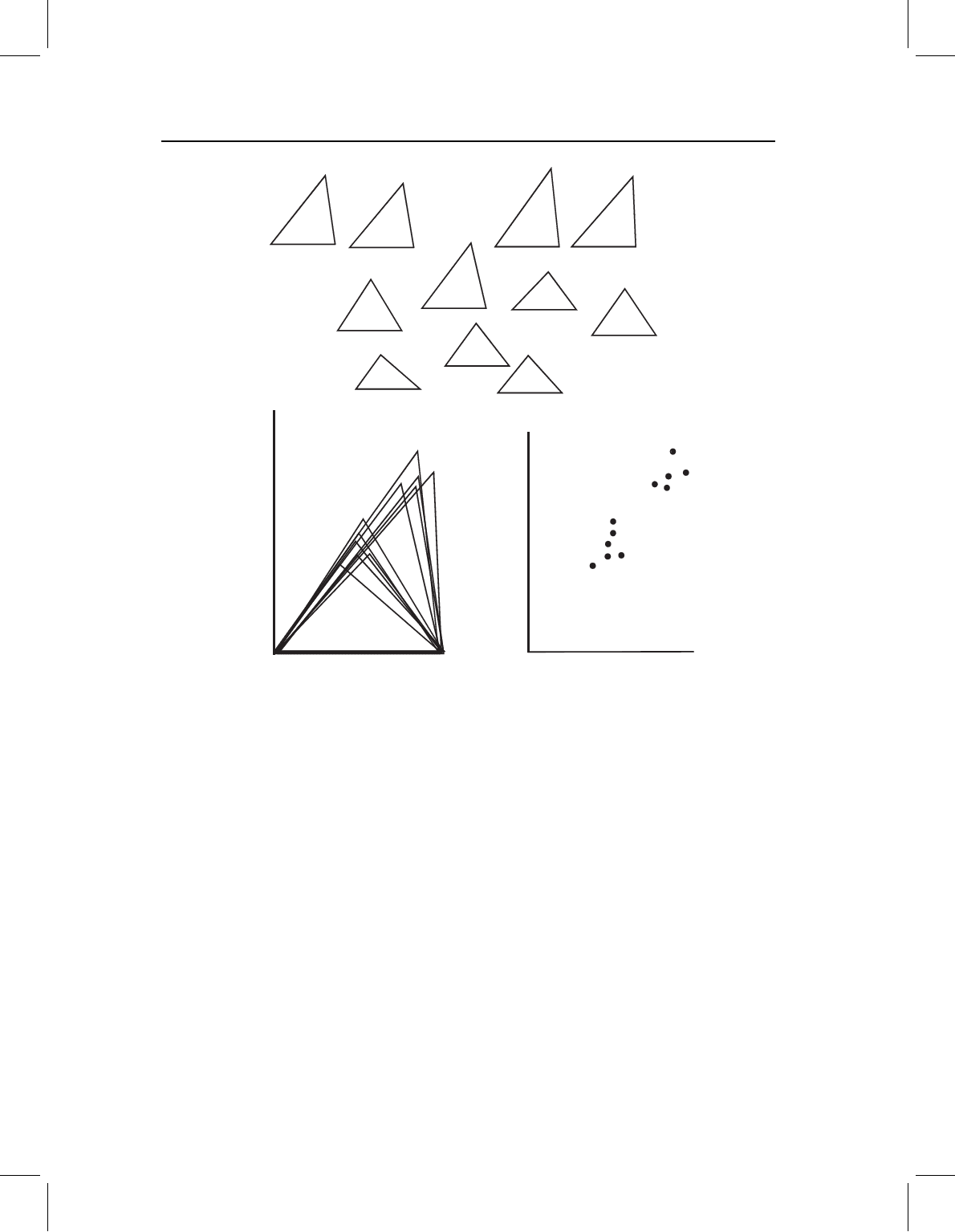
chap-03 4/6/2004 17: 21 page 55

SIMPLE SIZE AND SHAPE VARIABLES: BOOKSTEIN SHAPE COORDINATES 55

0, 0 1, 00, 0 1, 0

(B) (C)

(A)

Figure 3.3 Comparing shapes of triangles: (A) the collection of triangles whose shape differences

are the subject of investigation; (B) the same collection of triangles, put in a common coordinate

system by the two-point registration; (C) scatter-plot depicting the location of the free landmark.

Size

We lost no information about shape when we represented all the triangles by the shape

coordinates of point C, but we did remove information about size. Specifically, we removed

it by rescaling the baseline to a length of one. We can restore the information about size

by using a measure that captures the notion of scale. By scale, we mean the property that

changes when an image is enlarged or reduced. There are several possible meanings of

size, including a simple measure of the length of an organism along one body axis (e.g.

snout–vent length), area, volume, weight or even a linear combination of all measured

quantities that captures the positive correlations among them all (as in the case of the first

principal component). In geometric morphometrics we use a specific concept of size, one

related to geometric scale. One feature of this notion of size is that it is independent of

shape. This is not the case for the other possible size variables mentioned above, which

may be independent of shape but are not necessarily so in all cases. To see this idea of

independence, consider what happens in the case of isometric growth: every dimension

chap-03 4/6/2004 17: 21 page 56

56 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

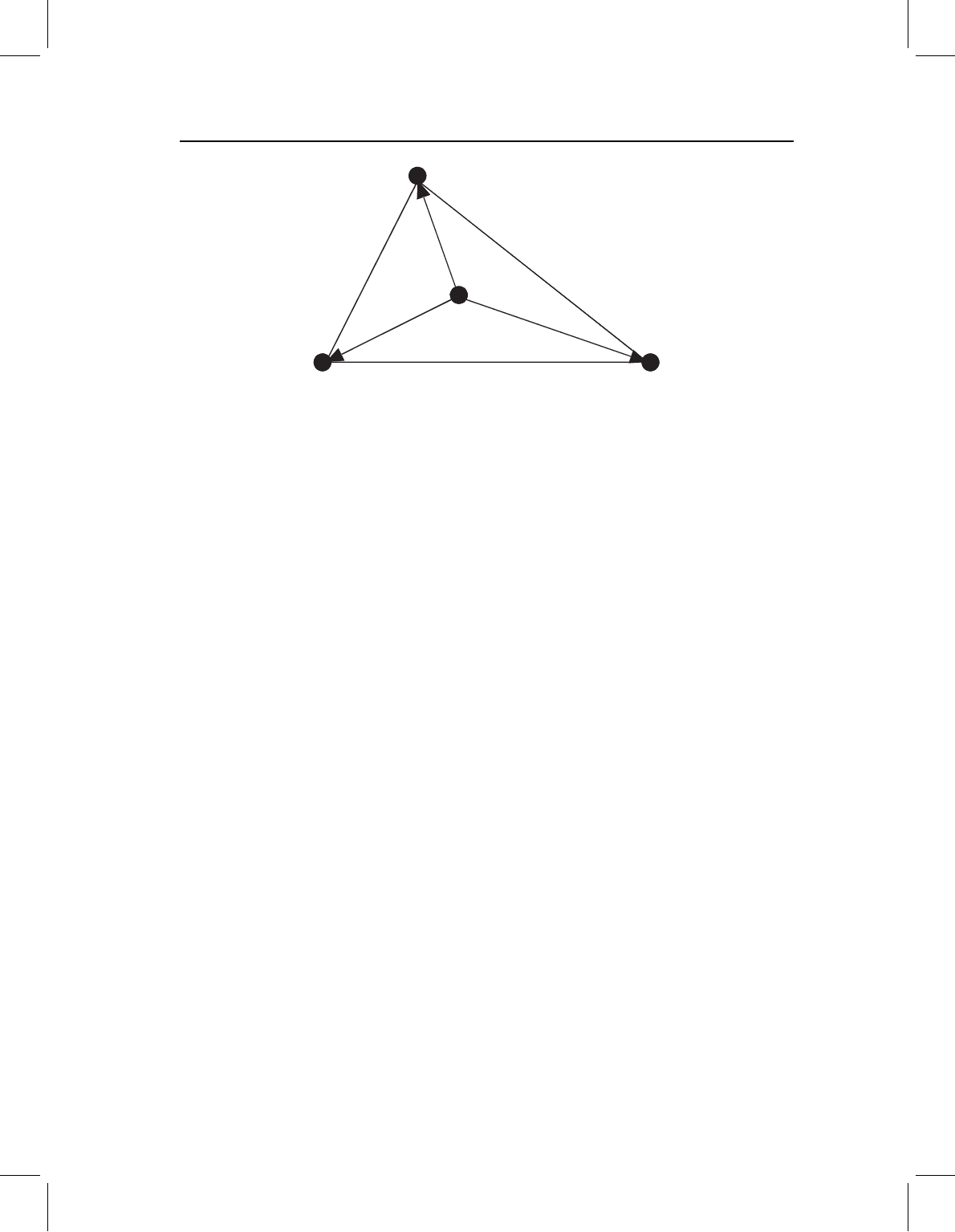
Figure 3.4 A geometric depiction of the calculation of centroid size, which equals the square root

of the summed squared lengths of line segments L1, L2, L3.

is enlarged by the same proportion; each coordinate is moved away from the center in

proportion to its original distance from the center. The size variable that captures this

radial notion of scale is centroid size, graphically illustrated in Figure 3.4.

To compute centroid size, first compute the centroid (center) of the form, which is

located at the mean position of all coordinates. This mean is found by simply averag-

ing the X-coordinates and the Y-coordinates. For example, the three landmarks of the

triangle might be at (0, 0), (1, 0) and (0.3, 0.8). The average X-coordinate is thus the arith-

metic mean of the three X-coordinates (0, 0.3, and 1), which is 0.433, and the average

Y-coordinate is 0.267. Then the squared distance of each of the three landmarks from the

center is calculated using the standard formula for a squared distance between two points

−X

)

+(Y

−Y

)

. This sum gives a measure of size related to area; taking the square

root of the sum gives a linearized measure of size. The square root of the summed squared

distances of each landmark from the center of the form is centroid size.

Size is thus measured separately from shape, and it is statistically uncorrelated with

shape so long as shape changes isometrically (which, by definition, means that shape

does not change with size). This is a useful attribute of a size measure, because we do

not want size to be intrinsically correlated with shape simply by virtue of its formula.

Rather, we want a measure of size that is correlated with shape only when size and shape

change together. Of course real data will often show this correlation between shape and

scale, because allometry is a common phenomenon. However, allometry is an empirical

finding, not an effect of the formula for size. Centroid size is the only size variable that

is uncorrelated with shape in the absence of allometry (others that are also uncorrelated

with shape are variants on centroid size). This independence from shape is one of the main

reasons why centroid size is used as a size variable. The other reason is that centroid size

has a crucial role in defining the metric for a distance between two shapes (Chapter 4).

Choosing the baseline

When we calculated shape coordinates, we chose one side of the triangle to serve as a

baseline. An obvious question is whether our results might depend on that choice. As

Bookstein (1991) has proven, the scatters for different sets of shape coordinates of the

chap-03 4/6/2004 17: 21 page 57

SIMPLE SIZE AND SHAPE VARIABLES: BOOKSTEIN SHAPE COORDINATES 57

same triangle to different baselines differ mainly by translation, rotation and rescaling.

In effect, all the statistical results are (approximately) the same regardless of the choice of

baseline. However, this does not mean the baseline should be chosen arbitrarily. First, some

landmarks are difficult to digitize and may be especially difficult to locate – these should not

serve as an endpoint of the baseline. This is because the method, in effect, transfers all the

variance in the baseline points to all the other landmarks, so if the endpoints of the baseline

are highly variable then all the points will be noisy. More problematically, the variance

is not evenly distributed across all landmarks; the transfer of variance might therefore

introduce a bias into the data. Another consideration that enters into choosing a baseline

is its orientation. If the baseline rotates relative to a body axis it does not compromise

the statistical analyses, but it can make interpretations based on graphics difficult – it

might seem that all the landmarks are moving away from the baseline in the posterodorsal

direction, for example, when the baseline rotates in the anteroventral direction. Also, in

choosing the endpoints of the baseline, we do not want points that are too close to each

other because any highly localized variation in shape may be common to both those points.

Just as the noise of the baseline landmarks is transferred to all the others, the variance local

to the baseline landmarks is transferred to all the other landmarks. Ideally, therefore, we

want endpoints of the baseline to be along the longest diameter of the form that passes

through the centroid of the form, so long as those points are not especially unreliable and

the longest diameter does not rotate.

It is easiest to interpret results when the baseline lies along an organismal body axis.

Even though results can be interpreted in a baseline-invariant way, the interpretations still

refer to sides of the triangle. It is most convenient when at least one side is a conventional

and familiar reference. Bookstein has put a great deal of emphasis on baseline-invariant

interpretations out of a concern for reports free from arbitrary, abiological decisions.

However, organismal body axes are neither arbitrary nor abiological – indeed, we often

want to make explicit references to organismal body axes in our interpretations. Thus,

even though we can interpret shape changes without reference to organismal body axes,

we might still wish to orient our findings with respect to them. This motivates choosing a

baseline along one of those axes.

Statistics of shape coordinates

Once we have shape coordinates, we can answer the basic “existential” questions as defined

in Chapter 1, such as “do these samples differ in shape?” These questions have “yes” and

“no” answers supplied by statistical tests. All conventional statistical methods and tests

can be applied to shape coordinates and centroid size. For example, an average value

for the shape coordinate at point C is computed by averaging the X-coordinates for that

point across all individuals within a sample, then dividing that sum by the total number

of individuals in that sample; the same procedure is then applied to the Y-coordinates.

Variances and standard deviations are also calculated by standard formulae. Because the

two endpoints of the baseline are fixed, they have no variance and should not be included

in statistical analyses. If you use conventional statistical packages to analyze these coordi-

nates, remember to exclude them from the analysis because many programs will not run

if the variables do not vary.