Zelditch M.L. (и др.) Geometric Morphometrics for Biologists: a primer
Подождите немного. Документ загружается.


chap-06 4/6/2004 17: 23 page 138
138 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS
i is the square root of minus one. Complex number notation is often used in texts on the
statistics of shape, so understanding it is useful.
The next idea is to require that the reference form be rotated to a principal axis
alignment, so that
j
X
j
Y
j
=0, which will later simplify the mathematics (but may pose
problems for aligning specimens in some software, discussed below). The summation
j
is from j =1toj =K, and all the summations in the derivation are likewise over all K
landmarks. We are also going to assume that the reference has a centroid size of one, so
that
j
(X
2
j
+Y
2
j
) =1, and a centroid position of (0, 0), so that
j
X
j
=0 and
j
Y
j
=0.
Mathematical derivations Let us consider the two functions of interest: shear, which we
will call S
1
(λ), and compression/dilation, which we will call S
2
(λ)(λ describes the magni-
tude of the mapping). We will be taking the limit as λ →0 at the end of this derivation,
so terms including λ
2
will be discarded. The mappings from a reference form Z to a target
form Z
under these operations are as follows:
S
1
(λ): Z → Z
, Z
=
Z
j
=
X
j
+λY
j
, Y
j
K
j=1
(6.2)
S
2
(λ): Z → Z
, Z
=
Z
j
=
X
j
, Y
j
+λY
j
K
j=1
(6.3)
You can probably convince yourself that S
1
describes a shear; the X-coordinates of each
point are displaced a distance proportional to their Y-axis position relative to the centroid.
Similarly, you should be able to recognize that S
2
describes an expansion of the landmarks
along the Y-axis. We do not need to worry about modeling the contraction along the
X-axis, even though it must also be occurring, because the Procrustes GLS superimposition
will take care of that.
If Z and Z
are both centered (i.e. have a centroid position of zero), then the Procrustes
superimposition may be approximated as the multiplication of Z
by the complex factor
P
Z
, where:
P
Z
=
Z
Z
Z
Z
(6.4)
and the expression
Z
refers to the complex conjugate of the complex vector Z
representing
the landmark configuration after the compression/dilation. The Procrustes superimposition
of Z
on Z is thus P
Z
Z
. To get the vectors that describe the uniform deformation, we just
subtract the starting position Z from P
Z
Z
and then divide through by the magnitude of
the deformation λ, yielding (P
Z
Z
−Z)/λ as the set of vectors describing the deformation.
Further derivation of the uniform components To find P
Z
for the S
2
(λ) mapping
(compression/dilation), we note that the numerator of P
Z
is:
Z
Z
=
j
X
j
+iY
j
×
X
j
−i
Y
j
+λY
j
(6.5)
which expands to:
=
j
X
2
j
−iX
j
Y
j
−iX
j
λY
j
+iX
j
Y
j
−
iY
j
2
−
iY
j
2
λ
(6.6)
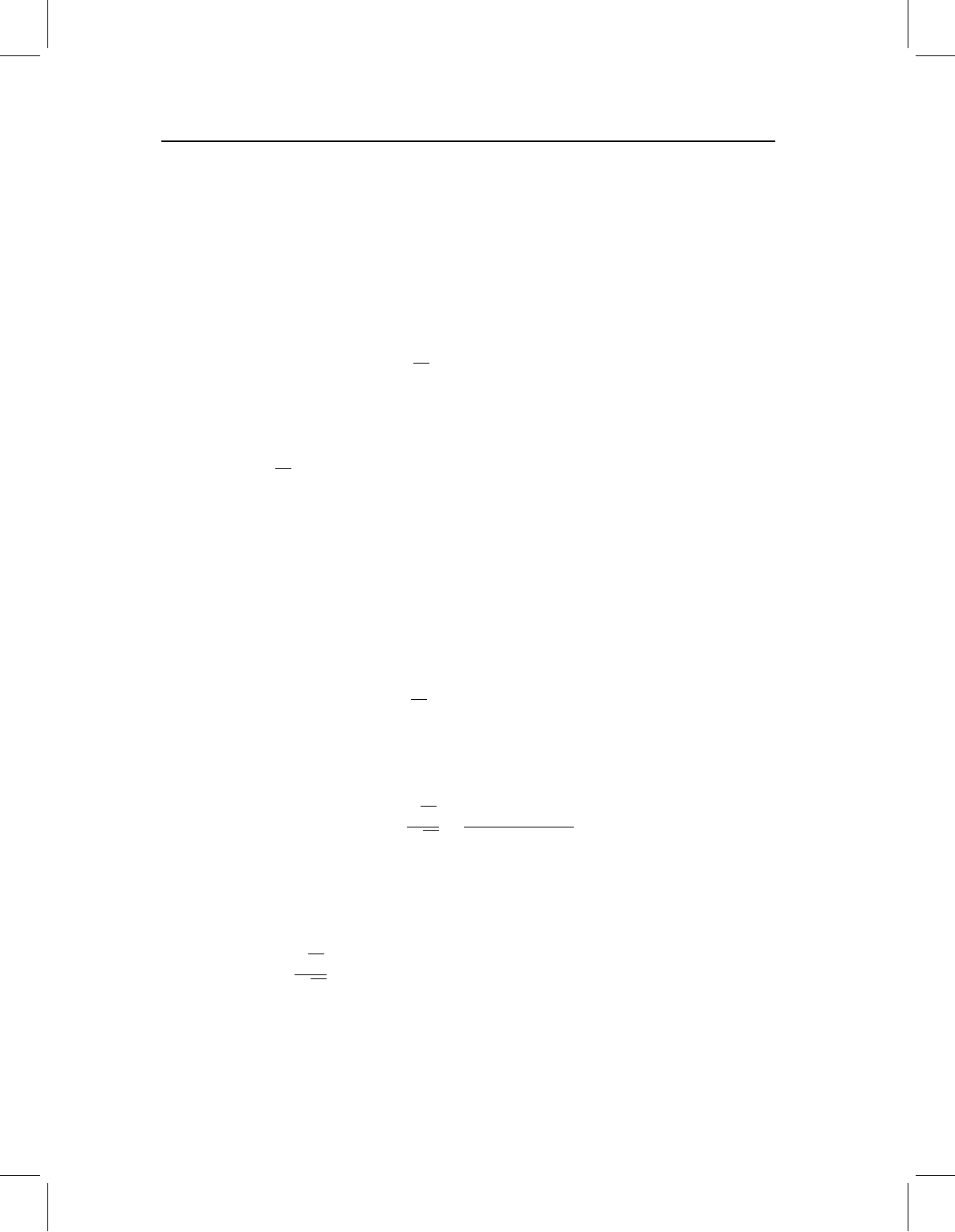
chap-06 4/6/2004 17: 23 page 139
THE THIN-PLATE SPLINE 139
Because i
2
=−1 and the products of X
j
Y
j
sum to zero (under the alignment specified
earlier), we can simplify this to:
=
j
X
2
j
+Y
2
j
+Y
2
j
λ
(6.7)
Now add the constraint that
j
(X
2
j
+Y
2
j
) =1 because we scaled the reference to unit
centroid size, and we have:
Z
Z
= 1 +λ
j
Y
2
j
(6.8)
Now we simplify the denominator of P
Z
:
Z
Z
=
j
X
j
+iY
j
(
1 +λ
)
×
X
j
−iY
j
(1 +λ)
(6.9)
=
j
X
2
j
+Y
2
j
(1 +λ)
2
=
j
X
2
j
+Y
2
j
1 +2λ +λ
2
(6.10)
=
j
X
2
j
+Y
2
j
+2Y
2
j
λ +Y
2
j
λ
2
(6.11)
As mentioned before,
j
(X
2
j
+Y
2
j
) =1, and terms including λ
2
can be discarded in the
limit of small λ, so that:
Z
Z
∼
=
1 +2λ
j
Y
2
j
(6.12)
This leaves us with:
P
Z
=
Z
Z
Z
Z
=
1 +λ
j
Y
2
j
1 +2λ
j
Y
2
j
(6.13)
We can now expand the term 1/(1 + 2λ
j
Y
2
j
)as1−2λ
j
Y
2
j
, keeping only first order
terms in λ for this power series expansion. This gives us:
P
Z
=
Z
Z
Z
Z
∼
=
1 +λ
j
Y
2
j
1 −2λ
j
Y
2
j
∼
=
1 −λ
j
Y
2
j
(6.14)
to first order in λ.
Now we can calculate the landmark coordinates after the operation of the
compression/dilation (S
2
(λ)) and Procrustes superimposition (which is just a multiplication

chap-06 4/6/2004 17: 23 page 140
140 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS
by P
Z
, since Z
is already centered):
P
Z
Z
=
1 −λ
j
Y
2
j
×Z
=
Z
j
=
X
j
1 −λ
j
Y
2
j
,
Y
j
+λY
j
1 −λ
j
Y
2
j
K
j=1
(6.15)
The vector describing the displacement from Z to P
Z
Z
is then:
P
Z
Z
−Z =
X
j
1 −λ
j
Y
2
j
−X
j
,
Y
j
+λY
j
1 −λ
j
Y
2
j
−Y
j
K
j=1
(6.16)
=
−X
j
λ
j
Y
2
j
,
λY
j
−λY
j
j
Y
2
j
−λ
2
Y
j
j
Y
2
j
K
j=1
(6.17)
Noting that λ
2
∼
=
0, we can simplify this to:
=
−X
j
λ
j
Y
2
j
,
λY
j
−λY
j
j
Y
2
j
K
j=1
(6.18)
= λ
X
j
−
j
Y
2
j
, Y
j
1 −
j
Y
2
j
K
j=1
(6.19)
We now define γ =
j
Y
2
j
and α = 1 −
j
Y
2
j
=
j
X
2
j
, so that γ +α =1. After making
these substitutions and dividing through by λ, we have:
V
2
=
P
Z
−Z
λ
=
−γX
j
, αY
j
K
j=1
(6.20)
which is the vector of the displacements at each landmark point (X
j
, Y
j
) produced by the
mapping S
2
per unit of λ. All we need to do now is to normalize this set so that the length
of the vector is one.
The magnitude of this vector is:
j
γ
2
X
2
j
+α
2
Y
2
j
(6.21)
Using the definitions of α and γ to rearrange this and simplify it, we get:
=
γ
2
j
X
2
j
+α
2
j
Y
2
j
=
γ
2
α +α
2
γ =
αγ
(
α +γ
)
=
√
αγ (6.22)

chap-06 4/6/2004 17: 23 page 141
THE THIN-PLATE SPLINE 141
So if we normalize V
2
, we get:
V
2
=
V
2
√
αγ
=
−
γ
√
αγ
X
j
,
α
√
αγ
Y
j
K
j=1
(6.23)
=
−
γ
α
X
j
,
α
γ
Y
j
K
j=1
(6.24)
which is now a unit vector describing a compression/dilation operation followed by
Procrustes superimposition.
Similarly, we start with a shearing operation, S
1
(λ), and corresponding Procrustes super-
imposition, P
Z
, to find the unit vector corresponding to these operations. First we need to
find P
Z
for the S
1
(λ) mapping:
Z
Z
=
j
X
j
+iY
j
×
X
j
+λY
j
−iY
j
(6.25)
=
j
X
2
j
+Y
2
j
+X
j
Y
j
λ +iY
2
j
λ
(6.26)
As before,
j
X
2
j
+Y
2
j
= 1,
j
X
j
Y
j
= 0 and
j
Y
2
j
= γ; therefore:
Z
Z
= 1 +iγλ (6.27)
Also:
Z
Z
=
j
X
j
+λY
j
+iY
j
×
X
j
+λY
j
−iY
j
(6.28)
j
X
j
+λY
j
2
+Y
2
j
=
j
X
2
j
+2λX
j
Y
j
+λ
2
Y
2
j
+Y
2
j
= 1(6.29)
Therefore:
P
Z
=
Z
Z
Z
Z
=
Z
Z
1
= 1 +iγλ (6.30)
Now we can simplify:
V
1
=
P
Z
Z
−Z
λ
=
(1 +iγλ)(X
j
+λY
j
+iY
j
) −(X
j
+iY
j
)
λ
(6.31)
=
X
j
+λY
j
+iY
j
+iγλX
j
+iγλ
2
Y
j
+i
2
γλY
j
−X
j
−iY
j
λ
(6.32)
=
λY
j
+iγλX
j
−γλY
j
λ
= Y
j
+iγX
j
−γY
j
(6.33)
This leads to the series of coordinate pairs:
= (Y
j
(1 −γ), γX
j
)(6.34)

chap-06 4/6/2004 17: 23 page 142
142 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS
or
V
1
= (αY
j
, γX
j
)(6.35)
Dividing this by its magnitude to normalize it yields:
j
α
2
Y
2
j
+γ
2
X
2
j
=
α
2
j
Y
2
j
+γ
2
j
X
2
j
=
α
2
γ +γ
2
α (6.36)
=
αγ
(
α +γ
)
=
√
αγ (6.37)
so the unit vector V
1
is:
V
1
=
αY
j
√
αγ
,
γX
j
√
αγ
K
j=1
=
α
γ
Y
j
,
γ
α
X
j
K
j=1
(6.38)
which may now be used to determine the shear component of the uniform deformation.
Some software packages will give you α and γ as used in the calculation of the uniform
component, others may give you the unit vectors instead. The expressions above (Equations
6.24 and 6.38) are for coordinates of the unit vectors for shear and compression/dilation
for a reference form rotated to principal axis orientation. It turns out to be straightforward
to rotate them to unit vectors to match any reference orientation preferred by a researcher,
although some programs may not offer this option, meaning that the reference may be
oddly oriented by the software.
Calculating uniform components based on other superimpositions
The approach taken in the above derivation was to determine the unit vectors that would
result from a shear or compression/dilation of a reference form, followed by Procrustes
superimposition back onto the reference form. It is also possible to determine the unit
vectors produced by a shear or compression/dilation of a reference, followed by sliding
baseline registration (SBR) or a two-point registration that yields Bookstein coordinates
(BC). These unit vectors and specimens can then be used in SBR or BC to calculate the
uniform components of the deformation, just as we did with those in Procrustes superim-
position. Estimates of the explicit uniform components under SBR are identical to those
derived from the Procrustes-based method presented here. This is not surprising, since the
Procrustes superimposition differs from SBR only in the implicit uniform deformations
(assuming that the Procrustes superimposition, like SBR, is performed with centroid size
set to one, two superimpositions differ only in the rotation and translation terms). Thus,
a deformation displayed by a Procrustes superimposition shows the same change in shape
as the deformation displayed by SBR – the differences between them are due to the implicit
deformations, and do not alter shape. Deformations shown by BC differ from those in
Procrustes superimposition in scale as well as rotation and translation, but these are still
implicit uniform terms. Likewise, RFTRA differs from the other superimpositions only in
the implicit uniform terms.

chap-06 4/6/2004 17: 23 page 143
THE THIN-PLATE SPLINE 143
Decomposing the non-uniform (non-affine) component
The non-uniform part of a deformation differs from the uniform in that it does not leave
the sides of a square parallel. However, like the uniform part, the non-uniform can be
further decomposed into a set of orthogonal components. The decomposition of the non-
uniform deformation is based on the thin-plate spline interpolation function, and produces
components called partial warps. We first describe an intuitive introduction to partial
warps, then a more mathematical one.
An intuitive introduction to partial warps
The non-uniform component describes changes that have a location and spatial extent on
the organism; they are not the same everywhere. They describe spatially graded phenomena
such as anteroposterior growth gradients, and more highly localized changes such as the
elongation of the snout relative to the eye. The notion of spatial scale is central to the
analysis, so we need an intuitive notion of spatial scale. In general (but imprecise) terms,
a change at small spatial scale is one confined to a small region of an organism. To refine
that idea, and develop a firmer grasp of the concept, we show several components at
progressively smaller spatial scales (Figure 6.5).
Figure 6.5A shows a component at large spatial scale that, while broadly distributed,
is not the same everywhere (so it is not uniform). The particular example shown in Figure
6.5A is the elongation of the midbody relative to the more cranial and caudal regions. A
more localized change, confined to the posterior region of the body, is shown in Figure
6.5B – a shortening of the region between the dorsal and adipose fins relative to the dorsal
fin and caudal peduncle. Because more distant landmarks are not involved in the change, it
is more localized than the one shown in Figure 6.5A. Another localized change is shown in
Figure 6.5C, this time confined to the cranial region. This is a shortening of the postorbital
region relative to the regions just anterior and posterior.
The components we have described above and depicted in Figure 6.5 are partial warps,
but to draw them we had to specify their orientation (we drew them as oriented along
the anteroposterior body axis). That orientation is not actually specified by the partial
warps themselves; rather, it is provided by a two-dimensional vector, the partial warp
scores. There is one two-dimensional vector per partial warp. These scores express the
contribution that each partial warp makes to the total deformation. The scores have an X-
and Y-component, and indicate the direction of the partial warp. The idea of direction or
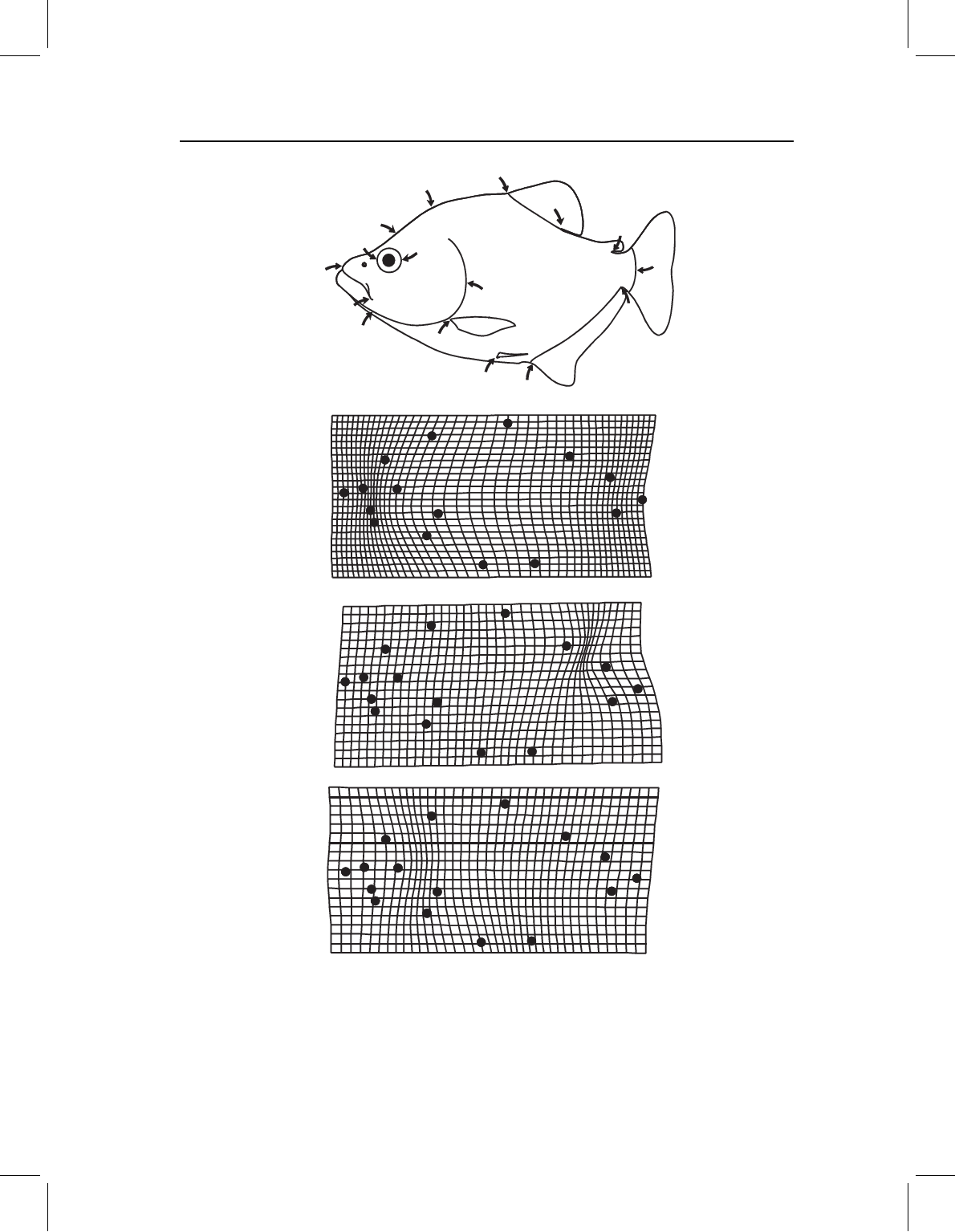
orientation should be familiar from previous chapters. In Figure 6.6 we show one partial
warp (that depicted in Figure 6.5B) multiplied by three different vectors. It may be easiest
to see the directions by looking at the orientation of the vectors at landmarks. Figure
6.6A shows the partial warp oriented horizontally, which in our case corresponds to the
X-direction, so the coefficient of the X-component is large and that of the Y-component
is negligible. In contrast, Figure 6.6B shows the vector with a negligible X-component and
a large Y-component. Figure 6.6C shows the vector with X- and Y-components of equal
magnitudes.
We have described partial warps one at a time, but a complete description (and interpre-
tation) requires combining them all. Taken separately, partial warps are purely geometric
constructs – a function of the location and spacing of the landmarks of the reference form.
They are obtained by a geometric decomposition of the landmarks of the reference form
chap-06 4/6/2004 17: 23 page 144
144 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS
(A)
(B)
(C)
4
9
1
2
3
5
6
7
8
11
12
13
14
15
16
10
Figure 6.5 Three components of the non-uniform deformation, called partial warps. (A) A par-
tial warp at large spatial scale, depicting an expansion of the midbody relative to the head and
caudal body; (B) a partial warp at moderate to small spatial scale, depicting a contraction of the
region between dorsal and adipose fins relative to the length of the dorsal fin and caudal peduncle;
(C) another partial warp at moderate to small spatial scale, depicting a shortening of the postorbital
region relative to the preorbital head and anterior postcranial body.
chap-06 4/6/2004 17: 23 page 145
THE THIN-PLATE SPLINE 145
3
4
9
1
2
5
6
7
8
11
12
13
14
15
16
10
(A)
(B)
(
C
)
Figure 6.6 One partial warp, oriented in three directions: (A) along the X-axis; (B) along the Y-axis;
(C) equally along X- and Y-axes. Due to the orientation of our landmark coordinates, the X-direction
corresponds to the anteroposterior axis, and the Y-direction corresponds to the dorsoventral axis.
To make it easier to see the direction in which the partial warps are oriented, we also display them
by vectors of relative landmark displacements.

chap-06 4/6/2004 17: 23 page 146
146 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS
(as explained in detail in the next section). Although they provide a basis for the tangent
space, they cannot be interpreted except in these abstract terms – we cannot, for example,
say that one part of the change in the ontogeny of the fish is a shortening of the region
between dorsal and adipose fins relative to the dorsal fin and caudal peduncle. That is
a component of the deformation, not a component of an ontogeny. Only by looking at
the total deformation can we say where change occurs. We have discussed them sepa-
rately only to explain what they are (none of the currently available software draws them
separately – to produce Figures 6.5 and 6.6 we had to use specialized software).
To summarize our intuitive presentation of spatial scale, we repeat our major points.
First, any non-uniform deformation can be decomposed into a series of components (par-
tial warps) at progressively smaller spatial scales. Each component describes a pattern of
relative landmark displacements, based on the spacing and location of landmarks in the
reference form. Each partial warp is multiplied by a two-dimensional vector (the partial
warp scores) that measures the contribution made by the partial warp (in each direction)
to the total deformation. We now present a more technical introduction to the thin-plate
spline.
An algebraic introduction to partial warps
Algebraically, partial warps are obtained by eigenanalysis of the bending energy matrix.
Eigenanalysis may be familiar from a quite different context, for example, principal com-
ponents analysis, where it is used to extract eigenvectors (PCs) of the variance–covariance
matrix of measurements. The exact same mathematics is involved in calculating the partial
warps; the difference lies in the matrix being analyzed. Rather than extracting eigenvectors
of a variance–covariance matrix, we instead extract them from the bending-energy matrix.
(We will discuss eigenanalysis further in Chapter 7; here we focus on the derivation of the
bending energy matrix.)
The idea behind the thin-plate spline is that it will approximate the observed deformation
by a linear combination of a function that is the smoothest available and that fully describes
the observed deformation. The function satisfying that pair of requirements has the form:
Z(X, Y) = U(R) =−R
2
ln R
2
(6.39)
where R is the distance between a pair of landmarks in the reference configuration (scaled
to unit centroid size). This particular function satisfies the biharmonic equation:
2
U =
d
2
dx
2
+
d
2
dy
2
2
U(R) ∝ δ
(
0,0
)
(6.40)
where δ
(0,0)
is the generalized function, or delta function, which is defined to be zero
everywhere except at X =0, Y =0, with the odd requirement that:
δ
(
0,0
)
dx dy
= 1(6.41)
The delta function is oddly behaved, but mathematically tremendously useful. It is
sometimes called a functional, rather than a function.

chap-06 4/6/2004 17: 23 page 147
THE THIN-PLATE SPLINE 147
U is said to be the fundamental solution of the biharmonic equation, which is the
equation for the shape of a thin steel plate lifted to a height Z(X, Y) above the (X, Y)-plane.
This is because the bending energy (BE) of the steel plate at a point (X, Y) is given by:
d
2
U
dx
2
2
+2
d
2
U
dx dy
2
+
d
2
U
dy
2
= BE(X, Y)(6.42)
and the total bending energy of the entire plate is:
BE
(
X, Y
)
dx dy
(6.43)
which is the bending energy at each point integrated over the entire surface. The choice of
U(R) minimizes this total bending energy.
For biological purposes, we do not really care about the bending energy of a steel plate.
Rather, we care about the connection between bending energy and the curvature of the
plate (and their connection to spatial scale). Minimizing bending energy minimizes the
curvature of the plate, so when we fit a linear combination of the U(R) function to our
data, we are fitting a function that minimizes the amount of curvature needed to model
the observed deformations.
Suppose we want a linear combination of U(R) values, centered on each of the K land-
marks of our reference form (because we are describing a deformation, we are talking
about changes relative to a reference). We need to describe deformations in the X and Y
directions, so we form the following linear combinations:
f
X
(
X, Y
)
= A
X1
+A
XX
X +A
XY
Y +
K
i=1
W
Xi
U(X −X
i
, Y − Y
i
)(6.44)
f
Y
(
X, Y
)
= A
Y1
+A
YX
X +A
YY
Y +
K
i=1
W
Yi
U(X −X
i
, Y − Y
i
)(6.45)
where f
X
(X, Y) and f
Y
(X, Y) are the spline functions that describe the deformations along
the X- and Y-directions relative to the reference form, and W
Xi
and W
Yi
are weights
of the functions U(X −X
i
, Y −Y
i
), centered on the landmark locations of the reference
(X
i
, Y
i
). The A terms describe uniform (or affine) deformations of the target, using what
is known as the six-component uniform model. We need to include those A terms at this
stage, but will discard them later in favor of the two uniform components discussed earlier
(Equations 6.24 and 6.38).
Fitting the functions to the observed deformations is a standard problem in systems of
linear equations; we can thus cast the problem into matrix form. We form a (K +3) ×2
matrix V of the observed deformations at each of the K landmarks, where the deformation
