Zelditch M.L. (и др.) Geometric Morphometrics for Biologists: a primer

Подождите немного. Документ загружается.

chap-07 4/6/2004 17: 24 page 168

168 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

0.0000

0.0002

0.0004

0.0006

0.0008

0.0010

0.0012

0102030

Ordinal number of principal component

Eigenvalue

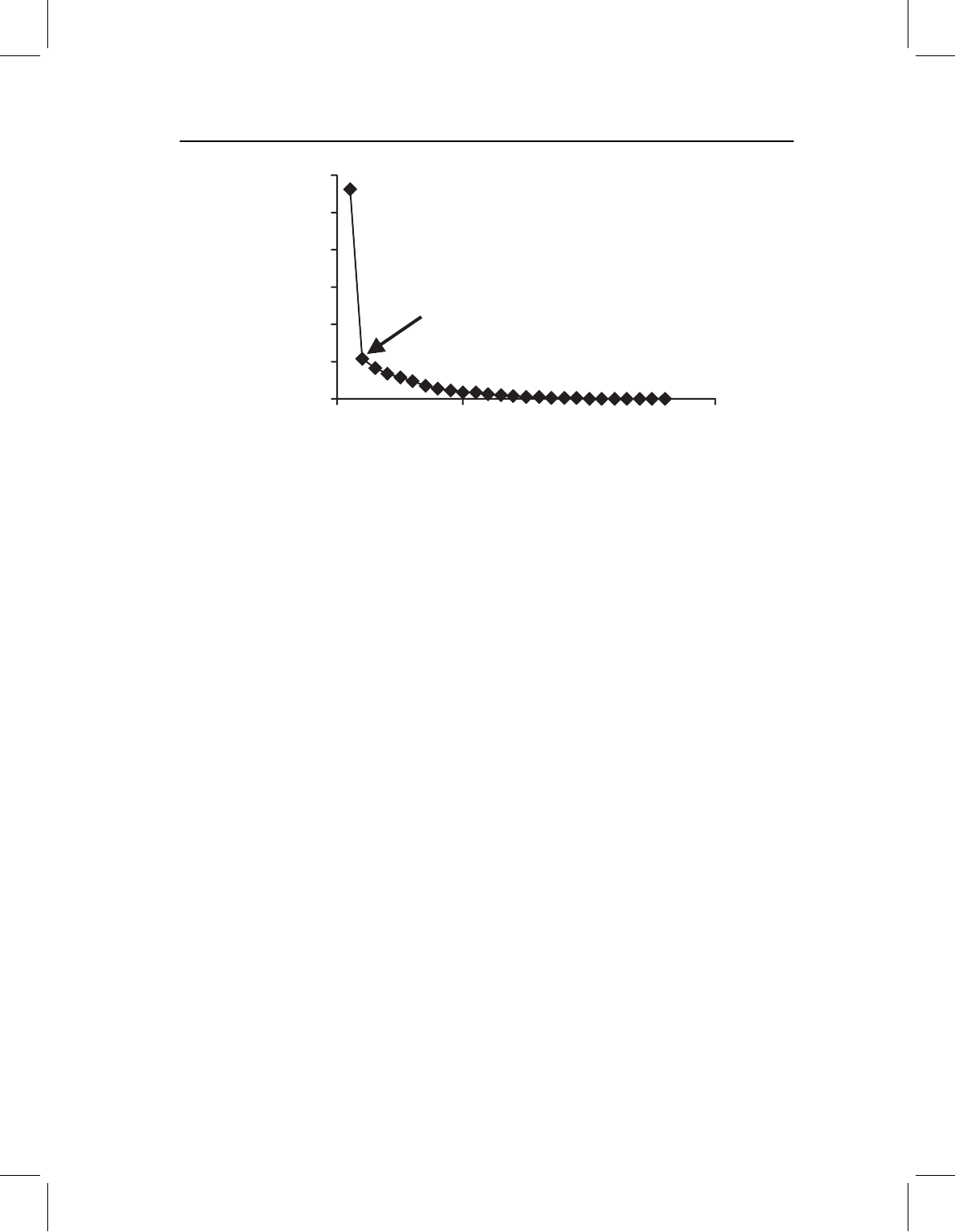
Figure 7.7 Scree plot of the proportion of variance described by each PC for the squirrel jaw data

set. Arrow indicates the inflection point.

they describe anything biologically meaningful. One common rule of thumb is to interpret

only those components that represent more than 5% of the variance. In the squirrel jaw

example, PCs 1 through 5 meet this criterion. They account for a total of 80.4% of the

variance in the sample, leaving 19.6% undescribed. This may seem like a large proportion

of the variance to omit from further analysis, but it is doubtful that any one of the remaining

21 components describes a meaningful amount of variance.

The similarity in magnitudes of variances described by most components can be seen in

a scree plot, in which the variance, or percentage of the total variance, is plotted against the

ordinal number of the PCs (Figure 7.7). In this example, there is a large difference between

the variances of the first two PCs, and much smaller differences between successive pairs

of components. This difference is reflected in the scatter plot of scores in the two axes

(Figure 7.8); the range of scores is much larger on PC1 than PC2, indicating that PC1

accounts for a much larger portion of the total variance. If two components have similar

variances (e.g. if the distribution of scores in Figure 7.8 were closer to circular), then we

have grounds to question whether either of them can be attributed to a distinct causal

factor. Thus, an alternative rule of thumb is to find the inflection point on the scree plot

and interpret only those components to the left of the inflection point (where the variance

of each component is distinct from the variance of the following component). The main

difficulty with applying this rule is that scree plots often do not have inflection points that

are as obvious as the one in Figure 7.7.

Fortunately, there is a more rigorous approach to testing whether two successive PCs

have distinct variances. This is an application of a test developed by Anderson (1958)

and discussed in Morrison (1990). The null hypothesis is that some set of R consecutive

eigenvalues are equal to each other. In other words, the variation described by these com-

ponents cannot be distinguished from random variation. The eigenvalues are numbered

from Q +1toQ +R, where Q is a function of P (the total number of eigenvalues) and

R (the number of the particular components of interest) such that Q =P −R. Anderson

(1958) derived a χ

statistic based on the likelihood-ratio criterion to test the hypothesis

chap-07 4/6/2004 17: 24 page 169

ORDINATION METHODS 169

⫺0.02

⫺0.04

⫺0.08 ⫺0.06 ⫺0.04 ⫺0.02

0.00

0.02

0.04

0.00 0.02

PC1

PC2

Figure 7.8 Scatter plot showing scores on the first two PCs for the sample of 31 squirrel jaws shown

in Figure 7.6.

that the Q +1 eigenvalue is not distinct from the higher numbered eigenvalues:

=−N



j=Q+1

ln λ

+NR ln





j=Q+1



(7.36)

where N is the sample size minus one. When N is large, the degrees for freedom are

(½ R(R +1) −1) (d.f. =2 when R =2). In the special case where Q +R =P, the test eval-

uates whether variation in the last R eigenvectors is spherical. To test two successive

eigenvalues, R is set to 2. For the squirrel jaw example, comparison of the first two eigenval-

ues yields χ

=19.12, which has a p-value less than 0.0001. Comparison of the second and

third eigenvalues yields χ

=0.55, which has a p-value of 0.76. Thus, PC1 is the only one

with a distinct eigenvalue, and the only one that can be regarded as biologically meaningful.

If you use several software packages to run PCAs, you may occasionally find the results

differ in signs for the PCs (when that happens, the scores for individuals on those axes also

differ by a sign). Reversed axes and scores can be disconcerting, but there is no need to

worry – the sign of a PC is arbitrary. If A

is an eigenvector corresponding to λ

, then so is

−A

. If we change the sign on A

, then the score of the jth specimen on the first axis will

also change sign; Y

so the product Y

does not change sign. In other words,

the eigenvectors A

and −A

are simply mirror images. The choice of sign has no effect on

the interpretations of this component, and no effect on the computation of the subsequent

component (a vector orthogonal to A

will also be orthogonal to −A

To this point we have not discussed how to interpret the pattern of variation represented

by a PC. That rests on the coefficients of the PC, which express the relationship between

the PC and the original variables. Because our original variables are shape variables, we

can generate a picture of shape variation along any PC by multiplying the original shape

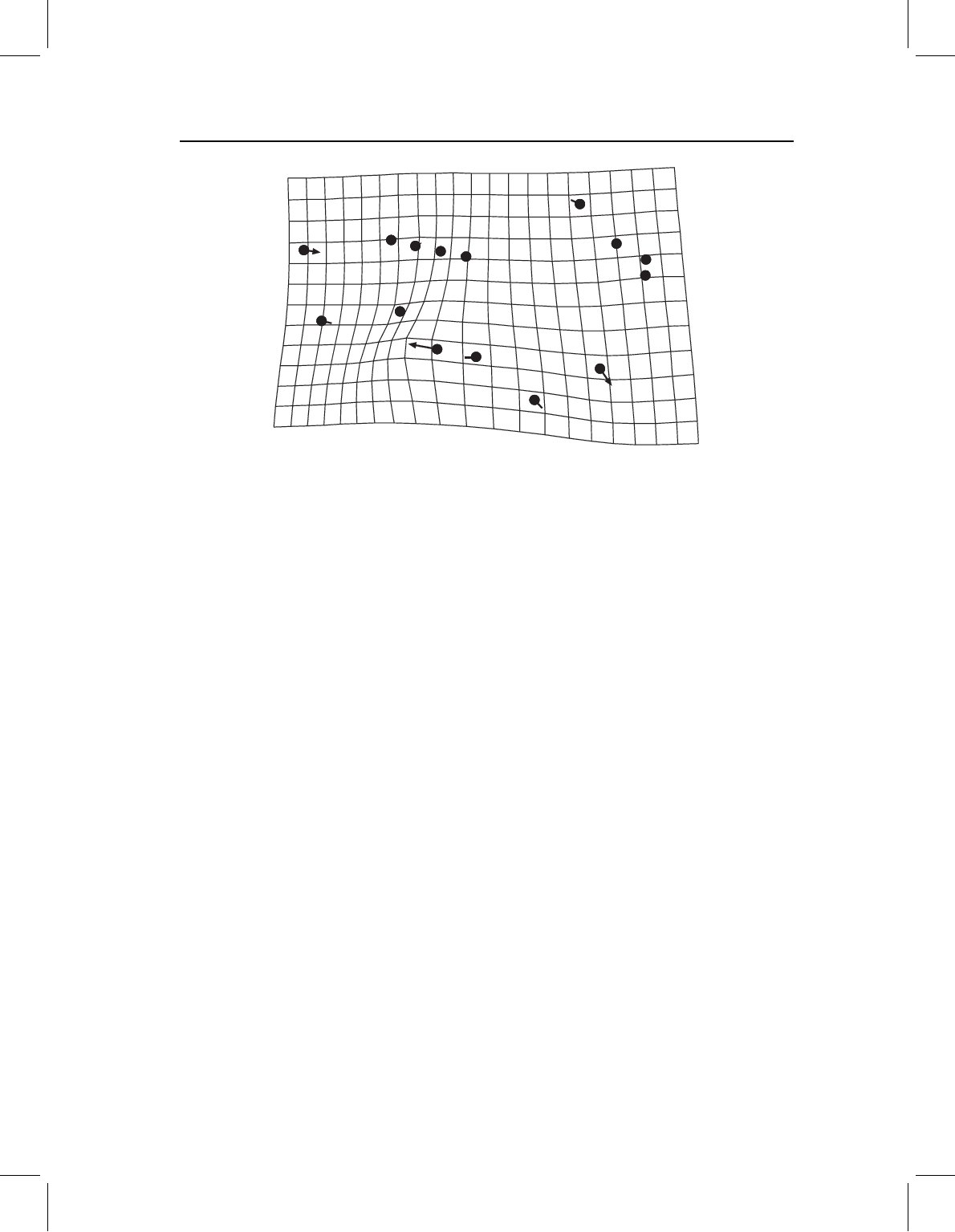
variables by the coefficients of the PC and summing them. Figure 7.9 shows the result of

that computation for PC1 of shape variation in the sample of squirrel jaws.

chap-07 4/6/2004 17: 24 page 170

170 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

Figure 7.9 Pattern of shape change along PC1 for the 31 squirrel jaws shown in Figure 7.6. Circles

indicate the locations of the landmarks in the mean shape of the sample; arrows indicate the changes

in the relative positions of the landmarks as the score on PC1 increases. The deformed grid illustrates

the thin-plate spline interpolation over the entire form.

We should note that many of the studies applying PCA to geometric data call the method

“relative warps analysis” (RWA). PCA and RWA are not exactly equivalent, because the

components of variance extracted by RWA are sometimes weighted by bending energy

(originally, RWA was an analysis of components of variation relative to bending energy,

hence the term “relative” in the name of the method). When variation is not weighted by

bending energy, RWA is PCA. We prefer the more familiar term.

Canonical variates analysis

The purpose of CVA is to simplify the description of differences among groups. For exam-

ple, CVA could be used to describe differences in mandible shape among queens, soldiers

and workers in a colony of ants. It could also be used to describe differences in soldier mor-

phology among colonies, species, or more inclusive categories. If individuals in a study can

be sorted into mutually exclusive sets, CVA can be used to describe the differences among

those sets. However, again we caution that CVA cannot be used to test the statistical signif-

icance of the differences among sets; for that, multivariate analysis of variance is needed.

There are many similarities between CVA and PCA. Like PCA, CVA constructs a new

coordinate system (the canonical variates, CVs) and determines the scores on those axes

for all individuals in a study. Also, the CVs are linear combinations of the original variables

and are constrained to be mutually orthogonal. However, whereas PCA is used to describe

differences among individuals, CVA is used to describe differences among group means.

In this sense, CVA is analogous to a PCA of the group means. Another difference between

CVA and PCA is that CVA uses the patterns of within-group variation to scale the axes

of the new coordinate system. Because of this rescaling, CVs are not simply rotations of

the original coordinate system, and distances in CV space are not equal to distances in the

original coordinate system. (This is where the analogy breaks down.) Although rescaling

chap-07 4/6/2004 17: 24 page 171

ORDINATION METHODS 171

may complicate interpretations of CVs, it also adds to their utility. As a result of the

rescaling, CV1 is the direction in which groups are most effectively discriminated, which

is not necessarily the direction in which the group means are most different.

Groups and grouping variables

A group is a set of individuals that share a particular state of a discontinuous trait. Exam-

ples of groups include sexes, color morphs, species, and supraspecific categories like guilds.

To be analyzed by CVA the groups must be mutually exclusive, meaning that they cannot

comprise nested or intersecting sets. The groups differ by a categorical variable, which is

sometimes called a “qualitative trait” or a “grouping variable.” The important character-

istic of these variables is that they are not measured nor arrayed in a sequence; they do not

have intrinsic numerical values, and nor do they have an inherent order or sequence.

Sometimes, features that can be scored on a continuous graded scale are treated as cate-

gorical variables. For example, the proportions of meat and vegetation in an animal’s diet

can be quantified and scored along a continuum. Nevertheless, it is a common practice to

sort diets into a small number of categories (e.g. carnivore, herbivore, omnivore). Other

traits that might be treated in a similar fashion include geographic location and age. There

are several reasons for treating these kinds of traits as categorical variables. One is a lack

of sufficient information to justify or support a more finely graded analysis – for example,

a researcher may not have precise data on the proportions of food items in the diets of

all species or individuals in a study. Another reason for treating a quantifiable trait as a

categorical variable is that the investigator may not want to impose a hypothesis of order-

ing on the data, which is often a consideration when groups are not dispersed along a

single straight line. Similarly, the investigator may not want to assume that all steps are of

equal value (e.g. ontogenies often can be divided into discrete instars or age classes based on

sequences of developmental events, but the sequentially numbered steps may represent dif-

ferent amounts of time or ontogenetic change). Under these circumstances, a quantifiable

trait can be treated as a categorical variable and CVA would then be used to describe differ-

ences among the groups delineated by distinct states. However, the user should be aware

that taking this approach also limits the inferences that can be drawn from the result – for

example, an observation that age classes can be differentiated does not necessarily imply

the kind of monotonic progression from age to age that can be inferred from a regression.

Geometric description of CVA

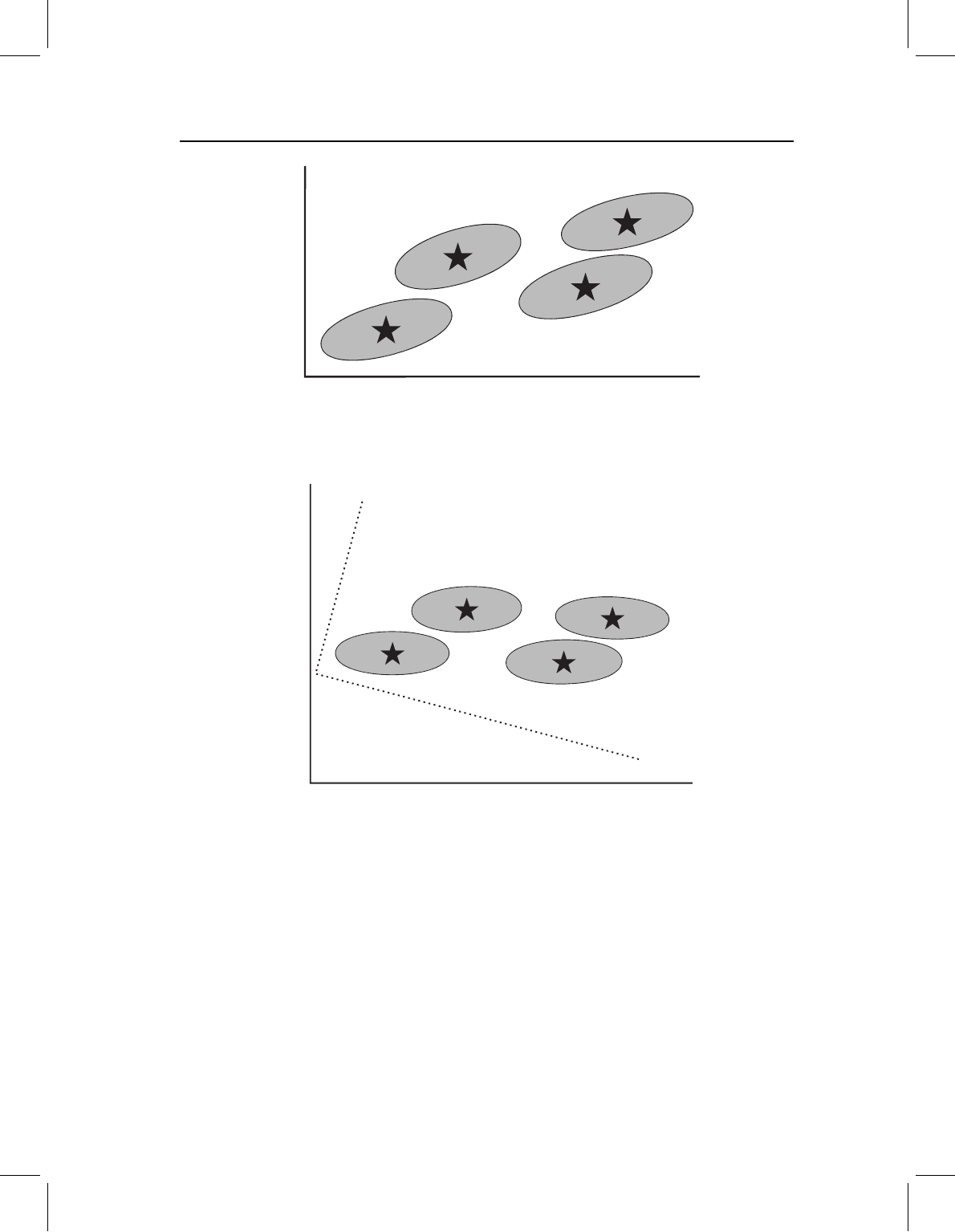
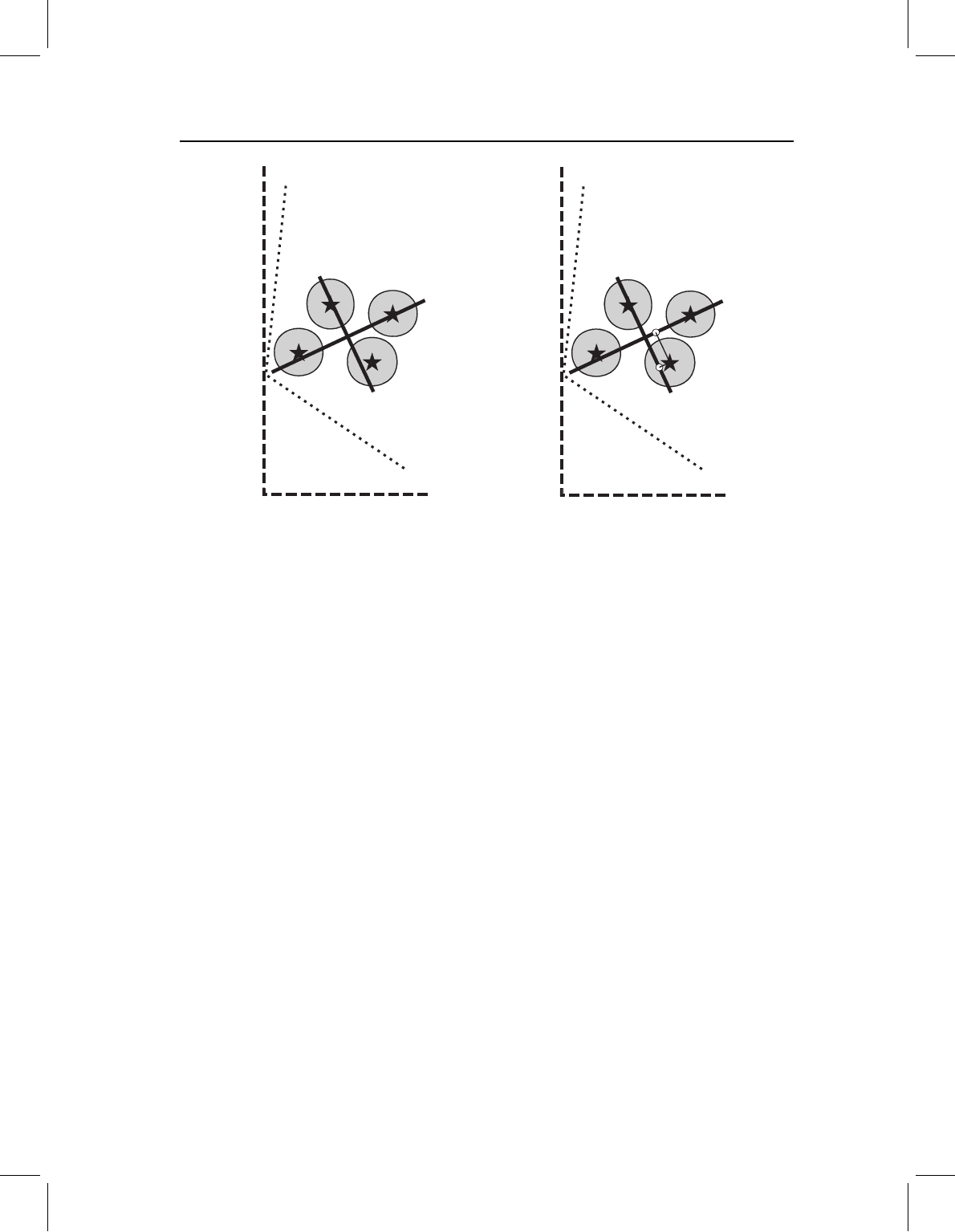
To develop a geometric intuition for CVA, we return to the metaphor of a slightly flattened

watermelon. In PCA, we described the positions of seeds within the watermelon by finding

its greatest dimensions. In CVA, we are not interested in the positions of seeds in the

watermelon; instead, we want to describe the positions of the watermelons in the field

(centroids of the ellipses in Figure 7.10). If all we want to know is the location of each

melon, we could simply plot each melon’s centroids; however, suppose we want to find

the direction in which it is easiest to walk across the field without stepping on any of the

melons (perhaps we want to spread fertilizer in the field). To solve this problem, we want

to find the direction in which the melons are farthest apart. This requires that we know

chap-07 4/6/2004 17: 24 page 172

172 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

Figure 7.10 Ellipses of variation in two dimensions (X

and X

) for four sample populations. Stars

indicate locations of the means of each sample.

(PC1)

(PC2)

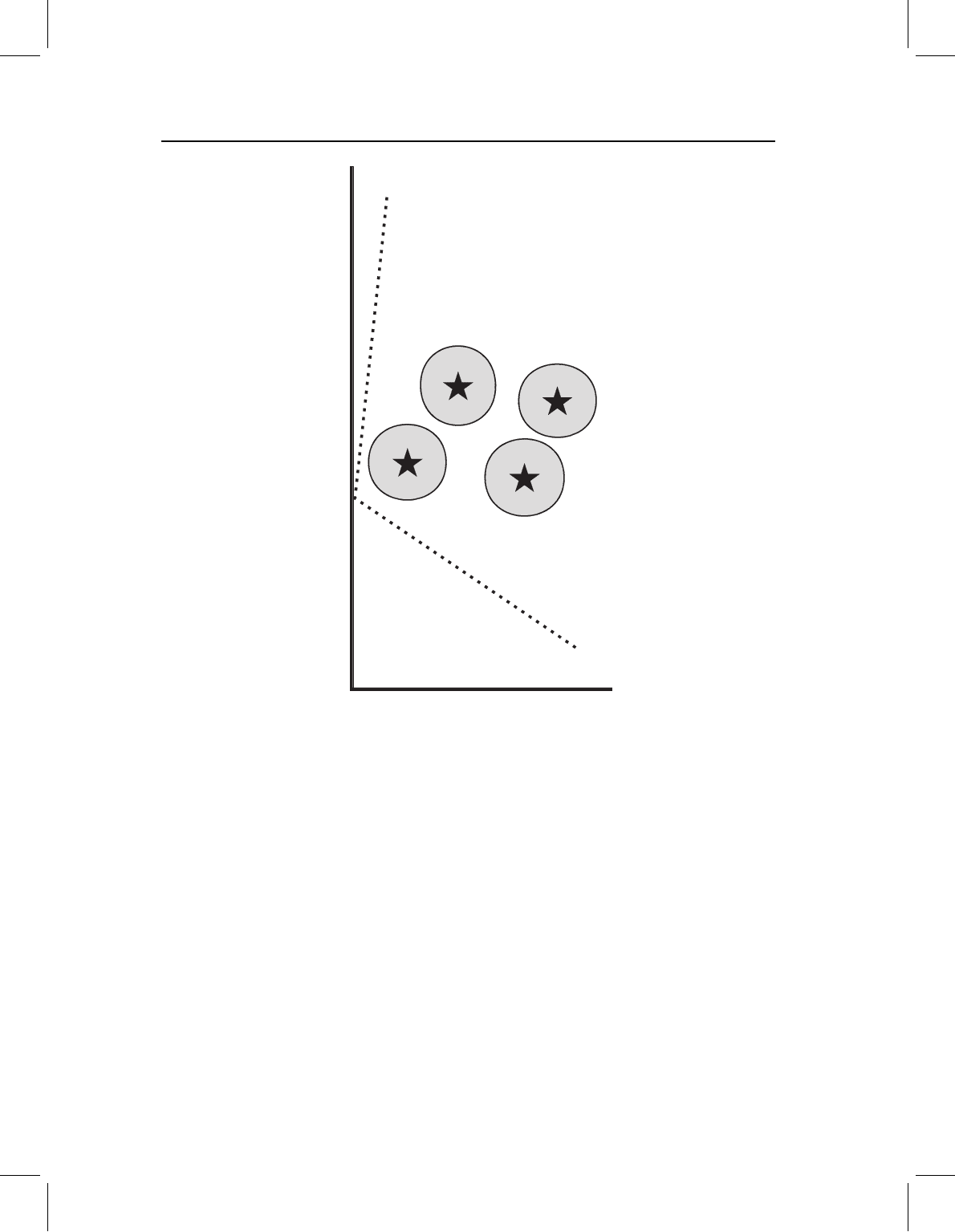
Figure 7.11 Graphical representation of the first step of CVA. The entire data set is rotated to a

new coordinate system that is aligned with the PCs of the pooled variances. At this stage the relative

positions of the four samples (and the individuals within groups) have not changed. The original

coordinate system (Figure 7.10) is shown in the dotted lines. The axes of the new coordinate system

are labeled in parentheses because we have not specified the location of the average sample, only the

directions of its variances.

the average of the shapes and orientations of all the melons, not just the position of each

melon’s centroid.

Similarly, CVA begins with a PCA of the pooled (averaged) within-group variances. This

gives us a new coordinate system in which we can describe the position of each group. In

our field, we begin by defining a new coordinate system that would be aligned with the

axes of the average melon (Figure 7.11).

chap-07 4/6/2004 17: 24 page 173

ORDINATION METHODS 173

PC1

PC2

Figure 7.12 Graphical representation of the second step of CVA. The new coordinate system (solid

lines) is rescaled in proportion to the pooled within-group variances in the original space. Variation

within samples will be circular in the new space if the original variances were all identical. Note that

the axes of the original coordinate system (dotted) are not orthogonal in the new space. Furthermore,

distances in the new space are not equivalent to distances in the original space (Figure 7.10).

Now we can see that the melons overlap more in the direction defined by the long axis

of the average melon. To take this into account, we rescale this axis proportionate to the

elongation of the average melon. In effect, we distort our plot of the field until the average

melon looks circular rather than elliptical (Figure 7.12).

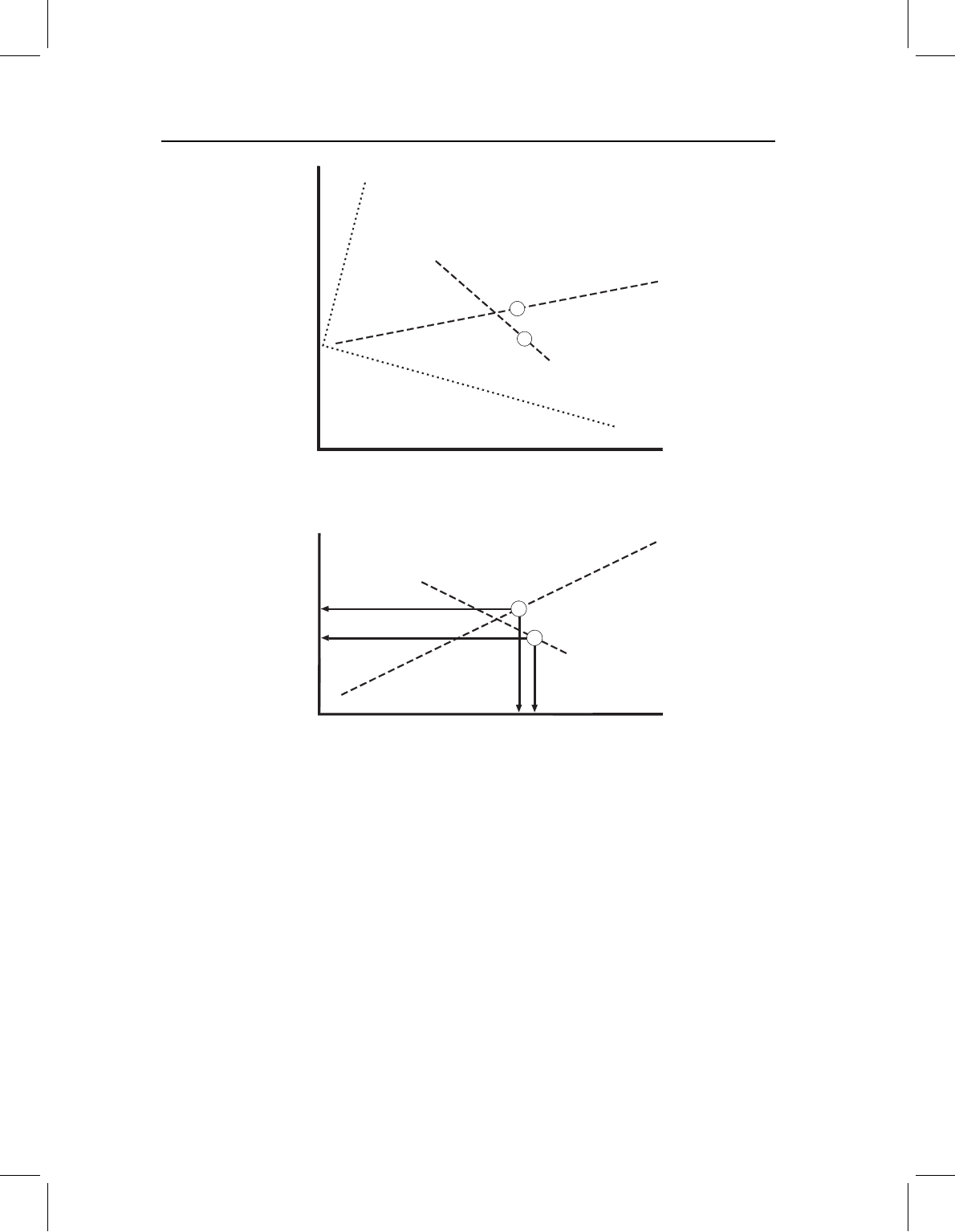
Now we can solve for the direction in which melons tend to be farthest apart in the

rescaled space by performing a PCA on the group centroids. The axes produced by this

last computation are the CVs (Figure 7.13A). The scores of individuals on the CVs are the

projections of the individuals onto these new coordinate axes (Figure 7.13B).

Because computation of the CVs involves a rescaling, interpretation of CV scores can

be complex. If we undo the rescaling and rotation that were used to solve for the CVs

(Figure 7.14), we see that each CV is a linear combination of the original variables.

chap-07 4/6/2004 17: 24 page 174

174 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

PC1

PC2

CV1

CV2

(B)PC1

PC2

CV1

CV2

(A)

Figure 7.13 Graphical representation of the final steps in CVA. (A) CV1 is the direction through

the rescaled space (outer, dashed axes) in which the group means are most different; CV2 is the

direction orthogonal to CV1 in which the group means are most different. (B) Scores of individu-

als in the CV space are their projections onto the CVs. Circles represent the scores of one of the

sample means.

However, we also see that the CVs are not orthogonal axes in the original coordinate

space. Furthermore, distances on CVs are not equivalent to distances in the original space.

Note that in this example, there are more groups than variables in the original data set.

In such cases, the number of CVs will be equal to the number of variables. Most studies

will have fewer groups than variables, and in these cases the number of CVs will be one

less than the number of groups. If there are three groups in a study, the differences among

them can be summarized as a plane defined by two vectors, whether the original data

included three variables or 300.

Algebraic description

In CVA, as in PCA, we begin with a set of measures or coordinates X =(X

, X

...X

and we want to find the vector A

=(A

, A

...A

) such that:

= A

+···+A

(7.37)

In PCA, we solved for the eigenvalues and eigenvectors of the variance–covariance matrix S.

In CVA, we are concerned with the ratio of two variance–covariance matrices: one is the

pooled within-groups variance–covariance matrix, S

, which represents the deviations of

individuals from their respective group means; the other is the between-groups variance–

covariance matrix, S

, which represents the portion of the total variance (deviations from

the grand mean) not explained by S

. In other words, S

represents differences within

chap-07 4/6/2004 17: 24 page 175

ORDINATION METHODS 175

PC1

PC2

CV1

CV2

CV1

CV2

(A)

(B)

Figure 7.14 Interpretation of CV scores in terms of the original axes. (A) Rescaling the axes has been

reversed, restoring orthogonality of X

and X

. White circles represent the scores of one individual

on each CV. (B) Rotation of the original axes is reversed, restoring the original orientation. Arrows

show projections of the CV scores onto the original axes; each CV score represents a combination

of scores on the original axes.

groups, and S

represents differences between the groups. So, in CVA we want to find

the Y

that maximizes the ratio of between-group variance to within-group variance. The

within-group variance of Y

is:

within

= A

(7.38)

and the between-group variance of Y

is:

between

= A

(7.39)

chap-07 4/6/2004 17: 24 page 176

176 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

The form of these expressions should be familiar from our discussion of PCA. As before,

we use the Lagrange multiplier λ

to form the expression:



between

within



−λ



1 −A



(7.40)

then make the substitutions indicated by Equations 7.38 and 7.39 to form:





−λ



1 −A



(7.41)

This is the expression we will maximize relative to A

, under the constraint that A

=1.

Taking the partial derivative of this expression again yields a characteristic equation that

can be solved for the eigenvalues and corresponding eigenvectors of S

−1

Interpretation of results

Results of CVA will look different from those of PCA for two crucial reasons. First,

CVA is describing differences between groups, and the direction in which group means

are most different is not necessarily the direction in which individuals are most different.

Second, CVA does not simply rotate the original data to the axes that maximize the group

differences (if it did, it would be exactly equivalent to a PCA on the group means). CVA

finds the axes that optimize between-group differences relative to within-group variation

and, in general, these axes will be different directions from the ones that maximize between-

group differences. In addition, optimization also involves rescaling such that the new

⫺0.2

⫺0.3

⫺0.4 ⫺0.3 ⫺0.2 ⫺0.1

⫺0.1

0.0

0.1

0.2

0.0 0.1 0.2

0.3

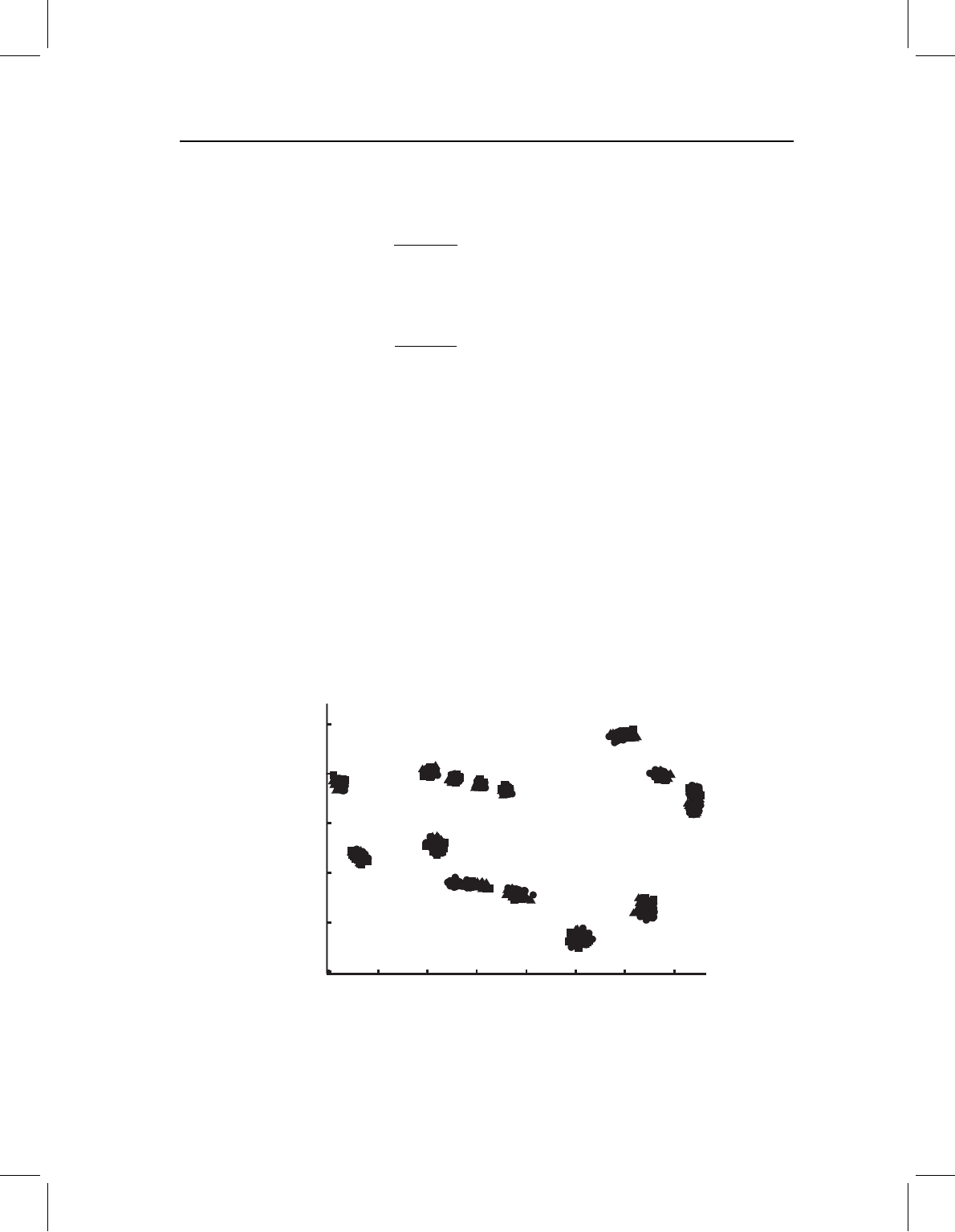
Figure 7.15 Landmark coordinates, in partial Procrustes superimposition, for 119 squirrels from

three geographic samples. Circles =western Michigan, squares =eastern Michigan, triangles =

southern states.

chap-07 4/6/2004 17: 24 page 177

ORDINATION METHODS 177

axes are scaled differently from the original axes and scaled differently from each other.

Consequently, distances in CV space can be quite different from distances in the original

data, and interpretations of results can be counterintuitive.

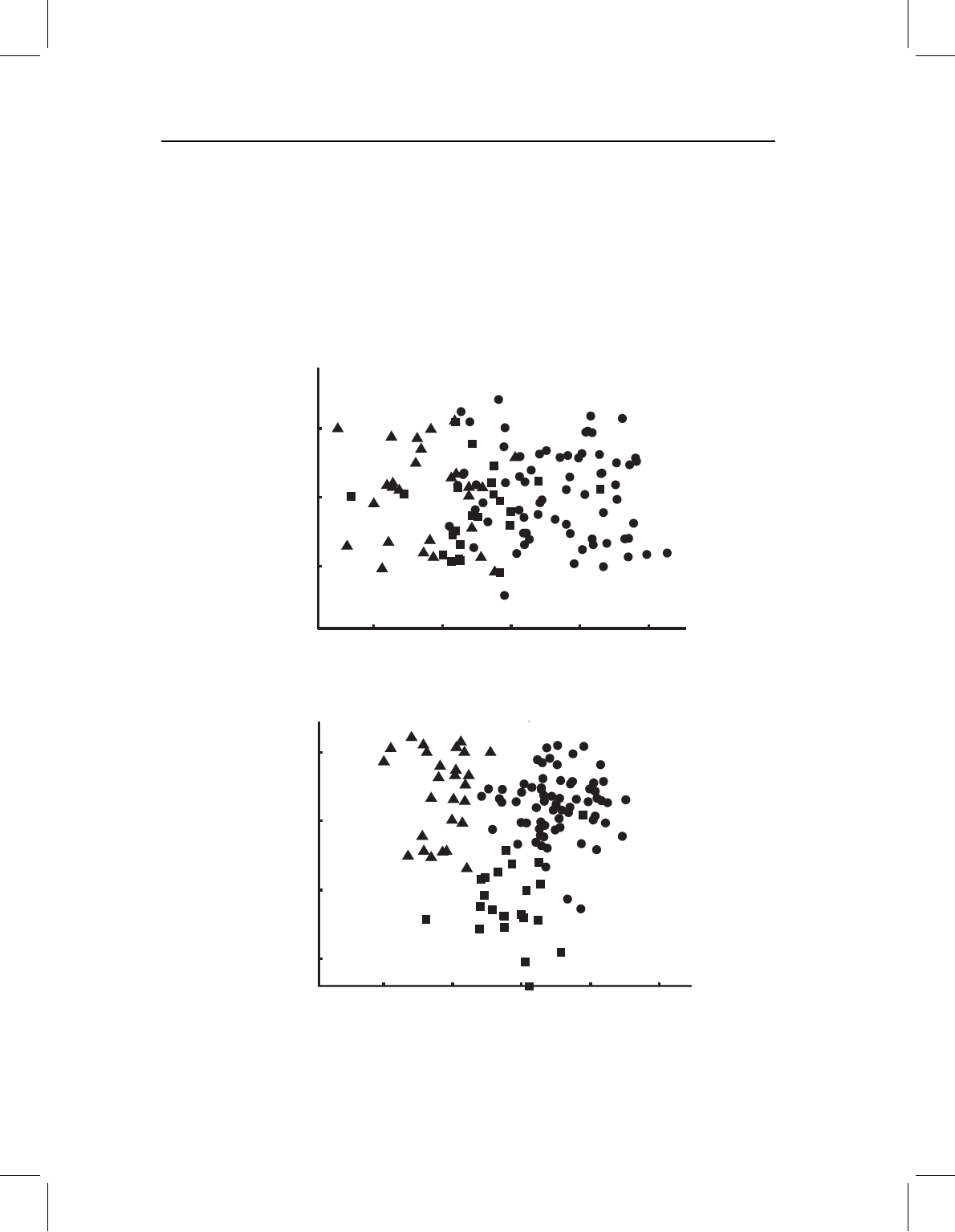
To illustrate the differences between PCA and CVA, we show results from performing

each on the same data set. This data set is composed of 15 landmarks on the lower jaws

of 119 squirrels from three geographic areas. As shown in Figure 7.15, the distribution

of shapes in the three groups overlaps broadly, and this broad overlap is reflected in

the plot of the first two PCs (Figure 7.16A). Clearly, the combination of shape variables

⫺0.02

⫺0.04 ⫺0.02

0.00

0.02

0.00 0.02

0.04

PC1

PC2

⫺0.004

⫺0.008

⫺0.008 ⫺0.004

0.000

0.004

0.000 0.004 0.008

CV1

CV2

(A)

(B)

Figure 7.16 Scatter plots from PCA (A) and CVA (B) of 119 squirrel jaws from three geographic

areas. Circles =western Michigan, squares =eastern Michigan, triangles =southern states.