Yangsheng Xu, Yongsheng Ou. Control of Single Wheel Robots

Подождите немного. Документ загружается.

el-based

Con

trol

measured fromAtoO(the origin of theframe), Gyrover’s orientation θ with

respect to the inertial frame, anddeﬁning ψ = θ − α as theangle measured

between the vehicle principalaxis andthe distance vector e .When e =0,

eﬁ

tion

θ and ψ .T

hen

ollow

ing

equations

btained

˙e = Ru

ψ = − u

− S

(3.48)

where C

:= cos ( ψ ), S

:= sin ( ψ )and e =0.Moreover, we deﬁne ψ =0and

ψ = − u

,if e =0.

On the basis of the previous considerations, we arenow ready to ad-

dressthe aforementioned closedloopsteeringprobleminthe following general

terms.

Let the robot system be initially located at anynon-zerodistance from

the inertial frame and assume that all state variablesrequired aredirectly

measurable. Then ﬁndasuitable, if any, state feedbackcontrol law[u

]

whichg

uarant

ees the state

[

e, β − π/2 ,

β ]t

symptotically driven to the

null point[0 , 0 , 0]

,whileavoidingany attainmentofthe conditions of β =0

(or β = π )i

ﬁnitetime.

Proposed Controller

Proposition 2 Consider the system (3.47) with the feedbackcontrol laws u

and u



= − k

Sgn ( C

) Sgn ( β − π/2+

β )

= − ( k

e + u

) Sgn ( C

)

(3.49)

where Sgn , K

and k

aredeﬁned in Equations (3.50) and (3.51), k

is a

sitivescalarconstantand

− 1,w

hichc

an be

designed.

Anystate ( e, β − π/2 ,

β )starting fromthe domain D deﬁnedby

D = { ( e (0),β(0) − π/2 ,

β (0))| e>0 , 0 <β<π,



( β − π/2)

+(β − π/2+

β )

/ 2 <π/ 2 ,

e, β,

β ∈ R

}

converges to

thep

oint

, 0 , 0]

Proof: First, let Sgn (.) be asign function described as follows:

Sgn ( x )=



1 ,ifx≥ 0

− 1 ,ifx< 0

(3.50)

Let k

> 2beapositivescalarconstant,which can be designedand should

be less then ˙α

mam

.Let



+ I



2(β − π/2+

β )



+ f

) / ( J

) .

(3.51)

3.2

Non

linear

del

Set

V = V

+ V

=(( β − π/2)

+(β − π/2+

β )

) / 2

= e

/ 2 .

(3.52)

Thetime derivative

V is given by

V =

where

=2( β − π/2)

β +(β − π/2+

β )(

β +

β )

Substituting Equations(3.51) and(3.49) into Equation (3.47), we obtain

( β − π/2+

β )

β = − ( G

+ IC

)(β − π/2+

β )

−



( G

+ I

)(β − π/2+

β )



− J



β − π/2+



− 2(β − π/2+

β )

≤−2(β − π/2+

β )

suchthat

≤−( β − π/2)

−

− ( β − π/2+

β )

Thus V

is po

sitivedeﬁnite and

is negatived

eﬁnite. The

remainingp

rob-

lem concerns why β will not reach0or π during theentire process. Since

| β − π/2 |≤



(0) <π/ 2and V

is monotonically non increasing,they

guarantee0<β<π.

= e ˙e

= − eR | C

| ( k

e + u

)

≤−k

R | C

Since R , k

, k

, S

and u

arep

ositive,

≤ 0. In fact,

is strictly negative,

except when

e =0

(3.53)

In these cases

=0.Equation (3.53)presents two possible solutions for the

system.

Moreover, C

=0is not asolution,whichisevidentfromEquation(3.48).

By substituting u

and u

into Equation(3.48),wehave

ψ = Sgn ( C

)(k

Sgn ( β − π/2+

β )+S

( k

e + u

) /e) .

Because β → π/2,

β → 0and C

→ 0, u

will vanish. Thus we obtain

ψ = Sgn ( C

)(k

Sgn ( β − π/2+

β )+k

) .

Since k

− 1 >k

> 0, during anysampling period,

ψ is not zero. Hence, any

system trajectory startingfromaset in C

=0will not remain there. Thus,

e =0is the only solution, according to the LaSalle Propositionfor nonsmooth

systems in [95]. Therefore, the proposition is proven.

el-based

Con

trol

3.2.3Line TrackingControl

Foramobile robot,suchasGyrover, most traveling tasks can be realizedby

following connected segments of straightlines. Forexample, Figure 3.14shows

amobilerobot’stravelpath alongaseries of connectedcorridors.

ealize

the

straigh

ine

llo

wing

while

eping

rti-

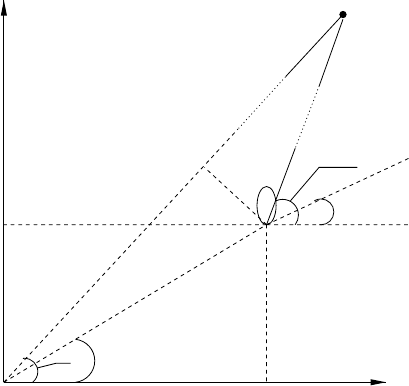
cal is ourcontrol problem. As depicted in Figure3.15,where ( x

)isthe

coordinate of the second point, let us consider Gyroverinitiallypositioned

at aneighborhood of theorigin (i.e., thestart point) and standing almost

vertically, abouttotakeastraightline so as to approachthe second point.

Robot

door

Lab

Fig. 3.14. The robot’s path along connected corridors.

Let us

deﬁne

r , e and d ,w

hichare nonnegative,asthe distancesfromA

to the origin, the line andthe second point, respectively. θ and φ aredeﬁned

as in Figure 3.15. Then,wehavethe following equations











e ˙e = rRu

φ − α

φ − θ

d = pRu

p = rC

θ − α

−



+ y

φ − α

= − dC

ϕ − α

where S

φ − α

:= sin ( φ − α ), S

φ − θ

:= sin ( φ − θ ), C

φ − θ

:= cos ( φ − θ ), and

ϕ − α

:= cos ( ϕ − α ).

On thebasisofprevious considerations, we arenow readytoaddressthe

aforementioned closedloopline trackingproblemingeneral terms.

Let the robot initially locate at some neighborhood of theorigin andas-

sume that all state variablesbedirectly measurable; then ﬁndasuitable (if

3.2

Non

linear

del

( x y)

Fig. 3.15. The parameters in the line tracking problem.

any) feedback control law[u

]

that guarantees the state [ β − π/2 ,

β,e, d ]

to be

asymptoticallydriven to the point[0

, 0 , 0 , 0]

hilea

voidingany

at-

tainmentofthe conditionsof β =0(or β = π )inﬁnitetime.

Proposition3Consider the system (3.47) with the feedbackcontrol la

and u



= − k

Sgn ( S

φ − α

φ − θ

) Sgn ( β − π/2+

β )

= − ( f

+ u

) Sgn ( S

φ − α

φ − θ

)

(3.54)

where f

is deﬁned in Equation(3.56).

Anys

tate, startingf

rom[

β (0) − π/2 ,

β (0),e(0),d(0)] with 0

<β(0) <π

and e (0) > 0, converges to thepoint [0, 0 , 0 , 0]

Proof:

First, we

introduce some

deﬁnitions.

Sgn ( . ), f

and u

aredeﬁned as in Equations(3.50) and(3.51).

Let Θ (.) be

ign function described

follows:

Θ ( x )=



1 ,ifx≥ 0

0 ,ifx< 0 .

(3.55)

We let

= k

Θ ( pSgn( S

φ − α

φ − θ

)) (3.56)

where k

is apositive scalarconstantwhichcan be designed andshould be

less than ˙γ

max

el-based

Con

trol

V = V

+ V

=(( β − π/2)

+(β − π/2+

β )

) / 2

= e

/ 2

= d

/ 2

(3.57)

Thetime derivative

V is given by

V =

where

=(β − π/2)

β +(β − π/2+

β )(

β +

β )

≤−( β − π/2)

− ( β − π/2+

β )

= e ˙e

= − rR | S

φ − α

φ − θ

| ( f

+ u

)

= d

= pRu

Since r , R , f

and u

aren

onnegative,

≤ 0. This meanst

hatt

he ﬁrst

term e is alwaysnon increasingi

ime andinthe consequence. If

d =0is

maintained, e is also zero. Moreover, fromFigure 3.15, S

φ − θ

=0an

e =0

can be deduced from eachother.˙α will never be zero, for ˙α = u

ecause

is aconstantvalue, it is trivial to know that e will not stop decreasing until

e =0.

is po

sitivedeﬁnite and

is negatived

eﬁnite. At

theb

eginning

β is

nearvertical, so that during theentire process, β ≈ π/2issustained.That

means cos

β → 0and u

=0.Byomitting them,

= − k

pSgn( S

φ − α

φ − θ

) Θ ( pSgn( S

φ − α

φ − θ

)).

thus,

is negatives

emi-deﬁnite. As

with

the

previous process, it is trivial

to prov

hatt

he only solution of thesystem, for

=0is d =0.T

prove theproposition.

3.2.4 Simulation Study

The following simulation study is basedonrobot system parameters as shown

in Table 3.2.

m [ kg] R [ m ] g [ m/s

] I

[ kgm

] I

8.05 0.17 9.8 0.116 0.116 0.232

Table 3.2. Physicalparameters.

Set

3.2

Non

linear

del

Balance Control

With regard to balance control, the initial condition seems to be toonarrow

fort

constrain

σ<

π/

mak

sma

diﬁcationt

thecontroller can be usedinawider rangeofinitialconditions.

= − ((2 + k

)(β − π/2) +(3+2k

)

β +(2+k

)

β + h

( t )

β + h

( t ) u

) /h

( t )

where k

is apositive number,whichcan be designed.Toprove the subsys-

tem β,

β,

β is

asymptotically

stabilized,

cons

ider

ollow

ing

apunov

functioncandidate

∗

=(β − π/2)

/ 2+(

β + β − π/2)

/ 2+(

β +(1+k

)(

β + β − π/2))

/ 2 .

Its derivativeis

∗

= − ( β − π/2)

− k

(

β + β − π/2)

− (

β +(1+k

)(

β + β − π/2))

We completed two sets of simulationsfor balance control to compare the

diﬀerent

eﬀects of

he initial parameters areshown

Table 3.3.

[ rad ]

[ rad/s] ˙α

˙γ

π/4 3 8 -8.660381

Table 3.3.

Initialparameters in

balance control.

In theﬁrst simulation, k

=10, thetarget andother gain parameters are

shown in Table 3.4.

[ rad ]

[ rad/s] ˙α

˙γ

π/2 0 0 0 10 1

Table 3.4. Target and gain parameters in balance control I.

Thetime span of thesimulationisfrom0to16.0s.The results areshown

in Figures 3.16, 3.17, 3.18 and3.19 .

In the second simulation,except for

=1,all other parameters arethe

same as in theﬁrst simulation.

The time span of thesimulationisfrom0to16.0s.The results areshown

in Figures 3.20, 3.21, 3.22 and3.23 .

Even thoughitispossible that the states in simulation II will converge,

the control process in simulation Iisfaster andsmoother.

el-based

Con

trol

0 2 4 6 8 10 12 14 16

0.7

0.8

0.9

1.1

1.2

1.3

1.4

1.5

1.6

Time (s)

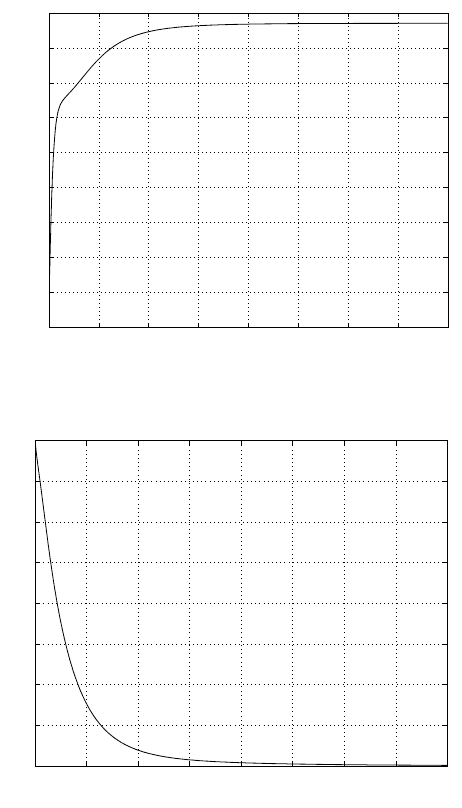
Fig. 3.16. Leaning angle β in balance control.

0 2 4 6 8 10 12 14 16

Time (s)

˙α

Fig. 3.17. Precession angle velocity ˙α in balance control.

PositionControl

We have set the initial values of thesimulation in Table 3.5.

The target parameters areshown in Table 3.6.

The time span of thesimulation is from0to16s. Theresults areshown

in Figures 3.24, 3.25, 3.26 and3.27.

This simulation demonstratesthatthe proposed pointtopoint controller

is correct.

3.2

Non

linear

del

0 2 4 6 8 10 12 14 16

−9

−8

−7

−6

−5

−4

−3

−2

−1

Time (s)

˙γ

Fig. 3.18. Driving speed ˙γ in balance control.

0 2 4 6 8 10 12 14 16

−10

−8

−6

−4

−2

Time (s)

˙γ

˙α

Fig. 3.19. Parameters of ˙α, β,

β, ˙γ in balance control.

Line TrackingControl

Theaim of the simulation is to trackastraight line so as to demonstrate the

eﬃciency of the proposed line trackingcontroller.Fromthe neighborhood of

an origin, therobot is drivenalong astraight line to reachthe point(3,4).

The initial values of the simulation areshown in Table 3.7.

Thetarget parameters areshown in Table 3.8.

el-based

Con

trol

0 2 4 6 8 10 12 14 16

0.7

0.8

0.9

1.1

1.2

1.3

1.4

1.5

1.6

Time (s)

the

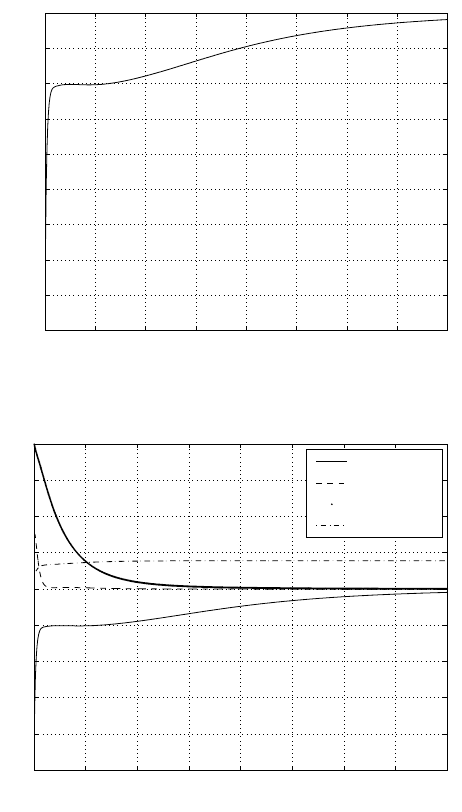
Fig. 3.20. Leaning angle β in balance control II

0 2 4 6 8 10 12 14 16

Time (s)

˙α

Fig. 3.21. Precession angle velocity ˙α in balance control II.

The time span of thesimulation is from0to32s. Theresults areshown

in Figures 3.28, 3.29, 3.30 and3.31.

Here, large values of k

and k

arebetter, however, theyshould be less

than the ˙α

max

and˙γ

max

,respectively.

Despite this, thereare some drawbacks in thecontrol process. The ﬁrstis

the system states exhibit highly oscillatorybehavior and the second is that

controlinputs sometimesneed to switchtoo sharply andfast.Both will cause

diﬃculties forreal time controland result in worse performance.Tosolve

3.2

Non

linear

del

0 2 4 6 8 10 12 14 16

−9

−8

−7

−6

−5

−4

−3

−2

−1

Time (s)

˙γ

Fig. 3.22. Driving speed ˙γ in balance control II.

0 2 4 6 8 10 12 14 16

−10

−8

−6

−4

−2

Time (s)

˙γ

˙α

Fig. 3.23. Parameters of ˙α, β,

β, ˙γ in balance control II.

these problems, we propose to replace thesign functions in the controllers

with tanh functions.

Deﬁnition 3 Tanh( . )isabipolar function described as follows:

Tanh( x )=

1 − e

− k

1+e

− k

(3.58)

where k

is apositive scalarconstant, whichcan be designed. Tanh( . )isshown

as in Figure 3.32.