Yangsheng Xu, Yongsheng Ou. Control of Single Wheel Robots
Подождите немного. Документ загружается.


4
Learning-based Control
4.1 LearningbyCNN
Due to
the
complexity
of thesystem, it
is
difficult for us
to
work outa
“com-
plete”analyticalmodel of it. Therefore, in this chapter, we propose using
amachine learning algorithm, CascadeNeural Network (CNN) with node-
decoupledextended KalmanF
iltering(
NDEKF), to
mo
delthe robot’s be
hav-
iors fromhuman control strategy (HAS).
Motivation
Gyroverisasingle trackmobilevehiclewhichisinherently unstable in the
lateral direction. With the lack of awide polygonofsupport(single-point
contact with
the
ground), Gyroverhas very badstatic stability,
even though
it is equipped with an internal gyroscope spinningatahigh rate. The thin
pneumatic tire whichi
sw
rapped around the robotmakes
it
difficult to stand in
astationary position foravery long time, it will fall on theground. However,
by tilting the internal gyroscope into differentorientations, we can indirectly
control the lean angle of therobot, whichimplies that it is possible forusto
keep the robottostayinits uprightposition with apropercontrol method.
Previous researchofGyroverhas been focused on dynamics andcontrol,
including the kinematicconstraints andmotion equations[74, 107, 115, 6, 5,
113, 114]. However, the robotconcept bringsanumber of challengingprob-
lems in modeling andcontrol because of thehighly coupled dynamics,the
nonholonomicconstraints andthe non-minimumphase behavior of thesys-
tem. The proposed linear state feedbackmodel in [6]only guarantees thelocal
stabilityofthe system.Moreover, the dynamicmodel derivedhas been based
on manyassumptions whichmay notberealistic.
In [5], alinear state feedbackcontroller is developed for stabilizingthe
robottoany desiredangle,however, this modelonly applied forthe case when
therobot reaches steady state. By consideration of the swinging motion of the
Y. Xu and Y. Ou: Control of Single Wheel Robots, STAR 20, pp. 73–117, 2005.
© Springer-Verlag Berlin Heidelberg 2005
74 4 Learning-based Control
internal mechanism, the model is modified in [113]. Unfortunately, the models
obtained above are based on the assumption of rolling without slipping, that
is, the robot must be rolling perfectly on the ground. Therefore, these models
are not applicable for the static situation. In the static situation, the coupling
between the wheel and the flywheel becomes much more complicated, which
makes it difficult to derive an analytical model by traditional control methods.
On the other hand, humans are capable of mastering complex and highly
nonlinear control systems. A typical example is car driving. For Gyrover con-
trol, humans are able to control the robot well if enough practice is undertaken.
Thus, we intuitively come up with the idea of machine learning, a model-free
approach to model this kind of human control strategy. This approach is suit-
able for Gyrover control for the following reasons:
• Gyrover is a complex system, for which it is difficult for us to develop
a complete dynamic model to represent the robot’s behaviors by using
traditional control methods.
• From a practical point of view, it is equally difficult to model the system
precisely due to some unmodeled factors, such as friction. Friction is an
important issue when we are dealing with the coupling between the wheel
and the spinning flywheel.
• Although Gyrover is a complex system, humans can control the robot
through a radio transmitter to perform various kinds of task. They do
not need to explicitly model a system in order to control it. Through
interaction with the system and observation of the behaviors of the system,
humans are able to “learn” how to control a system.
• The learning process is in fact a direct input-output mapping between the
system sensory data and the actuation data. A controller is generated by
using the training data while a human “teacher” controls the system until
the synthesized controller can perform the same way as a human.
4.1.1 Cascade Neural Network with Kalman Filtering
The field of intelligent control has emerged from the field of classical control
theory to deal with applications which are too complex for classical control
approaches. In terms of complexity, human control strategy lies between low-
level feedback control and high-level reasoning, and encompasses a wide range
of useful physical tasks with a reasonably well-defined numeric input/output
representation.
Here, we introduce a continuous learning architecture for modeling hu-
man control strategies based on a neural network. Since most neural networks
used today rely on rigid, fixed architecture networks and/or with slow gra-
dient descent-based training algorithms, they may not be a suitable method
to model the complex, dynamic and nonlinear human control strategy. To
counter these problems, a new neural network learning architecture is pro-
posed in [78], which combines (1) flexible cascade neural networks, which
4.1
Le
arningb
yC
NN
75
dynamicallyadjust the size of theneural network as part of thelearningpro-
cess, and (2)node-decoupled extended KalmanFiltering(NDEKF), afaster
converging alternative to exappropriation.This methodology hasbeen proved
whic
hc
an
efficien
tlym
od
el
hu
man
co
nt
rols
kills
[76],
[11
6]
an
dh
um
an
sensa-
tion[
62].
First of all, let’s discuss the architectureofcascadelearning. In cascade
learning, the network topology is notfixed prior to learning,hidden units are
added to an initially minimal network oneatatime. This notonly frees us
fromapriorchoice of network architecture, butalso allows new hiddenunits
to assume variable activation functions. Thatis, each hidden unit’s activation
functionnolonger needs to be confined to justasigmoidal nonlinearity. A
priori assumptionabout theunderlying functionalformofthe mapping we
wish
to
learn
is
th
us
min
imized.T
he
whole
tr
ainingp
ro
cess
is
de
scrib
ed
be
lo
w:
1. Initially,nohidden unit exists in the network, only direct input-output
connections. These weights aretrainedfirst,toobtain alinear relationship,
if any.
2. With no furthers
ignificantd
ecrease in the RMS
error (
e
RMS
), afi
rst
hiddennodewill be introduced into the network fromapool of candidate
units. Thesecandidate unitsare trainedindependently
and in
parallel
with differentrandomi
nitialw
eigh
ts
by
using the quickprop algorithm.
3. The best candidate unit will be selected and installed into the network
if no more appreciable errorr
eduction occurs, therefore, the
first hidden
node is produced.
4. Once theh
idden unit is
installed,
all the
input we
ights
of
thehidden
unit will be frozen, whilethe weights to the outputunit(s)is/are going
to train again.This allowsfor amuchfaster convergenceofthe weights
during trainingt
hana
standard mu
lti-laye
rf
eedforward netwo
rk.
5. This process (fromstep 2-step 4) is repeated until the e
RMS
reduces
sufficiently forthe training setorthe number of hidden units reaches a
predefined maximumn
um
ber.
Figure 4.1 illustrates, for example, howatwo-input, single-outputnetwork
with abias unit growswith increasing number of hidden nodes.
Acascadeneural network with n
in
input units(includingthe biasunit), n
h
hiddenunits, and n
out
,has n
w
connections (totalnumberofweights) where,
n
w
= n
in
n
out
+ n
h
( n
in
+ n
out
)+(n
h
− 1)n
h
/ 2(4.1)
In fact, anymulti-layerfeedforward neuralnetwork with
k hiddenunits
arranged in m layers, fullyconnectedbetween consecutivelayers, is aspecial
case of acascadenetwork with
k hiddenunitswith some of the weights equal
to zero. Thus, this architecturerelaxes apriorassumptions aboutthe func-
tional form of themodel to be learntbydynamically adjusting the network
size.Wecan furtherrelax these assumptions by allowing new hiddenunits
to have different activation functions. The kind of activationfunctions which
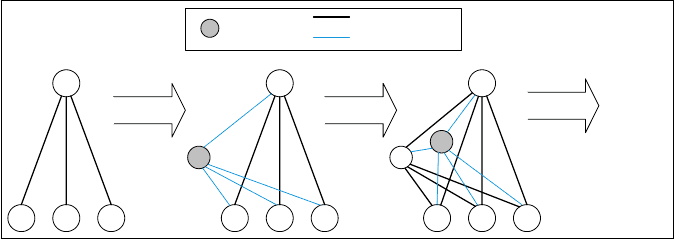
76 4 Learning-based Control
Bias IN
2
IN
1
OUT
Bias IN
2
IN
1
OUT
H
1
H
2
Bias IN
2
IN
1
OUT
H
1
established connection
new connection
new node
add 1st hidden
node
add 2nd hidden
node
and so on
. . . . . .
Fig. 4.1. The cascadelearning architecture.
reduces e
RMS
most
will
be
selected
duringt
he
pro
cess,S
igmoid,
Gaussian,
and sinusoidal functions of various frequencyare some of theavailable types
of activation functions we can choose.
While quickpropisanimprovementoverthe standard exappropriation al-
gorithm fora
djusting the weights in the cascade network, it stillrequires many
iterations until satisfactory convergence is reached. When combining cascade
neuralnetworks with node-decoupledextended Kalmanfiltering(NDEKF),
[76] hass
hown thatthis methodology can solvethe po
or
lo
calminima prob-
lem, and that theresultinglearningarchitecture substantially outperforms
other neuraln
etwo
rk training paradigms in
learnings
peed and/or error con-
vergencefor learning tasks importantincontrol problems.
4.1.2 Learning architecture
Denote ω
i
k
as theinput-side weightvector of length n
i
w
at iteration k ,for
i ∈{0 , 1 ,...,n
o
} ,and,
n
i
w
=
n
in
+ n
h
− 1 i =0
n
in
+ n
h
i ∈{1 ,...,n
o
}
(4.2)
The NDEKF weight-update recursion is givenby, (starting fromequa-
tion(3.6) to (3.9), {}’s, ()’s and[]’s evaluate to scalars, vectors andmatrices
respectively)
ω
i
k +1
= ω
i
k
+ { ( ψ
i
k
)
T
( A
k
ξ
k
) } φ
i
k
(4.3)
where ξ
k
is the n
o
-dimensional error vector for the currenttraining pattern,
ψ
i
k
is the n
o
-dimensional vector of partial derivatives of the network’soutput
unit signals with respect to the
i th unit’s netinput, and,
4.1
Le
arningb
yC
NN
77
φ
i
k
= P
i
k
ζ
i
k
(4.4)
A
k
=
I +
n
o
i =0
{ ( ζ
i
k
)
T
φ
i
k
} [ ψ
i
k
( ψ
i
k
)
T
]
− 1
(4.5)
P
i
k +1
= P
i
k
−{( ψ
i
k
)
T
( A
k
ψ
i
k
) } [ φ
i
k
( φ
i
k
)
T
]+η
Q
I (4.6)
P
i
0
=(1 /η
P
) I (4.7)
where ζ
i
k
is the n
i
w
-dimensional input vector for the i th unit, and P
i
k
is the
n
i
w
× n
i
w
approximate conditional errorcovariance matrix forthe i th unit.
The
pa
rameter
η
Q
is introduced in (3.9)toavoid the singularityproblems for
error covariance matrices.Throughout thetraining,weuse η
Q
=0. 0001 and
η
P
=0. 01.
Thevector ψ
i
k
can be computed in this way:let O
i
be the value of the
i th outputnode, Γ
O
be its corresponding activation function, net
Oi
be its net
activation, Γ
H
be the activationfunctionfor thecurrenthidden unitbeing
trained,and net
H
be
its netactivation. We
ha
ve,
∂O
i
∂net
Oj
=0, ∀ i = j (4.8)
∂O
i
∂net
Oi
= Γ
O
( net
Oi
) ,i∈{1 ,...,n
o
} (4.9)
∂O
i
∂net
H
= w
Hi
· Γ
O
( net
Oi
) · Γ
H
( net
H
)(
4.10)
where w
Hi
is the weightc
onnecting thecurrenthidden no
de
to
the
i th output
node.
4.1.3 Modelevaluation
The main advantage of modeling arobot’sbehaviors by learning, is that no
explicit physical mo
delisrequired, ho
wever, this also presents
its
biggest
weakness. Sinceamodel is trained by theinput-output relationship only,the
lackofa
scien
tific justificationdegrades the confidence that
we
can
show
in
these learntmodels. This is especially truewhen the process we aregoing
to model is
dynamic and sto
ch
astic in
nature, whichi
st
he case in hu
man
control strategy. Foradynamicprocess,errors mayfeed backintothe model
to produce outputs whichare notcharacteristics of theoriginalprocess or
makethe process unstable.For astochastic process,astatic error criterion
such as RMSerror, basedonthe difference between the trainingdata andthe
predicted modeloutputsisinadequate to gaugethe fidelityofalearntmodel
to thesource process.
In general, for differentmodels, the similaritybetween adynamic human
control trajectory andamodel-generated one will vary continually,fromcom-
pletely dissimilartonearly identical. Furthermore, onecannotexpect exact
trajectories forthe system andthe learnt model, even if equivalentinitial

78 4 Learning-based Control
conditions are given. To effectively evaluate the learnt models, we introduce
a stochastic similarity measure proposed in [77]. This method is based on
Hidden Markov Model (HMM) analysis, which is a useful tool for comparing
stochastic, dynamic and multi-dimensional trajectories.
Hidden Markov Model is a trainable statistical model, which consists of a
set of n states, interconnected by probabilistic transitions, each of these states
has some output probability distributions associated with it. A discrete HMM
is completely defined by,
λ = { A, B, π } (4.11)
where A is the probabilistic n
s
× n
s
state transition matrix, B is the L × n
s
output probability matrix with L discrete output symbols l ∈{1 , 2 , . . . , L } ,
and π is the n -length initial state probability distribution vector for HMM.
Two HMMs (λ
1
and λ
2
) are said to be equivalent if and only if,
P ( O | λ
1
) = P ( O | λ
2
) , ∀ O (4.12)
We prefer discrete HMMs rather than continuous or semi-continuous
HMMs, because they are relatively simple in computation and less sensitive
to initial random parameter settings. However, the human control trajectories
we are going to measure are continuous and real-valued functions. In order to
make use of the discrete HMMs, we must convert the data sets into sequences
of discrete symbols O
n
by the following procedures:
1. Normalization
2. Spectral conversion
3. Power Spectral Density (PSD) estimation
4. Vector quantization
The purpose of steps (1) - (3) is to extract some meaningful feature vectors
V for the vector quantizer. In step (4), the feature vectors V are converted to
L discrete symbols, where L is the number of output observable in our HMMs.
In general, assume that we are going to compare the observation sequences
(
¯
O
1
and
¯
O
2
)fromtwo stochastic processes ( Γ
1
and Γ
2
). The probabilityof
the observation sequences
¯
O
i
given theHMM model λ
j
,isgiven by [77],
P
ij
= P (
¯
O
i
| λ
j
)
1 /
¯
T
i
,i,j ∈{1 , 2 } (4.13)
wherethe aboveequation is normalizedwith respect to the total numbers of
symbols
¯
T
i
.
The similaritymeasure σ between
¯
O
1
and
¯
O
2
is,
σ (
¯
O
1
,
¯
O
2
)=
P
12
P
21
P
11
P
22
(4.14)
Figure 4.2 illustratesthe overall approachtoevaluate the similaritybe-
tween two observation sequences. The HMMsare trained by eachobservation
sequence first,then we cross-evaluate eachobservation sequence on theother
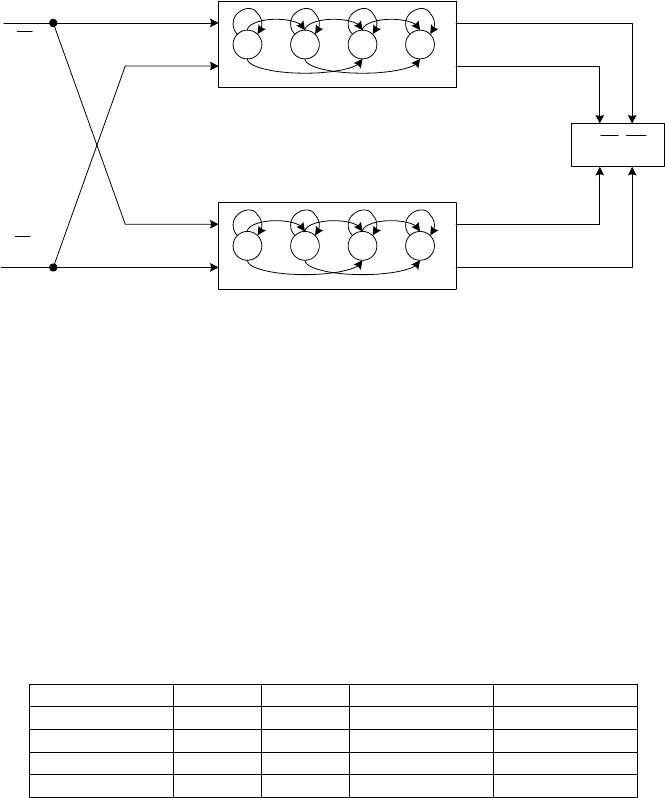
4.1
Le
arningb
yC
NN
79
S
1
S
4
S
3
S
2
),(
21
OO
S
1
S
4
S
3
S
2
O
1
O
2
P
11
P
21
P
12
P
22
1
2
HMM1:
HMM2:
σ
λ
λ
Fig. 4.2. Similaritymeasure between
¯
O
1
and
¯
O
2
.
HMM.Basedonthe four normalizedprobabilities, the similaritymeasure
σ
can be obtained.
Here, we
demonstrate an example of
ho
wthis similarity
measure works.
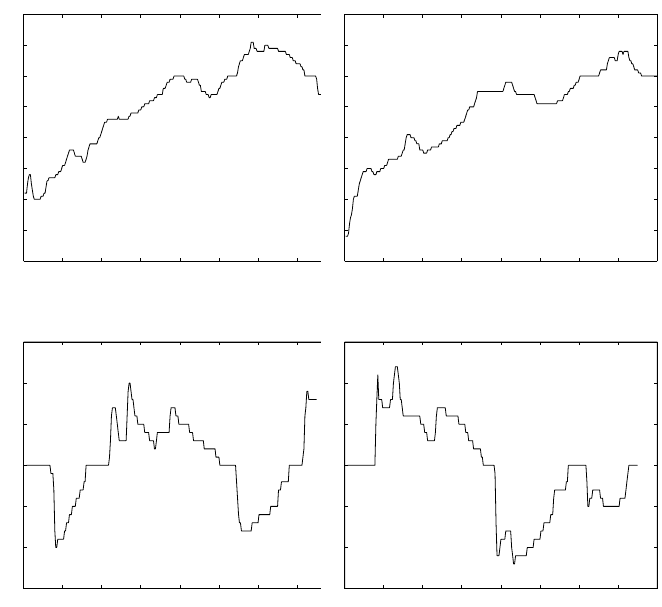
Figure 4.3 shows four Gyrover control trajectories. Figure 4.3(a) and 4.3(b)
correspond to the tiltup motioncontrol, whileFigure 4.3(c) and 4.3(d) cor-
respond to
the
lateral stabilizationc
ontrol of Gyrove
r. We
applied theHMM
similaritymeasure across these four trajectories. We mightexpect that the
trajectories of
thesame motion should have
ar
elatively high similarityand
thatany two trajectories whichweregenerated fromdifferentkindsofmotion
should have alow similarityvalue. We summarize the results in Table 4.1.
Tiltup#1 Tiltup #2 Ve
rtical stab. #1
Ve
rtical stab. #2
Tiltup#1 1.000 0.6306 0.0524 0.1234
Tiltup#2 0.6306 1.000 0.0615 0.0380
Vertical stab. #1 0.0524 0.0615 1.000 0.4994
Ve
rtical stab. #2
0.1234 0.0380 0.4994 1.000
Table 4.1.
Similaritymeasures be
twe
en differentcontrol trajectories.
From Table 4.1, it is clearthatthis similaritymeasure canaccurately
classify dynamic controltrajectoriesfromthe same type of motion,while
discriminating those fromdifferentmotionsbygiving alow similarityvalue.
Thissimilaritymeasure canbeapplied towards validating alearned model’s
fidelitytoits trainingdata, by comparing the model’s dynamic trajectories in
the feedbacklooptothe human’s dynamic controltrajectories.
80 4 Learning-based Control
0 1 2 3 4 5 6 7 8
120
130
140
150
160
170
180
190
200
time
Tilt command
Tiltup control trajectory #1
(a)Tiltup1
0 1 2 3 4 5 6 7 8
120
130
140
150
160
170
180
190
200
time
Tilt command
Tiltup control trajectory #2
(b)Tiltup2
0 1 2 3 4 5 6 7 8
165
170
175
180
185
190
195
time
Tilt command
Vertical stabilization control trajectory #1
(c)V
erticalbalancing 1
0 1 2 3 4 5 6 7 8
165
170
175
180
185
190
195
time
Tilt command
Vertical stabilization control trajectory #2
(d)Verticalbalancing 2
Fig. 4.3. Control data for differentmotions.
4.1.4Training procedures
Fist of all, we have made two assumptions forthe training data provided for
the learning pro
cess:
1. Reliable training set.
Sincel
earningi
sak
ind of high-level, mo
delfree
“teaching by showing” approach, the stabilityorrobustnessofthe learnt
model heavily dependsonthe operating skills of a“human teacher”, in
order to provide reliable andstable control. Therefore, throughout the
teaching process, we assume thatthe operator is skillful andexperienced
enough to master the robot. That is, the trainingdata can fullyreflect the
skills in aparticular robot’s behavior.Besides the qualityofthe training
data,the quantityofthe data points is equally important. If the training
set is in alarger scale, amorecomplete skillcan be described.
4.1
Le
arningb
yC
NN
81
2. Injectivemapping. Another important issue is aboutthe mappingsbe-
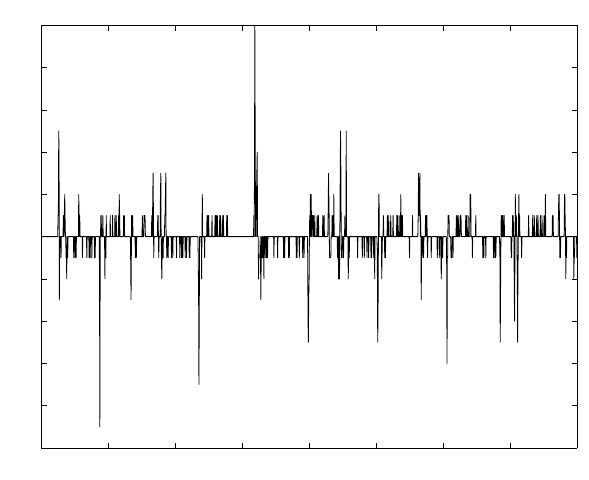
tween inputs andoutputsinastatic map. Figure 4.4 showsahuman
control strategyfor thelateralbalancing behavior,itisnot difficult to fig-
ureo
ut
thatt
he
con
trol
of
thefl
ywheel
is
alw
ay
ss
witc
hi
ng
(a
ve
ry
sha
rp
ch
ange).T
hati
s,
at
as
hort
momen
ta
go,
thec
ommandi
s
po
sitiv
e,
buti
n
the next moment, the command will change to negative.Unfortunately,
the switchingproblemcausesvery similar inputs to be mappedtoradi-
cally different outputs,whichisdifficult for the cascade neuralnetwork
to adaptto, Figure 4.5. To ensure that therewill be acorrectmapping,
enough time-delayedhistories should be provided in the trainingdata
set. In ourcascadenetwork training, we will provide at least 20 piecesof
history data ( n
i
≥ 20) to guaranteethe infectiveness of themapping.
0 5 10 15 20 25 30 35 40
−10
−8
−6
−4
−2
0
2
4
6
8
10
Change of control
time(sec)
Change of control to tilt motor (verticle stabilization)
Fig. 4.4. Switchings in human control of the flywheel.
Foreachmodel, we process the trainingdata as follows:
1. Removal of irrelevantdata
Let[t, t + t
m
]denote an interval of time, in seconds, that ahuman operator
hasgiven an inappropriate command duringthe experiment. Then, we
cut the data correspondingtothe time interval[
t − 1 ,t+ t
m
]fromthe
trainingdata. In other words, we notonly removethe irrelevant data from
the trainingset, butalso the second data leading to the inappropriate
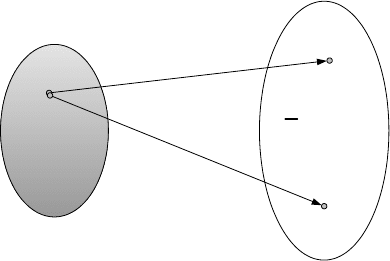
82 4 Learning-based Control
Input space
Output space
()
1 +tu
(
)
,1, -tt
Ξ
...
Γ
Fig. 4.5. Similar inputscan be mapped to extreme differentoutputs if switching
oc
curs.
command time interval. This ensures thatthe cascade model does not
learn controlbehaviors that arepotentially destabilizing.
2. Normalization
We
normalize eac
hi
nput dimensiono
ft
he training data,s
ucht
hata
ll the
input in the trainingd
ata falls insidethe in
terva
l[
− 1 , 1].
3. Generate time-shifteddata
As mentioned in the previous section, we needtoprovide enough time-
delayed values of each state andcontrol variable suchthatthe modelis
able to buildnecessary derivativedependencies between the inputs and
outputs.Inour cascade network training, we will provide 20 pieces of
historydata.
4. Randomization
Finally,werandomize the input-output training vectors andselect half
for training, whilereservingt
he other half fortesting.
Thesampling rate of thetraining data is 40Hz andatypical trainingset
will consist of approximately 10,000 data points.
4.2 Learning by SVM
4.2.1 Support Vector Machines
Support Vector Machine
Originally,SVM wasdeveloped from classificationproblems.Itwas then,ex-
tended to regression estimation problems,i.e., to problems related to findthe
function y = f ( x )given by its measurements
y
i
with noise at some (usually
random) vector x
( y
1
, x
1
) ,..., ( y
l
, x
l
) . (4.15)
