Yangsheng Xu, Yongsheng Ou. Control of Single Wheel Robots

Подождите немного. Документ загружается.

el-based

Con

trol

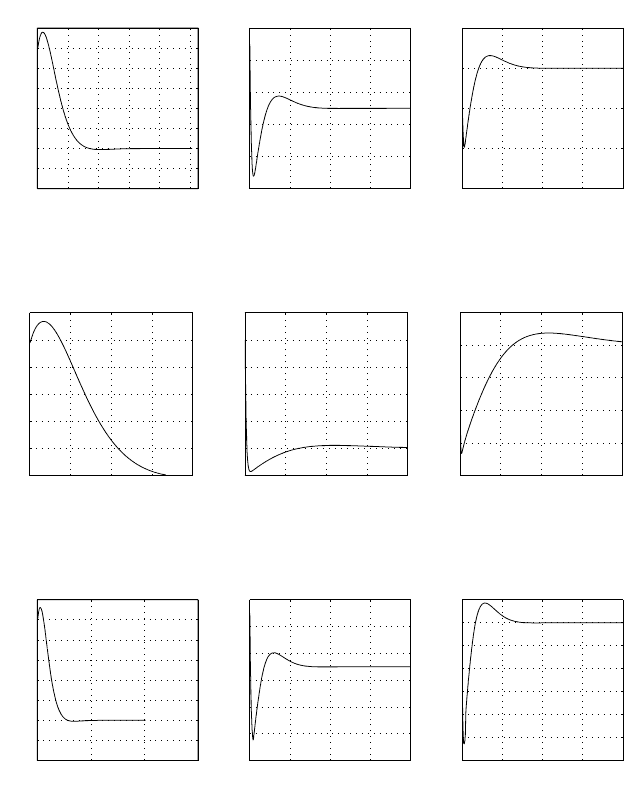
resultsand the initial conditionsare shown in Figures 3.5, 3.6, 3.7 andTa-

ble 3.1, respectively.Inthesesimulations, the rolling speed ˙γ of therobot is

controlled to anominalrollingspeed Ω

◦

=30 rad/s,thusthe contact point

cit

is also aconstant. Thesmoothness is set to 30.

Forsimulation S 1, therobot hasasmaller path curvaturethaninsim-

ulation S 2, because its initial headingangle ϕ (0) in simulation S 1isless

deviatedfromthe Y-axisthaninsimulation S 2. Furthermore, since therobot

hasl

arger

cur

turei

ation

S 2,

resultsi

harp

turns.T

his

end,the robothas to lean steeper to provide asuﬃcient steering velocity˙α in

simulation S 2. Thesituation becomes more serious in simulation S 3. Figure

3.7 shows the leanangle β is saturated in 5sec. Because the initial heading

angle ϕ (0) is more than 90

◦

,inorder to ensure the curvature continuitywhile

ing

the

Y-axis,

should

the

rgest

path

curva

turea

mong

them

suchthatthe lean angle β of therobot is thesteepest, to provide asuﬃcient

steeringvelocity. As we have alreadyset up alimit for the state feedback

controller, the lean anglecan only be stabilized within β ∈ ( − 60

◦

, 60

◦

). Oth-

erwise, the controller will become saturated andthe lean angle will be ﬁxed

at thelimiting value. When the

robot

graduallyapproaches theY-axis, the

leanangle graduallyincreasesuntil it reaches the verticalposition (90

◦

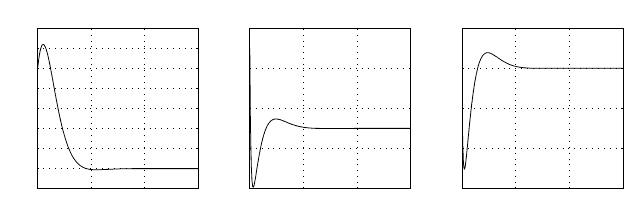
Eﬀectofthe rolling speed

In this section, we studythe eﬀect of therollingspeed of the robot˙γ on

the path following controller.

The sim

ulation results with diﬀerentrolling

speeds areshown in Figures 3.8 and3.9, both with the same initial conditions

as in simu

lation

S 1. Fo

r˙

γ =30 rad/s,t

he robo

onve

rges to the Y-axis

more rapidly than the other one, comparingFigures 3.8a and3.9a.From

Figures 3.8b and3.9b, the change of thelean angle β of therobot with a

lowe

ollings

peed is more signiﬁcantthanthatofthe robotwith ah

igher

rolling speed. It is because, for the robot with agreaterrollingspeed, based

on Eq. (3.16), alesser steering velocit

equired fortracking the same

path

curvature feedback κ .Thus, the change of thelean angle β decreasesaccording

to Eq. (3.9).

3.2 Nonlinear Model

Recently, there has been growing interest in the design of feedback con-

trol laws for nonholonomic systems [57]. Due to Brockett’s theorem in [123], it

is well known that a nonholonomic control system cannot be asymptotically

stabilized to a resting conﬁguration by smooth time-invariant control laws

[18]. Despite this, several discontinuous or time-variant approaches have been

proposed for stabilizing such systems in [18], [46], [57], [63] and [104]. The

references above refer to systems with ﬁrst-order nonholonomic constraints,

3.2

Non

linear

del

0 20 40 60 80 100

−2

−1

(a)

0 5 10 15 20

100

120

140

(b)

0 5 10 15 20

−0.03

−0.02

−0.01

0.01

(c)

β [ deg]

x [ m ]

y [ m ]

Fig.

3.8.

The

lation

results

forf

ollow

ing

theY

-axis

with

γ =1

d/s

0 10 20 30 40

(a)

0 5 10 15 20

100

110

120

130

140

(b)

0 5 10 15 20

−20

−15

−10

−5

x 10

−3

(c)

β [ deg]

x [ m ]

y [ m ]

Fig. 3.9. The simulation results forfollowing theY-axis with ˙

γ =30 rad/s.

0 50 100 150

−2

−1

(a)

0 5 10 15 20

100

120

140

(b)

0 5 10 15 20

−0.03

−0.025

−0.02

−0.015

−0.01

−0.005

0.005

(c)

β [ deg]

x [ m ]

y [ m ]

Fig. 3.10. The simulation results forfollowing theY-axis with σ =20.

whichcan usuallybeexpressed in terms of nonintegrable linear velocityre-

lationships. However, there areanotherkind of mobilerobot systems, which

possess both ﬁrst-order and second-order nonholonomic constraints, such as

ourrobot –Gyrover, bicyclesand motorcycles.Mobilerobots have their in-

herentnonholonomicfeatures, whichcan be describedasﬁrst-order nonholo-

nomicconstraints amongjointvelocities and Cartesian space velocities. These

constraints arise when robotsroll on theground without slipping.Because no

actuators can be useddirectly for stabilizationinthe lateraldirection, these

el-based

Con

trol

0 50 100 150

−1

(a)

0 10 20 30

100

120

140

(b)

0 10 20 30

−15

−10

−5

x 10

−3

(c)

β [ deg]

x [ m ]

y [ m ]

Fig.

3.11.

The

lation

results

forf

ollow

ing

theY

-axis

with

σ =4

systems areunderactuatednonlinearsystems. This induces another nonholo-

nomic constraintofrobots.Thus, to compare with the aboveresearchwork,

our mobilerobot systems–Gyrover, is more challengingtobecontrolled.

This work canprovide some ideas forthatclass of problems. In this thesis,

we want to control an underactuatedmobilerobot system –Gyrover. Thereare

two

con

trol inputs:one is

thesteeringt

orque(

or steering rate)and theother

is thedriving torque (ordriving speed). However, we have four independent

generalizedcoordinatest

ontrol: (1)

thel

ean angle, (2)the heading angle,

(3) theCartesian space X axis, (4) theCartesian space Y axis.

rs [6]a

nd [7]a

ssumed that

the

robot

remained around the vertical

position, whichsimplifythis nonlinearsystem to alinear one. Therefore vali-

dation of theresults can be limited. Some work hadbeen about the tracking

of arollingdisk, suchasin[87], whichassumed three control inputs in the

direction of

steering, leaninga

nd rolling,where no

unactuatedj

ointand no

second-order constrainti

resented.I

34], thea

uthors

impliﬁed the bicycle

dynamic model, andused velocities as control inputs to enable the lean angle

(called “roll-angle” in that paper)

to trackt

rajectories, which

con

tinu-

ousdiﬀerentials. However, the controller couldnot guaranteethatthe bicycle

would nottopple over,i.e. the lean angle wasout of range, before convergence.

In thischapter, we focus on three controlproblems that have notyet been

solved forGyrover. Theﬁrst oneisthe balance of therobot whilestand-

ing. The second one is concerned with point-to-pointcontrol. Thethird one

relatestofollowing astraightline. These three problems are of signiﬁcance

in controlling asystem with both ﬁrst-order and second-order nonholonomic

constraints.

InertiaMatrix and Nonholonomic Constraints

Thekinematics anddynamics of Gyrover are diﬀerent fromthose of unicycles,

suchasin[1]. Thediﬀerence lies in the assumption that the unicycle always

remainsvertical. On the contrary,Gyrovercan be considered as arollingdisk

whichisnot constrainedtothe verticalposition and is connected to ahigh

3.2

Non

linear

del

speed spinning ﬂywheel. This modelcan servewell as asimpliﬁcation for the

study of amodel of Gyrover.

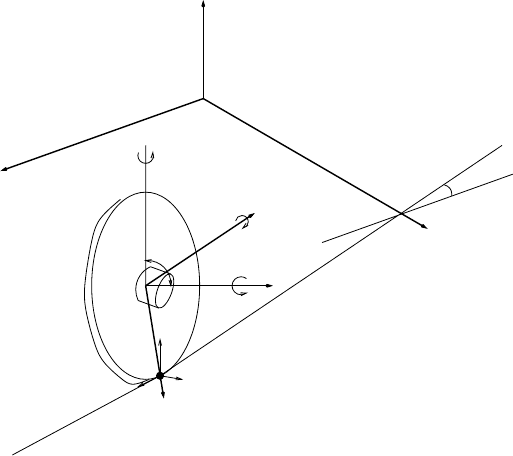
Consider adisk rolling without slipping on ahorizontal planeasshown in

Figure

4.9.

Let



X, Y, Z and



x, y, z be the inertial frame whose x − y

plane is anchored to theﬂat surface andthe body coordinate frame whose

origin is locatedatthe center of therollingdisk, respectively.Let ( X, Y,Z )be

the Cartesian coordinates of thecenter of mass(c )with respect to the inertial

frame



.Let A denote the pointofcontactonthe disk. The conﬁguration

of thedisk canbedescribed by six generalizedcoordinates(X, Y,Z, α, β,γ ),

where α is the steering (precession) anglemeasured from X -axis to the contact

line, β ∈ (0,π)isthe lean (nutation)angle measured from Z -axis to the z ,and

γ is the rolling angle. R is the radius of Gyrover. m, I

and I

represent

the total mass and the momentofinertia of Gyrover.

Fig. 3.12. System parametersofGyrover’s simpliﬁed model.

In thederivationofthe model,weassume that the wheel rolls on the

groundwithout slipping. Based on the previous derivation in [112]and letting

:= sin ( x ), C

:= cos ( x ), the dynamic model is

M ( q )¨q = N ( q, ˙q )+Bu (3.29)



X = R (˙γC

+˙αC

−

βS

)

Y = R (˙γS

+˙αS

βC

)

(3.30)

el-based

Con

trol

where q =[α, β, γ ] ,N =[N,N,N ]

123

M =





0 M





B =



100

001



,u=





= I

+ mR

) C

=(2 I

+ mR

) C

= I

+ mR

= M

=2I

+ mR

=(I

+ mR

) S

2 β

˙α

β +2I

β ˙γ

= − mgRC

− ( I

+ mR

) C

˙α

− (2I

+ mR

) S

˙α ˙γ

=2( I

+ mR

) S

˙α

β,

where(X , Y , Z )i

he robo

t’s center of

massc

rdinate with

respect to the

inertial frame as shown in Figure4.9. M ( q ) ∈ R

3 × 3

and N ( q, ˙q ) ∈ R

3 × 1

are

the inertial matrix andnonlinearterms, respectively.Equations (3.29) and

(3.30) form the dynamic model andﬁrst-order nonholonomicconstraints in

the form of

velocit

In order to simplify the control design, we will transform the inertia matrix

of them

el to ad

iagonal matrix and reduce the

nonlinear terms

of the

dynamicmodel. We ﬁrstintend to cancel some nonlinear terms by letting



= − N

+ u

= − N

+ u

(3.31)

Substituting Equation (3.31) into Equation (3.29) yields







¨α + M

¨γ = u

β = − mgRC

− ( I

+ mR

) C

˙α

− (2I

+ mR

) S

˙α ˙γ

¨α + M

¨γ = u

(3.32)

om theﬁ

rst andthird equations in Equation (3.32) solving withr

espect to

¨α and¨γ oneo

btains

= M

− M

Due to its “shell” structure, even when Gyrover topplesover, thelean angle

is not zero, so that S

> 0and M

> 0for all t .Then, we let



=(M

) u

− ( M

) u

= − ( M

) u

+(M

) u

andobtain

3.2

Non

linear

del







¨α = u

β = − mgRC

− ( I

+ mR

) C

˙α

− (2I

+ mR

) S

˙α ˙γ

¨γ = u

(3.33)

Equation (3.30) is nonintegrable, whichisdeﬁned in [86]. Hence, it is the

ﬁrst-order nonholonomicconstraintofthe robotsystem. Moreover,wenote

that no controlinput is available foractuatingdirectly on leanangle β .This

forms

onstrain

celerations.

Orio

80]

pro

sed

some necessary conditions forthe partial integrabilityofsecond-order non-

holonomic constraints, oneofthe conditions is that thegravitational term G

is constant. In Equation(3.33),the gravitational term variesalong β ,thusit

is anonintegrable,second-order nonholonomic constraint.

3.2.1Balance Control

Problem Statement

Our ﬁrstcontrol problemistoenable therobot to standvertically,i.e., to

stabilize the

leanangle

β to π/2and

β ,

β ,˙α and˙γ to zero.

Based on theprevious consideration,weare nowable to specifymore

clearly the

aforementioned closed loop steeringp

robleminthe following gen-

eral terms.

Let the robotsystem deﬁned in Equation(3.33) be initially moving in

an undesired state

and assume all the

essentials

tate va

riablesa

re directly

measurable.Then ﬁnd asuitable (ifany)state dependentcontrol law[u

]

whichguarantees the states [ β − π/2 ,

β,

β, ˙α, ˙γ ]tobeasymptotically driven

to the null limiting point[0

, 0 , 0 , 0 , 0]

hilea

voidingany

attainmentofthe

conditions of β =0(or β = π )inany ﬁnitetime.

Balance Control

First, we

let







= mgR/M

=(I

+ mR

) /M

=(2 I

+ mR

) /M

(3.34)

where G

, I

and J

arepositive scalarconstant.

Then,the dynamicequations become







¨α = u

β = − G

− I

˙α

− J

˙α ˙γ

¨γ = u

(3.35)

Letting x

( i )

be the i

time derivativeof x ,then fromEquation(3.35),we

have

(3)

= h

( t )

β + h

( t ) u

+ h

( t ) u

(3.36)

el-based

Con

trol

where







( t )=G

− I

2 β

˙α

− J

˙α ˙γ

( t )=− I

2 β

˙α − J

˙γ

( t )=− J

˙α.

Set β (0) − π/2=a,

β (0)

c ,a

eal

σ be

σ = | 3 a +2b + c | / 2+| a +2b + c | / 2+| a + b | /

√

2 .

Proposition 1 Consider the system (3.35) with the feedbackcontrol laws

and u



− (˙α −

√

V )i

f˙

α (0) > 0

− (˙α +

√

V )otherwise

(3.37)

where V is deﬁned in Equation(3.39) and k

is apositive number,whichcan

be designed, and

= − (3(β − π/2) +5

β +3

β + h

( t )

β + h

( t ) u

) /h

( t )(3.38)

where, h

( t ) ,h

( t )are deﬁnedasinEquation (3.36).

Anys

tate (˙

α, ˙γ,β,

β,

β )s

tarting fromt

he domain

D ,w

hichisdeﬁned as

D = { (˙α (0), ˙γ (0),β(0),

β (0),

β (0))| ˙α (0) =0,

0 <β(0) <π,σ<π/ 2 , ˙α, ˙γ, β,

β,

β ∈ R

}

converges to thelimiting point[0 , 0 ,π/ 2 , 0 , 0]

To presentthe proof,weneed alemma.

Lemma 1:

Consider amechanical system with aconstraintamong anumberofstates

( t ) ,x

( t ) ,..., x

( t ) ∈ R

ne of theses

tate va

riablesi

suniquelyd

etermined

by the other states; i.e., x

= f ( x

,...x

n − 1

). Let the limit of x

exist as

t →∞anda

ll the other statesb

easymptotically stabilizable to some real

values. If allofthe statesare continuousand bounded, forall of t ,then, x

is also asymptotically stabilized to its limit, whichisdecided by theother

states.

Proof:

First, since x

( t )iscontinuousand bounded, forall t, it is stable.

Second,because allofthe other statesare asymptotically stabilized to

some values, thus

lim

t →∞

= e

exist i =1, 2 ,..., n − 1 .

Moreover, accordingtothe propertyoflimits, we have

lim

t →∞

=lim

t →∞

f ( x

,...x

n − 1

) ,

lim

t →∞

= f (lim

t →∞

, lim

t →∞

,..., lim

t →∞

n − 1

) .

3.2

Non

linear

del

Because x

is uniquely decided by theother states andhas alimit as time

goes to inﬁnity, x

will convergetothe limitdecided by theother states.

Then,weaddressthe proof for Proposition 1 .

First, to prove thesubsystem β,

β,

β asymptoticallystabilized, we consider

the

llow

ing

apunov

func

tion

candidate

V =(β − π/2)

/ 2+(

β + β − π/2)

/ 2+(

β +2

(

β + β − π/2))

/ 2 . (3.39)

We needtosolvetwo more problems before we can prove the subsystem is

asymptoticallystable. Oneiswhether ˙α is not zero in anyﬁnitetime; the

other is whether the controllers guarantee β is constrained in (0,π). We will

addressthe ﬁrst problemlater. We prove the second problem by replacing u

into Equation(3.35).Wehave

(3)

= − (3(β − π/2) +5

β +3

β ) . (3.40)

By solvingthis lineardiﬀerential equation, we obtain

β − π/2=e

− t

((3a +2b + c )+

√

2(a + b )sin

(

√

2 t ) − ( a +2b + c )cos

(

√

2 t ))/ 2 .

From σ<π/2, we

knowthat0

<β<πfora

ll t.

Then,fromEquation (3.39)the time derivativeof V is

V =(β − π/2) +(

β + β − π/2)(

β +

β )+(

β +2(

β + β − π/2))( β

(3)

+2(

β +

β )).

By substitutingEquation (3.40)intoit, we have

V =(β − π/2)+(

β + β − π/2)(

β +

β ) − (

β +2(

β + β − π/2))(3

β +3

β +3( β − π/2)).

Then,

V = − ( β − π/2)

− (

β + β − π/2)

− (

β +2(

β + β − π/2))

. (3.41)

We can usethe following Lyapunov function to prove˙α converging to zero.



V/4+ ˙α

/ 2 .

om Equations(3.39) and(

3.41),w

V = − 2 V. (3.42)

Thetime derivativeof V

√

+˙αu

By substitutingEquations (3.42) and (3.37)intoit,

el-based

Con

trol

= −



V/4 − (˙α ∓



V )˙α.

Then,

= − (



V/2 ∓ ˙α )

. (3.43)

Then

pro

ondition˙

α =0

can

pproac

hed

ﬁnitetime. Without losing generality, we assume ˙α (0) > 0and let k

be 1.

If we let V (0) = V

,fromEquation (3.42), andbysolvingthe diﬀerential

equation, we obtain

V = e

− 2 t

putting

Equation(

3.37),w

¨α = − (˙α − e

− t/2



) .

By solving this diﬀerential equation, we obtain

˙α = e

− t

˙α (0) +2(

− t/2

− e

− t

)



Thus, since ˙α (0) > 0, ˙α can notreachzero in anyﬁnitetime.

Sinces

β and˙α aren

ot zero in

yﬁnitetime, then

( t )doe

snot

become zero forall t andfromEquation (3.44), ˙γ is continuous.Wewill prove

that the limit of ˙γ exists and is zero, as time goes to inﬁnity.

From Lemma1,ifweasymptotically stabilize

β,β, ˙α andguarantee that

all of these states are continuous andbounded ,˙γ will asymptotically converge

to zero. Since ˙

α will never

zero, therea

re two

problems left.

Onei

hether

β,

β can be stabilized andthe other is whether we can guarantee 0 <β<π

fora

ll of

t .F

romEquation (3.35), we

ve,

˙γ =

β + G

+ I

˙α

− J

˙α

. (3.44)

As V and˙α reach

very small va

lues,

√

V is the higher order small of

√

V .

For | β − π/2 |≤

√

V , | β − π/2 | is the higher order small of

α ,and

and

β .Using aTaylor series expansion, cos(β )isahigher order small of ˙α .

Thus, fromLemma 1and the aboveequation, ˙γ asymptoticallyconverges to

zero.

3.2.2 PositionControl

Here, we propose acontroller that drivesthe robottothe Cartesian space ori-

gin to studythe pointtopoint control problem. Thisisextremely important,

foritserves as thebasisfor Cartesian space tracking.

Since the originofthe frame XY ZO(



o )inFigure 4.9isﬁxed on the

ground, forthe purposes of trackingproblems,itismoredirect to use the point

of contactAon theground to describe the position of therobot, instead of

thecenter of mass. Let ( x

)bethe coordinatesofthe contact pointAon

3.2

Non

linear

del

the ground thatcoincides withapointofcontactPofthe robotinFigure 4.9.

and y

can be expressedas







X − RS

Y − RC



(3.45)

DiﬀerentiatingEquation (3.45)with respect to time, we obtain,



˙x

= R ˙γC

˙y

= R ˙γS

(3.46)

Thereare two kinds of input controlcommands forGyrover: oneset of con-

trol commandsare torques and theother set of commands are velocities. The

velocitycommands u

and u

control ˙α and˙γ ,respectively.Thus, Equations

(3.30) and (3.33) transform into











˙α = u

β = − G

− I

− J

˙γ = u

˙x

= Ru

˙y

= Ru

(3.47)

where G I and J are the same as in Equation (3.34).

Problem Statement

Let us consider the robot with respect to the inertial frame XY Z O (



o ),

as shown in Figure 3.13. By representing the Cartesian position of the robot

in terms of its polar coordinates, which involves the error distance e ≥ 0,

Fig. 3.13. Parameters in position control.