Yangsheng Xu, Yongsheng Ou. Control of Single Wheel Robots
Подождите немного. Документ загружается.


32
2K
inematicsa
nd
Dynamics
0 0.2 0.4 0.6 0.8
0
0.2
0.4
0.6
0.8
0 0.2 0.4 0.6 0.8
0
2
4
6
8
10
0 0.02 0.04 0.06 0.08 0.1 0.12 0.14
−0.45
−0.4
−0.35
−0.3
−0.25
−0.2
−0.15
−0.1
−0.05
0
0 1 2
0
0.5
1
1.5
2
t
α (in deg)
0 1 2
90
91
92
93
94
95
96
t
β
0 1 2
−1
0
1
2
3
4
t
β
a
0 1 2
−6
−4
−2
0
2
4
6
t
α
.
0 1 2
−2
−1.5
−1
−0.5
0
0.5
t
β
.
0 1 2
0
5
10
15
20
t
γ
.
−0.05 0 0.05 0.1 0.15
−7
−6
−5
−4
−3
−2
−1
0
x
y
path of C.M. of robot on slope
0 0.5 1 1.5 2
−50
0
50
100
150
200
t
τ
angle= 10
o
Fig. 2.13. Rolling down of asingle wheelrobot
Fig. 2.12. Continued

3
Model-based Control
3.1 Linearized Model
3.1.1 Stabilization
Due to
the
inherentlaterali
nstability,
the firsts
tep in
controlling therobot
is stabilization. Fortunately,the lean angle of therobot can be controlled in-
directly by
tilting the
flywheel. The
single wheel robot
steers
by
leaningat
different angles. Therefore, it is necessary to design acontroller that stabilizes
the robotatany desired lean angle, so as to control the steeringvelocity.
On the other hand, fora
ty
pical unicycle,itshould be
notedt
hatt
he lon-
gitudinaland lateralmotionsare highly coupled to eachother,and it is not
suitable to decompose the
motions througha
linearizationmethod(Nakaj
ima
et al. [75]and Sheng [96]).However, because of thestabilizing effect of the
flywheel, the effect of coupling/cross terms between the longitudinal andlat-
eral motionso
ft
he robo
tb
ecome less significantfor thesingle wheel robot.
It is feasible to decouple them
by
linearizingthe dynamicmodel, and then
by designing alinear state feedbacklaw to control thelean angleand rolling
speed of the robot.
LinearizedModel
We
first linearizethe system Eq. (2.32) aboutt
he ve
rticalp
osition. The
defi-
nitionofvariables andthe configuration of thelinearized model areshown in
Table 2.1and Figure 3.1respectively.Inderivation of the linearized model,
we makethe folllowing assumptions: (1)the spinning rate ˙
γ
a
is sufficiently
large andremains constant, so that the terms ˙γ
a
˙
β, ˙γ
a
˙α aresufficiently larger
than the terms
˙
β ˙γ,
˙
β ˙α, ˙α
2
.(2) theterms
˙
δ
β
,
˙
δ
β
a
, ˙α,
˙
θ aresufficiently small, (3)
β =90
o
+ δ
β
, ˙γ = Ω
o
+ Ω, β
a
= δ
β
a
.The linearized model can be represented
as
Y. Xu and Y. Ou: Control of Single Wheel Robots, STAR 20, pp. 33–71, 2005.
© Springer-Verlag Berlin Heidelberg 2005
34
3M
od
el-based
Con
trol
W
A
δ
β
δ
β
β
δ
β
a
D
x
B
z
a
β
a
z
B
tire
plastic
dome
flywheel
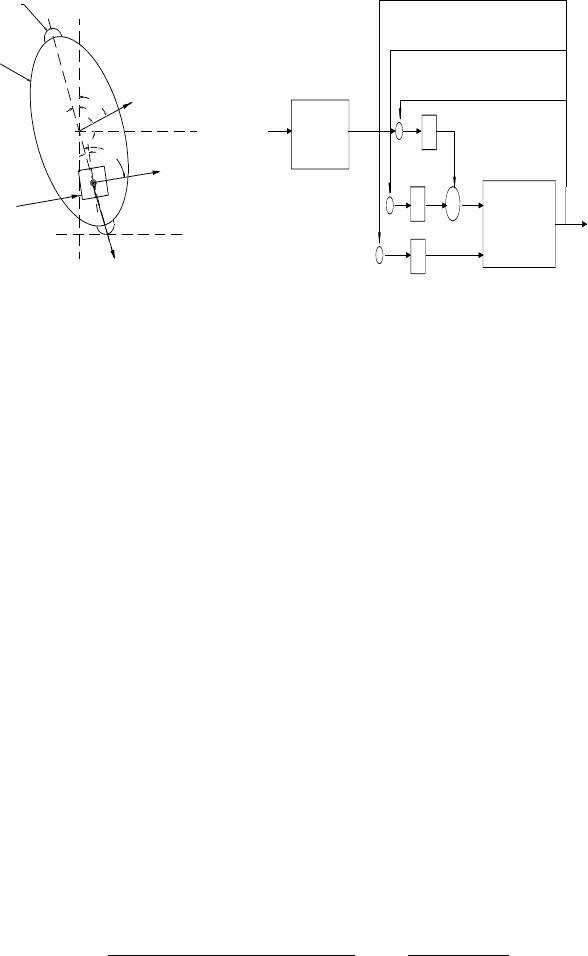
Fig. 3.1. The lateral description of Gy-
rover.
+
+
-
-
--
Eq. (3. 9) k
1
k
2
k
3
u
β
a
u
1
Ω
β
˙
β
qRobot
β
re
f
˙α
re
f
Fig. 3.2. Schematicofthe control algo-
rithms.
( I
xxf
+ I
xxw
)¨α =2( I
xxw
Ω
o
+ I
xf
˙γ
a
)
˙
δ
β
− µ
s
˙α +2I
xxf
˙γ
a
u
β
a
(3.1)
( I
xxw
+ mR
2
)
¨
δ
β
= gmRδ
β
− (2I
xxw
+ mR
2
) Ω
o
˙α − 2 I
xxf
˙γ
a
˙α (3.2)
(2I
xxw
+ mR
2
)
˙
Ω = − µ
g
Ω + u
1
(3.3)
Because Ω is independentofthe roll andy
aw
dynamics (Eqs.
(3.1)a
nd (3.2)),
we
can decompose the
longitudinal motion Eq. (3.3), and establish closed-loop
control forcontrollingthe angular velocity˙γ to the nominal value Ω
◦
.The
remaining ya
wand roll dynamics form astate equation,
˙x = Ax + Gu, (3.4)
where x =
δ
β
, ˙α,
˙
δ
β
T
,
A =
001
0 a
22
a
23
a
31
a
32
0
,G=
0
b
2
0
where a
22
,..., a
32
and b
2
arederived from Eqs. (3.1)and (3.2).
Let C ( A, G )bethe controllabilitymatrix of thesystem Eq. (3.4). Then
|C( A, G ) | = | [ G | AG | A
2
G ] |
= a
2
32
b
3
2
=(
(2I
xxw
+ mR
2
) Ω
o
+2I
xxf
˙γ
a
I
xxw
+ mR
2
)
2
× (
2 I
xxf
˙γ
a
I
xxf
+ I
xxw
)
3
(3.5)
From Eq. (3.5), the system is controllable if ˙
γ
a
=0,for thereasonthatifthe
spinningrate of theflywheel is equal to zero, the flywheel does not provide
an additional force forbalancing therobot.

3.1
Lin
earizedM
od
el
35
If we consider the steering velocity˙α as theoutput of Eq. (3.4), thenthe
transfer function becomes
H ( s )=c ( sI − A )
− 1
b
=
b
2
( − a
31
+ s
2
)
s
3
− a
22
s
2
− ( a
31
+ a
23
a
32
) s + a
22
a
31
(3.6)
where c =[0 , 1 , 0] and b = G =[0 ,b
2
, 0]
T
.N
ote
th
at
th
erei
sa
zero
of
H ( s )
on theright-half plane, thereforeitisanon-minimum phase. This means that
the robotwill fall if we control the steering rate ˙α only.
Linear State Feedback
Based on the system Eq. (3.4), if we stabilize the robot to adesired lean angle
δ
βref
such
that
δ
β
= δ
βref
, ˙α =˙α
s
,
˙
δ
β
=0rad/s,
¨
δ
β
=¨α =
˙
Ω =0rad/s
2
, (3.7)
then the linear state
feedbackcan be
designed as
u
β
a
= − k
1
( δ
β
− δ
βref
) − k
2
˙
δ
β
− k
3
(˙α − ˙α
s
) . (3.8)
where k
1
,k
2
, and k
3
aref
eedbackgainsand ˙
α
s
is the equilibriumsteeringr
ate
under theconditions Eq. (3.7), thatis
˙α
s
=
gmRδ
βref
(2I
xxw
+ mR
2
) Ω
o
+2I
xxf
˙γ
a
(3.9)
In order to
ensure an
asymptotic stabilityo
ft
he system Eq. (3.4), the neces-
sary conditions of thefeedbackgainsare
k
1
< 0 ,k
2
< 0 ,k
3
> 0 .
Asymptotic stabilityensuresthatall eigenvalues of the closed loop system
have negative real parts. Note that forthe givennominalrollingspeed Ω
◦
,
the equilibriumsteeringrate ˙α
s
corresponds to one, and only onelean angle
δ
βref
.Thu
s
δ
βref
and ˙α
s
can notb
eselected independently
.
To allow therobot to trackadesired path on the ground, we must be able
to control itssteeringand linearvelocities. Fortracking the desired steering
velocity˙
α
ref
,wepropose to trackaroll angle δ
βref
in whichthe equilib-
rium steering velocity˙α
s
will be equal to the desired one˙
α
ref
,accordingto
Eq. (3.9). The schematicdiagram for controlling thesteeringrate is shown in
Figure3.2.
36
3M
od
el-based
Con
trol
3.1.2Path FollowingControl
The kinematic constraints of atypical mobile robot with asteeringfront wheel
canbewrittenas
˙x
˙y
˙
θ
=
cos θ 0
sin θ 0
01
υ
ω
(3.10)
where(x,
y
)i
st
he
po
sition
of
the
cen
ter
of
th
ev
eh
icles,
θ is
the
or
ien
tation,
and ( υ, ω )are the linearand steering velocities of thetypical mobile robot
respectively.Anumberoftrajectory trackingmethods have been proposed
for the typical mobilerobot [58],[87], [49],[89], [99].However, because the
single wheel robot is notassumed to be in avertical position, the constraints
described in Eq. (3.10) also depend on the leanangle andlean rate in this
case. Furthermore, forthe typical mobilerobot, thesteeringvelocity ω can be
directly generatedbyturning the front wheel. The single wheel robot steers by
leaning itself to apredefined angle. Therefore, the main difficultyinsolving
the path following problem of
thesingle wheel robot
is
that
we
must not
only control thep
osition (
x, y )a
nd the orientation
θ using two
control
inputs
( υ, ω ), butalso control the lean angle β within astableregiontoprevent the
robo
tf
romf
alling.
Here, we propose an approach to thepath following problem based on a
geometrical notion in
controlling thepath curvature. We
redefine the system
configuration of
therobot
based on the geometrical notion and characteristics
of thenonholonomicmotion.
Robot
Configuration
In theprevious sections, we considered thecenter of mass(X
c
,Y
c
)tobethe
position of the robot. However, forpath following wherethe robotneeds to
tracka
desiredp
ath on
theground, it is be
tter to
usethe pointofcontact
a
on theground to describe the position of therobot, instead of thecenter of
mass C (Figure 2.1).Let ( x
a
,y
a
)bethe coordinatesofthe contact point a on
the locus that coincides with apoint of contact p of therobot. x
a
and y
a
can
be expressed as
x
a
y
a
=
X
c
− RS
α
C
β
Y
c
+ RC
α
C
β
(3.11)
DifferentiatingEq. (3.11) with respect to time, velocityconstraints at the
contact point
a arefound to be
˙x
a
˙y
a
=
υ
a
C
α
υ
a
S
α
(3.12)
where υ
a
is the contact pointvelocity,
υ
a
= R ˙γ (3.13)

3.1
Lin
earizedM
od
el
37
Note that Eq. (3.12) is independentofthe lean angle β andisidentical to the
rolling constraints of atypical mobile robot,i.e. thereisnodrift terminEq.
(3.12).
The
status
of
th
ec
on
tac
tp
oin
to
ft
he
ro
b
ot
can
be
de
scrib
ed
by
an
alter-
native
set
of
co
nfigurationsb
asedu
po
n[
48],
q =(p, ϕ, κ )=(( x
a
,y
a
) ,ϕ,κ) , (3.14)
where(x
a
,y
a
), ϕ and κ arethe position, the headingorientation andthe path
curvatureofthe robotwith respect to the inertial frame, respectively.The new
configuration of therobot is showninFigure 3.3.The heading orientation ϕ
is
measured
ab
out
the
X-axis
while
the
ya
wa
ngle
α is
measured
ab
out
the
Y-axis. Then
ϕ = α −
π
2
, ˙ϕ =˙α. (3.15)
Normally,wecontrol thekinematic system of the robotusing the steering
andlinear velocities to trackadesired path.However, we can onlyindirectly
cont
rolt
he steering velocit
yo
fa
robo
tb
yc
hanging its
lean angle. Because the
motionofthe contact point a undergoesnonholonomicmotion [48],its path
curvature κ can be
expresseda
s,
κ ( t )=
dϕ( t )
ds
=
˙ϕ ( t )
υ
a
( t )
=
˙α ( t )
υ
a
( t )
=
1
r ( t )
(3.16)
where r ( t ), s and˙ϕ ( t )a
re the radius of
thecurvature fromt
he center of
ro-
tation c to the contact po
int
a ,t
he path length, andthe rotational velocit
y
of therobot, respectively (Figure3.3). If the center c of therotation is at
infinity,
therobot
is
mo
ving in
astraightline andthe path curvature and
steeringvelocityare zero.FromEq. (3.16), forthe givenlinear velocity υ
a
,we
can controlthe path curvature κ by controlling the steeringvelocity˙α .
Line Following
We designed aline following controller forthe robottotrack adesired straight
line. It is divided into two parts:(1) thevelocitycontrol lawand (2) thetorque
control law. Using the velocitycontrol law, thevelocityinputs of therobot
can be designed based on the error between the currentconfigurationsofthe
robotand the giventrajectory.Assumingthatthe linearvelocityofthe robot
is fixed/controlled to anominalvalue, we consider thesteeringvelocityasthe
only velocityinput forthe robot. Using the torquecontrol law, we can design
the tilt torque of the flywheel in order to leanthe robottoapredefined angle
whichcorresponds to the velocityinput (steering velocity) obtained from the
velocitycontrol law.

38
3M
od
el-based
Con
trol
desired
line
Robot
d
δ
d
ϕ
1
a
X
Y
trajectory
− x
a
y
a
r ( t )
ϕ
L
α
˙α
c
Fig. 3.3. Principleofline following.(topview)
Eq. (3. 9)
δ
βref
κ
dκ
ds
dκ
ds
= − aκ − bϕ − cx
a
˙q
q
Dynamics
Kinematicsu
β
a
= − k
1
( δ
β
− δ
βref
)
− k
2
˙
δ
β
− k
3
(˙α − ˙α
ref
)
˙α = κυ
a
˙α
ref
u
β
a
x
a
,y
a
Torquecontrol law
Velocitycontrol law
Fig. 3.4. Schematico
fthe control algorithm for the Y-axis.
Velocitycontrol law
Unlikesome typical control methodsfor thenonholonomicsystem, we used
the path curva
tureasav
ariable to
describet
he path tracking of the robotwith
nonholonomicc
onstraints.T
herefore, basedon[48], we
consider thederiva-
tiveofthe path curvature as thevelocitycontrol lawand thenexpress the
derivativeofthe path curvature (
dκ
ds
)with respect to the path length sas:
dκ
ds
= − aκ − b ( ϕ − ϕ
1
) − cδ
d
, (3.17)
where a , b and c arepositive constants, ϕ
1
and δ
d
arethe directionofthe
desired line andthe perpendiculardistance between the robotand thedesired
line respectively (Figure3.3). Eq. (3.17) is called asteeringfunction. If (
a, b, c )
areselected suchthatEq. (3.17) is asymptotically stable, the continuityof
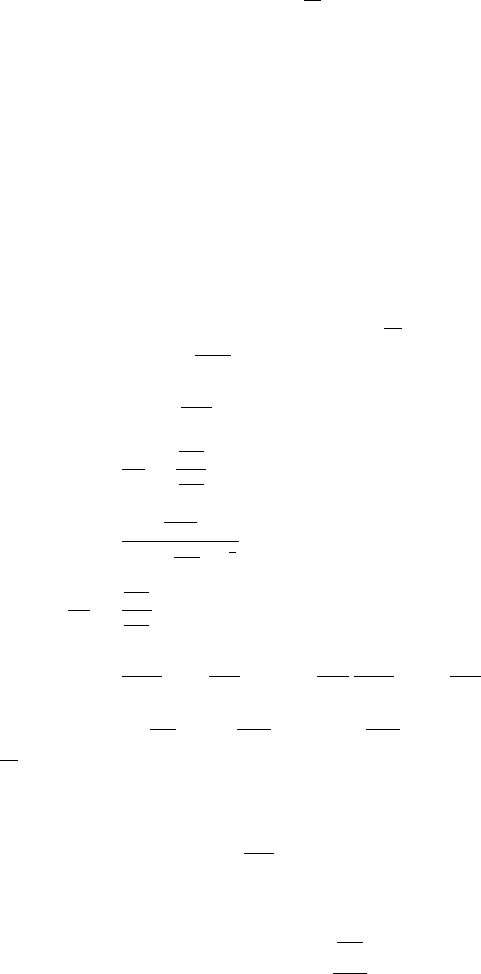
3.1
Lin
earizedM
od
el
39
thepath curvature canbeensured, and
dκ
ds
→ 0asthe path length s increases,
i.e., δ
d
→ 0, κ → 0and ϕ → ϕ
1
as s increases. Hence, the robotconverges to
thedesired straightline asymptotically.Inorder to designthe velocityinput
(steering
ve
lo
cit
y),
we
firs
tfi
nd
the
pa
th
cu
rv
a
tiv
ef
eedbac
k
κ by
in
tegrating
the Eq. (3.17) in eachinstant. Usingthe givenlinear velocityand the path
curv
ature
fee
dback
,w
ec
an
obtaint
he
corr
esp
ondingv
e
lo
cit
yi
nput
fo
rt
he
robotaccordingtoEq. (3.16).
Convergence of the velocitycontrol law
To achieve convergenceofthe control lawEq. (3.17), we must select aproper
set
of
co
efficien
ts
(
a,
b,
c
).
We
first
transform
th
ec
oo
rdinate
system
suc
ht
hat
the desired path becomes the Y-axis, i.e., δ
d
= − x
a
,ϕ
1
=0
.T
hen
we
in
tr
od
uce
anew time scale whichisidenticaltothe distance alongthe desiredpath y
a
andrepresentvariables in Eq. (3.17) ( x
a
,ϕ,κand
dκ
ds
)interms of the derivative
of x
a
with respect to y
a
.(
d
n
x
a
dy
n
a
)
ϕ = tan
− 1
(
dx
a
dy
a
)(3.18)
κ =
dϕ
ds
=
dϕ
dy
a
ds
dy
a
=
d
2
x
a
dy
2
a
(1 +(
dx
a
y
a
)
2
)
3
2
(3.19)
dκ
ds
=
dκ
dy
a
ds
dy
a
,
=
d
3
x
a
dy
3
a
(1 +
dx
a
dy
a
2
)
− 2
− 3
dx
a
dy
a
d
2
x
a
dy
2
a
2
(1 +
dx
a
dy
a
2
)
− 3
(3.20)
Note that if
x
a
→ 0,
dx
a
dy
a
→ 0,
d
2
x
a
dy
2
a
→ 0and
d
3
x
a
dy
3
a
→ 0, then ϕ → 0, κ → 0
and
dκ
ds
→ 0. Hence,the robotconverges to
theY-axis. In
order to track
the
Y-axis, x
a
andits derivativewith respect to y
a
must convergetozero. To this
end, we define asystem of the firstorder equation,
dξ
dy
a
= f ( ξ ) , (3.21)
where
ξ ≡
ξ
1
ξ
2
ξ
3
≡
x
a
dx
a
dy
a
d
2
x
a
dy
2
a
(3.22)
If thesystem of Eq. (3.21) is asymptotically stable,
x
a
andits derivativewith
respect to y
a
convergetozero asymptotically.Using the Jacobian linearization,
the system of Eq. (3.21) becomes

40
3M
od
el-based
Con
trol
dξ
dy
a
= Aξ
,
(3.23)
where
A =
df
dξ
ξ =0
=
01
0
00
1
− c − b − a
(3.24)
To ensure the asymptotic stabilityofthe system Eq. (3.23), a, b and c must be
larger than zero while ab >c.The solutionfor criticallydamped conditions
is,
a =3k, b =3k
2
,c= k
3
. (3.25)
where k is the gain of thevelocitycontrol law.
σ =
1
k
(3.26)
where σ is called the smoothnessofthe velocitycontrol law.
To
rque cont
rol la
w
By the velocitycontrol law, thesteeringvelocityinput is definedwhen the
linear velocityisgiven. Because of theabsence of thefront steeringwheel, the
robo
ts
teers only by
leaningitself to ap
redefined angle. Therefore, we
propo
se
to design the tilt input of theflywheel u
β
a
fort
rack
ing alean angle tra
jectory
δ
β
( t )thatiscorresponding to the givensteeringvelocity. Assumingthatwe
can controlthe lean angle β faster thanthe control of thesteeringvelocity˙α ,
we ma
yc
on
sid
er
˙
α to be
fixedinthe
β time scale.
Based on Eq. (3.9), we can controlthe steering velocity˙α to the desired
va
lue wherethe robotm
ustb
estabilized to the corresponding lean angle
δ
βref
.
The linear state feedbackfor stabilizingthe robottothe desiredlean angleis
u
β
a
= − k
1
( δ
β
− δ
βref
( t )) − k
2
˙
δ
β
(3.27)
where δ
β
and δ
βref
are thesmall pertubation of thelean anglefromthe ver-
tical position andthe referencelean angle respectively.Note that thesteering
velocity˙α does notappearinEq. (3.27) because if the robot stabilizes to
the desired lean angle δ
βref
,i
ts steeringr
ate must conv
erge to
an
equilibrium
value accordingtoEq. (3.9). Therefore, thereisnoneed to include the steer-
ing velocityinthe state feedbackEq. (3.27). The overall architectureofthe
control algorithm has been shown in Figure3.4.
3.1.3 Control Simulation
We first showthe simulationresults of the robottotrack adesired line y =
tan 30
◦
x ,with
3.1
Lin
earizedM
od
el
41
ϕ
1
=
π
6
,δ
d
=
x
a
− tan 30
◦
y
a
sec
30
◦
. (3.28)
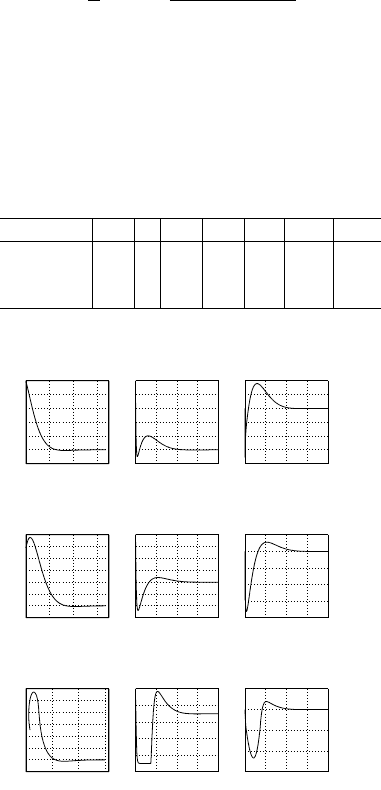
Thesimulation results are showninFigure 3.5.The initial conditions in this
sim
ul
ation
ares
ho
wn
in
Ta
ble
3.
1.
Th
ed
ecoupled
dynamic
mo
de
l[
124]
is
adopted through out the simulations.
Sim
ula
tion
X
a
Y
a
α (0) β (0) κ (0) β
a
(0) ϕ (0)
S 1 5[m ] 0 70
◦
110
◦
0 0 − 20
◦
S 2
5[m ] 0 110
◦
130
◦
0 0 20
◦
S 3 5[m ] 0 210
◦
110
◦
0 0 120
◦
Table 3.1. Theinitial conditions for the simulations with differentinitial heading
angles
0 20 40 60
−1
0
1
2
3
4
5
(a)
0 5 10 15 20
85
90
95
100
105
110
115
(b)
0 5 10 15 20
−8
−6
−4
−2
0
2
4
x 10
−3
(c)
β [ deg]
x [ m ]
y [ m ]
tt
κ
Fig. 3.5. The simulation results (
S 1) for following theY-axis.
0 20 40 60
−1
0
1
2
3
4
5
6
(a)
0 5 10 15 20
60
70
80
90
100
110
120
130
(b)
0 5 10 15 20
−20
−15
−10
−5
0
5
x 10
−3
(c)
β [ deg]
x [ m ]
y [ m ]
tt
κ
Fig. 3.6. The simulation results (
S 2) for following theY-axis.
−3 17 37 57
−2
0
2
4
6
8
10
12
(a)
0 5 10 15 20
20
40
60
80
100
120
(b)
0 5 10 15 20
−0.15
−0.1
−0.05
0
0.05
(c)
β [ deg]
x [ m ]
y [ m ]
tt
κ
Fig. 3.7. The simulation results ( S 3) for following theY-axis.
Figure3.5 showsthatthe robottracksthe desiredstraight line without
falling down ( β>0
◦
).
Effect of theinitialheadingangle
In this section, we showthree simulationresults ( S 1, S 2and S 3) in which
the robottracksthe Y-axis, under different initial conditions. Thesimulation
