Yangsheng Xu, Yongsheng Ou. Control of Single Wheel Robots
Подождите немного. Документ загружается.

22
2K
inematicsa
nd
Dynamics
0 1 2 3 4 5
−1
0
1
2
3
4
5
(a)
0 1 2 3 4 5
35
40
45
50
55
60
65
70
(b)
0 1 2 3 4 5
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
(c)
−4 −2 0 2
−4
−3
−2
−1
0
(d)
˙
β [ rad/s]
β [ deg]
˙α [ rad/s]
x [ m ]
y [ m ]
t [ sec]
t [ sec]t [ sec]
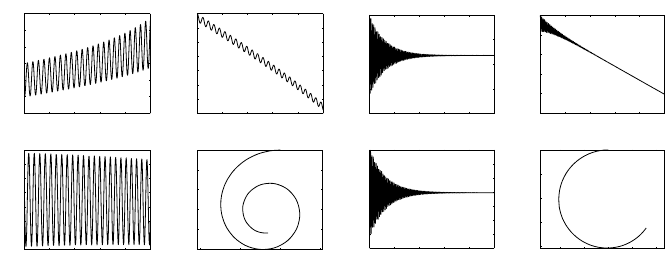
Fig.
2.2.
The
si
mu
lation
results
of
a
rolling disk without the flywheel.
0 1 2 3 4 5
−2
−1.5
−1
−0.5
0
(a)
0 1 2 3 4 5
69
69.2
69.4
69.6
69.8
70
(b)
0 1 2 3 4 5
−0.2
−0.15
−0.1
−0.05
0
0.05
0.1
0.15
(c)
−4 −2 0 2 4
−8
−6
−4
−2
0
(d)
˙
β [ rad/s]
β [ deg]
˙α [ rad/s]
x [ m ]
y [ m ]
t [ sec]
t [ sec]t [ sec]
Fig. 2.3. The simulation results of the
singlewheel robot.
flywheelonthe robot. Based on the conservation of
angular momemtum,
when
thereisachange in thetilt angle of theflywheel β
a
,the whole robotwill rotate
in the opposite direction
in order to
maintain
constanta
ngularmoment
um. It
implies that we maycontrol thelean angle of therobot forsteering. Simulation
ande
xperimentr
esults are showninFigure 2.4 andFigure 2.5,respectively,
under thesame initial conditions
β =90
o
,β
a
= α =0
o
,
˙
β =˙α =
˙
β
a
=0rad/s, ˙γ =15 rad/s,
α =0
o
.
Both Figures 2.4 and2.5 show that if thetilt angle β
a
rotatesin73 deg/s
anticlockwise at t=2.4 seconds, the lean angle β rotatesinaclockwise di-
rection.Inthe exp
eriment,the transientresponse of
β is more critical than
thesimulations. For2.7 seconds, the tilt angle remains unchanged andthen
β ands
teeringr
ate ˙
α convergetoas
teady position in
both sim
ulations and
experiments. In the experiment, we have notfound anyhigh frequency oscil-
lations perhaps because the sensor response and the sampling time aremuch
slowerthanthe highfrequencyoscillations.
2.2ModelingonanIncline
2.2.1 Motion on an Incline
Dynamicsofarolling disk
Consider adisk rolls without slippingalong an inclined plane withaninclina-
tion angle ϕ .Assume that the disk is rigid with radius R. The dynamicmodel
can be developed usingthe constrainedLagrangian method.Itissimilar to
2.2
Mo
de
ling
on
an
Inc
line
23
0 2 4 6
0
5
10
15
20
25
(a)
0 2 4 6
−150
−100
−50
0
50
100
(b)
0 2 4 6
−300
−200
−100
0
100
200
300
(c)
0 2 4 6
65
70
75
80
85
90
95
(d)
˙
β [ deg/s]
β [ deg]
˙α [ deg/s]
β
a
[ deg]
t [ sec]t [ sec]
t [ sec]t [ sec]
Fig. 2.4. The simulation results of tilt-
ingt
he
flywheel
of
the
rob
ot
with
˙
β
a
=
73 deg/s
0 2 4 6
0
5
10
15
20
25
30
a
1 2 3 4 5 6
−200
−150
−100
−50
0
50
(b)
0 2 4 6
−150
−100
−50
0
50
(c)
0 2 4 6
60
70
80
90
100
110
120
(d)
˙
β [ deg/s]
β [ deg]
˙α [ deg/s]
β
a
[ deg]
t [ sec]t [ sec]
t [ sec]t [ sec]
Fig. 2.5. The experimental results of
tiltingt
he
flywheel
of
the
rob
ot
with
˙
β
a
=
73 deg/s
the derivation in [115]&[87], except forsome components due to the gravity
act on thesystem. Twononholonomicvelocityconstraints are
˙
X = − R
˙γS
α
+˙αS
β
C
α
−
˙
βC
α
S
β
(2.35)
˙
Y = − R
˙γC
α
+˙αC
β
C
α
+
˙
βS
α
S
β
(2.36)
The rotational kinetic energy and the potential energy of the disk are given
below,
K =
1
2
m
˙
X
2
+ m
˙
Y
2
+ mR
2
˙
β
2
cos
2
β +
1
2
I
x
˙α
2
sin
2
β
+
1
2
I
x
˙
β
2
+ I
x
˙α cos β +˙γ
2
P = mg( R sin β cos ϕ + y sin ϕ )
Using the Lagrange undetermined mu
ltiplier
λ method,
theequations of
motionofarolling disk canbedetermined below
m
¨
X = λ
1
m
¨
Y + mg sin ϕ = λ
2
λ
1
Rsα + λ
2
Rcα =2I
x
¨αcβ +¨γ − ˙α ˙γsβ
λ
1
Rsαcβ + λ
2
rcαcβ = I
x
¨α (1 + c
2
α ) − 2˙α
˙
βsβcβ
+2¨γcβ − 2
˙
β ˙γsβ
C − λ
1
Rcαsβ + λ
2
Rsαsβ = mr
2
c
2
α + I
x
¨
β − mR
2
˙
β
2
cβ
+ mgRcβ + I ˙α
2
cβsβ +2I
x
˙α ˙γsβ

24
2K
inematicsa
nd
Dynamics
where c =cos and s =sin.Weeliminate the Lagrangemultipliersbyobtain-
ing
¨
X,
¨
Y .Anormal form of thedynamic equationofarolling disk is given
by
M ( q )¨q + N ( q, ˙q )=0
where M ( q ) ∈ R
3 × 3
and N ( q, ˙q ) ∈ R
3 × 1
aret
he
inertiam
atrix
an
dn
onlinear
terms respectively.
M =
I
x
+(mR
2
+ I
x
) c
2
β 0(mR
2
+2I
x
) cβ
0 mR
2
+ I
x
0
( mR
2
+2I
x
) cβ 0(mR
2
+2I
x
)
N =[N
1
,N
2
,N
3
]
T
,q=[α, β,γ ]
T
N
1
= − mgRcαcβsϕ − ( I
x
+ mR
2
) s (2β )˙α
˙
β − 2 I
x
sβ
˙
β ˙γ
N
2
= mgRcβcϕ − gmRsαsβsϕ +(mr
2
+ I
x
) cβsβ ˙α
2
+(mR
2
+ I
x
) sβ ˙α ˙γ
N
3
= − 2(mR
2
+ I
x
) sβ ˙α
˙
β
Dynamicsofasingle wheel robot
The motion of asingle wheel robot on an inclined plane differs significantly
fromthatonhorizontal
planes [21],[115]&[112]. On an incline, somecompo-
nents of thegravitational forces act on thesystem. The natureofnonholo-
nomicconstraints andthe equation of motion can be derivedasbelow. We
assume thatthe robotisah
omogeneous, rigid diskw
hichrollso
vera
suffi-
ciently roughslopewithout slipping. The high spinningflywheel is anchored
on thecentre of
masso
ft
he entire wheel.T
he dynamice
quationo
ft
he entire
system is given by
M
6
( q )¨q + N
6
( q, ˙q )=A
T
λ + Bu (2.37)
where M
6
( q ) ∈ R
6 × 6
and N
6
( q, ˙q ) ∈ R
6 × 1
aret
he inertiam
atrix andnonlinear
terms respectively.
A ( q )=
10− RS
α
C
β
− RC
α
S
β
− RS
α
0
01 RC
β
C
α
− RS
α
S
β
RC
α
0
B =
000010
000001
T
,u=[u
1
,u
2
]
T
q =[X, Y, α, β, γ,β
a
]
T
,λ=[λ
1
,λ
2
]
T
2.2
Mo
de
ling
on
an
Inc
line
25
The nonholonomic constraints of arollingdisk andasingle wheel robot on
the inclined plane areidentificalinEquations 2.35&2.36.The nonholonomic
constraints canbewrittenas,
A ( q )˙q =0 (2.38)
Aminimum set of differential equations (Normal form) is obtained when the
Lagrange multipliersare eliminated.This model(2.39) is anonholonomicand
underactuatedmodel. The model of asingle wheel robot on theground [112],
assumedthatthe climbing angle ϕ =0,isasubset of this model. The system
dynamics
can
be
de
scrib
ed
as
m
11
0 m
13
0
0 m
22
0 m
24
m
13
0 m
33
0
0 m
24
0 m
44
¨α
¨
β
¨γ
¨
β
a
+ N ( q, ˙q )=Bu (2.39)
2.2.2 Motion Planning on an Incline
Condition of rolling up
In this section, we determine the condition of rolling up of the robot on an inclined
plane. The system can be linearized around the position perpendicular to the surface
such as β = 90
◦
+ δβ, β
a
= δβ
a
,
˙
β =
˙
δβ.After linearization, the linear acceleration
of the system along the plane and the angular acceleration of the rolling diskare
¨γ =
u
1
− mgRC
α
S
ϕ
mr
2
+ I
¨
Y =
u
1
− mgRC
α
S
ϕ
mr
2
+ I
R
where I representsthe moment of thewhole robotalong the Z axis, 2 I
xw
.
Consider arollingdisk, I is set to be themoment of inertiaofthe diskalong
the Z axis. Theconditionofrollingwithout slipping holds, i.e., ¨y = R ¨γ .
Initially ˙γ,v
0
areset to be zero. The minimum value of theangularaccel-
eration of thesystem is set to be ¨γ
min
.Therefore, theconditionofrollingup
on an inclineis
u
1
≥ ( mR
2
+ I )¨γ
min
+ mgR sin ϕ
Let’s rearrangethe aboveequation so that ϕ is representasafunctionofthe
minimum angular accelerationofthe system ¨γ
min
,the moment of inertia I
andthe applied torque u
1
.
sin ϕ =
u
1
− ( mR
2
+ I )¨γ
min
mgR
(2.40)
26
2K
inematicsa
nd
Dynamics
0 10 20 30 40 50 60 70 80 90
−4
−2
0
2
4
6
8
10
12
14
x 10
−4
φ (in deg)
τ (in Nm)
τ
critical
τ
slip
Guarantee region
Slipping region
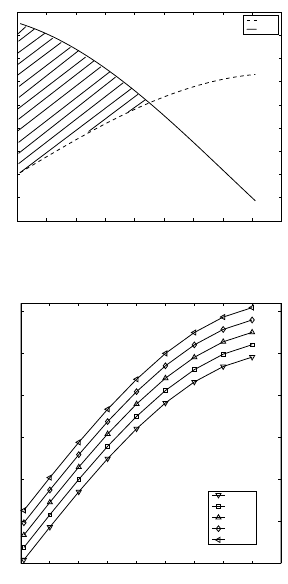
Fig. 2.6. Criticaltorque of arolling disk v.s. aclimblingangle
0 10 20 30 40 50 60 70 80 90
0
5
10
15
20
25
30
φ (climbling angle in deg)
τ (in Nm)
γ
..
min
=0
γ
..
min
=3
γ
..
min
=6
γ
..
min
=9
γ
..
min
=12
Fig. 2.7. Critical torque of therobot v.s. aclimblingangle
Figures.2.6 &2.7 sho
wt
he criticaltorques applied to
thesystem for rolling
up an inclined plane withaninclination ϕ .ReferringtoFig. 2.7,the condition
of rolling up
fora
single
wheel
robot
is
similar
to
arollingd
isk in
Fig
.2.6.T
he
curveofacritical torque looks similar to that of arollingdisk, butithas
larger magnitude.
The dynamicbalancing
We have proposed alinear state backsteppingfeedback[113]. Consider x
1
=
δβ,x
2
=˙α, x
3
=
˙
δβ,the systemscan be describedinadifferentform:
˙x
1
= x
3
(2.41)
˙x
2
= f
21
x
1
+ f
22
x
2
+ f
23
x
3
+ g
21
u
β
a
˙x
3
= f
31
x
1
+ f
32
x
2
+ g
32
We define the following control law,

2.2
Mo
de
ling
on
an
Inc
line
27
u
β
a
=
− f
21
x
1
− f
22
x
2
− f
23
x
3
+˙α
2
− k
3
( x
2
−
η
f
32
)
g
21
˙α
2
=
− (1
+
f
31
)˙x
1
− k
1
˙x
3
− k
2
( x
3
+ k
1
x
1
)
f
32
which can ensure the system to be stabilized around the position perpendic-
ular to the surface.
Planning rolling Up
In this section, we discuss how to remedy the failure of the condition of rolling
up by planning the robot motion in different angles.
Method I : Changing of the orientation. Suppose we change the direction
of heading
siny ϕ
sin φ = sin sin
= ϕ α
22
x + y
From the previous result, the condition of rolling up is
2
C ≥ ( mR + I )¨ + mgR sin
min
α sinγϕ
Now we consider the robot rolls on an inclined plane φ instead of ϕ .
1
¨Iα = 0 then ˙α = ω , α = ω t + α
zz0
2
If we set = ˙ωα= 0,
z
¨
¨mX + mR cos α = 0γ
¨
¨mY mR sin− α = 0γ
2
C mgR sin α sin I mR− ϕ = ( +)¨γ
The necessary conditions for rolling up are where C ≥ mgR sin . If theα sin ϕ
acceleration of rolling of the robot is positive then the acceleration along the
ϕ
φ
α
ysinϕ
X
Y
Fig. 2.8. Change orientation
28
2K
inematicsa
nd
Dynamics
y
vo
v
s
l
var
g0d
gd
v0
Fig.
2.9.
Disk
rolls
on
ap
lane
X and Y directions will become positive. In this way,weare sure that, in the
directionofforward motion α
0
,the robotcan roll up on an inclined plane φ .
MethodII:Change theinitialvelocities. Consider that adisk rolls along
astraightline andthen it hitsaninclinedsurface.Weassume that the robot
does notbounce at themoment of hitting andthe robotcan remain perpen-
diculartothe surface.Weincrease itsangularvelocityand linearvelocityof
the disk’s center.
I ¨γ = C − FR = C − maR,f
or
F
= ma
¨γ =
C
mR
2
+ I
,for a = R ¨γ
The angular velocityand thevelocityofthe diskare
2 Cs
IR+ mR
3
and
2 CRs
I + mR
2
respectively.Afteritcollides with thesurface,basedonthe dynamicequations
derived,
the initial
condition mu
st be
modified because ˙
γ
0
,v
0
aren
ow
non-zero
in this case. Before the hittingonthe inclined surface,wehave
¨y =
RC − mR
2
g sin ϕ
mR
2
+ I
, ¨γ =
C − mRg sin ϕ
mR
2
+ I
afterward, we
have
,
˙y =
RC − mR
2
g sin ϕ
mR
2
+ I
t + v
0
cos ϕ
¨γ =
C − mRg sin ϕ
mR
2
+ I
t +˙γ
0
When ˙y =˙y
min
,

2.2
Mo
de
ling
on
an
Inc
line
29
t =
(˙y
min
− v
0
cos ϕ )(mR
w
+ I )
RC − mR
2
g sin ϕ
y = v
0
cos ϕt +
1
2
RC − mR
2
g sin ϕ
mR
2
+ I
t
2
l =
( mR
2
+ I )(
˙
y
2
min
− v
0
cos ϕ )
2(RC − mR
2
g sin ϕ )
( v
0
cos ϕ )
2
=˙y
2
min
−
2 l ( RC − mR
2
g sin ϕ )
mR
2
+ I
If
˙
y
min
=0
,t
he
n
v
2
0
=
2 l ( mR
2
g sin ϕ − RC)
cos ϕ
2
( mR
2
+ I )
l =
v
2
0
cos ϕ
2
( mR
2
+ I )
2(mR
2
g sin ϕ − RC)
2.2.3 Simulation Study
Based on [112],wefound thatthe propertyofGyroverissimilar to arolling
diskwhen itsfl
ywheel does not spin. If
I
xf
is zero, thed
ynamics of
therobot
is exactly thesame as that of arollingdisk. The purposeofthe highspinning
flywheelistoprovide alarger resistance to the rate of
change of
leaning,
stabilizingthe robottobalance.Now,weinvestigate howthe highspinning
flywheelprovides abalancing effectfor therobot when it climbs up on an
inclined plane. In short, the robot, when its flywheel does not spin, cannot
roll up an inclined plane i.e. arollingdisk cannot climbupaninclinedplane.
It is because the
force components
mgRc
βc
ϕ
and − gmTs
αs
βs
ϕ
ared
ominant
on theroll dynamic. In the simulation,weassume that the single wheel robot
is arollingdisk with I
xw
= I
yw
=
1
2
mR
2
and I
zw
= mR
2
.Weuse the following
geometric/mass parameters from the real system throughout ours
imulations
in Ta
ble 2.3.
Robot wheel: m =15 kg,R=17 cm, I
xw
=0. 0289
Flywheel: I
xf
=0. 0063
StaticFriction : µ
s
=1Nm/ ( rad/s)
Sliding Friction : µ
g
=0. 1 Nm/ ( rad/s)
An Inclination angle: ϕ =10
◦
Table 2.3.
System parameters
Theinitialconditioninthe simulationstudyis
˙α =
˙
β =0rad/s
, ˙γ = − 15 rad/s
α = γ =0
◦
,β =80
◦
,X= Y =0
30
2K
inematicsa
nd
Dynamics
C ase I: Rolling up case
• Fig.2.10 shows the simulation of arollingdisk. It is noted that the lean
angle
˙
β of therollingdisk decreases rapidlyand thelean angle β becomes
zero.
This
meanst
he
diskf
allso
ve
r,
or
,i
ts
iner
tial
ma
trix
will
be
come
singular, whichviolates the assumption of rolling without slipping. Besides,
the steering rate ˙α rises up anddown, andthe trajectory of therollingdisk
does not go up alongthe Y axis. Therollingdisk fails to go up.
• Forasingle wheel robot,weinvestigated thesystem when ˙γ
a
=1600 rpm =
0.
It
is
clear
th
at
th
es
pinning
flywheelp
ro
vi
des
al
arge
angular
mom
en-
tum. We stabilize the robot to theuprightposition β =90
◦
,δβ
ref
=0
◦
,
suchthatthe resulting roll-up trajectory is astraight line. The feedback
gainsare k 1=− 30, k 2=− 3and k 3=3respectively.The simulation
resultsare shown in Figure 2.11. It shows that the lean angle β of the
robo
te
xp
onen
tially
con
ve
rget
o9
0
◦
andt
he
steering
ra
te
˙
α exp
on
en
tia
lly
converges to zero. The rolling speed of ˙γ becomes -35rad/s andthe trajec-
tory of the center of
therobot
oscillates at
theb
eginning andt
hen finally
is restricted to followastraightline path.
C ase II:Rollingdowncase
• Fig.2.12 shows that arollingdisk falls down very rapidlyfromstationary.
It is because 5
◦
turns in
the
lean angle fromt
he ve
rticaldirection makes
the disk fall down.
• Fig.2.13 shows
the
single wheel robot
when rolling do
wn.W
eselect the
feedback gainswhichare k 1=30, k 2=− 3and k 3=− 3respectively.It
is similar to the rolling up case. This impliesthatthe single wheel robot
is balanced along the
ve
rticalp
osition by
the tilting
of
theflywheel.
0 0.2 0.4 0.6 0.8
0
5
10
15
20
25
30
35
t (s)
α (deg)
0 0.2 0.4 0.6 0.8
0
20
40
60
80
t (s)
β (deg)
0 0.2 0.4 0.6 0.8
0
0.5
1
1.5
2
t (s)
α
.
(rad/s)
0 0.2 0.4 0.6 0.8
−10
−8
−6
−4
−2
0
t (s)
β
.
(rad/s)
Fig. 2.10. Rolling up
of
adisk

2.2
Mo
de
ling
on
an
Inc
line
31
0 0.02 0.04 0.06 0.08 0.1 0.12
0
0.2
0.4
0.6
0.8
1
1.2
Fig. 2.10. Continued
0 1 2
0
0.5
1
1.5
2
2.5
3
t
α (in deg)
0 1 2
78
80
82
84
86
88
90
92
t
β
0 1 2
−8
−6
−4
−2
0
2
t
β
a
0 1 2
−10
−5
0
5
10
t
α
.
0 1 2
−0.5
0
0.5
1
1.5
2
2.5
3
t
β
.
0 1 2
−40
−35
−30
−25
−20
−15
t
γ
.
−0.15 −0.1 −0.05 0 0.05
0
2
4
6
8
10
12
x
y
path of C.M. of robot on slope
0 0.5 1 1.5 2
−250
−200
−150
−100
−50
0
t
τ
angle= 10
o
Fig. 2.11. Rolling up of asingle wheel robot
0 0.2 0.4 0.6 0.8
0
2
4
6
8
10
0 0.2 0.4 0.6 0.8
80
100
120
140
160
180
Fig. 2.12. Rolling do
wn
of
adisk
