Yangsheng Xu, Yongsheng Ou. Control of Single Wheel Robots
Подождите немного. Документ загружается.


12
1I
nt
ro
duction
Fig. 1.6. The third prototypeofthe robot
els up to 10mph, recoversfromfalls, andruns about25minutes percharge
of
itsN
iCad
batteries.
It
ca
nc
arry
av
ideo
camera
that
lo
oks
thr
ought
he
transparentwheel, andtransmit video data to aremote receiver/monitor.
2
Kinematics andDynamics
2.1 Modeling in a Horizontal Plane
2.1.1 Kinematic Constraints
Previously, Gyrover was controlled only manually, using two joysticks to
control the drive and tilt motors through a radio link. A complete dynamic
model is necessary to develop automatic control of the system. In the following
sections, we will develop the nonholonomic kinematics constraints, as well as
a dynamic model using the constrained generalized Lagrangian formulation.
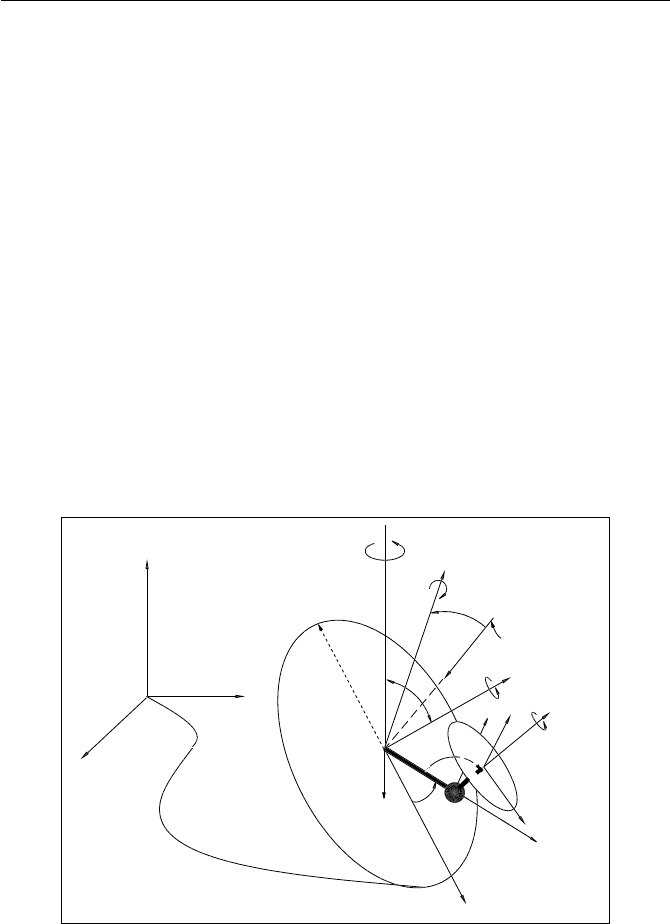
X
Y
Z
O
A
C
W
I
R
D
E
mg
l
1
l
2
θ
˙
β
˙α
α
β
β
a
˙γ
˙γ
a
y
B
x
B
z
B
x
a
y
a
z
a
x
c
y
c
Xd
irection
Fig. 2.1. Definitionofcoordinate frames and system variables
Y. Xu and Y. Ou: Control of Single Wheel Robots, STAR 20, pp. 13–32, 2005.
© Springer-Verlag Berlin Heidelberg 2005
14
2K
inematicsa
nd
Dynamics
Coordinate frame
In
deriving
the
equatio
ns
of
motiono
ft
he
ro
bo
t,
we
as
sume
that
the
wheel
is arigid, homogeneous disk whichrollsoveraperfectlyflat surface without
slipping. We modelthe actuation mechanism, suspended fromthe wheel bear-
ing, as atwo-link manipulator, with aspinning diskattachedatthe endofthe
second
link
(Figu
re
2.1).T
he
first
link
of
len
gth
l
1
representsthe verticaloffset
of the actuation mechanism fromthe axisofthe Gyroverwheel. Thesecond
link
of
len
gth
l
2
representsthe horizontal offset of thespinning flywheeland
is relatively smaller compared to the verticaloffset.
α, α
a
Precession angles of the wheel and for the flywheel,
respectively,measured about the vertical axis
β Lean angles of the wheel
β
a
Tiltangle between the link l
1
and z
a
-axis of the fly-
wheel
γ,γ
a
Spin angles of the wheel and the flywheel, respectively
θ Angle between link l
1
and x
B
-axis of the wheel
m
w
,m
i
,m
f
Mass of the wheel, mass of the internal mechanism and
mass of the flywheel respective
ly
m Total mass of the robot
R, r Radius of the wheel and the flywheel respectively
I
xxw
,I
yyw
,I
zzw
Momentofinertia of
the wheel about x, yand za
xes
I
xxf
,I
yyf
,I
zzf
Momentofinertia of
the flywheel about x, yand z
axes
µ
s
,µ
g
Friction coefficient in yaw and pitchdirections, respec-
tively
u
1
,u
2
Drivetorque of the drivemotor and tilttorque of the
tilt motor, respe
ctively
Table 2.1. Variables definitions
Next, we
assign four coordinates frames as
follows: (1)the inertial frame
O
,whose x − y plane is anchored to theflat surface,(2) thebodycoor-
dinate frame
B
{ x
B
,y
B
,z
B
} ,whose originislocatedatthe center of the
single wheel, andwhose
z -axis represents
the
axis of rotationofthe wheel,
(3) thecoordinate frame of internalmechanism
C
{ x
c
,y
c
,z
c
} ,whose cen-
ter is located at point
D ,and whose
z -axis is alwaysparallel to
z
B
,and (4)
the flywheel coordinates frame
E
{ x
a
,y
a
,z
a
} ,whose center is located at
thecenter of theGyroverflywheel, andwhose
z -axis represents the axis of
rotationofthe flywheel. Note that
y
a
is alwaysparallel to y
c
.The definition
andconfiguration of system andvariablesare shown in Table 2.1and Figure
2.1. Rolling without slipping is atypical example of anonholonomicsystem,
since in most cases, some of theconstrainedequations for the system are non-
integrable. Gyroverisasimilar type of nonholonomicsystem. Herewefirst
2.1
Mo
de
ling
in
aH
orizon
tal
Plane
15
derive the constraints of the single wheel, andthen derive the dynamic model
of Gyroverbasedontheseconstraints.Wedefine(i, j, k )and ( l, m, n )tobe
the unit vectors of thecoordinate system XY ZO(
O
)and x
B
y
B
z
B
A (
B
),
respe
ctiv
ely
.L
et
S
x
:= sin( x )and C
x
:= cos ( x ). The transformationbetween
these two coordinate frames is given by
i
j
k
= R
O
B
l
m
n
(2.1)
where R
O
B
is the rotationmatrix from
O
to
B
.
R
O
B
=
− S
α
C
β
− C
α
− S
α
S
β
C
α
C
β
− S
α
C
α
S
β
− S
β
0 C
β
(2.2)
Let v
A
and ω
B
denote the velocityofthe center of massofthe single wheel
andits angular velocitywith respect to the inertia frame
O
.Then, we have
ω
B
= − ˙αS
β
l +
˙
βm +(˙γ +˙αC
β
) n (2.3)
The constraints require that the disk rolls without slipping on the horizontal
plane, i.e. the velocityofthe contact pointonthe diskiszero at anyinstant
v
c
=0, (2.4)
where v
c
is the velocityofcontactpoint of thesingle wheel. Now, we can
express v
A
as
v
A
= ω
B
× r
AC
+ v
c
(2.5)
where r
AC
= − Rl representing the vector from the frame Ct
oAi
nFigure 5.
Substituting Eqs. (2.3)and (2.4)inEq. (2.5)gives
v
A
=
˙
Xi +
˙
Yj+
˙
Zk, (2.6)
where
˙
X = R (˙γC
α
+˙αC
α
C
β
−
˙
βS
α
S
β
)(2.7)
˙
Y = R (˙γS
α
+˙αC
β
S
α
+
˙
βC
α
S
β
)(2.8)
˙
Z = R
˙
βC
β
(2.9)
Eqs.(2.7) and(2.8) arenonintegrable andhence arenonholonomicwhileEq.
(2.9)isintegrable, i.e,
Z = RS
β
. (2.10)
Therefore, therobot can be represented by seven (e.g.
X, Y, α, β,γ, β
a
,θ),
instead of eight, independentvariables.

16 2 Kinematics and Dynamics
2.1.2 Equations of Motion
In this section, we study the equation of motion by calculating the La-
grangian L = T − P of the system, where T and P are the kinetic energy and
potential energy of the system respectively. We divide the system into three
parts: 1) single wheel, 2) internal mechanism, and 3) spinning flywheel.
Single wheel
The kinetic energy of the single wheel is given by,
T
w
=
1
2
m
w
˙
X
2
+
˙
Y
2
+
˙
Z
2
+
1
2
I
xxw
ω
2
x
+ I
yyw
ω
2
y
+ I
zzw
ω
2
z
(2.11)
Substituting Eqs.(2.3) and(2.9) in Eq.(2.11) yields
T
w
=
1
2
m
w
˙
X
2
+
˙
Y
2
+(R
˙
βC
β
)
2
+
1
2
I
xxw
(˙αS
β
)
2
+ I
yyw
˙
β
2
+ I
zzw
(˙αC
β
+˙γ )
2
(2.12)
Thep
otential energy of the single wheel
is
P
w
= m
w
gRS
β
(2.13)
Internal mechanismand spinning flywheel
We
needtocompute thetranslational androtational parts of
kinetic
energy forthe internalmechanism andflywheel respectively.Weassume that
l
2
is very small compared with l
1
,
l
2
0(2.14)
Thus, the flywheel’s center of mass(E )coincides with thatofthe internal
mechanism ( D ).
Let { x
f
,y
f
,z
f
} be the center of massofthe internalmechanism andthe
flywheel w.r.t.
O
.The transformation fromthe center of massofsingle
wheel to the flywheel can be described by:
x
f
y
f
z
f
=
X
Y
Z
+ R
O
B
l
1
C
θ
l
1
S
θ
0
(2.15)
Let T
t
f
denote the translational kinetic energyofthe flywheeland theinternal
mechanism.
T
t
f
=
1
2
( m
i
+ m
f
)[ ˙x
2
f
+˙y
2
f
+˙z
2
f
](2.16)

2.1
Mo
de
ling
in
aH
orizon
tal
Plane
17
Differentiating Eq. (2.15) andsubstituting it in Eq. (2.16), we obtain T
t
f
.We
observed thatthe internalmechanism swings slowly,soitshould notcon-
tribute highly to therotational kinetic energy.Let ω
f
be the angular velocity
of
flywheelw
.r.t.
O
.Wethenhave
ω
f
= R
E
B
ω
B
+
0
˙
β
a
˙γ
a
(2.17)
where R
E
B
is the transformationfrom
B
to
E
.
R
E
B
=
C
θ
S
β
a
− S
θ
S
β
a
C
β
a
S
θ
C
θ
0
C
θ
C
β
a
− C
βa
S
θ
S
β
a
(2.18)
Therotational kinetic energy of theflywheel is nowgiven by,
T
r
f
=
1
2
( ω
fx
)
2
I
xxf
+(ω
fy
)
2
I
yyf
+(ω
fz
)
2
I
zzf
(2.19)
Theflywheel is assumed to be auniform diskand theprinciplemomentsof
inertia are
I
xxf
= I
yyf
=
1
4
m
f
r
2
,I
zzf
=
1
2
m
f
r
2
.The potentialenergyofthe
flywheel and internal mechanism is
P
f
=(m
i
+ m
f
)(RS
β
− l
1
C
θ
S
β
)(2.20)
Lagrangianofthe system
The Lagrangian of the system thus is
L =
T
w
+(T
t
f
+ T
r
f
)
− ( P
w
+ P
f
)(2.21)
Substituting Eqs.(2.11),(2.16),(2.19),(2.13) and(2.20) in Eq. (2.21), we
mayd
etermine
L .T
here areo
nly two
control
torques av
ailable on
thesystem.
Oneisdrivetorque(u
1
)and the other is the tilt torque ( u
2
). Consequently,
using theconstrainedL
agrangian method
,t
he dynamice
quation of
theentire
system is given by
M ( q )¨q + N ( q, ˙q )=A
T
λ + Bu (2.22)
where M ( q ) ∈ R
7 × 7
and N ( q, ˙q ) ∈ R
7 × 1
arethe inertiamatrix andnonlinear
terms respectively.
A ( q )=
10− RC
α
C
β
RS
α
S
β
− RC
α
00
01− RC
β
S
α
− RC
α
S
β
− RS
α
00
(2.23)
q =
X
Y
α
β
γ
β
a
θ
,λ=
λ
1
λ
2
,B =
00
00
00
00
k
1
0
01
k
2
0
,u=
u
1
u
2

18
2K
inematicsa
nd
Dynamics
Thenonholonomicconstraints canbewrittenas,
A (˙q )˙q =0. (2.24)
It
is
notedt
hat
al
le
lementso
ft
he
lastt
wo
co
lumns
of
the
matrix
A ar
e
zer
o
,b
ecause
the
nonholonomic
co
nstrain
ts
only
restrict
the
mo
tion
of
t
he
single
wheel,n
ot
thefl
ywheel.
The
last
two
colu
mnsr
epresen
t
th
em
otion
variablesofthe flywheel. Moreover, matrix B only has three rows with non-
zeroelements since the input torques only drive the tilt angle of theflywheel
( β
a
)and the rotating angleofthe single wheel(γ ), so that the fifthand
the sixth rows of B arenon-zeroasthey represent the tilting motion of the
flywheeland therotatingmotion of thesingle wheel respectively.Furthermore,
when thesingle wheel rotates, the pendulum motion of internalmechanism
is introduced, thus θ changes.Therefore, the drivetorqueofthe single wheel
will also affect the pendulum motion of theinternal mechanism ( θ ), so that
theseventh rowofmatrix B is not zero.
Normalform of the system
In this section, we will eliminate the Lagrange multiplierssothatamin-
imum set of
differential equations is
obtained by
thesimilar way
in [18]. We
first partition thematrix
A ( q )int
o
A
1
and A
2
where A =[A
1
: A
2
]
A
1
=
10
01
,A
2
=
− RC
α
C
β
RS
α
S
β
− RC
α
00
− RC
β
S
α
− RC
α
S
β
− RS
α
00
Let
C ( q )=
− A
− 1
1
A
2
I
3 × 3
(2.25)
Then consider thefollowing relationship
˙q = C ( q )˙q
2
(2.26)
where q
1
=[X, Y ]
T
and q
2
=[α, β,γ,β
a
,θ]
T
.Differentiating Eq. (2.26) yields
¨q = C ( q )¨q
2
+
˙
C ( q )˙q
2
(2.27)
Substituting Eq. (2.27) into Eq. (2.37) andpremultiplying both sides by C
T
( q )
gives
C
T
( q ) M ( q ) C ( q )¨q
2
= C
T
( q )
Bu − N ( q, C ( q )˙q
2
) − M ( q )
˙
C ( q )˙q
2
(2.28)
where C
T
( q ) M ( q ) C ( q )is5× 5asymmetrical positivedefinite matrix function.
Note that Eq.(2.28) depends only on ( α, β, γ,β
a
,θ) .Bynumerical integration,
we can obtain q
2
from¨q
2
in Eq. (2.28), andthen obtain(X, Y )bysubstituting
q
2
and˙q
2
in Eq. (2.26).

2.1
Mo
de
ling
in
aH
orizon
tal
Plane
19
2.1.3Dynamic Properties
Understanding
the
ch
aracteristics
of
ther
ob
ot
dynamics
is
of
significance
in
thec
on
trol
of
thes
ystem.
To
th
is
end
,w
efi
rst
simplify
th
em
od
el.
Practically
,
we mayassume I
xxw
= I
yyw
=
1
2
m
w
R
2
, I
zzw
= m
w
R
2
,and l
1
and l
2
are
zero, thus the mass center of theflywheel is coincidentwith the center of the
robot. Forsteady motion of therobot, thependulummotion of theinternal
mechanism is sufficiently small to be ignored,thus θ is set to be zero. The
spinning rate of theflywheel γ
a
is set to be constant. Let S
β,β
a
:= sin( β +
β
a
) ,C
β,
β
a
:= cos ( β + β
a
) , and S
2 ββ
a
:= sin[2( β + β
a
)]. Based on the previous
derivation, the normal form of thedynamics modelis
M ( q )¨q = F ( q, ˙q )+Bu (2.29)
˙
X = R (˙γC
α
+˙αC
α
C
β
−
˙
βS
α
S
β
)(2.30)
˙
Y = R (˙γS
α
+˙αC
β
S
α
+
˙
βC
α
S
β
)(
2.31)
where q =[α, β, γ,β
a
]
T
,
M =
M
11
0 M
13
0
0 I
xxf
+ I
xxw
+ mR
2
0 I
xxf
M
13
02I
xxw
+ mR
2
0
0 I
xxf
0 I
xxf
,
F =[F
1
,F
2
,F
3
,F
4
]
T
,
B =
0010
0001
T
,u=
u 1
u 2
M
11
= I
xxf
+ I
xxw
+ I
xxw
C
2
β
+ mR
2
C
2
β
+ I
xxf
C
2
β,β
a
M
13
=2I
xxw
C
β
+ mR
2
C
β
F
1
=(I
xxw
+ mR
2
) S
2 β
˙α
˙
β + I
xxf
S
2 ββ
a
˙α
˙
β + I
xxf
S
2 ββ
a
˙α
˙
β
a
+2I
xxw
S
β
˙
β ˙γ +2I
xxf
S
β,β
a
˙
β ˙γ
a
+2I
xf
S
β,β
a
˙
β
a
˙γ
a
− µ
s
˙α
F
2
= − gmRC
β
− ( I
xxw
+ mR
2
) C
β
S
β
˙α
2
− I
xxf
C
β,β
a
S
β,β
a
˙α
2
− (2I
xxw
+ mR
2
) S
β
˙α ˙γ − 2 I
xxf
S
β,β
a
˙α ˙γ
a
F
3
=2( I
xxw
+ mR
2
) S
β
˙α
˙
β
F
4
= − I
xxf
C
β,β
a
S
β,β
a
˙α
2
− 2 I
xxf
S
β,β
a
˙α ˙γ
a
where (X, Y, Z) is the coordinates of the center of mass of the single wheel
with respect to the inertial frame as shown in Figure 2.1. M ( q ) ∈ R
4 × 4
and
N ( q, ˙
q ) ∈ R
4 × 1
arethe inertial matrix andnonlinearterm respectively.Eqs.
20
2K
inematicsa
nd
Dynamics
constraints of therobot.
We furthersimplifythe model by decouplingthe tilting variable β
a
from
Eq. (2.29). Practically, β
a
is directly controlled by thetilt motor(position
con
trol),
as
sumingt
hatt
he
tilt
actuatorh
as
an
ad
equate
torqu
e
to
tr
ac
kt
he
desired β
a
( t )t
ra
jectory
exactl
y.
Th
erefore,
β
a
can
be
de
coupled
from
Eq.
(2.29). It is similar to the case of decoupling thesteeringvariable fromthe
bicycle dynamics shown in [16],[35].
As we consider
˙
β
a
as anew input u
β
a
,the dynamics model Eq. (2.29)
be
comes
˙
β
a
= u
β
a
˜
M (˜q )
¨
˜q =
˜
F (˜q,
˙
˜q )+
˜
B ˜u. (2.32)
with ˜q =[α, β, γ ]
T
,
˜
M =
M
11
0 M
13
0 I
xxf
+ I
xxw
+ mR
2
0
M
13
02I
xxw
+ mR
2
˜
F =
˜
F
1
,
˜
F
2
,
˜
F
3
T
˜
B =
001
˜
B
12
00
T
, ˜u =
u
1
u
β
a
˜
F
1
=(I
xxw
+ mR
2
) S
2 β
˙α
˙
β + I
xxf
S
2 ββ
a
˙α
˙
β
− 2 I
xxw
S
β
˙
β ˙γ +2I
xxf
S
β,β
a
˙
β ˙γ
a
− µ
s
˙α,
˜
F
2
= F
2
,
˜
F
3
= F
3
,
˜
B
12
= I
xxf
S
2 ββ
a
˙α +2I
xxf
S
β,β
a
˙γ
a
,
Eq. (2.32) showsthe reduced dynamicmodel of the single wheel robot af-
ter decouplingthe tilting varible β
a
,with newmatrices
˜
M (˜q ) ∈ R
3 × 3
and
˜
F (˜q,
˙
˜q ) ∈ R
3 × 1
.The realistic geometric/massparameters areshown in Table
2.2. It is notedthatifthe lean angle β is set to be 0
o
or 180
o
,meaning that
the single wheel robot falls on the ground, itsinertialmatrix
˜
M will become
singular because it violates the assumption of rolling without slipping.
The robotdynamic modelishighly coupled, nonholonomic andunderac-
tuacted. Because themajor part of therobot is arollingwheel, therefore it
processes thetypical characteristics of arollingdisk. Forarolling disk, it
does notfall when it is rolling, because thereisagyroscopic torque, resulting
from the coupling motion between the roll andyaw motions, forbalancing the
gravitational torque. However, itsrollingrate must be high enough to pro-
vide asufficient gyroscopic torquefor balancing thedisk. When we installed
(2.29) and(2.30),(2.31) form the dynamics modeland nonholonomicvelocity

2.1
Mo
de
ling
in
aH
orizon
tal
Plane
21
Singlew
heel
parameters:
m =1. 25kg
,R
=1
7
cm
Internal mechanism : m
i
=4. 4 kg,
Flywheel
parameters
:
m
f
=2. 4 kg
,r
=5cm
Friction coefficients: µ
s
=1Nm/ ( rad/s) ,µ
g
=0. 01Nm/ ( rad/s)
Table 2.2. Parameters used in simulation and experiments
aflywheel on the wheel, the robot’s gyroscopic torqueisgreaterand depends
less on its rolling speed ˙γ ,owing to the high spinningflywheel, the lean angle
of the robottendstoremain unchanged.Wecan explain this characteristics
basedonthe equilibrium solutionofEq. (2.32). Forthe lowyaw rate and
¨α =
¨
β =¨γ =0,
˙
β =0,u
1
= u
β
a
=0
,E
q.
(2.32)
be
comes
0=gmRC
β
+(2 I
xxw
+ mR
2
) S
β
˙α ˙γ +2I
xxf
S
β,β
a
˙α ˙γ
a
, (2.33)
From Eq. (2.33), theterms ˙γ ˙α and˙γ
a
˙α areused to cancel the gravitational
torques gmRC
β
,inorder to stabilizethe roll componentofthe system.Be-
causethe spinning rate ˙γ
a
is very high, theterm 2 I
xxf
S
β,β
a
˙α ˙γ
a
is significantly
large, in order to
cancel the gravitational torque, ev
en
though
the
rolling sp
eed
˙γ is low. Thus, it will achieveanequilibriumsteeringrate ˙α
s
,
˙α
s
=
− gmRC
β
s
2 I
xxf
S
β
s
,β
a
˙γ
a
+(2 I
xxw
+ mR
2
) S
β
s
˙γ
(2.34)
foraspecific lean angle β
s
.
Figures 2.2and 2.3abo
ve
sho
wt
he simu
lationresults of
arollingd
isk
without the flywheel, andthatofthe single wheelrobot, respectively,under
the same
initial
conditions
β =70
o
,β
a
=0
o
,
˙
β =˙α =
˙
β
a
=0rad/s, ˙γ =15 rad/s,
α =0
o
.
Note that the lean
angle
β of ar
ollingd
isk without
the flywheel decreases
much rapidlythanthatofthe single wheel robotasshown in Figures 2.2(b)
and2.3(b). This verifiesthe stabilizingeffect of the flywheel on the single
wheel robot.InFigures 2.3(a),(c), under the influence of friction in the yaw
direction, the steering rate ˙α andthe leaningrate
˙
β will convergetoasteady
state solution as shown in Eq. (2.34). Otherwise,anunwantedhigh frequency
oscillation will occur.Practically, it will not produce asignificanteffect on the
system because the frequency of theabove oscillationismuchgreaterthan
the system response. If the rolling rate is reduced, the rolling disk will fall
much more quickly than in the previous case.
2.1.4 Simulation Study
Up to now, we only consider the case when theflywheel’s orientation is fixed
with respect to the single wheel. Here, we will focus on thetilting effect of the
