Yangsheng Xu, Yongsheng Ou. Control of Single Wheel Robots
Подождите немного. Документ загружается.


4.3
Le
arningC
on
trol
with
Limited
Tr
aining
Data
103
In this problem, we mainly face three typesoferror. The first type of
error is measurementerror, which is derivedfromthe sensorreading process.
We call it observationerror. It mayexist in both X and Y .The second type
of
erroro
ccursd
ue
to
the
diff
erence
be
twe
en
the
tru
e
map
ping
functiona
nd
some
fixedn
eural
net
wo
rk
st
ructure.
We
call
it
str
ucture
error.
As
pro
ve
nb
y
Cyb
enk
o[
28]
in
1989,
mostf
unctions
(in
cluding
an
yc
on
tinu
ousf
unctionw
ith
bounded support) can be approximatedbyfunctions of aone-hidden-layer BP
neuralnetwork. Thus, we omit this type of errorinour following discussion
andassume that we alreadyhaveagood enough structurethatallows us to
approximate anyfunction, if we choose suitable parameters forthatstructure,
i.e. thereexists θ
∗
,suchthat
Y = F ( X )=f ( X, θ
∗
) , (4.74)
where θ
∗
=(θ
∗
1
,θ
∗
2
,..., θ
∗
h
)
T
, h is the number of thestructureparameters. The
last type of erroristhe parametererrorand it is the result of theestimating of
the best suitable parameters. The three typesoferrorare closely related to the
estimation error. To
compensate for the
observatione
rror, more training data
lead to better results. At thesame time,the parametererroralso requires more
trainingdata to ov
ercome the
overfitting problem, whichw
ill be
discussedi
n
more detail in next section. Thus, the
estimationerrorc
an be
reduced, but
notremovedabsolutely, because it is impossible to collect infinite training
samples.
Next,wewill address ourproblembyconsidering these errors, individually.
Let Y
o
be the observations fortrue Y .Let
Y
o
= Y + ,
where hast
he Gaussiandistribution with
E ( )=0an
dv
ar
ia
nc
e
σ
2
> 0. If
X
o
be the observation of X ,
X
o
= X + ε,
where ε ∈ R
m
.Here, we assume each system state x
i
hasthe similarobser-
vation error as Y .The distribution of ε hasthe form N (0,σ
2
I
m
). Here, we
have adata table,whichincludes theobservation forbothinputs andoutputs
to train aneural network as alearningcontroller.The data table comes from
discrete time sampling fromhumanexpert controldemonstrations. In fact,
from the data table, we have Y
o
and X
o
,but not Y and X ,thuswemodify
Equation (4.74) to
Y
o
= f ( X, θ
∗
)+. (4.75)
Usually,observation errors are much smaller then their truevalue. ATaylor
expansion to the first order can be usedtoapproximate f ( X
o
,θ)interms of
f ( X, θ )
f ( X
o
,θ) ≈ f ( X, θ )+(L
X
f )
T
· ε, (4.76)
where L
X
f =(
∂f( X,θ )
∂x
1
,
∂f( X,θ )
∂x
2
,...,
∂f( X,θ )
∂x
m
)
T
.

104 4 Learning-based Control
We focus our attention on the estimation of regression function f , here,
for θ
∗
. We show that for a fairly broad class of sampling scheme t
i
with a
fixed and identical sampling rate ∆ > 0. Assume that (
ˆ
f )isanestimationof
Y fromar
andoms
ample
T of
size
n .T
he
system
is
represent
ed
by
Equation
(4.75). Theleast-squares estimate of θ
∗
is
ˆ
θ ,w
hic
hi
so
btainedb
ym
inimizing
the error function given in (4.77)(forneural networks,the errorexappropri-
ation algorithm is acommon method forminimizingthe errorfunction). The
predicted outputfromthe modelis
ˆ
Y
o
,asshown in (4.78)
S ( θ )=
n
i =1
[ Y
o
i
− f ( X
o
i
,θ)]
2
(4.77)
ˆ
Y
o
i
= f ( X
o
i
,
ˆ
θ )
= f ( X
i
,
ˆ
θ )+(L
X
f )
T
· ε.
(4.78)
If themodel provides an accurate prediction of the actual system behavior,
then
ˆ
θ is close to the truevalue of theset of parameters θ
∗
andaTaylor
expansion to
thefirst-order canb
eu
sed to
approximate
f ( X
i
,
ˆ
θ )inter
ms
of
f ( X
i
,θ
∗
)
f ( X
i
,
ˆ
θ ) ≈ f ( X
i
,θ
∗
)+(L
θ
f )
T
· (
ˆ
θ − θ
∗
) ,
where L
θ
f =(
∂f( X,θ
∗
)
∂θ
∗
1
,
∂f( X,θ
∗
)
∂θ
∗
2
,...,
∂f( X,θ
∗
)
∂θ
∗
h
)
T
.T
hen, Equation (4.78) turns
to be
ˆ
Y
o
i
≈ f ( X
i
,θ
∗
)+(L
θ
f )
T
· (
ˆ
θ − θ
∗
)+(L
X
f )
T
· ε. (4.79)
Thesubscript value of o is given to denote the set of observation points
other than that used forthe least-squares estimation of
θ
∗
.Byignoringthe
second-order small
quantityand using Equations(4.75) and(
4.79),Equation
(4.80) gives the difference between the newobservation Y
o
0
andthe predicted
valu
e
ˆ
Y
o
0
,and Equation (4.81) gives theexpected value of thedifference.
Y
o
0
−
ˆ
Y
o
0
≈
0
− ( L
θ
f
0
)
T
(
ˆ
θ − θ
∗
) − ( L
X
f
0
)
T
· ε
0
. (4.80)
E [ Y
o
0
−
ˆ
Y
o
0
] ≈ E [
0
] − ( L
θ
f
0
)
T
E [(
ˆ
θ − θ
∗
)] − ( L
X
f
0
)
T
E [ ε
0
] ≈ 0 . (4.81)
Because of
thestatisticali
ndependencea
mong
0
,
ˆ
θ and ε
0
,the variance can
be expressed as
var [ Y
o
0
−
ˆ
Y
o
0
] ≈ var [
0
]+var [(L
θ
f
0
)
T
(
ˆ
θ − θ
∗
)] + var [(L
X
f
0
)
T
ε
0
] . (4.82)
Thedistribution of (
ˆ
θ − θ
∗
)can be approximatedashaving the distribu-
tion N (0,σ
2
θ
[ F
.
(
ˆ
θ )
T
F
.
(
ˆ
θ )]
− 1
)in[24]. TheJacobian matrix F
.
(
ˆ
θ )has theform
shown in Equation(4.83),where the single periodisplaced to accord with the
notationsused in [93] whichdenotes that the matrix has first-order differential
terms

4.3
Le
arningC
on
trol
with
Limited
Tr
aining
Data
105
F
.
( θ
∗
)=
(
∂f( X
1
,θ
∗
)
∂θ
∗
1
)(
∂f( X
1
,θ
∗
)
∂θ
∗
2
) ··· (
∂f( X
1
,θ
∗
)
∂θ
∗
h
)
(
∂f( X
2
,θ
∗
)
∂θ
∗
1
) ··· ··· (
∂f( X
2
,θ
∗
)
∂θ
∗
h
)
.
.
.
.
.
.
.
.
.
.
.
.
(
∂f( X
n
,θ
∗
)
∂θ
∗
1
)(
∂f( X
n
,θ
∗
)
∂θ
∗
2
) ··· (
∂f( X
n
,θ
∗
)
∂θ
∗
h
)
(4.83)
va
r
[ Y
o
0
−
ˆ
Y
o
0
] ≈ σ
2
+ σ
2
θ
( L
θ
f
0
)
T
( F
T
.
F
.
)
− 1
( L
θ
f
0
)+σ
2
( L
X
f
0
)
T
( L
X
f
0
)]. (4.84)
Thematrix F hasthe dimensions n by h ,where n is the number of samples
and h is the number of parameters θ ,whichcomposes
ˆ
θ .Tofind the effects of
moresampling data on var [ Y
o
0
−
ˆ
Y
o
0
], we needthe following useful result.
Lemma 1 Let A and D be nonsingularsquared matrices of orders k .
Then,provided that theinverses exist,
( A + D )
− 1
= A
− 1
− A
− 1
( D
− 1
+ A
− 1
)
− 1
A
− 1
. (4.85)
Proof: Averificationispossible by showingthatthe product of ( A + D )
− 1
andt
he right-hand sideo
fEquation (4.85)isthe identit
ym
atrix.
If we have more trainingsamples´n = n + n
1
,let
´
F
.
( θ
∗
)=
(
∂f( X
1
,θ
∗
)
∂θ
∗
1
)(
∂f( X
1
,θ
∗
)
∂θ
∗
2
) ··· (
∂f( X
1
,θ
∗
)
∂θ
∗
h
)
(
∂f( X
2
,θ
∗
)
∂θ
∗
1
) ··· ··· (
∂f( X
2
,θ
∗
)
∂θ
∗
h
)
.
.
.
.
.
.
.
.
.
.
.
.
(
∂f( X
´ n
,θ
∗
)
∂θ
∗
1
)(
∂f( X
´ n
,θ
∗
)
∂θ
∗
2
) ··· (
∂f( X
´ n
,θ
∗
)
∂θ
∗
h
) .
(4.86)
Thematrix
´
F hasthe dimensions ´n by h .Then,
´
F
T
´
F = F
T
F + F
T
1
F
1
, (4.87)
where F
1
is similarly defineda
si
nEquation (4.83), but
n is substituted with
n
1
.Let X be a h × 1v
ector. Since
F
T
F and F
T
1
F
1
arep
ositive
definite matrices,
substituting A = F
T
F ,and D = F
T
1
F
1
,inEquation(4.85),wehave A
− 1
and
A
− 1
( D
− 1
+ A
− 1
)
− 1
A
− 1
arepositive definite, provided that they exist. From
Lemma 1 ,
X
T
( A + D )
− 1
X ≤ X
T
A
− 1
X. (4.88)
Then,fromEquation (4.87)
X
T
(
´
F
T
´
F )
− 1
X ≤ X
T
( F
T
F )
− 1
X. (4.89)
Hence, when h is fixed,the larger is n ,the smaller is var [ Y
o
0
−
ˆ
Y
o
0
]. However,
forour problem, that n is not large enough,thus, the majorerrors come
fromthe second term of Equation (4.84). In this chapter, we propose to use
unlabelled trainingsamplestoreduce the variance of Y ,i.e., to decrease the
learningerror. The methods will be addressedinfollowing sections in greater
detail.Ifwedefinethe data in thedata table (whichhas been collected from
106 4 Learning-based Control
human demonstrations) as labelled data, we then call the new data unlabelled
data, which are produced by interpolation from the labelled data. Let (
´
X,
´
Y )
be oneunlabelled data point.
If
we
assumedt
hatt
he
in
terp
olation
pro
cess
is
a
nu
nb
iased
estima
tion,
then
let
´
X = X +´ε,
´
Y = Y +´, (4.90)
wherethe distributionsof´ε and´ have the form N (0, ´σ
2
I
m
)a
nd
N (0, ´σ
2
).
Sincethe unlabelled data areproducedfromoriginalobservation data ( X
o
,Y
o
),
they
will
ha
ve
larger
errors
than
the
or
iginald
ata,
i.e.,´
σ
2
>σ
2
.Both thesen-
sor readingerrorand the independentinterpolation error arecorrelative with
each other.Assume that totally ´n ( >n)unlabelled data points areproduced.
If the unlabelled data areused to train the neural network, we needtoupdate
Equations(4.75) -(4.84) with Equation (4.90). Finally, we have
var [ Y
o
0
−
ˆ
Y
o
0
] ≈ ´σ
2
+ σ
2
θ
( L
θ
f
0
)
T
(
´
F
T
.
´
F
.
)
− 1
( L
θ
f
0
)+´σ
2
( L
X
f
0
)
T
( L
X
f
0
)], (4.91)
where
´
F
.
is defined in
Equation(
4.86) and´
n is the numb
er
of
unlabelled sam-
ples used to obtain θ .Since ´n>n,wereduce the second term of var [ Y
o
0
−
ˆ
Y
o
0
].
However, the first termand third termare notrelativetothe samplenumber
n ,but the accuracy of the trainingsample.Infact,byusing the unlabelled
trainingdata we
increased them.
The final result of
var [ Y
o
0
−
ˆ
Y
o
0
]i
sd
ependent
on thecompetition of thethree terms.Inmost cases,especially,when theorig-
inal trainingdata is ve
ry sparse,t
he second term in Equation (4.91) dominates
the learning error. Thus, by using unlabelled data, we can reduce the learn-
ing error. However, whenthe number of unlabelled data continue to increase,
thee
ffect of the other two
terms will be
larger than the second
term, finally.
Moreover, theinterpolation error mayalso be larger, i.e., ´σ will increase. This
is because of the overfitting phenomenon. Thus, using toomuchunlabelled
data will not necessarily lead to better learning results. Later simulationswill
also demonstrate this point.
The Overfitting Phenomenon
Here, we choose neuralnetworks to realize thefunctionregression. Many of
the importantissues concerning the application of neuralnetworks can be
introduced in the simpler context of polynomialcurvefitting. The problem is
to fit apolynomial to aset of N data points by atechnique of minimizing
errorfunction. Consider the M th-order polynomialgiven by
f ( x )=w
0
+ w
1
x + ... + w
M
x
M
=
M
j =0
w
j
x
j
. (4.92)
This can be regarded as anon-linear mapping which takes
x as input andpro-
duces f ( x )asoutput.The preciseformofthe function
f ( x )isdetermined by

4.3
Le
arningC
on
trol
with
Limited
Tr
aining
Data
107
thevalues of theparameters w
0
,..., w
M
,whichare analogous to theweights in
aneural network. It is convenienttodenote the set of parameters ( w
0
,..., w
M
)
by the vector W .The polynomial can then be writtenasafunctionalmapping
in
the
fo
rm
f = f ( x,
W
).
We shall labelthe data withthe index i =1,..., n ,sothateachdata point
consists
of
av
alueo
f
x ,d
enoted
by
x
i
,and acorresponding desiredvaluefor
the
ou
tput
f ,w
hic
hw
es
hall
deno
te
by
y
i
.
Arti Scholkopf [15] pointed out that the actual risk R ( W )ofthe learning
machine is expressed as:
R ( W )=
1
2
f (x,W) − y dP (x,y) . (4.93)
Theproblemisthat R ( W )isunknown, since P (x,y)isunknown.
The straightforwardapproachtominimize the empirical risk,
R
emp
( W )=
1
n
l
i =1
1
2
f (x,W)
i
− y
i
,
turns outnot to guaranteeasmall actual risk R ( w ), if the number n of
trainingexamples is limited. In
other wo
rds: as
mall error on
thetraining set
does notnecessarily imply ahigh generalization ability(i.e., small error on
an independenttest set). This phenomenon is often referred to as overfitting.
Fo
rt
he learning problem, the
St
ru
cture
Risk Minimization
(SRM)p
rinciple
is based on thefact that forany W ∈ Λ and n>h,with aprobabilityofat
least 1-η ,t
he bo
und
R ( W ) ≤ R
emp
( W )+Φ (
h
n
,
log ( η )
n
)(
4.94)
holds,where the confidence termΦis defined as
Φ (
h
n
,
log ( η )
n
)=
h ( log
2 n
h
+1) − log ( η/4)
n
.
The parameter h is called the VC ( Vapnik- Chervonenkis)dimension of a
set of functions, whichdescribes the capacityofaset of functions. Usually,to
decrease the R
emp
( w )tosome bound, most ANNs with complex mathematical
structures have avery high value of h .Itisnotedthatwhen n/h is small (for
example less than 20,the trainingsample is small in size),
Φ hasalarge value.
When this occurs, performance poorly represents
R ( W )with R
emp
( W ). As a
result,accordingtothe SRM principle, alarge trainingsample size is required
to acquire asatisfactorylearningmachine.
We can illustrate this by aone-dimensionpolynomialcurvefitting problem.
Assume we generate trainingdata fromthe function
h ( x )=0. 5+0. 4sin(2πx)+, (4.95)
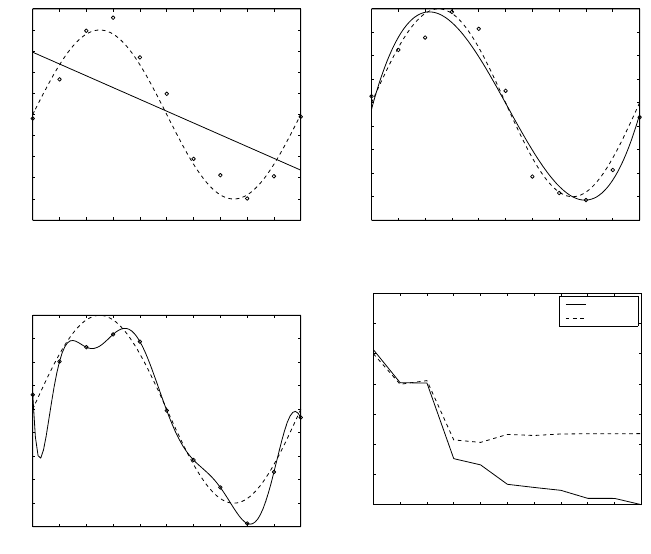
108 4 Learning-based Control
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
x
h(x)
Fig. 4.13. Linear regression M=1.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
x
h(x)
Fig. 4.14. Polynomial degree M=3.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
x
h(x)
Fig. 4.15. Polynomial degreeM=10.
0 1 2 3 4 5 6 7 8 9 10
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
order of polynomial
RMS error
training
test
Fig. 4.16. The RMS error for both train-
ing andtest sets.
by sampling the function h ( x )atanequal interval of x andthen adding ran-
domn
oisewith Gaussian distribution ha
ving
astandard deviation
σ =0. 05.
We will therefore be interested in seeinghow close thepolynomial f ( x, W )is
to the function h ( x ). Figure 4.13shows the11pointsfromthe training set,
as we
ll as the function
h ( x ), together with the result of
fitting alinear poly-
nomial, givenby(4.92) with M =1.Ascan be seen, this polynomial gives
apoorrepresentation of h ( x ). We can obtain abetterfitbyincreasing the
order of thepolynomial, since this increases the number of the freeparameter
number in the function, whichgives it greater flexibility. Figure 4.14shows
theresult of fitting acubic polynomial ( M =3), whichgives amuchbetter
approximation to h ( x ). If, however, we increase the order of thepolynomial
toofar,then theproximation to theunderlying functionactually gets worse.
Figure 4.15shows theresult of fittinga10th-order polynomial ( M =10).
This is nowable to achieveaperfect fit to the trainingdata. However, the
polynomial has fitted the data by developingsome dramaticoscillations. Such
functions aresaid to be over-fitting to thedata. As aconsequence,this func-
tion gives apoorrepresentationof h ( x ). Figure 4.16shows aplot of R
emp
for both the trainingdata setand the test data set, as afunctionoforder
4.3
Le
arningC
on
trol
with
Limited
Tr
aining
Data
109
M of thepolynomial. We see that the trainingset error decreases steadily as
theorder of thepolynomial increases.The test seterror, however, reaches a
minimum at M =3,and thereafterincreasesasthe order of thepolynomial
is
increased.
4.3.2Resampling Approach
Our purposeistoimprovethe functionestimationperformance of ANN learn-
ing controllers by using thepolynomial fittingapproachinterpolation samples.
Let
x
T
i
= { x
i
( t
1
) ,x
i
( t
2
) ,..., x
i
( t
n
) }
be an originaltraining sampleset of onesystem state, by the same sampling
rate ∆>0a
nd
T
j
=(X
j
,Y
j
),
where
X
j
= { x
1
( t
j
) ,x
2
( t
j
) ,.
..,
x
m
( t
j
) } is
an
original trainingsample point. An unlabelled sample set
¯
T = {
¯
T
1
,
¯
T
2
,...
¯
T
N
}
whic
hh
as
thes
ize
of
´
n can
be
ge
neratedb
yt
he
fo
llow
ing.
Step 1 Using the original trainingsample set x
T
1
to produce thesegment
of local polynomial estimation ˆx
1
( t )of x
1
( t )with respect to time t ∈ ( t
1
,t
n
).
Let
x
1
( t )=ˆx
1
( t )+´,
whereˆx
1
,x
1
,t∈ R
Step2Repeatstep 1toproduce thelocal polynomialestimationˆx
i
( t )
( i =2, 3 ,..., m )and
ˆ
Y ( t )of x
i
( t )(i =2, 3 ,..., m )and Y ( t )with respect to
time t ∈ ( t
1
,t
n
).
Step3Divide the sampling rate ∆>0by k =´n/n +1to produce new
sampling time
in
terv
al
∆
k
= ∆/k.Weproduce new unlabelled samples
´
T by
ac
ombination of interpolatingt
he po
lynomials ˆ
x
i
( t )(i =1, 2 ,..., m )and
ˆ
Y ( t )
in the newsampling rate.
Figure 4.17shows an example of oneunlabelled trainingsample generation
process.Inour method, unlabelled trainingsamplescan be generatedinany
number
.
Barron [8]has studiedthe way in whichthe residualsum-of-squares error
decreasesasthe number of parameters in amodel is increased. Forneural
networks he showedthatthis errorfallsas O (1/M
), where M
is the number
of hiddennodes in aone hiddenlayer network. By contrast,the erroronly
decreases as O (1/M
2 /d
), where d is the dimensionalityofthe input space for
polynomials, or indeed anyother series expansion in whichitisthe coeffi-
cientsoflinear combinations of fixed functions that areadapted. However,
fromthe formeranalysis, the number of hiddennodes
M
chosencannotbe
arbitrary large. Forapractitioner, his theory provides the guidance to choose
the number of variables d ,the number of network nodes M
,and the sample
size n ,suchthatboth 1
/M
and(M
d/n)log n aresmall. In particular, with
M
∼ ( n/( d log n ))
1 / 2
,the bound on themean squared error is aconstant
multiple of ( d log n/n)
1 / 2
.
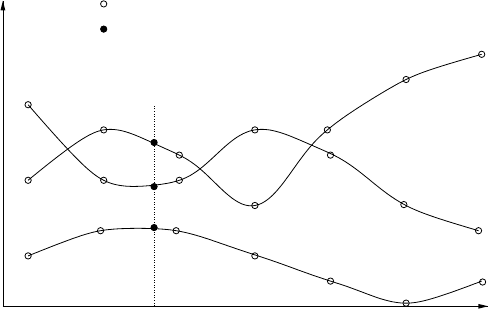
110 4 Learning-based Control
t
1
tt tttt
23
4567
t
22
Y(t)
x(t)
x(t)
1
2
Original training sample
Unlabelled training sample
Fig. 4.17. Examples of the unlabelled sample generation, when k =3.
Unlabelled trainingsample data canbeproducedinany large number by
interpolation. Prov
ided this condition, if
we
choose some
suitable andlarge
number of nodes ( M
), we can obtain averyhigh learningprecision. At this
time, thelearningerrori
sm
ainly derivedfromthe polynomialc
urvefitting,
instead of neuralnetwork learning.However, we have improvedthe learning
by
these original limited trainingsamples, fort
he learning problemh
as turned
the inputs from x ∈ R
d
to t ∈ R
1
.Byusing this approach,wehaveturned
am
ultivariate function estimationtoau
nivariate function estimation(i.e.
one-by-one mapping).
From Equation (4.91), the estimationaccuracy of this interpolation process
is important, foritwill affect the firstand third terms in Equation (4.91)
andfinally, thelearningcontroller.Inthe nextsection, the localpolynomial
fitting algorithm foro
ne dimensionalp
olynomial curvefitting is introduced
as afurtherimprovement.
4.3.3Local Polynomial Fitting(LPF)
Advan
tages
of Local Po
lynomial Fitting
Compared with the traditional methodofpolynomialcurvefitting, thereare
threemain advantages in using the LPF method.
First, polynomial curve fitting is aparametric regression method,basedon
an important assumption that the estimation modeliscorrect. Otherwise, a
large bias will inhibitprecision. LPF as anonparametricregression approach
removes this assumption.Thus, the approachcan be feasible forany model
in unknown form and still retain auniform convergence.

4.3
Le
arningC
on
trol
with
Limited
Tr
aining
Data
111
Second, LPF is awell-defined approachfor functionestimation, whichis
basedonrigorous theoretical research. To obtain an ideal estimationperfor-
mance,moreworkonpolynomial curve fitting is required,suchasthe order
of
po
lynomials
ch
osen.
Third,
LPF
requiresn
ob
ou
ndary
mo
difications.
Boundary
mo
difications
in polynomial curve fitting are averydifficult task.
In
tro
duction
to
Lo
cal
Po
lynomial
Fitting
Let X and Y be two random variableswhose relationship can be modelled as
Y = m ( X )+σ ( X ) E =0,var( )=1, (4.96)
where X and areindependent. Of interest is to estimate theregression func-
tion m ( x )=E ( Y | X = x ), based on ( X
1
,Y
1
) ,.
..,
( X
n
,Y
n
),
ar
andoms
ample
from(X, Y ). If x is not arandomvariable but y is, their relationshipcan be
modelled as
Y = m ( X )+E( )=0,var( )=1.
If the ( p +1)th derivativeof m ( x )atthe point x
0
exists, we
can
approxi-
mate m ( x )locallybyapolynomialoforder p :
m ( x ) ≈ m ( x
0
)+m
( x
0
)(x − x
0
)+... + m
( p )
( x
0
)(x − x
0
)
p
/p! , (4.97)
for x in an
eighbo
rhood
of
x
0
,byusing Taylor’s expansion. From astatistical
modellingv
iewpoint,
Equation(
4.79) models
m ( x )l
oc
allyb
ya
simple
poly-
nomial model. This suggests using alocallyweighted polynomialregression
J
h
( x )=
n
i =1
{ Y
i
−
p
j =0
β
j
( X
i
− x
0
)
j
}
2
K (
X
i
− x
0
h
) , (4.98)
where K ( · )d
enotes an
on-negativew
eight(
ke
rnel)f
unctionand
h -ban
dw
id
th
-determines the size of the neighborhood of x
0
.If
ˆ
β =(
ˆ
β
0
,...,
ˆ
β
p
)d
enotes the
solution to the aboveweighted least squares problem, thenbyEquation (4.97),
ˆ
β estimates m ( x ).
It is more convenient
to write the
abov
el
east squares problem in
matrix
notation. Denote by W the diagonal matrix with entries W
i
= K ((X
i
− x
0
) /h).
Let X be the design matrix whose ( l, j )th elementis(X
l
− x
0
)
j − 1
andput
y =(Y
1
,...Y
n
)
T
.Then, the weighted least squares problem (4.98)can be
written in matr
ix form as
min
β
( y − Xβ)
T
W ( y − Xβ) ,
where β =(β
0
,...β
p
)
T
.Ordinary least squares theory provides the solution
ˆ
β =(X
T
WX)
− 1
Wy,
112 4 Learning-based Control
whose conditional mean and variance are
E (
ˆ
β | X
1
,...X
n
)=(X
T
WX)
− 1
Wm
= β +(X
T
WX)
− 1
Wr,
var (
ˆ
β | X
1
,...X
n
)=(X
T
WX)
− 1
( X
T
ΣX)(X
T
WX)
− 1
,
(4.99)
where m = m ( X
1
) ,...m( X
n
)
T
, r = m − Xβ,the residualofthe localpolyno-
mialapproximation,and Σ = diag [ K
2
{ ( X
i
− x
0
) /h} σ
2
( X
i
)].
At first glance,the aboveregression approach lookssimilar to the tradi-
tional pa
rametric
approach
in
wh
ic
ht
he
funct
ioni
su
sually
globa
ll
y
mo
delled
by apolynomial. In order to have asatisfactorymodelling bias, thedegree M
of thepolynomial oftenhas to be large. But this large degree M introduces
an over-parametrization, resultinginalarge variabilityofthe estimatedpa-
rameters. As aconsequence theestimated regression functionisnumerically
unstable.I
nm
arke
dc
on
tr
ast
to
this
parametrica
pproac
h,
the
tec
hnique
i
s
local ,and hencerequires asmall degree of thelocal polynomial, typicallyof
order p =1
or occasionally
p =3.
4.3.4 Simulationsand Experiments
To illustrate the behavior of using the unlabelled trainingdata method for
solving the
small sample
size
problem, whic
hisproposed in the foregoing
section, we presenthere anumerical study,whichshows theresult that the
theory in this ch
apterw
orks.All of
thesimulation tasks arec
ompletedin
MATLAB.
Forthe simulationstudy, we want to buildatwo-input and one-output
model. Their relations are as
follows.
x
1
( t )=0. 5+0. 4sin(2πt)+
1
x
2
( t )=− 0 . 6+0. 3cos
(2πt
)+
2
Y ( t )=cos(x
1
)+sin( x
2
)+x
1
x
2
+
3
,
(4.100)
where, the distributions of
1
,
2
and
3
have thesame form N (0,σ
2
)and
σ =0. 01. Thesampling ratesare identical as ∆ =0. 1 s both for trainingdata
andtesting data. Fortraining data,the time interval is t
0
=0and t
T
=1s ,
suchthattotal n
o
=11data points in table 4.3 andfor testingdata, thetime
interval is t
0
=0. 05 and t
T
=0. 95s ,s
ucht
hatt
otal
n
1
=1
0d
ata points
in
table 4.4. Sincethe maximfrequency Ω
h
of thesystem in Equation(4.100) is
1 Hz andthe samplingfrequency Ω
s
is 10Hz > 2 Ω
h
,itsatisfies the“Shannon”
Theorem.
We use atwo-layerradial basis network structure. Thefirst layerhas radial-
basisneurons. The second layerhas pure-line neurons, andwecalculate its
weighted input with dot-prod.Both layers have biases. We usedMATLAB
function “ newrbe ”with “spread=0.1”, to train theneural network. Then, we
use theEquation (4.101) as evaluating function with the testing data for
