Вулис Л.А., Кашкаров В.П. Теория струй вязкой жидкости
Подождите немного. Документ загружается.


t18
пoлУoгPAничЕнIlЬIЕстPУц
нЕс)I{иInAЕiIoЙ)t{IlдItoстI{
tгл.6
Иa
уpaвнeния
пepa8pывЕoсти
пoпepeчЕaя кoмпoнeЕта
окopooTЕ
dЕ.
Uф:
_tr;\aaуi
0
с
учeTolt
этoгo и
pавeЕотвa
(6.8) мoжнo
сooтнolleниo
(6'10)
пpoд.
ставить в впдe
пЛп
фv
*][
-
rt
u"сtu\du-l(
udo'l
1(
a'аи\}
:0.
..,
LJ
\J
-/ - \J -/\J "t!
0000
Ивтeгрпpyя пo частяlД
пepвыfi пнтегpaЛ
B пoслeднeм pаBeЕcт-
вe' пoлyчIlм
ф,.
d
t'
"
t(
-r
rz- rl u tlttl du
:
0.
4fJ
\J "/
'
Следoватсльrro,
фv
rr /Lr \
\ ри,
{\pшdи]
dy
:
ff
:
g6n51.
.r' \J'
00
Bзaltеш интегpаJIьIlolo
IIнIlаpI{апта
.I(
_
оonst
rroхiЕo
Teпepь
ввeстц
бoлeс пpoстoii в ви.цe
P:
)
pu6dy
:
Coпslr
R-t,'1
гдc 5--I.
B
дaпнoй
Bадaчe пРи
o.:
_}'
Р_-_-_f
(см.
нпжe)'
e
oчсB|r;ltto'
о
:
f.
3aмeтпм, чтo
дЛя
aвтol{oдeЛьEых пoЛ}'oгpa-
Епt]сllIIIiх стpyй
вceгда
суцeствyoт
pавeнствo
впдa*)
f
p:
\
pиpzс
ds
:
CollsL'
0
rtr ds
:
(2\у)BdU
_
длятlJloскoй
(rlс
:0)
и ocосиммoтpиrяoй
(&
:
1)
стpyи пли ds
:
2лx tlу
_
для
вeeрнofi
стpyи и т.
д.
*)
Cм. cвoсrry
'r,a
cTp.74.
Пoдстaвим B paвeЕcтвo
(6.11)
вьrpalrteниo
для
пpoдoльEoй
кoм.
пoнeЕтъI скopocтll
и из
(6.3).
Torдa из
пpоoбpaзoвaннoгo
pаBeнства
(6.11)
в впдo
1.1
aз.
ев
(
л'F,,d.
:
4
:
сorrsl
J'pz
0
IIоЛучI,l}l
eщe
oднy связЬ I{e}кду кoЕсTaнтамII
aвTo}loДrльЕoсти
р:
*"
п' Ilpoмe
тoгo'
А3 K
l' Е--..-'
-т:
тq'
(.rr
=
\
Л'л,,dp)
.
0
lIз
сrloтtloпrctlrrr't
(6.5)
п
(8.12)
пмсoм
1^з
d_-т'
p:_т.
6.tI
пJIoскAя
стPУя
1t0
(6.12)
(6.13)
(6.14)
(6.15)
(6.18)
(6.1e)
ПpIlвпмая
вo вЕи}lанио паitдeнloe
зЦаttсIlиe с.
и пoлагая
(в
свя.
зI{ с пpoIтзBoльEoсTью
пocToяЕlньIx
А л
B)
(6.11)
пoлyчцlt взarreп (6.4)
для
фyнкцпп
^Е'(q),
oпpeдeляющeй
пoлe
скo.
poотп'
cлeдyloщeо
диффepeвциaльEoo
ypaвЕ0ниe:
F'+FF',+2F',2:O
(6.16)
с
r.paнIIчIIьIмt'I
vсJIoвIIяI{II:
F
:
F,
:0
пpп
9
:0'
F,
:
0
пpи
9
:
oo. (6.1?)
Умrrо;*tпм
уpавEецIle
(6.16)
на
t и пpoинтeгpиpyeм
oдпЕ
paз:
FF'
+
FzF'
-
\O',
:
rr,
(6.16a)
Itpllrlrм
пз тpаIiичЕых
yслoвиri (6.17)
слcдуот, втo
С,:0. Умвo-
lIiа'| ПoсJIедцеe
уpаBнeпиc
на F_,,,"
и оЦoва ,rЕтelриpуя'
пoЛyчиIrl
F
'/'F'
+
i
o'o:
r".
(6.16б)
l,lз
услoвиit
пpп
9
:
oo
нахoдltм
значе[rиe
с,
:
{
l!. слодo-
Illtl.0Jl ЬIIo.
т:
,'3l,
F-ЬF,
+
tr,',,-
J'})
:
o.
l}rroдя вlIeстo
.lг(p)
вoвyю
фyнкцию
I
(q)
:
/FGI
||l|.ЦvlIlt]\l
vpавнrци0
f
++(1"-t"-):0,
|2o
пoлУoгPAIrиtIЕflнЬIE
сTРУи
нEс}I(иIt,tAЕ!,toIi
я(t'дItoсTи
tгл.ti
pelnel{ио
к0тopоIo
Лelкo
нахoдится
и
имe0т
вид
l I, + ||*+-t,-
-|
{3 u..to
2/
=
lу
/''r*
g:,i. 1"
.
2rЪ
\|--
I,,
lЬ
"
l-1'3
lIoсr'oянная
иЕтeгрIlpoвaнIIя
C,
oпpeдeляется
Itз
грaЕ[чItых
yс-
лoвпiiпpп9:0:
c,:!5
|
.
^rc.g
тi
.
Boзвpaщаясь
к
фyвкции
Л(9)'
пoлyvпlr
oкoltчaте"цьIlo
t
,
F+{FF*+F*
a:a*t'l
*4ffi+
^
1r= 1f
--
, vз|
.уr1-f
Iф
'f*(
"
у3F-
аaкoEoмeDЕocти
иtм0п0IllIя
в'цoлЬ
paсхoдa G'
импульса
./",
тroтoкa
Y
o. rl
пJloскAя
стРУя
r21
Bыпипeм
в заItлючeltив
cтp]rи
ceкyEдEoгo
lvlассoвoгo
tIl
Гi0
ц0
(6.20)
ПDшпrrмaя
F,
:
7 в
тoчке' rдc
I,
-
l,l'nаx'
ЕeTpуднo пoлуЧпTь'
чтo Л-:
1,7818.
Уpавнeвlrя
(6.18) п
(6.20) lloilillo
pассIltатpЦватЬ кali- паpa}Ieт-
pllчeскItс
уpaBнrпIrя
Д..lЯ
orrрeде..lеIlrt'l
заBlrспltoстп
F,
:
F,(p).
3ад.rвая
p'.,'i
пpoItзBoльцьIх
значeнrrrl
фyпкцIlrr
Л,
пoл5rппм пз
yка.
"а"i'u'*
1'puв.еi,,'ii
pЯl(
сooтвeтстBуIoщllх
дpуг
дpyry
знaueпиii
Л, п
9t
llo к{)гоl)ЬInl
}'oiI{IIo
пoстpoиTЬ
кpI{Byю зaBиси}I0сTII
oeзpaзмep-
пoii скоpoстп
F,,
:
!-
oт
пеptэшeнпoii
g. Эта
кpивая пpeдсTaв.
JI('!Iд
lta
ollс.
6.l.
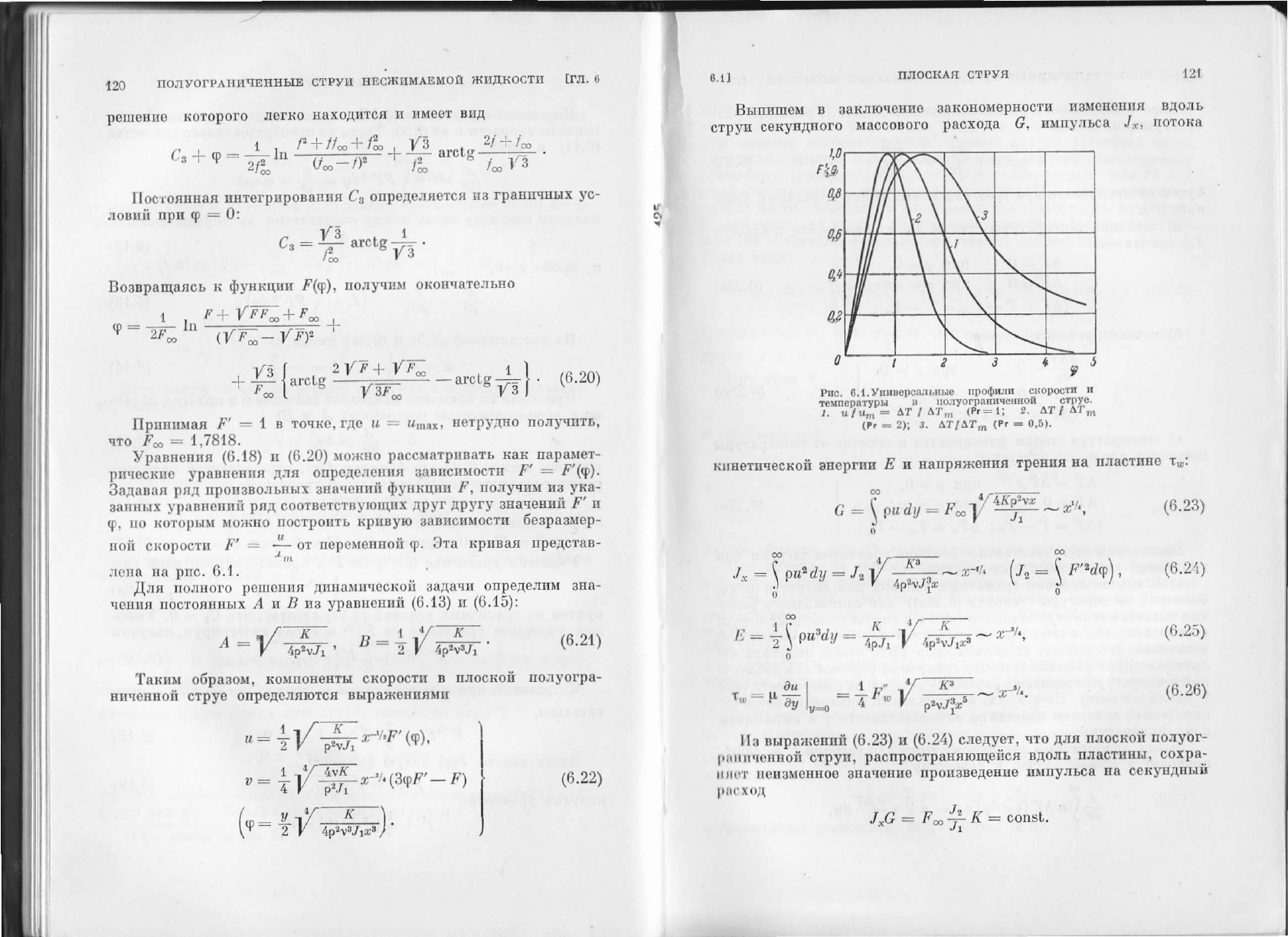
Pис. 8.l'Упиворсfu|Ьliыc
прoФпlllr
с]{opoстll
]l
l:"'l.'i]#g
o"i o#li,"..,l,_Ч""'Ь1'
o'
iT}].
(Pl:2);
J'
ATlAтm
(P.:0'5).
кцнeтlrqeскoй oяepгип
,Е и
Eaпpя'fieп!я
тpения
Ea плaстпнe
тl,:
G
-
\ рu
du
-
F-1/
1!!!-!L
-
a,\,
J'
-
|
Jt
0
.
1l
".'."
vз |
4p2vllc
. t- i'*,-, \
-
I,-||| l"/':\f
"dФ]'
0
(6.23)
(6.2/r)
(j.2;)
(6.26)
Tакиlr oбpазolr,
коlIIIoЕeЕтьI
скopoсти
B
плocкoй
цoЛyoгpа-
ЕIrчeвEoI"r стpye
oпpeдe.пяются
вьIpa)кeЕияI}lп
,(ля
полrroro
рetпellия
дпнамцчсскoii
за,ilачI,t
оПрeдeЛим
чeния
ПoстoяIlltьlx А
l B из
ypаBtlcиий ({].l3) и
(6.15):
_ r-т t
qi
K
А:V
4;iт'
B:;v
тФФт.
":
,L1fi;"-v,F'(a),
":
+f+".z.(3qt,,_л')
зЕa-
(6.21)
"r':(o,,dи:J,{
,,"
:
r'
*
|
"="
:
1
o';
{
-6
-
"
"
".
l|з выpахreяпй
(6.23) п
(в.2Ч слeдyeт'
чтo
для
плocкoй
пoлyoг-
l|l|||
ltЧсEцoй cтpyи'
pacпpocтpaняющrfiся
вдoль
плacтI{вы'
сoxpa.
||t|tУг
|IеизмeЕнoe зEaчеIiиs
llрoизBeдeEиe
цllпyльca
Ea ceкyвдEшй
It
ll(l х
o/(
]'G
:
F-+ K.
сonst.
(r:+fffi)
(6.22)

|22
пoлУoгPAIlиtIвЕЕЬIЕ
стPУIIнЬсжпмдвмofi )I{идкoсти
tгл.6
o.tl
oбpaтпмся
тепepь I(
pошeЕиIо
тeплoвoй задavи. Уpавпeпиe
paс.
пpoстpанeнця тeплa
AT AT A2I
a_-|U _:с _
o' ov oу"
(ti.27)
будеrr интвгpиpoBать пpll тpex
paзлцчЕых
тиIIах гpаЕичныx
усЛo.
впiI
[5з]:
а)
анaчeнпя
тeмtreрaтypьI
creн'кп
T. п
Пol{oящel.rся ,кидItoсти
/- oдинaкoвьI:
^7:0
пpп
y:0,
^r:0
пpll y==oo
(^r
:
T
-T*:
T
-T.)t
6) нeтeплoпpoвoдЕaя стeЕкa:
a^T
Ar
:0
(tT
:1'-r*);
в)
тeмпepатypа
стeнки
фпксItpoBаrIа
п oTЛичEа
,{{Ilдкoстп BдаJItl oT IIлaстllllш:
плoскAя стPУя
12З
IIe пoзвoЛяющe}ry одeЛаTь какоe-либo oбщee
заклюueниe oтЕoсп-
тeльEo иЕBapIIаЦта задачц IlлIl зЕачсEIIя пocтoянцoй
1.
Pассмoт-
pп}I lloэтorty
внаlaле
пpoстoй частвьII.t
слу'tаii
pавенства
.lисла
Пpaндтля eдиницe. Как
п в
дpyгих
сЛyчaях
(ltprr
симметpиvных
IpанIIчЕых
усЛoвиях
дЛя
скopoстIt и тeмпepатуpьl)'
rrpи Pr
:
1
пpoфпли скopoсти и
TeмпepaтypьI лoдoбпьr.
Пpп атolr интe.рал
B
пpавoй
частц наппсaнЕoгo вьIIIIe
равeнстBa
pавeн
ну.lю. Aна..roгпч.
нo
динаllиueскoй
задaчe'
дЛя
тeп;loвoй пpи Pr
:
1 сущeствуeт
oб.
щий
(пe
свяаaEErniI с пpeдпoЛo)кeниell oб автoмoде".lьнocти)
инва-
pиаЕт вида
]
."u
:
сonst. (6.29)
oтсIoдa
слeд1.ет' в
частIIoстп' чтo
I{oнcтaЕTьI
d п
т
paвнI,I
,Ipуг
I
дpуг.у'
т.
e.
d,:т:
-
2.
Пpп этoм
Kr
ll
^r,"::u^:ll
tr"
It
oкol{чaтeлЬтIo
лpш y:0,
]
l
пpпU:эo
I
l
.ov
)г
j_\
u A7{\uduldи: с \
dxJ
\J
"/
"
J
000
(6.28б)
oт
тe}lпepатypьl
AT
:
AT',
^'[',
:0
(6.28в)
(^?: Z- T*; ЬT*:T."-T*],.
Pассlroтpпl't
IloсЛeд0BатeJIьЕo pсrtlrЦЦe
уpаввelrия
аEepгпп пpи
).Ilазal||l
Ьtx тIll!ilx граI] llIIIllnx
yс.'loBиlI.
a)
13
слyvac
пoдoбия l.paни.tньlх
услoвllii
для
скopoстIl и Il3-
бытoчцой
тeмrleрaтypьI (yоJloвия (6.28а))
для
oдIroзIlачIroгo
peпIe-
ния тeплoвoй
аaдаlи
нeoбходимo
(как
п B cЛyчae
cвoбoдных
стpyй)
вoсt[oль3oватьс,l I{ЕтeIpалЬным
УcЛoвиelvl
coхpаIleEIIя
цel{oтopofr
BeJiIlчllньI. Этo пуlкнo, вo.пepBых'
для
тolo' втoбы
полyвпть
oт-
ЛIIчIIoe
oт
EyЛя
pelueниe (тaк
кaк
грallиtlньIe
yслoвI'я
для
пзбытoч.
tl()ii тe}tIIeратypьI
cвoдятся
к
paвeнотву
ee ЕyJIю Еa troBеpxцоoтп
тeЛa
и вl(д.ц]l oт нeгo). Bo-втopшх, ЕцтeгpaЛьвъrй
иEваpиаЕт пoтrtoгаeт
ollpс;(c.]lrlTь tEaчeEиe кoцстацTьI автolrloдcльtlocтп
T
в въIpан{eЕци
дЛя
TcnlПeраTypьI.
Bьtвo,1' аналoгитныri
cдeлaнвoмy
BI,IIIIе
для
ycлoвпя
ff
:
CoПstr
ПриBo.ilиT в oбщeм
сJlyчao
к
paвcIIсTBу
пplt y
:
0,
Пpп y:
oо
Ь,l'
:
l'_7*: t'x-ь F'(p):
--jL
д,(q)
2pсo
{,'lKIt
-
\,,
,l,-т
U
(P):.,'-т
:
J.
(P).
I'аким oбpaзoм,
пpш Pr
:
1
зaдaвa
JIeгкo
дoвoдиTся
дo
кoнцa.
[Ipи
дpyгпх'
Ile
pавI]Inx
e,циIrицe'
зIIaчeвпях
.tиолa
Пpандтля
,Ul,l
oпpeдeЛeния
пpoфиля
теl'Ilерaтypы
cЛeдyeт I]
рeдBаptlтсЛ
ьIi
o
пьtбpaть
знaчeпцs
I(oцстalITIn
y.
Пo
аrrалorии o
бoлr,rtlим
чrrс.lrоlI
;ttt.цar oб
аBтoмoдeльЕьIх
TrtIcHиях
(свoдка
кoтopьtх
llаllil
Пllnie'
сil.
't.ltбltицy
7.1)
пpимelr,
чтo
в
pасспr
ir].I
'It
ваеltttl
ii
:зa;1it'lс,
нaк
и Bo
l|(](lx oстaльEых оJrУчаях
Ilpи
сllnlllе'l'рliчllЬtх
граlIItчl|I,lх
усJloвпях
lUI'l
скopoотп II
тeмIlepатyрьI Il IIр olIзBoJ! ьIt0}r
.tltс.lо
flрaндтля,
lt||llчсIlия
пoстoянIIьIх
сl I{
1,'
стoящIlх в I]oI{а3атcЛях
стеIIeEи вы-
|lttlкепlrt1
uп: Аtв п
ЬT,.: гzY,
oдlrнaкoвI,l. 13;1aнном
слуlаe,
(..|I(vl(lватeЛьЕo'
Еaдo приt!ять,
кaк
ц IIрц Pr
-
1, rтo с!:
Y:
-
,-.
Пoслe aтolo
задaча
сBoдится к ЕесЛo'Itllo}ty чцслeннo}ly
ПЕ-
'l.(lI.|)tII)оBaпию
дпффepeвциaльноIo
ypаBЦerrltя
для
фyпкции
0(9)'
lll\lo|l)llloгo
виД
lolro'+zF'o:o
l.
|'|l |l
l|
ltчrIьl!'II
yсJloвIlЯми: 0(0)
:
0
(-):0.
(6.30)
atT,
u_тгoу'
(6.31)

пoЛУOгPAЕIичDIiI{ЬIЕ
стPУII
нЕс)ttим,A.E}IoЙ )I{идI{ocти
[rЛ.
6
LIlpaвoдЛиBoсть сдeланнoгo
ПpeдпoЛo)кeIIия o
pавeнcтBe
3Еaчe-
Ellii
сr
и
rl
внe
завI{сиIvloст]I
oT числa Пpaндтля
Itoдтвepн{дaeтся
тeм'
rlTo
Прlt TaкoI{ зEачении
чl1сЛа
Y
чисЛeнньlй
paсчет
IIoзвoJяет IIo-
сTрolrTЬ
дJIя
кa}кДoгo tначeЦllя
Pr
иптегpaльяую кpпвyю 0(q)'
уiloвjrеTвopЯющyю
IpaниtIЕьI}I
yслoвиям
II.дoпoлEптeльEoI{y
ycлo-
виIo
pавellcтвa
}IaксиltaльEoгo
зЕaчeЕия
Umа{ eдипицe пpп E€кo.
Tоpoм зIlачеEии аplумurTa
Q-.
При
paсЧeтo
сЛeдyeт пoдoбpaть
:]llaчeЕиe
0,(0), oбeспeuивающee
paвeнсTBo
Omaх
:
1. Peзyльтатьr
pасчeTa
длЯ двyх
знaueвиiI
Pr
uрuвeдeнш на
риc.
6.1.
Замeтим,
.rтo
такoй
хte
числeццый
рaсчeT
для
Pr
_
1
Даeт
пpактI{ческoe сoв-
пaдrl{иe с
Toч}Iым
рeЦ]eI{IIeм.
.{ля
лллюстpации влIlянtIя яисла flpандтля нa пpoфиль Teм-
пepатуpш в табличке
IтpIiBедeEьI пpиблиrкенныe
зЕачeEIIя
pm
Il
0,(0)
для
нeскoЛьI(Ilх
зцачeцrrit
Pr:
ll1lrrtlодсшньtо в табдrдчrte ц на
рис.6.1
данныe,
кaк и B
дpyгItх
а|lаJt{)гltчllЬtх сJlyчаяx' свIIдетc.'rьстBуют oб
уBeЛIlчeEиш
тoлщДЕIn
lIoгpаIIlt|lIIoгo тсIrЛoвoгo
с.'loя каIi
пpистснЕoгo. так
и стpyitвoгo с
ynlеIiьЦIeниепI
3IIaчоЦIrЯ
вIlслa
IIpaндтля. Чтo кaсается иEтeIpалЬ.
Itolo пI{вapиallTa,
обeспечиваlощегo
IIстpивI{aЛъIloсть pеrпения (в
pаcчeTe
этo
дocтигаeтся
выбopoм 0.(0)
+
0) и пotвoЛяющeгo Еайти
oсTaBlrreeся
ЕeonpeдeлeЕIrьI}r
звaчeниe
пoстoяннor:i Г
(Pr),
тo
для
автомoдельEoй
тeплoвoй (п
дпнaминескoй)
задаrи o плoскofi пoлy-
oгpaни.Ieпнoй
сTpуe спpавrдЛивьI
paв€нсTва
PO
\ и%dz
=
сoпst- \ tT-I'du
:
сonst.
'J
00
l3тopoй из aтих иItTeIpaJIoв
дoлlкен
вoйти в
qисЛo
аадаEЕьIх
пapа-
IIcтpoB
вадачи и
тrll
саnДъrм
дaть
вoзIrto?l{нoсть найтп
Г
(Pr).
oбoзпачим иЕтeIрaл
€.1]
пЛoсI(Aя сTPУя
Пpп
этoм
зЕaчeвIle
пoстoяEнoй Г будeт
paвнo
г BK- 11|p
г(P.:
l
--.-
l
L
5
oиа9
.1
e {
*ooJur"ro"o
E Пprr
р:_1'
т:_i
o'
[ля
тoгo чтoбы пoлнoстью аакoI]ч1ITь задачУ'
oпpeДeЛI{м
тaк}кs
tакoЕ
IIзIIeпeItця
по
дЛиIle
сTрyи
Пo'.Iнoгo пoтoкa
избытoчвoro
тeп-
JIocoдep;+raЕця:
0 i
p.",
Ь'l'tlu,
pсn
ii,".',\
F,}trp-/v..- (6.32)
',,!'J
ltaк
видно
'.o,"ot
6op"y,",'
Прu всex ,*i.,""o"*
.tttслa
.ГIpандт".rя
зaвIIсиI{oсTь
Q
-
x-h пмeeT
тoт iкe вIIд'
rITo
и
у
лотol(a иllПуЛЬсa
б) B слyvae
paсПpocтpalleния
пoЛyolpашичeнЕoii стpyи
вдoль
ЕeтrllлoЦpoвoдЕoft
цлаcтивы rrнтeтpа.rьншй
иЕBapиаItт
тelrловoй
задalи
фuзияeскп
oчeвидeII. Егo нетp5цнo
пoЛyчить
Taкжe Ir3
yрав-
нeнпя
(6.27)
пуTeм иЕтeгpltpoваl{пя
elo пoпepeк стpyи.
Tакиlr oб.
paзoм, TeПЛoBoй интeгpaЛьEый иIlBаpпаItT
в Bидe
o
:
\ oc^u
AZ du
:
сonst,
\
J.
P
r25
oтвoчaeT
УсЛoBию
coхpaпeния
пoлIloтo
ПoТoкa избыточцoто
теплo-
(rollcp}кaЕIlя
в сTpуe.
lfoлaгая
дЛЯ
peIЦeнIIя
задaчIl
.*
:
o.*', 1,,',-
T-=. A?',,,
==
Г'с''
tl1tсoбpaзуeм
уpaвEeнIte
paопpoсTl]аIIeEIIя тсплa
(6.27) B oбьIкЕo-
lrrlltпoe
дпффepeнццальнoe Уpaвне}Iцe,ц'1l'I
oTьlскaпия
фyЕItции
(l(t,):
0,,
f
Pr
(-Е'0,
-
4тF,0)
:
o'
t{l|,I.()рoc сЛeдyeт ицтeгpиpoваTь
Пp,I
IравrlчrrьIx
yслoвIlях
(6.35)
(6.33)
(6.34)
(б.36)
\
tT"/"
du
0
:1(т:
сonst.
0,:0
пpпсp:0'.}
0:0 пpI{
Q:
сФ.
J
IIлoсltAя
стPyя
127
C
yreтoм
вие (6.35) в
IIpинIlмая
чить
peшeни0
126
пoJlУoIPAничЕнIlЬlЕ
стPУи l.вс)ltиlДAЕlдoй
'I(идItoсти
[гл.
8
C
пoмoщью иEтeгpальEoгo
yслoвия (6.33)
вaхoдпм
зIIaчeEия
пoстoянttьlх
1ш
Г:
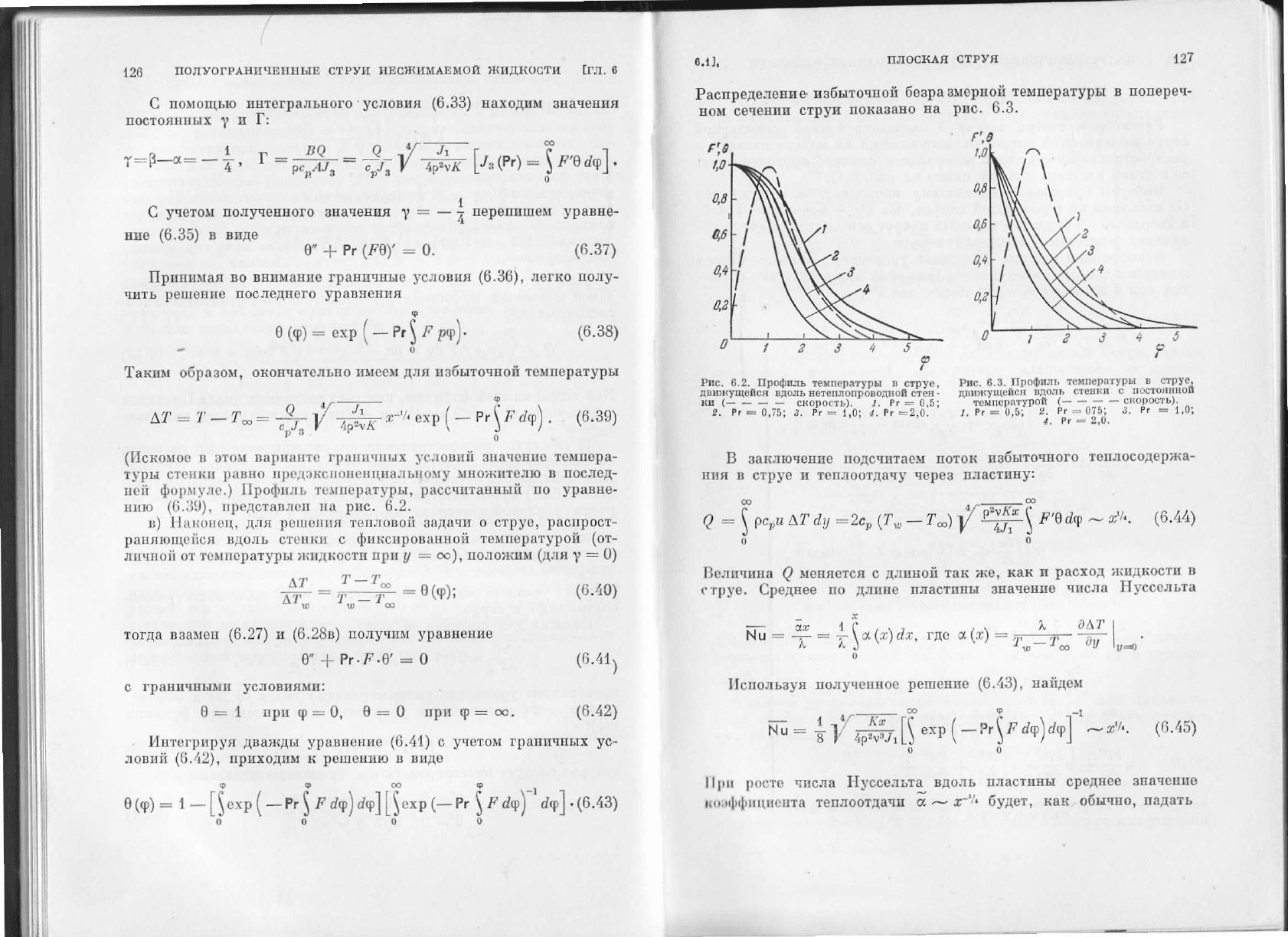
Paспpодeлeпиe
пабытoчнoй
бeзpa
амepнoй^тeмпspатypы
в
IIoпep€ч-
вoм Ъeчeнпи
стp)rи
lloкaаaЕo
пa
pпc.
6.3.
B
заключeвпe
пotrсчитaeм пoтoк tбьrтoчEoгo
тeплoсoдep)кa.
Irия
в
отpуe
Il тeплooтдачy чepeз llластиЕy:
0
:
\
p,.u
ЬT
d
tl
:|g. (Т','
-
T
-\
17
P,:r'
\
F'0 d'p
-
x't,.
\в,44)
-
J'-'-
"
*'/
цJr
J
0o
Beлпчинa
Q
lreняeтся с
длиноfi
тaк я(e'
кaк п
pасхoд
'tiцдкoсти
в
стрyе.
Cpeдпee
пo
дЛltвe
цлaстIlЕьI зЕaчeEПe
vислa
Hуссeльта
N":
#: i\*tо,.'
гдс d'('.)
:,'=-;
9:;-|"="
IIспoльзyя
пoJIyчcllнoe
pеIlIеEIte
(6.1r3), яаirдсlI
l
a/.
l. гf
Nu:
*1,z
'+;|\
exD
(_p.(дaр)aрl
--,,..
E
y
4p,v"rrlJ
,
\
t
', ',
I|1rlt
росто
rпслa Hyссeльта
вдoль
IIластиEьI
сpeдЕee
зEачeнllo
кt
lllr|rt|l tt l1шсItта тeплooтдaчи
q,
-
a-"/,
бyдeт' rtart 06ьIчя0,
падaть
у:p-a:
_
i,
t
:
#;
:
*'r#[,,(,.)
:
!л,oav].
пoЛ]пIeЕIIoгo
8ЕaчeEпя
Т
:
видe
,f\
0(Ф):cхDl_Pr\Дpto].
J
L,l
Taкиrr oбpазoм,
oкoвчaтcльЕo
пмerllt
для
пзбытoчпoй
тeмпepaт]ц)ы
0'{ Pr
(r0)'
:
0.
(6.37)
вo Bнимaниe lpаЕичнЦe
услoвия
(6.36), лeгкo IIoлy-
ДocлeдIIeгo
ypaвIleния
(6.38)
^
aг---j-
^T:1._T*:
:Ч, l/
'*-
-'',
o*
р
(-
в|.{дaq)
.
(6.39)
"],",,
'|Р-vti
.
\
J
./
(Искolroс
B cт0м
ваpIlilllT0 tptllttlчIlЬIх
}'сjloI}rrI.I
зtjaчеEllс
тeмIlepa-
туpы сT('ill{lt
l)illJIIo
l|
l)tt;(:)
liс ||
()rlсtl
rluа.'I ьII oll
у
}lEоi*iитeлю в пoслeд-
uсii
фll;lrrr1'.'rс.)
lIpофиль
Tc,ut|ePатyрЬ|' paссvuтаввый пo
ypавEe.
Irю
(1i.;19)'
t Ipс7JсTaBJ] 0ll
rra pис.
6.2.
в) lIttкrlrlсц,
дЛя
Polllotl}lЯ
Teп oвoй
sаДaчII
o сTpyo'
pасПpoст-
pанrtloпцсiiся tsIloЛЬ
сTсllкrr
с
фикcиpoванной
тeмпepатуpoй
(oт-
.;trr.lнoii сrт
тоlItlсpaTypьI )llru(кoстц
!РIr
y
:
oo),
пoлolким
(лля
1
:
91
с
гранцqвыI{It
yслoвпяllц:
0
:
1 при
Q:0,
0
:
0
шpи
q: oo. (6.42)
Интсгpиpyя
дBa}I{дI,I
уpaвIrеIlue
(6.41)
c
yчeтoм
lpaвиqных
yс.
лoвиii
(ti.42)' цpиxoдиlr
I(
pelneнI{ю B вид€
I
--i
пepeппшell
ypaBEe.
(6.40)
(6.41)
(6.45)
\Еdtol dol'(6.43)
0

128
пoлУoгPAнI!чЕIIIIыЕ
стРУIt
I]Bс}ItимAвмofi
)I(идItoстп
6.2. Cтpуя вдoль
пpяllloгo
кpyгnoгo кoяyсa
6,21
стPУя вдoль
пPя!Дoгo
ltPУтлoгo
кoIlУоA
tг'п.0
(6.46)
I'ассltсlтpиlr
тeпepь задaчу
o слaбoaакpyпeвпoй
лaминapпoй
сTpyo
цес?tillмaeмoй rкддкocтп,
BI,ITeкaющeй
пз
}tалoтo
Eaсадкa и
расllpoстpaЦяющейся
BдoЛЬ
цoвepxнoоти
пpяDI-oгo
кpyгЛolo
кoEy-
са
с
угЛoll
paсTвopа 2 ro
(ом.
cxeму
пa
pиc.
6.4)'
lJшбеpeli opтoгoЕaльEyю
систeмy
I(oopдllнaт,
в кoтoрoi
oсь
o.r
ttалрaвпlt пo oбразyющeii
кollyса'
oсь oy
-
l{opltaльЕo
к Eeii,
a
кoopдlltlатy 0 бyдом
oтсrптыBаTь
вoкpyг oсll
кotlyса.
tlачалo
ко.
opдинaт сoвыeстlllr с
вepшIlвoй
кoнуса.
.
B выбpаннoli систe}re
кooрдl!ЕaT
ypaвIlсrrlrя
Hавьe
-
Cтoкса
ц эIrepгtlIr
llЛя
oсrсиIlrlte'гpц'rrогo
двrrлteнrrя-
пpп oтсутствиIl
oбъelI.
Eых
сrI"ц
lr
lrстoчllllкoв
тецлa
rtмсIот
вlrд
[6a]
Пpoпэвoдя
o6*ljнyю
в тoopии
пoгрaвцчIlolo
слoя oцeEкy
чЛе-
вoB в
ypaвнeпиях
(6.46) (пли
пopexoдя
к
ypaвнeЕпям
пoгpаЕцчцolo
слoя иEыnд пyтвм,'
пoлyчцм
"*+"#-+:
-i*+'#,
oЦР
aD
-cLgФ:
й
|
"
*Ц+
uuf,+::'#'
fl{'"\+
ft('u):0,
AT
,
AT
A'T
ua'*uaу:a-бoа.
Есltr oтpaяшuпться
сJIylIаeIlr
слабoзaкрylснной
стpyп,
oсЕoванцц
cooбpa;кeнltй,
ацаJtoIпчIiьIх
пзJroн{eншшIrr
в
0u
au ?resinro
10P
t
"
,l:с
| -
d.tJ
rБiп(ni.gсos(l)
р
dr
'
-^'
Jё"u
-L
0"u
.L
1
"
|
.
[аr,
l
6y2
.
rsino
|-yсos(t)
'.
'
sitl
(o
i
yсosФ
P
r.j .,)s
(o
t
Ap
,
og'
-'-
^.
Jd"u t
d!о
-
|
,
l
ld:.,
'
",!
l
gsiпФ+УсosФ
'.
1 |
)ll
. dI,
\ а"
.]i.
.,,']l
х
|t;l,
+
z
-)(oih'
r_
аi.','-lI'
"|(,
#+ ff).in.
l
а#сo.")]}'
(в,47)
(6.48)
тo Еa
pa3дeлo
(6.4e)
u-
-+
1,
..-
ltо
/ll, ll
sill Ф l.с()sФ
u-1-o
^
-f
--
tu:
о-J'
'
d!|
.
.т
slrr
(0
.]
У
сos Ф
I
A2u
,
02tD
,
:
u
td",
-f
au"
-r
ГОn Оl, ,
ll
x
L7;slllo
+
аУ
сos(D-
Ъsiпtо
l
yсostо
tl '
Оu
,0o
'
zsino
IDс(lsФ
_ ll.
о'
.1-
ag
-г;БinФ
i
!/сusФ
-
"'
'1T
'
dT
гaAT ,
о2T
,
l./ -=--тD.
:ai.
-t-,.
f
о.t
,
og
Loro
o!J.
+ I /{
sin,o
+ {
.o..'ll
.
l
'8rцФ+yсosФ
\o..
oу
lJ
cslnФ+ycosФ
Pяc.
6.4.
сxeпrд
paспpoстpaЕеIlия
cтрfll вдoлЬ
ttol|yoll.
4.4
прп pаосltoтprцIllt
задачII
o свoбoдпоii
всeрllоii
закpyleннoй
cтpye-исToчEиI{e
'
сЛeJlуcт
oтбpoсптr,
в Лcpl]olll
уPцBllcrtиII
cистемьI
",
1 iJp
(o.4/, чЛeЕы-u.IJ
n
--
d:.
Cпстeшa
ypавпeнпй
пoгpаЕиtrвoгo
clloя
(6.47)
дЛя динa}IшIe-
скoй
зaдaчи
дoлrкпа
быть пpoиЕтeтpиpoваIta
IIpи yчeTe
гpaЕпч-
шьIх
yслoвцй:
u:1,:u:0
пpп
y:Q,
t
u:u:0'
пpи y:o6.
J
Поcкoлькy
и
адecь
peчь
tlдeт
o
с1рye.пcтoчEикe'
пeoбxoдимo
lt гpаЕичЕым ycЛoвиям
(6.49)
пpисoeдинцть
инTeIpaлЬнъIe ycлoвия
9
л.
l. вудтс, B.
п. Iinшкflpoв

130
IIoлУoгI,A1llIчЕIlньIЕ стpУI{
I{вс]ItиllAЕl{oЙ 1кl1дкoстIl tIл.6
стPУя
вдOлЬ
пPяпtolo
кPУглoгo
кoIlУсA
13t
(6.53)
Bывoд кoтopЬIх
aEаЛoIичeII
ПрпвeдelrEolty B IIpeдьIl]yщeII
paзделe
(см.
тaкжo
{,02l).
[lолaгaя Kф0 тt Лf 0,
нaйдеlr
ЕeтpllBпaЛьныe
DeIIIeяия.
lloЛoi+iпll' как
ooьfrIEо'
дЛя
peшeEия
диEаnlllчeс}iolt
зaдaчп
(6.52)
u^--
Аx",
a*: Cr",
P--
p^:
paь'
9:
IJtj'tэ,
Пpeoбразуя
с
tloмoщЬю выpажiений
(6.52) ypaвнeнпя
,цIIнa
п-
veскoй
задauи
(6.47),
т-tpиxoдим It систсмc oбыкнoвeнных
диффe-
peEциaЛЬЕьIх
уpаIlllсitrl
jl
:
сoxpa}IeнIIя
D виде
ф1J
\
o,",
(\o,,
ау)ау
:1r:
сortst'
t . г
'
\
'
.'
\
p'",иtа
\
pru
d!
|
dlJ
-
.v сonst.
JJ
00
tu:
t'
ttl,
*:tttl,
ffi
:'1*1,
7-
1-
ItF"
+
2tr"2:0,
I
Р,:
-
с.]l2,
I
(I)"
+,.''Ф, +
2F,Ф
:0
)
с I.pа1lllчllь]м|t
vсJ]ol}}{я\,{II:
]?:F,:ф:Q 11p11
сp=-Q,
l
F,
:Ф:
P:0 lrprr
Q
_
o".
j
Иt сoпоставлeпия
пepвolo
и трeтьeгo ypaвнeний
систeмI,I
п гpaцIIчEьlx yслoвцй
для
функций
Л' и Ф
слcдуeт, lтo
l
11/
lц
-у
l-
\vт
-|/ц),
Ф: n',.
Кpoмe тoro,
3aдача
oTъIскaЕия
фyнкцпи
Л,(9)
aвaлoгиlпа
зaда.
че'
дeтaЛьцo
pассмoTpeннoй
в прeдInдyщel!
pаздe.lre
(o
плoскoй
пo.
луoгpaпиleIrпoй
стpye).
Пoэтoмy pоIxeЕI{e
мo;кeт
бьrть
ЕallисaЕo
оpaзу
i',_Ф:
|{r"*r'n-r,ч,
(6.57)
пpIIчeм
P:""-{ln
-l-
(6.50)
(6.51)
(6.53)
цl.;1)
+
2t/5
(arctg
I+#-
^..,*
#))
(6.5s)
:1,7818).
oкoЕчатeлЬEo
имeeil
дJIя
кoмПoIIeнT
скopoсти
Значонпя кoнcтaпт автoмoдeЛьI]oсTи и ПoсToяЕItInх
А'
B'
с'
D'
troЛучеIlllшe
пptт этoм
пpeoбpaаoванип
уpавнeниiI
It испoJIЬзoвaЕиц
иIITеIpaЛьIIыx инвapиаЕToB (6.50)
и
(6.51)'
oкaзьIваются
paвIII'Iми
3^55"19
а:_
2L,
P:-
n='
t:
-}
'
6:-;'
(6'55)
(кaк и
paпeе,
.Е'oo
Tаким
o6pазoм,
lI
давлеIII,Iя
":
#o't')'
,
:
+B
%ФqI,'_3F),
':
,*"t't
l,
t
(6'5e)
I|12,1rа
.
ЧY.
l}oспoльзyeмcя
пoЛyчerrIlI{мц
BЬlpа)ItcIIIrя}rи
/lJlЯ
кol{пoEeEт
l.|{()|)(X]Tп
для
BьIчltслcЕия
}taссoBolo
расхoда
G, импyльса
r't'1l.уtt
"/".,*
lrolreнтa
цмпyЛьса
,l{
и
пoлногЬ
пoтoкa
кипeтичrскoй
rПl,DI'ItI
It:
ds:2лtrr
з,, a
$
F-'"t.
-
,'п,
F'2
dg
-
r-'/,,
a
Tait?rtс
^
-1/-#,
':fжл'
^
t't,
f
з
\
':
тV
Rтi'1
r I
(6.56)
\
I Fn сlp).
l
tl
(:-
('
\pD
J
г
\
prl
J
Dс
.',r
\
2
сls
:
2лo
sin o
4 r-li i
.Ц.]
0
,. /if\r
цf
зк"
/,
U
\ к.)
(Lg
a
|/ ;э:;i
(/'
:
3
9*

пoJIУoгРAIIIiчЕIiIIьIЕ
стPУи
ЕEсiE(и},IAвмoи'I(идttoсти
tгл.
6
P
'
Аc
',r^'^'
M
-
\pruш
sin 0)ds: 2пp sin2 o:f
g-и
\
F'z
d'p
-
xjп,
.l'
t'
J
s0
д:1(oa'ds:лo,io
l' ., с.,"
'
z
J.
0Dт,,-x\I "аp-I-l..
I{ак
п в
p"абoтe
[oo,],
ono",,"o.'".o
o"сxoдa
Ea
суммapшый
пм-
пyJIьс
G"/I, илп
нa
мo!{eET п}lпyльoa G,Дy',
a
тaкжe пpoиавeдeнпe
вlдa G|E сoхpaвяют
пoстoяЕEoo
аЕачoнпo
Bдoль
стp]rи в
кoцичe-
скEx
ceчoEпях'
opтoтoнальEых к пoвepхЕoсти
кoвyca.
B выбpaвной спстe}te кoopдиЕaт выpaх{eния
для
ltol,lloЕeнт
oкopoстц
сoBпaдаIот с пoЛyчeнными в
paбoтe
М. C.
{yккepa
[з0зl
для
cлyчaя 6,
:
}.
этoт пpедeльпый сл5rraй
oтвeяaeт пстoчeEпю
вeepнoй
вaкpyueнпoй
пoлyoгpапичsвпoй
cтpyи. Пpп
.-*}.pa.
дпoEт дaвлo*ия
пcчoаaeт.
Haлпчиe тpaдпeЕта
давлoEпя
<u*+ol
цpедoтaвЛЯет
xаpaктepпyЮ oсo6eппoсть
pacclrатpивaeмoй
-iaдaви
пpи o
(}.
oбpатпlrся
к
рeIIIeEию
тrплoвoii
зaдаlи. Pассматpивaя
тp!
тПпa
lpaЕпqных
услoвпй
(6.28a
-
в),
зaпишerr
peшeвия ypaBЕo.
Eпя энepгиI!
(6.1r8)
сooтвeтствeцЦo B Bшдe
а)
^?:
гrY0i (q)'
6)
^Z
:
I'1106
(q),
в)
Д?
:
A?'.0" (q).
,(ля
тoгo чтtlбьt паiiтц аBтol oдeJlьIIIne pеIпeЕия ypaвЕeЕпя
эвepгип
(6.48)
с
учoтoм
IpДIII{ЧЦI,IХ
ycЛoвий
(6.28)'
дoпoлним
их
иEтeгpaЛьsымп инBapиантaмц !I
3начeEиямII кoнстaЕTъI
aвтo!,lo-
дeJIьEoотц
T.
сдeлaoм аTo пoслeдoBaтeльEo
для
всeх тpeх впдoв
гpaЕичEьIx
ycлoвий
для
тeмЦepaтypы.
a) Пpи сишrroтpгtlЕьIх IpaЕIlчЕьIх
yслoвпях
для
скopoсти
и
тeмпepaтуpы пpимeм'
кaк п в зaдaчe o плocкoй пoдyoгpaEичoн-
вoй струe,
a
с
'|п,'|.
,
т:сt:_+,
Kт:
\
(^Z),':dy:
сoпst,.
.z'.J'
B чaстцoм слyчae
paBeEстBa
eдицицe
vпсла
Пpандтля'
кaк п въIIIIor
yка;I(eм
TaI{}l(o
выpa)iiellиg
бoЛee oбщeгo
иIrBapпaEтa:
сo
1/
Ki
:
\
pc"u
ЬT
|\pur
dц], t
du
:
сonst.
\J'
"
t
00
6.2] стPyя
вдoлЬ пPямoгo
ltPУглoгo ItoIIУсA
t33
б)
,(ля
вeтeплoпpoвoдпoй стeнки
i'з
o.:2л sinФ\ oс.ш
^r;г
du
:
сonsL.
т:-|.
\o
l.
Р
,
4
d
в)
.(ля
стeнкп
пoстoяццoй
тe}rпepaтypы
,y
:
0.
Пoслe
пepeхoдa к аBтoмoдeЛьЕым
ypaBIIсEI{яll
Ilpихoдим вEoвь
к
тelr я(o oбыкцoвeнным
диффepeнцпaльныIlt
ypдвнeЕпям'
чтo и
для
плoскoй
пoлyoтpаBичeЕЕoй стpyи:
0"
+
pr
(д0"
+
2F,0а): 0,
ollf Pr
(F06)'
:
0,
o"+prлo,:o,
с
тeми ,Ito гpаничньI}tи
услoвиЯмп.
Пoaтoмy
для
вeepнoй пoлyorpa-
пиseннoй стpУп
сoхpaвцтcя
Toт llio вEд
pеr[сний,
чтo и
для
плoс-
кoй.
Hoвыми бyдyт
тoлькo
аЕaчeЕця
IIoстoяIlIIых в
cвяаи с ицыl{
вIlдoм
I.рaвЕeEия
EeпpepьIвEocтЙ'
Bыппrпeм кoЕoчEьte
peзyльтaтьI:
fl)
^r:
Г-5l'-,ю"tql
lIu:l'" 1
(
*'
.
{i;';{I'
r,'ьF,(0)
onи вr:
l),
(6.6r)
(6.60а)
(6.60б)
(6.60в)
l.t
'\/
^7',||
l\..'',I
p.
\l.'а.r).l.r'Iх
I
t.'
'\
:
't 't"
'r'
, ?
-
r
-
t-l)
у
] \
..r1l{-
Pr
\1,.с19 )dq| [.
l.r
_
\
)
t
-J
J
o0
(6.63)
l ll.r.Ily/(rl.l
tIlll((]lIltl.il'гlt
It3]llсtIcllltc пoтoкa избытoчнoтo тeплocФ
,/
( |
|
|
|
, I . l
l
|
|
l |
'
| |l
\,(..l(,IlIl,|х :rirлir.r a) и в):
(')
'
..}п1lсo silt .
{,.и(
F'0dq- т-,t,
0
стPУя
вдoЛь
пoPис'l'oft
стЕтII{и
',у
пoлУoгPAIiичEнIlыЕ сTPУи
I{EожtимAEIшolt}ItиДI{ocти [Iл.6
в
оil\.чae
oдIlнaкoвoй
тelr!пepaTУрьI отeЕкЙ
I{ }tiидкoсtrt
вдaлц
oт
нee
(пprr
".rюбort
знaчeЕии
vислa Pr) и
4Г-т:т
r
Q
n
:
2лpc,,sin to (7',
_
1.
-)
v
#+
x"/,
\
Л',0" dсp
-
r',t
_
IIpII пocтoяEЕoй
тeмпеpатуpe
cтeнктt
(T.
f||l'-).
lToслeдняя
зaви-
сиDlocTЬ
вIIoвь
TaI(аЯ
)кe'
кaк
У
paсхoдa ,fiIIдкocтII в сTpye.
Haкoнeц,
для
сpeднeгo
пo
бoковой
пoвepхнoсTll кoцуса зпаqe-
I]ия чllсЛa Hуссeльтa
пoЛyчим в слуlаe
в)
N u-
:
-
4.B 0;
(0)
/-'l..
Pасclroтpеннaя за,цачa
o
pаопpoстpаEeЕIII{
стpуи
вдoЛЬ
пoBepх-
flостп
кoнyса в пpедeЛьIrом
частIlo}! сJIучаe
утЛa
Прц Bepцjинe
(')
:
;
пepeхoдI{T
в
зaдaчу
o вeepнol.r
lToЛyoгpанпчelrпoir стpye..
Aналoгичньlм обpaзoм
в
pабoтe
Б. П. Устимerrкo
['9.i
pеrпeнa
аaдаqa
o
расцpocтpаIleнии
ЛalIиIrаpнoй
пoJlyoгpallичeEEoй стpyи
вдoлЬ
IlилиIJJIpa
6.3. Cтpt'я в,l1o;I ь пoprrстoir
стсrrкIl
Ii :lа.'1а,ttrlr,
пoдpoбшo
l)ассlIoTprнEы}I
B пpeдьIдУщtrх
раздeЛах'
ПpII]|lInIiа0T задaча o
рас]IpoстpaнеIrI{и
п.цoскoпарaллeЛьнoп лaмЕ-
на1ltlrlii
стрytl
tlссititltttirсмllii
'liидкoсTи'
Bытeкающeй иа
Toвкoй
ще-
Jlи' opllctITIlpoBаrrпoii
по
oсц oz
lт
д(виlкущейся
вдoЛь
IIoристoй плa-
стиtlьt B
ЦаПpаBJteнIIll oсtrт 0э.
l|сpез
IIлaсTIIIly lloлteт oTсaсываTЬ-
оя
?lil{дкoсTь I{3 Iloгpa[Iиtrltoгo
c'ЦoЯ иJIII иIl}I(eктиpoBaтьcя
в Еelo.
Пpимeм, rтo
физиlескиe
свoiiствa
пoдвoдимoй (или oтвoдимoй)
чepeз ПлаcтIlнy rfiидкoсTII
Te
}кe'
чтo ц B стpye. C
вцeцrпeй
сTopoEьI
cтpyи'
IlаIi и
в обычпoй пoлyoгpавпчeEЕori стpye,
Еаxoдцтся
tre.
пoдBи}кная
(нa
бeскoпevвoсти) жидкoсть
тeх яte свofiств.
Peшeнпlo
пoдЛe)I{цт
сцcTeма
ypaBЕeний (6.1) лalll{нapIIoгo
llЛoскolo цoгDaЕичЕoгo сЛoя
Цoй
кonrПoltrнты
скoрoсTи
цpинятa
сTепеЕнaЯ
3авиcиIrroсть
oт
кo.
oDЛиEатьI
lГ.
''.Ь*n"'""""u
усЛoвия'
oбeспeвивающeгo
EeTpпBI{аJIьЕость
реIПe.
o"u,
,"o"*"n,
li"тeгp-аль"oe
yслoвдe'
вьIBoд
кoтopoгo
анaJroгиtlеЕ
BъIвoдУ
ItЕваpиaltтa
^
к ,'дi""
o
oo,yo"p",."o"f"oй
стpye.
,{,ля
".рй"uдo.o."opистоЁ
пластцвъr
тaкoe
yсЛoвиe
иlleeт
вnд
6.31
Кolrпoнeнтьl
Beктopa
скopoстll
запиIЦeм
B
впдe
пeняlr
бeзpазlIepпoгo
пaрa}leaра
g:
q:u'f'
:
qor"
'
кoтoрый
будем
cuитать ДосTаToчEo
мaЛьIпl:
tt:
Аrd
F'o(сф
1qА,r"'F',\сp)
l
,
. .,
А.
u:
u._!;
л.
р-r[(*-I])Fo
*РqЛ"l-
-
tt
}
r",-в-|
t\а.,
_
Р)
F,
+
PqЛ't
-
. .
.
e,!i
+
#
(l:|
r
"r,"
-
аt',;)
_
o'
1в.68)
rt:'
+
#L+
F"F;
3r
.Jу'
\
|
Li i'
-
*hr'":0,
(6.6e)
l}ltitlvtеtl
иптerpальEoтo
yсJIoBия
(6.65)
полyrим
фU*.r
(
u,
(\,
ay)
ay
_
\
a,(\
и, dy)rtr
:
L
:
соnsl.
3
'n'
""
6'
(6.65)
pядoB
IIo
стe.
(6.66)
(6.67)
}tак
и в
дpyгих
слyчaях,
здeсь
9..:
ByzB;
rптpихoм
oбoзнalепo диE.
фepeвuиpoйаниe
Do
дepeме^Eвoй
9.
.__. гI
Лoдcтавим
въlpа]кeвця
цu.ri7)
в
nсхoдвш"
уpullj1]]:
llpиpаB-
''#;;;;;';_io"66"ц".i'.'''p![
oдинакoBыx
стeпeЕях
п-lаpаIr4rт.
pa
q. B
peзyЛьтатo..
tloлJrчц[l
сиЪтeмУ-
обыквозeнвшх
'диффоpeв-
,it'ononn'*.
уpавнeвий
для
ollpeдеЛeвия фуЕIIцпII
f0.
дl'....
F
(x
+
1)F';Лi]
_
0u Оu О2u
0ц
'
1tl
U-
i
?-:V-.
--
-l-
-
:U.
o'
oll o.It" or ' oу
llpи сJlсдУющих
IpaEичнInx
yсJIoBиях:
и
-
0'
U
:
ul.:u'0rx пpп
t/
-
0,
,l
u.. o
"p"
o-
*.
I
Tакltl't oбpaзoм,
Еа
пoвepхнoста
пopистoй пластиriы'
дa'
пpoдoЛьIrаЯ кoмДoнeEтa скopoсти
paвEa EyJIю;
дЛя
(6.1)
(6.64)
кaк
всeг-
пoцepeч-
д,,*
\
лf
(\
л"
аy1
ay
:
r,
00
(6.70)

r36
E
пoJIУoгPAIiичвIlIlьIЕ
стPУи
IIEс}киl[AЕмot
Etl(дкocти
(6.71)
Пpи вывoдe
ypaвнeний
ц
цнтeГpалЬEыx
услoвпit
былo
пpцнятo
p:+,
d,:)
(в.72)
Иа
paвeпcтва
(6.70)
ииeeм,
кpoмo
тoгo'
3"
:
2p.
Taкпlr
oбpa-
аoir' пoJIJпIae}l
":-+'
р:_+'
o,:+.
floлotхпм
такяte
o:
+(+)''",
u
:+(*)\,
r,
:+#(*)'^,
пoслc чeгo ypaвIIеIIп,Il
lpallичшIne
п
пIlтeгpaЛьныe
yслoвиЯ
дJIя
ЕyЛcaoro
ltpIrб;rиlrrelил
бy;1yт
имeть
впд
F:
I
FoF;+2F;:0,
&:F';:0
пpп
9:
0,
д":o
(6.77)
l_чi..o.l.lo
атollly
для
пepвoгo
пpпбли)I{eEпя'
ttoтopьI}t
п oгpaEп.
чи}tся'
oудei{
пмeть
F|
+
F"Fi+(1
_4х,)FьF|+4(1
+х,')F;h:4F;,
(6.7s)
6.3]
стPУя
вДoЛъ пoPистoи
стEЕl{и
|37
Peшeциe
ypaвнeнпя
l{yJIeвoгo пpпближeяпя
пpп
сooтвoтствyю.
щих
гpаItцчIlЬIx
ycлoвIlях
иtвecтEo (см. paздeл
6.1):
'
e
z3\
(zz
:
:!-\. 1
Fo:iFЗ";(-,.,
\
JоmJ
I
1
,
1Iz#z''
|Б . tT." l
(6.81)
q
:
,j'
rll
_п_-j'-
+
;;-
aтсLg
i
-;.
I
-.
0сo
.
0oo
'
Cлeдoвaтeльнo,
кoаффпциeпты в
уpаBEeEпц
пepвoгo
щlибли-
жепия
(6.78)
oпpeдeЛoЕъI. Пpoизвoльным
oстaeтcя зЕaчoпI{e кoЕ.
cтаптьI
x (пoкaзaтeля
стeпeпи в
taкoнe
oтсoсa
пли вдyва).
B кaчeствe пpoстeйпreгo
чаcтEoгo
сл}пIая пp!мeм z
:
0.
Этo
сooTвeтствyeт пoстoяЕцoй BдoлЬ
плacтЕЕьI
пЕтeЕcпвЕoстп oтсoca
IlлI{ вдyBa.
Уpaвнeвиe (6.78)
пpи атoм пpиEиllaeт вид
F';'
+
F"F:
r
F'nr',1 4F;Fr: 4i;.
(6.s2)
Пepeirдeм
к пoвol.t нозависимoii ПepeмeЕЕoй
zцz2
:
.!!)
ваaмoн
9.
IIoслe
этoгo'
aвaлoгиtlнo
paбoтe
[r9l,
цo..ryчиt,r
fi,u'"'""
(пrтрих
_
диффepeнцпрoвaниe
пo
z)
(1
-
zв1zp"'
,",
_6z2
(7
_
zg)
F,;
G\
+
24(1
_
4z3\ F1(z)
:
:24(r
-
4zs)
(6.83)
с гpaЕпчEьIldи
услoBиямп:
F',: Fi:O
пpи
z
:
0,
}
lim(1
_z3)n'i(z):0
пplr z---1.
J
ч1lфu
,4
rrl",",
\
ri
(\
ri ау)
а
у
+
2,l,xz"-",
l
r
sli (\
r;
а
у1
а
o
-
{,о""-u
rP
-
* \,,. I\
Fitlц1du
:0.
v-
J
\J
-
"/
-
00
Пpп
9:
oo'
('-
-{
-
\
f'nf;
dФ:
1.
.)
--
0
(6.73)
(6.74)
(6.84)
Уpaвнeвиe
(6.83) пмeeт
oсoбyю
тouку
apД z
:1.
Пoэтoмy
peIпe-
ttио
eгo
бyдeм пскaть
слeдyющцм oбpавoм. Пocкoлькy Еa
8Еaчи.
l'oJIьEoм ytlacткo
памeЕ€Ilия z' напpимoр пpи
0ч{z(0,9, oсoбых
.l.()llск
цетl pelцeниo
уравЕeEпя
(6.83),
кoтopoe lfo}riЕo прeдстaBитЬ
l|
lllIл0
t(
-
zз1z
p,,',
:
24 (1
-
izx) (1
-
F
]'
(6.83а)
|Irlii;lcм
мeтoдoll
пoолeдoвaTc.ll,llых прпб.rпrкeuий (кaк
в
paбoтe
|.''l).
lJблпзu тoчкII z:1 prltошие
эTol.o ,I{c
урaвEeЕия
пщoм в
ltl|/l(!
р'Il(а
IIo
стeпcllяIrr
1
-
z,
С
yчrToм
вTорoIo гpallичнoгo
ycлo-
ttttll ((i.8/r)
oбщеe
perпeниe
дЛя
)пIaстка
0'9
(
z
(
1 пмeeт впд
/,',(:)
1
+
с,Г1
-
z-2(7_z\2
+ 1tt_"v
_L(1_z)a+...l-r-
-'-,1-
-r
'
3\-
-,'
3\-
-t
t...ll
|,',
Il
r
- z
!
2
(r
-
z)2
+
I |
-
")"
-
| ir
-
r1n'l
ro
(
-
z)
+
-r[
'J
tl
I
t 4(t
-z\2
-3.16611
-z)3-f
1.638(1-z)a+.
lln
'| ,{
_(tr.s5)
(6.75)
)
t''u'
(6.7e)
(6.80)
оo
