Войтенко C.П. Математична обробка геодезичних вимірів. Теорія похибок вимірів
Подождите немного. Документ загружается.


Якщо г > 0, то маємо позитивну кореляцію, тобто із збільшенням
абсциси х, збільшується величина ординати у (рис.3.3,а) і навпаки
при г < 0 .
Якщо випадкові величини X і У незалежні, то кореляційний момент
і коефіцієнт кореляції дорівнює нулю, тобто К
ху
= 0 і г
ху
= 0.
Дві корельовані випадкові величини завжди є взаємозалежними, але
дві залежні величини не завади є корельованими. Прикладом цього може
бути система випадкових величин (X, У) рівномірно розподілена в межах
кола з центром на початку координат. Розрахунки показують, що·
величини і У залежні, а кореляційний момент К
ху
= 0, а це означає, що
і г
ху
=0 [15, с.125].
Випадкові величини X і У називають корельованими, якщо
і
г
ху\
>
0 і при г
ху
0 - некорельованими.
Коли коефіцієнт кореляції дорівнює+1 чи -1, то між величинами
Хі У існує прямолінійна залежність у вигляді рівняння прямої
V = ах + Ь.
Форма прямолінійного зв'язку між випадковими величинами X і У
визначається у вигляді рівняння регресії У на X:
уМ
у
+ р
}!
(х М
х
), (3.25),
X на У
х=М
х
+ р
х/
(у-Ц,). (3.26)|
/у
Коефіцієнти регресії р
у
і р
х
визначають за формулами
/х У
Оу ст
г
1
Ру —; Р
х
= (3.27>
' х <*х -У Яу
де значення г, ст., обчислюють за формулами (2.28), (3.24).
Приклад
1.
Для системи випадкових величин (х, = 1; х
;
= 2; = 3;
;
Хі = 4; >'і = 0,8; у
2
= 2,1; у
3
= 2,7; у^ = 4,2) при ймовірностях їх появи·
Р
х
=0,25; Р
у
=0,25 знайти;
*> У,
К
а) початкові моменти першого порядку при 5 = 1, д = 0 і з = 0, д= 1;
б) центральні моменти при 5 = 2, д = 0 і і = 0, д = 2;
82

и) обчислити кореляційний момент та коефіцієнт кореляції
т)
зтйти рівняння регресії У та X
Розв'язання, з) Початковими моментами величин X та У будуть їх
математичні сподівання За формулами (3,14), (3.15) та (2.15)
обчислюємо.
4
а
га
= М
х
= = 1 0,25+2-0,25 +3-0,25+4-0,25 = 2,5;
1
4
«01 " М- = 2 У
і Л>,
=
°'
8
· °'
25 +
2'
1
•
°'
25 + 2
>
7
' °>
25 + 4
>
2
· °'
25 = 2
'
45
'
1
б) Центральні моменти при і = 2, </
=
0 і 5 = 0, ^=2 обчислюють
за формулами (3.19), (3.20) та (2.27):
4
Изо = £,= ][)(*,- М
Х[
)
2
Р
Х<
= [(-1,5)
2
+ (-0,5)
2
+ (0,5)
2
- (1,5)
2
] * 0,25 = 1,25:
]
4
М02
- = - А/
л
)
2
Р
Л
- [(-1,65)
г
+
(-0,35)4
(0,25)* +
(1,75)
2
] 025 = 1,46.
і
в) Для визначення кореляційного моменту за формулою (3.22)
обчислимо Р ймовірності прийняття системою (х, у) значень (х„ у,).
Так як випадкові величини X та У з'являються одночасно і мають
оонакові значення ймовірностей Р
х>
= 0,25 і Р
у
= 0,25, то за формулою
ообутку ймовірностей маємо
Р
ХіУі
= Р
Хі
•
Р
ь
= 0,25
·
0,25 = 0,062.
І оді
4
(і,: =Л;
у
=£О
г
-М
х
)(у,-М
у
)Р
щ
= [(-1,5)(-1,65)+ (-0,5Х-0.35) +
і
^ 0,5 0,25 + 1,5 · 1,75] · 0,062 = 0,33.
В пункті б) знайдено О
х
і О
у
, тоді стандарти будуть дорівнювати:
Коефіцієнт кореляції дорівнює
Кху _ 0,33
а
х
а
у
1,11,2
= 0,25.
83

г) За формулою (3.27) визначимо коефіцієнт регресії
9
у
, = 0,25^ =0,27.
у
х ІД
Тоді рівняння регресії визначиться за формулою (3.25)
у = 2,45 + 0,27 (х - 2,5),
або у = 0,27х + 1,77.
Приклад 2. Випадкові величини X і У незалежні Чому дорівнкі
кореляційний момент К
ху
=
?
Розв 'язання. Розкриємо дужки в формулі (3.21) і отримаємо
К
ху
= М[(Х- М
Х
)(У- М
у
)] -=М[Х
-
У-X -Му- М
х
М
у
] -
=- М
ху
- МгМу-М
х
Му + МгМ7= М
ху
- М
х
Му.
Тоді кореляційний момент можна записати у вигляді
К
ху
= М
ху
-М
х
Му. (3.28)
Згідно з властивостями математичного сподівання добутку два
незалежних випадкових величин (2.21) маємо М (х -у) ~ М
х
•
М
у
.
Тоді кореляційний момент у формулі (3.28) для незалежних величин І
і У буде
к
іу
= М
х
Му -М
Х
М
У
=0.
Приклад 3. Між випадковими величинами X і У системи (х,у)'
кореляційний зв 'язок у вигляді у = ах + Ь. Довести, що при цьол
коефіцієнт кореляції
{
г] = 1.
Розв'язання. Згідно з властивостями математичного сподівані
(§ 3, розд.2) визначимо математичне сподівання функції у
М
у
= М {ах+ Ь] = аМ
х
+
Ь.
За формулою (3.21) обчислимо кореляційний момент
Кху = М[(х- М
х
) (у - М
у
)] =М[(х-М
х
)(ах+Х-аМ
х
-М =
1
= аМ [(х - М
х
) (х - М
х
)} = аМ [(х-М
х
)
2
}- аВ
х
= а0
2
х
.
84

За формулою (3.24) коефіцієнт кореляції буде дорівнювати
К
r
xy =
ХУ
у
аа:
о
х
о
у
Із рівняння у — ах + b визначимо стандарт функції у, виходячи з
властивостей дисперсії (§ 3. розд.2) D
y
= О
2
D
x
і
<J
V
—
ats
x
.
Тоді
Г -
' ху
аО
у
Ох
а
°х
а
+
1
-1
при
при
а>
О
а <
О
§ 4. Багатовимірний розподіл. Числові характеристики
системи довільного числа випадкових величин
Якщо система включає більше двох величин, то її розглядають як
випадкові точки або випадкові вектори в просторі відповідної кількості
и-вимірів.
Повною характеристикою системи и-випадкових величин
(Х\, Х
2
, ..., Х„) є закон розподілу цієї системи. Його задають функцією
розподілу або щільністю розподілу.
Функцію п-аргументів х\, х% ..., х
п
, що дорівнює ймовірності
спільного виконання п-нерівностей X, < х, (і = 1,п) називають
функцією розподілу системи
(.X),
Х
2
,..., Х„), тобто
F(x
h
х
ь
..., х„) = Р(Х
1
<х
и
Х
2
< х
2
, ..., Х
п
<
х„).
(3.29)
Граничне відношення ймовірності появи системи
№. AS, ...,Х„) в невеликих межах навколо точки (jf[, х
2
, ..., jr
n
) до
розміру інтервалу межі при необмеженому його зменшенні
називають щільністю розподілу ф(хі, ..., х„) системи п
випадкових величин
ФІЛ, **.... *„) = Я (3.30)
дх
}
,дх
2
, дх
п
85

Якщо закон розподілу системи «-випадкових величин (Х\, Хі, •••, Х„)
невідомий, то її характеризують числовими характеристиками:
1. Математичним сподіванням М.
М
Т
=
м
х
\
х
п у
(3-31)
де М
х
_ - обчислюються за формулами (2.15 - 2.17).
2. Дисперсією О
х
О
х
=
о.
*2
А,
(3.32)
Дисперсії характеризують міру точності кожної з випадкових
величин, тобто розсіювання випадкової точки в напрямку осей і
обчислюються за формулами (2.26 - 2.28),
3. Кореляційною матрицею К
х
Вона є узагальненим поняггям дисперсії Д
г
для випадкового
вектора X Визначається за формулою
К
х
= М[(Х М
х
)(Х-М
х
)
г
).
(3.33)
Відомо, що математичне сподівання випадкової матриці є матриця,
складена із математичних сподівань її елементів. У формулі (3.33)
приймемо п = 3, отримаємо
К
Х
= М
(*і - М
Хі
)
(х
2
- ) (х, - М
ХЛ
) (х
2
- М
хг
) С*
3
- )
х
2
86
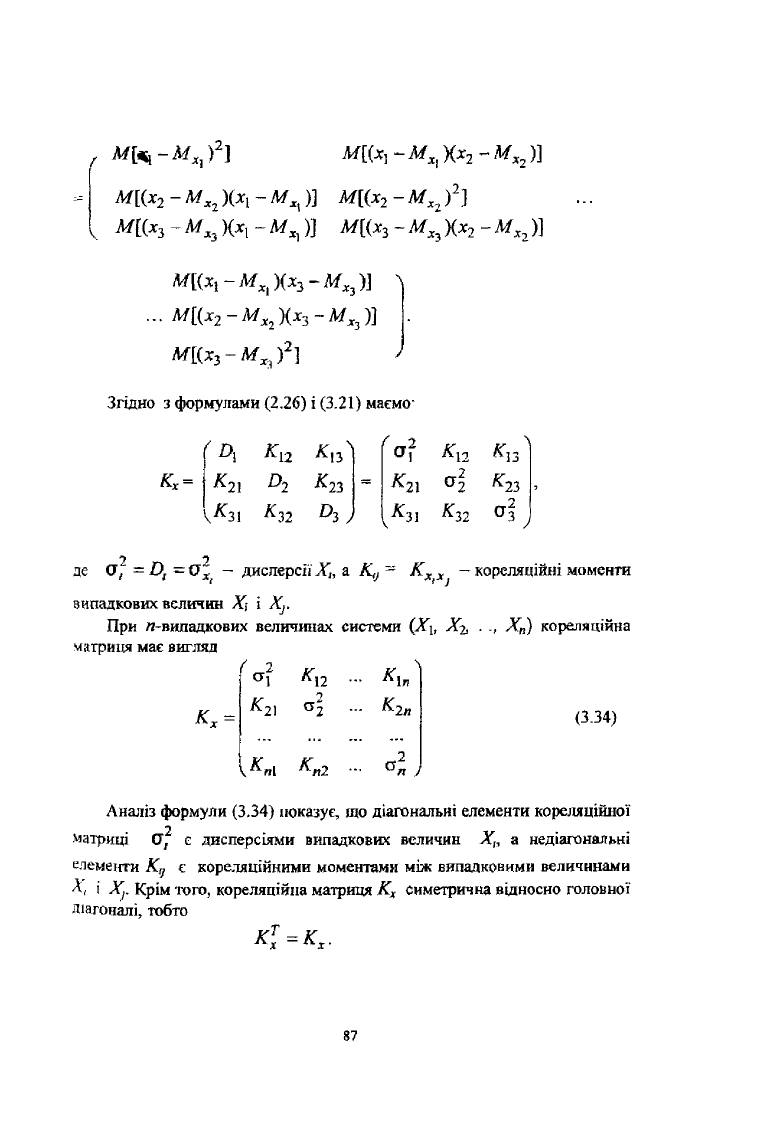
М[{х,-М
х
Чх
2
-М
х
Л
М[(Х
2
- М
Хг
)(*!
- М
Х{
)] М[(х
2
- М
Хг
)
2
]
^ )(х, - М
Х]
)] М[(х
3
- М
ху
)(х
7
- М
Хг
)]
М[(х
х
-М
Хі
)(х^М
Хі
)]
-
МІІхі-М^ІХІ-М^)}
Згідно з формулами (2.26) і (3.21) маємо
ҐА
К
12
Ґ 2
Ку)
II
к
2
, о
2
К-21
=
К
2\
оі
^23
ч^ЗІ
К
32
Б,)
К
12
2
2
де О, = О, = О
х
- дисперсії Х„ а - К
Х<Х]
—
кореляційні моменти
випадкових величин X; і X).
При «-випадкових величинах системи (Х\, Х% . , Х
п
) кореляційна
матриця має вигляд
'гг
2
К
г
—
К,
12
«І
К
2
1
&2п
(3.34)
Аналіз формули (3.34) показує, що діагональні елементи кореляційної
матриці О
2
є дисперсіями випадкових величин Х„ а недіагональкі
елементи К
ч
є кореляційними моментами між випадковими величинами
А і Х
г
Крім того, кореляційна матриця К
х
симетрична відносно головної
Діагоналі, тобто
Кх = •
87
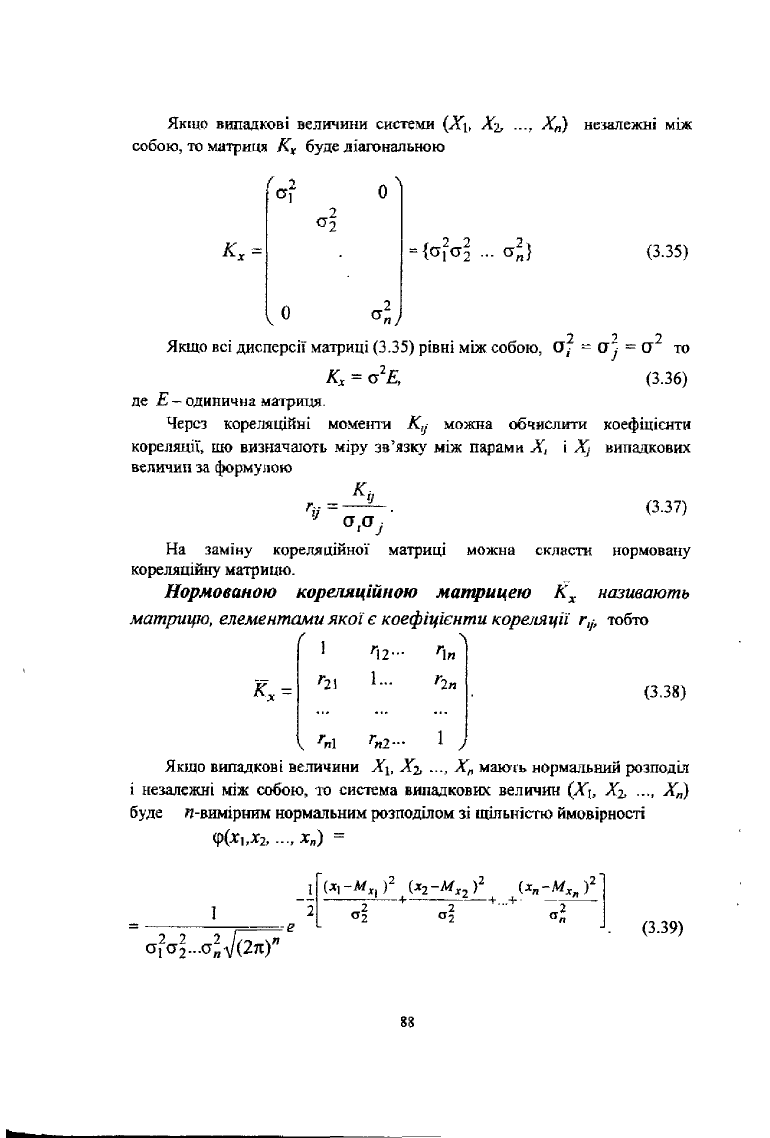
Якщо випадкові величини системи (Х\, .... Х„) незалежні між
собою, то матриця К
х
буде діагональною
{ "І
®Г
к
г
=
4
(3.35)
2 *) 2
Якщо всі дисперсії матриці (3.35) рівні між собою, О
і
" = О то
К
х
= о
2
£, (3.36)
де Е - одинична матриця.
Через кореляційні моменти Ку можна обчислити коефіцієнти
кореляції, що визначають міру зв'язку між парами X, і Х
і
випадкових
величин за формулою
г
9 =
К
н
0
^'
J
j
(3.37)
На заміну кореляційної матриці можна скласти нормовану
кореляційну матрицю.
Нормованою кореляційною матрицею К
х
називають
матрицю, елементами якої є коефіцієнти кореляції г
ч
, тобто
і /·,,... г
и
г
г\
'12-
1...
'їй
'2л
(3.38)
Л.1
Г
П2-
1
у
Якщо випадкові величини Л\, ..., Х„ маюгь нормальний розподіл
і незалежні між собою, то система випадкових величин (Ху, Х
ь
..., Х
п
)
буде и-вимірним нормальним розподілом зі щільністю ймовірності
«І
а
2
(3.39)

Щільність нормального розподілу для системи двох залежних величин
X і У буде
Ф.У) =
2па
20-4)
(х-М
х
)
2
ІУ-МуУ*
л
(х-М.Ху-Му)}
„2 2
2Г
*У —
1
-л
(3.40)
ху
Як видно із формули (3.40), для двох залежних випадкових величин
закон розподілу визначається п'ятьма параметрами: М
х
, Му, с
х
, а
у
і г
ху
.
Формула щільності нормального розподілу для системи
(Х-, Хь Х
п
) залежних випадкових величин Х\, Хь ..., Х„ має досить
складний вигляд.
§ 5. Функції випадкових величин. Числові характеристики.
Кореляційна матриця системи функцій випадкових
величин
В практиці геодезичних вимірювань виникають задачі оцінки
точності результатів, що є функціями однієї чи декількох виміряних
величин. Отримані функції теж будуть випадковими величинами. Як
правило, відомо закон розподілу системи випадкових аргументів і відома
функціональна залежність. Тобто, є система випадкових величин
(Х\, Хь ••·, Х
п
) і закон їх розподілу. Розглянемо функцію У від
випадкових величин^, Х
2
, Х„
У=ЯХ
1
,Хь...,Х
П
). (3.41)
Практично вирішують зад&чу визначення закону розподілу
випадкової величини У, виходячи з функції (3.39) і закону сумісного
розподілу її аргументівХ
ь
Х
2
, ..., Х„.
Покажемо вирішення цієї задачі для двох випадкових величин. Маємо
функцію
Очевидно, що щільність розподілу системи випадкових величин
(Л'ь Х
2
) буде - <р(хь х
2
).
Штучно введемо нову величину Уі = Хі і розглянемо систему
Двох рівнянь
У = /(х1,^2 X
У\
=
*і
(3.42)
89

Очевидно, цю систему можна однозначно визначити відносно
X]
та х
2
,
тоді
*2 = ЛУ>У\)
(3.43)
Виходячи з того, що система (3.43) диференціюється в теорії
ймовірностей, доводиться, що щільність розподілу випадкової величини
у — Дхі, х
2
) в нескінченних межах буде
ф(У) = і ф[*іф ,У.*І)]
дфО%*і)
ду
сіх,.
(3.44)
За аналогією находять щільність розподілу для функції трьох і більше
випадкових величин. Наприклад, якщо У
—
Дх
1(
х
2
, Хз), вводять нові
перемінні
У^Х
ь
Уг
=
Хг.
Якщо при цьому між системами (А\, Х
2
, і (У, У\, У
2
)
виявляється однозначне співвідношення, то щільність розподілу
випадкової величини У буде
ф(у)= І І Ф[хіЛ, ФО'.ХІЛ)]
дц>(у,х
ь
х
2
)
ду
сЬ
х
(іх
2
, (3.45)'
де ф(у, Хі, Хг) - зворотня функція.
На основі формули (3.44) визначають щільність розподілу для
випадкових величин: у = (хі + Хі У, У
=
(хі - х
2
У, у - хі • х
2
та
у = ^ [8; 15].
х
2
Наприклад. Закон розподілу величини відхилення випадкової точки
(X,
У)
від початку координат при умові, що система випадкових величин
(X,У) має нормальний розподіл з параметрами М
Х
= М
У
= 0 і о
І
=о
)
= о
називають розподілом Релея.
Зазначимо, що щільність розподілу такої системи (X, У) має вигляд
ФС^У)
1
2л <т
2
7 "»
' 2а
2
90

Відхилення точки (х,у) від початку координат буде визначатися
випадковим Лектором R, що є функцією випадкових величин X та
У,
тобто
r = ^x
2
+y
2
.
Випадкова величини R є полярним радіусом, тоді
х = r cos 0;
у = r sin 0.
Щільність розподілу ф(>,9) системи випадкових величин (R, 0)
визначають через щільність розподілу ф(х, у) системи (X, У).
Внаслідок математичних перетворень щільність розподілу випадкової
величини R визначається розподілом Релея за формулою
ф (г) =
2ст
о
при г> 0;
при г< 0.
(3.46)
Графік розподілу Релея показано на рис. 3.4
> г
Рис. 3.4
При дослідженнях не завжди виникає необхідність у визначенні
закону розподілу функції випадкових величин. Тоді обчислюють числові
характеристики функції випадкових величин: математичне сподівання та
дисперсію.
Математичне сподівання
функції
випадкових величин
Якщо маємо функцію у = / (Хі, Х
2
, .... Х„), то для системи
випадкових величин (.V]. Х^.-: Хп) визначають математичне сподівання
(3.31) кожної випадкової величини Х\,
Х->,
..., Х„ за формулами
(2 15 - 2.17).
91
