Войтенко C.П. Математична обробка геодезичних вимірів. Теорія похибок вимірів
Подождите немного. Документ загружается.


Оцінкою невідомого параметра а буде
а = Х = (
4Л8
>
І=1
Таким чином надійним значенням параметра а буде проста
арифметична середина х із результатів експерименту.
Приклад 2. Згідно з умовами прикладу 1 результати вибірки
підпорядковуються закону нормального розподілу. Необхідно визначити .
2
оцінки а\ — М
х
, а
2
— о , що характеризують величину і дисперсію
вибірки.
Розв'язання. Згідно з формулою щільності закону нормального
розподілу з параметрами сі] = М
х
і а
2
=
<у
2
для кожної випадкової
величини X, функція правдоподібності буде
Ц =Ф„а
1
,а
2
)= г— .— є
2 202
,
л/2іт ^а
2
а для всієї вибірки
2„ 2а,
Згідно з формулою (4.17) отримаємо два рівняння і прирівняємо їх до.
нуля
п
Я1
, £(*.·-«!)
і
= ()
дв] а
2
д\пЬ
=
п
5а
2
2 а
2
2 а
2
або
у(
х
і-
а
\)/
= 0
.
4-і /а- '•
|=ї
1
а)
(4.19)
б)
а-.
112

Із сумісного їх розв 'язання отримаємо
п
5;
=
Л>І=1—
(4.20)
П
3
2
= сг
2
= Д. = М (4.21)
п
Як видно, перший параметр буде простою арифметичною серединою
х (формула 4.18), а другий параметр буде статистичною дисперсією (§ 4;
розд.4)
Проте виявляється, що при невідомому значенні істинного
(ймовірного) значення шуканої випадкової величини X оцінка дисперсії
буде дещо змішеною. Тому при заміні математичного сподівання М
х
простою арифметичною серединою х незміщеною оцінкою дисперсії буде
В математичній обробці результатів вимірів вираз (4.21)
називають формулою Гаусса, а (4 22) - формулою Бесселя
Метод максимальної правдоподібності приводить до визначення
досить доброякісних оцінок, хоч іноді і зміщених. Проте практично
можуть виникати досить складні системи рівнянь.
§ 4. Числові характеристики статистичного розподілу
Закон розподілу випадкової величини X характеризує її з імовірної
точки зору. Між тим при вирішенні багатьох практичних задач достатньо
знати тільки окремі її числові характеристики, що відображають найбільш
істотні риси розподілу випадкової величини.
Ми уже познайомилися з основними числовими характеристиками
випадкових величин: математичним сподіванням, дисперсією,
початковими та центральними моментами, асиметрією та ексцесом.
Для статистичного розподілу існують такі ж самі числові
характеристики. Справа зводиться до того, щоб за результатами
експериментів знайти формули їх обчислень.
(4.22)
113

Так аналогічно для математичного сподівання випадкової величини
X є середнє арифметичне результатів спостережень х випадкової
величини, біля якого групуються її можливі значення
М;=Х = ^, (4.23)
м
п
де
Хі
- значення випадкової величини в кожному /-у досліді;
п - кількість дослідів.
Величину X називають статистичним середнім
випадкової величини X. Слід зазначити, що при досить великій кількості
дослідів п статистичне середнє М* або X наближається до
математичного сподівання випадкової величини X і може бути прийнятим
замість нього, тобто
м*= ь м
х
.
Аналогією дисперсії випадкової величини X є статистична
дисперсія, що обчислюється за формулою
п
В методі моментів обчислюють статистичні початкові та
центральні моменти будь-якого порядку за формулами:
я
«5=1
(4.25)
У іїііЖ. (4.26)
Й (п-1)
Для статистичного ряду розбитого на групи, тобто для статистичної
сукупності маємо
* І к
0-5= £ v
ί
.χ
i
S
/Z
v
ί; (4.27)
/=[ / м
ЧІХі-Х? (4.28)
і=І / г=1
114

де V , - кількість результатів в /-й групі,
Х
1
- статистичне середнє /-оі фупи,
X - загальне статистичне середнє
Аналіз формул (4 20), (4 21) і (4 22) показує, що середнє
арифметичне X » М
х
, а статистична дисперсія т а О
х
, тобто вони
будуть найбільш вірогідними оцінками параметрів закону нормального
розподілу
Слід зазначити, що при виведенні формул в ММП виходили з того,
що результати експерименту незалежні і проводились в однакових
умовах Тобто комплекс умов об'єкт, суб'єкт, прилад, зовнішнє
середовище і метод вимірювання були незмінними Такі виміри
називають рівнопіочними При цьому дисперсії окремих вимірів будуть
2 2 2 2
однаковими, тобто и, -
<3
у
або т, = т
]
Це дозволяє нам стверджувати, що при рівноточних вимірах
найближчим до істинного значенням вимірюваної величини є середнє
арифметичне X (формула 4 20), а значенням дисперсії буде
£>* т
2
(формули 4 21 та 4 22)
1
[роте на практиці не завжди можна зберегти незмінність
комплексу умов Тоді кожен результат експерименту буде дещо
відрізнятися за точністю і кожній випадковій величині х, буде
відповідати своя дисперсія тобто статистичний ряд буде мати
вигляд
Хь Хі, , х*,
о?,аІ .., ст
2
(4 29)
т 2 , 2
1
акл виміри, коли дисперсії <т, ^ аназивають нершюточиими.
Для визначення приблизних значень вимірюваної величини та
2 2
дисперсії при нерівноточних вимірах, виходячи з того, що о, ^ о^.
систему рівнянь (4 19) запишемо у вигляді
п
-аО/о; =0,
/=1
І>, -ї,)
2
(4 30)
115

В теорії математичної обробки при нерівноточних вимірах ввс
поняття ваги, тобто
1
де р, - вага виміру або вага випадкової величини х,. Тоді статистичну
(4.29) можна переписати у вигляді
Хи Хіі • • -і Хт
Рь Рь -, р
я
.
Вага р, буде характеризувати міру відносної точності резулі
експериментів. При цьому їх можна збільшувати чи зменшував
однакове число С. Тоді формула (4.31) буде
С
а
2
Для спрощення вводять поняття середнього квадратичного відхід
одиниці ваги - = \ІС. Тоді вага буде обчислюватися за формулою;
2
„ ^
Р, =3".
а систему рівнянь (4.30) можна переписати у вигляді:
^ ц
2
І
.2
,=1 Ц
Із їх сумісного розв'язання знаходять формули обчислення за
арифметичної середини X і середнього квадратичного відХ
одиниці ваги:
іґі ІРІ
,=і
и
116

2 ~
Очевидно оцінка дисперсії одиниці ваги р, ~ и
х
буде зміщеною. За
аналогією з формулою (4.22), незміщеною оцінкою дисперсії одиниці ваги
при нерівноточних вимірах буде
Й («"І)
Статистичною оцінкою стандарту або середнього квадратичного
відхилення а буде середня квадратична похибка
т = а* ~ ^ІБ* . (4.38)
При відомому істинному значенні X визначуваної величини а її
обчислюють за формулою Гаусса
'
Я
.ШШ. (4.39)
V п
Якщо істинне значення визначуваної величини невідоме, то
застосовують формулу Бесселя
ш.^Ш. (4.40,
V л-1
де X - середнє арифметичне;
п - число результатів експерименту.
Додатковими статистичними характеристиками нормального закону
розподілу є асиметрія та ексцес.
Асиметрія - це нормований центральний момент третього
порядку, тобто
(4
-
4і)
т
Ексцесе мірою крутизни і визначається за формулою
*
Ек - --
4
г-3, (4.42)
т
- «і^; •
! І""
1
) Т
117

Приклад 1. В табл. 4.3 приведені результати експерименту пр
дослідженні випадкової величини X. Визначити числові характеристик
статистичного розподілу: \і*
х
, 0*
х
, ' Из- 4
Таблиця 4.
1
2
3
4
5 6
"і
7;
х,
-10
+4
-1
+4 +12
Розв'язання. За формулами (4.10) - (4.13) отримаємо:
ц*= X = (-10-2 + 4-1 +4 + 12+ 9)/7 = + 2;
П*
х
= {(-10 - 2)
2
+ (-2 +2)
2
+ (4 - 2)
2
+ (-1 - 2)
2
+ (4 - 2)
2
+
+(12- 2)
2
+(9-2)
2
}/7 = 310/7 = 44,3;
«2 = {(-10)
2
+ (-2)
2
+ 4
2
+ (-1)
2
+ 4
2
+ 12
2
+ 9
2
} / 7 - 51,7;
Цз = {(-12)
3
+ О
3
+ 2
3
+ (-З)
3
+ 2
3
+ 10
3
+ 7
3
} / 7 = 444,9.
Приклад 2. /з статистичного ряду отримано статисти<
сукупність (табл.4.4, рядки 1-7). Обчислити статистичний початко<
момент першого порядку
(X*
ота дисперсію другого порядку
Таблиц»!
і
№ групи
1
-10
2 3 4
5
6
2 Граничні
значення
от
1
-10
-5
0
5 10 15
2 Граничні
значення
до
-5
0 Г~+5 10 15 20
3
Частота V,
2
7
11
14
5
1
4
4
Середні X,
-7,5 -2,5 +2,5
+7,5
+12,5
+17,5
І
5
у,Х,
-15 -17,5
+27,5 +105,0
62,5 17,5
її
6
ІХІ-Х)
-12
-7
-2 +3 +8
+13
7
288
343
44
126
320
169
1
Розв'язання. В рядку 5 визначають загальне середнє статичне. Я
= 180, mo за формулою (4.14) обчислюємо:
118
і
j

1 _
Потім обчислюють відхилення середніх груш Х
1
від загального
середнього статистичного X. X = 4.5. В рядку 7 обчислюють
6
^ГУДХ, X) = 1290. Той/ статистична дисперсія буде дорівнювати
]
* т^І* 1290
Ut = jJ
r
— = j.
'
2
40
Для системи двох випадкових величин (X, Y)
Числові характеристики визначають за результатами «-незалежних
дослідів, які виконують в однакових умовах за значеннями:
X
—>
Х\, х
2
, ••., х„;
У->УиУ2, -, Уп-
В свою чергу системи випадкових величин (х>,}·)) незалежні, а
математичні сподівання, дисперсії і кореляційні моменти будуть однакові,
тобто
К
=м
*> К, =
м
у>
D
x,=
D
U d;, - п;
;
К*
ХіУі
---.г
ху
.
Виходячи з того, що випадкові величини X і Y та система (X, V)
підкоряються нормальному закону розподілу, а математичні сподівання
М*
х
і М
у
та дисперсії D* і D
y
є характеристиками окремих
випадкових величин X і Y із системи (X, Y), то згідно з формулами
(4.20)1(4.22) маємо:
М*
х
=Х = (4.43)
К
=г=
І-> t
4
-
44
)
,=і
п
119

п
— 1
і=1
о:
(4.4
(4.4
;=1
Незміщена та обґрунтована оцінка кореляційного моменту К
системи випадкових величин (X, У) визначається за формулою
1 "
(4.-4
Статистичний коефіцієнт кореляції ґ
ху
обчислюють за формулою
К
^(х
г
-Х)(
Уі
-У)
Ґ — Г
*У „ і
т
х
т
у
(п -\)т
х
т
х у
де т
х
та т
у
обчислюють за формулами
т.
(4.4
Ы
Коефіцієнт кореляції г* знаходиться в межах
Якщо коефіцієнт кореляції близький до ±1, то між випадкові
величинами існує прямолінійний зв'язок. Рівняння регресії визначаюіі
формулами
У = У + р
у
{х,-Х)
або
у
<*1
де
Ру =г
*
т
У
*
т
х · ···«
р
х
- г - коефіцієнти регресії.'
У лі»
120
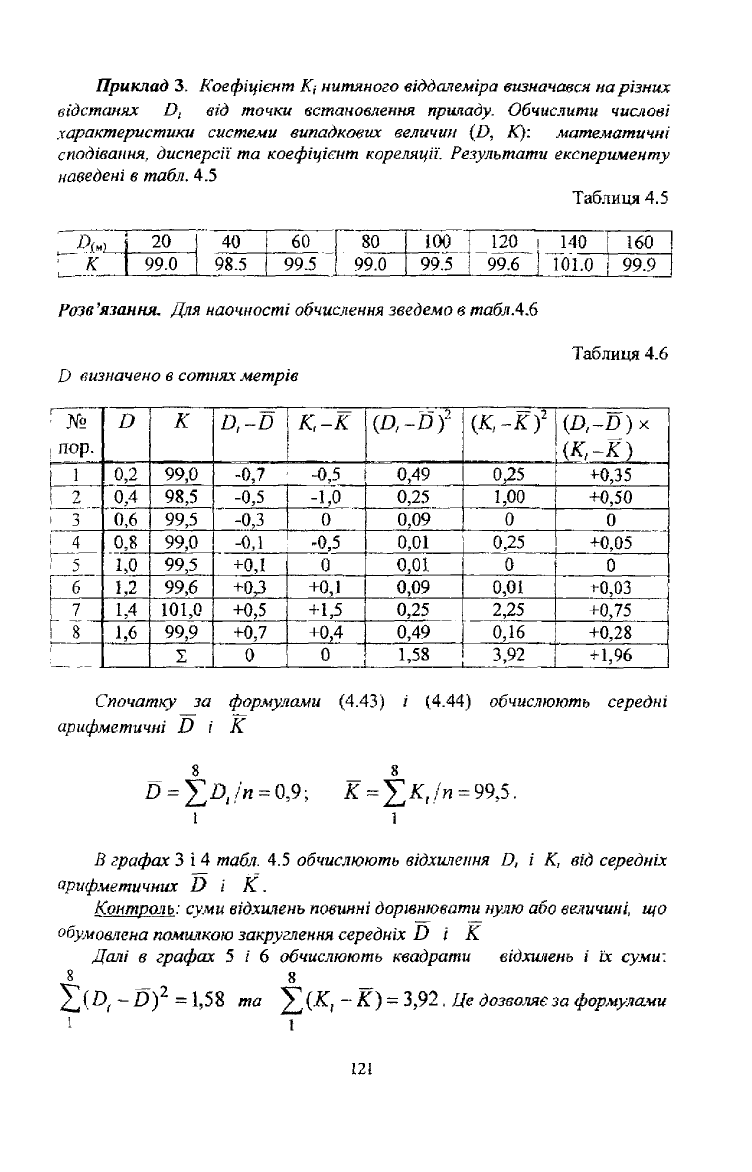
Приклад 3. Коефіцієнт КІ нитяного віддалеміра визначався на різних
відстанях Д від точки встановлення приладу. Обчислити числові
характеристики системи випадкових величин (О, К): математичні
сподівання, дисперсії та коефіцієнт кореляції. Результати експерименту
наведені в табл. 4.5
Таблиця 4.5
Ам
К
Розв'язання. Для наочності обчислення зведемо в таблА.6
Таблиця 4.6
О визначено в сотнях метрів
№
А К
Д-А
К,-К
(о,-пу (К,-ку
(А -А)х
пор.
(К,-К)
1
0,2 99,0
-0,7
-0,5 0,49
0,25
+0,35
2
0,4
98,5
-0,5
-1,0 0,25 1,00 +0,50
3 0,6
99,5
-0,3
0 0,09 0
0
4 0,8
99,0 -0.1 -0,5 0,01
0,25
+0,05
5
1,0
99,5
+0,1 0 0,01
0
0
6 12 99,6
+0,1
0,09
0,01
+0,03
7
1,4
101,0
+0,5
+ 1,5
0,25
2,25
+0,75
8
1,6 99,9
+0,7 +0,4
0,49
0,16
+0,28
2
0
0
1,58
3,92
Н
+1,96
Спочатку за формулами (4.43) і (4.44) обчислюють середні
арифметичні О і К
_ 8 _ 8
£>=]ГД/
И
= 0,9; К=%К,/п = 99,5.
1 з
В графах 3 і 4 табл. 4.5 обчислюють відхилення Д і К, від середніх
арифметичних А і К.
Контроль: суми відхилень повинні дорівнювати нулю або величині, що
обумовлена помилкою закруглення середніх А і К
Далі в графах 5 і 6 обчислюють квадрати відхилень і їх суми:
8 _ 8
£{Д -О)
2
= 1,58 та Е (К, - К )- 3,92 , Це дозволяє за формулами
1 1
20
99.0
40_
98.5
_60_
99.5
80_
99.0
_іро_
99.5
120
140
99.6 101.0
160
99.9
121
