Войтенко C.П. Математична обробка геодезичних вимірів. Теорія похибок вимірів

Подождите немного. Документ загружается.

3) відхилення випадкових величин від своїх математичних сподіві

не перевищує досить малої величини в порівнянні з відхилення

сумарної величини, тобто X; - М

Хі

< А.

Граничний закон розподілу для суми визначиться за формулою

1-І

Тоді, згідно з теоремою А.М.Ляпунова: Якщо випадкк

величини Х

Хі,...,Х

взаємно незалежні, мають один im

же закон розподілу з математичним сподіванням М

дисперсією D

при необмеженому збільшенні їх числа, зак

розподілу величин У (формула 3.69) необмежено наближаєте

до нормального. \

В гой же час, випадкові величини Х\, Хі, ,.., Х„ можуть м^

довільний розподіл імовірностей. Згідно з теоремою Муавра-Лалла

якщо всі випадкові величини X, однаково розподілені, дискрета

приймають тільки два можливих значення 0 чи і, то це передба

окремий випадок центральної граничної теореми.

Теорема Муавра-Лапласа описус поведінку біноміального розпод

при великих значеннях п. При цьому обчислення ймовірності попадай

випадкової величини Y в інтервал (0(, ß), що визначається за формуло)

Р(а < Т < ß) = £C„V"V, (З.

a<£<ß

може викопуватися за формулою

Р(а < У < ß) = ~

де q= 1 —р, р

—

ймовірність появи події в кожному із досліджень*

Збіжність закону розподілу випадкової величини Y до нормаль«

забезпечується за умови

І]м[

Хі

-М

lim _»=J _»о.

л-»<» СТ^ )

Розробку і доведення центральної граничної теореми викогі

П.Лаплас та А.М.Ляпунов. Великий внесок зробили П.Л.Чсбиі|

А.А.Марков, С.Н.Бернштейн, А.Я.Хинчип, А.1І.Колмогоров, Б.В.Гнедві

та інші.

а ~пр

Jlnpq І І Jbwq

(

102

Запитання д ля самоперевірки

1 Що називають системою випадкових величин?

2 Дайте визначення функції розподілу системи двох випадкових величин і

покажіть їх властивості

3 Як визначити ймовірність попадання випадкової точки в задану область'

4 Дайте визначення щільності розподілу системи випадкових величин та

назвіть її властивості

5 Які випадкові величини називають залежними та незалежними

6 Назвіть види залежностей між випадковими величинами

7 Приведіть функцію та графік щільності нормального розподілу двох

випадкових величин

8 Які числові характеристики двомірної випадкової величини''

9 Що називається кореляційним моментом та коефіцієнтом кореляції?

10 Приведіть формули кореляційного моменту та коефіцієнта кореляції для

системи двох дискретних випадкових величин

11 Які випадкові величини називають некорельованими?

12 Чи витікає із некорельованосп випадкових величин їх незалежність і

навпаки?

13 Що називають функщєю розподілу системи л-иипадкояих величин

14 Як визначається щільність розподілу системи «-випадкових величин''

15 За допомогою яких числових характеристик характеризують систему п-

випадкових величин?

16 Що називають кореляційною матрицею системи Я-випадкових величин'

17 Яка матриця називається нормованою кореляційною матрицею?

18 При яких умовах виникає діагональна матриця''

19 Що можна сказати про закон розподілу функції випадкових величин''

20 Як визначається математичне сподівання функції випадкових величин?

21 Чому дорівнює математичне сподівання суми та добутку випадкових

величин

22 Як визначається дисперсія функції випадкових величин'

23 Приведіть формулу для дисперсії функції некорельованих випадкових

величин

24 Запишіть систему декількох функцій системи випадкових величин

25 Запишіть у загальному вигляді математичне сподівання системи

декількох функцій системи випадкових величин

26 Напишить формулу кореляційної матриці функцій випадкових величин

27 Як визначити коефіцієнти матриць А і К

28 Яка сутність закону великих чисел''

29 Сформулюйте теорему Чебишова.

30 Які обмеження накладаються на випадкові величини в теоремі

Чебишова''

31 Яка сутність центральної граничної теореми Ляпупова?

32 При яких умовах виникає нормальний закон розподілу випадкових

величин''

103

ГЛАВА II. ЕЛЕМЕНТИ МАТЕМАТИЧНОЇ СТАТИСТИКИ

РОЗДІЛ 4. СТАТИСТИЧНА ОЦІНКА ПАРАМЕТРІВ РОЗПОДІЛУ

§ 1. Основні поняття і задачі математичної статистики.

Генеральна сукупність та вибірка

Математична статистика - дисципліна, яка займаєтьсщ

регістрацією, збором, описом і аналізом експериментальнщ

даних з метою вивчення закономірностей масових випадковщ

явищ. ,

Таким чином, всі задачі математичної статистики зводяться до

визначення методів обробки результатів експериментальних досліджені

(спостережень) масових випадкових явищ. <

Найбільш типовими задачами математичної статистики є: <>

1. Оцінка невідомої функції розподілу за результатами вимірів;

Якщо за результатами досліджень випадкової величини X одержана

значення Хі, х

, ..., х„ то необхідно приблизно оцінити невідому

функцію розподілу F(x). <

2. Оцінка точності невідомих параметрів розподілу. При вирішена!

цього питання обчислюють параметри функції розподілу випадково)

величини на основі отриманих результатів експерименту і оцінюючі

їх значення.

3. Статистична перевірка гіпотез. Якщо за результатам*

експерименту визначено функцію розподілу F(x) випадково^

величини X, то вирішується питання: чи дійсно випадкова величин^

X мас розподіл F(x) ?

При дослідженнях випадкових явищ виконують досить велику

кількість випробувань (експериментів) - N.

Генеральна сукупність - це сукупність значень результатів

досліджень (вимірів). Досить часто мають на увазі, що число N може

бути нескінченним. '

Проте практично виконати нескінченну кількість дослідів (вимірів^

або обстежити нескінченну кількість виробів неможливо, і економічно

невигідно. В цьому випадку із всієї генеральної сукупності відбираю™

обмежене число результатів експерименту. 1

Вибірковою сукупністю або просто вибіркою називаютц

сукупність випадково вибраних результатів чи об 'єктів.

104

Проте вибірка може як досить точно характеризувати досліджуване

випадкове явище, так і ні.

Представницькою або презентабельною вибірковою

називають об'єм вибірки п із генеральної сукупності

Ы,

який

дозволяє повною мірою визначити характеристики генеральної

сукупності, Інформація буде більш імовірною, коли результати

досліджень, що складають вибірку, будуть незалежними.

§ 2. Розподіл статистичних рядів

Практично, до початку досліджень випадкового явища, заздалегідь

невідомо, якому закону розподілу будуть підпорядковуватися результати

експерименту. Для його визначення над випадковою величиною X

виконують низку незалежних експериментів (вимірів). Результати вимірів

Ху ..., х„ і їх номер можна подати у вигляді статистичної таблиці 4.1

Таблиця 4.1

І 1 2 3

4 і

.. ! „

ХІ Х7 Хз

.. |

Статистична таблиця є початковою формою запису статистичного

матеріалу, який може оброблятися різними методами.

Однак при великій кількості експериментів (вимірів) їх результати

практично неможливо показати в статистичній таблиці. Тоді результати

спостережень розділяють на групи. Кожна група містить деяку кількість

(частоту) результатів, що належать визначеному інтервалу. Довжина

інтервалу розраховується за формулою Г.А.Стерджеса

І -

гщ.

.Т

*тіп

(4 п

3.21

де п - кількість результатів спостережень.

Можна задати число інтервалів к. Тоді довжину інтервалу визначають

за формулою

—

*тах ~ *тііі ^ 2)

Значення інтервалу / заокруглюють до зручного цілого значення так,

Щоб число їх було в межах 6 < к < 24.

105

Потім визначають граничні значення інтервалів за формулами

для

-ої групи х" = х

; ^ = х" + /;

для 2-ої групи х" = х*; х\ - х

+ І;

(4.3)

для к-ої групи х"

= х*_

; = + / = х

тах

·-

п к і

де х, ,х

(

- відповідаю початкове та кінцеве значення абсциси У

(результатів вимірів).

Для кожної групи підраховують частоту результатів V,. як

п • к • —

попадають в граничні значення х

і х

(

і статистичну ймовірність зі

формулою

Р, = — , (4-4)

причому Уі + у

+ ...+v

= п; р

+ р

+... + р^ -

1 •

За допомогою статистичної таблиці або статистичної сукупності:

можна побудувати статистичну функцію розподілу випадкової величині

х. !

Статистичною функцією розподілу випадкової величини ^

називають закон, за яким змінюється частота події X < х |

даному статистичному матеріалі, тобто ч

¥(х) = р{Х<х). (4.5)

Як бачимо, частота V,- практично пропорційно співвідноситься

імовірністю р, попадання випадкової величини X в кожну І-у груп;

визначену на основі статистичного матеріалу. Годі значення статистичні

функції розподілу згідно з формулою (4.5) обчислюються за формулою і

_ _ _ _ * '

Крім того, можна обчислити статистичну щільність розподілу д4

кожної групи за формулою "·•

Рі(х)

Ф,(*) =

Обчислені дані використовують для побудови графічного зображенії

статистичної функції. Дня цього по осі абсцис відкладають граничя

значення груп х", х?. Якщо по осі ординат відкласти значення частої

V, і отримані точки з'єднати ламаною лінією, то отримаємо поліпи

.1*

106

частот (рис. 4.1). При відкладенні значень отримують сходинковий

графік (рис.4.2), а при ф,(я)-гістограму (рис.4.3).

Приклад. Припустимо, що отримана статистична сукупність 100

похибок вимірів довжини лінії за допомогою електронного віддалеміра.

Розв'язання. За допомогою формул (4.1) - (4.7) зроблені необхідні

обчислення і занесені в табл. 4.2.

Таблиця 4.2

Граничні

значення

№ групи

Граничні

значення

Soc,

від

до (мм)

-20

-15

-10

-5

2 8 17 24

ІЗ

100

0,02 0,08 0,17 0,24

0,26 0,13

0,06

0,04

1,0

ЗД

0,02

0,10

0,27

0,51

0,77

0,90

0,96 1,00

0,004

0,016

0,034

0,048 0,052

0,026

0,012

0,008

Примітка /

—

5; k

—

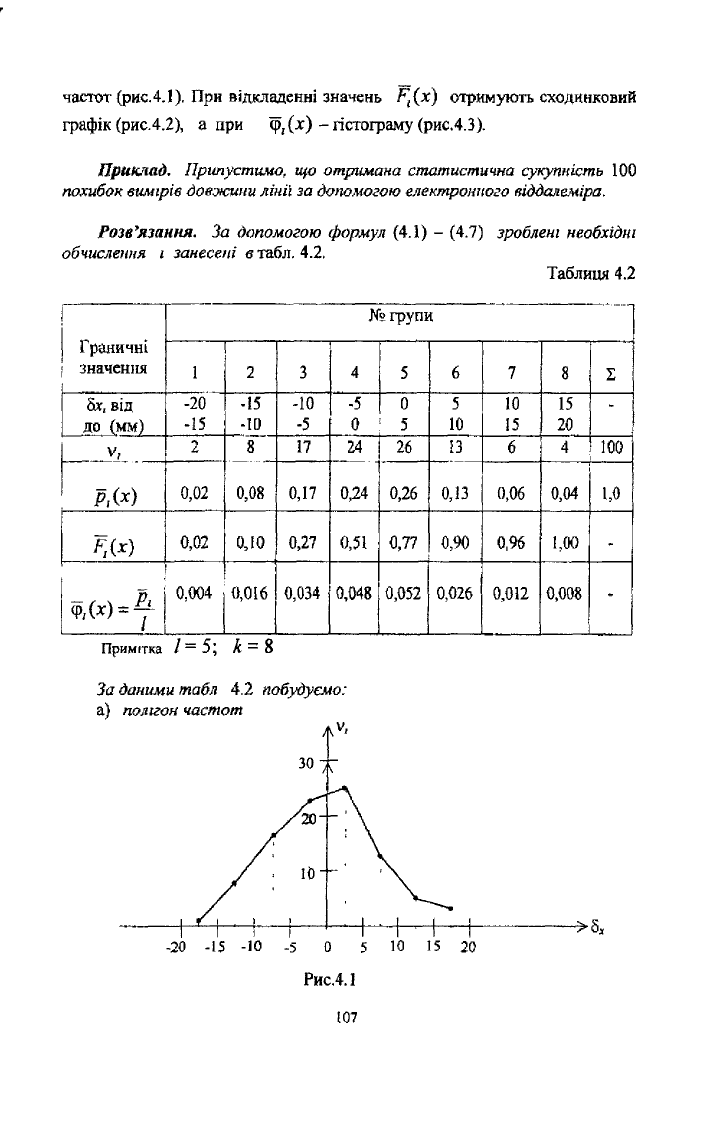
За даними табл 4.2 побудуємо:

Рис.4.1

107

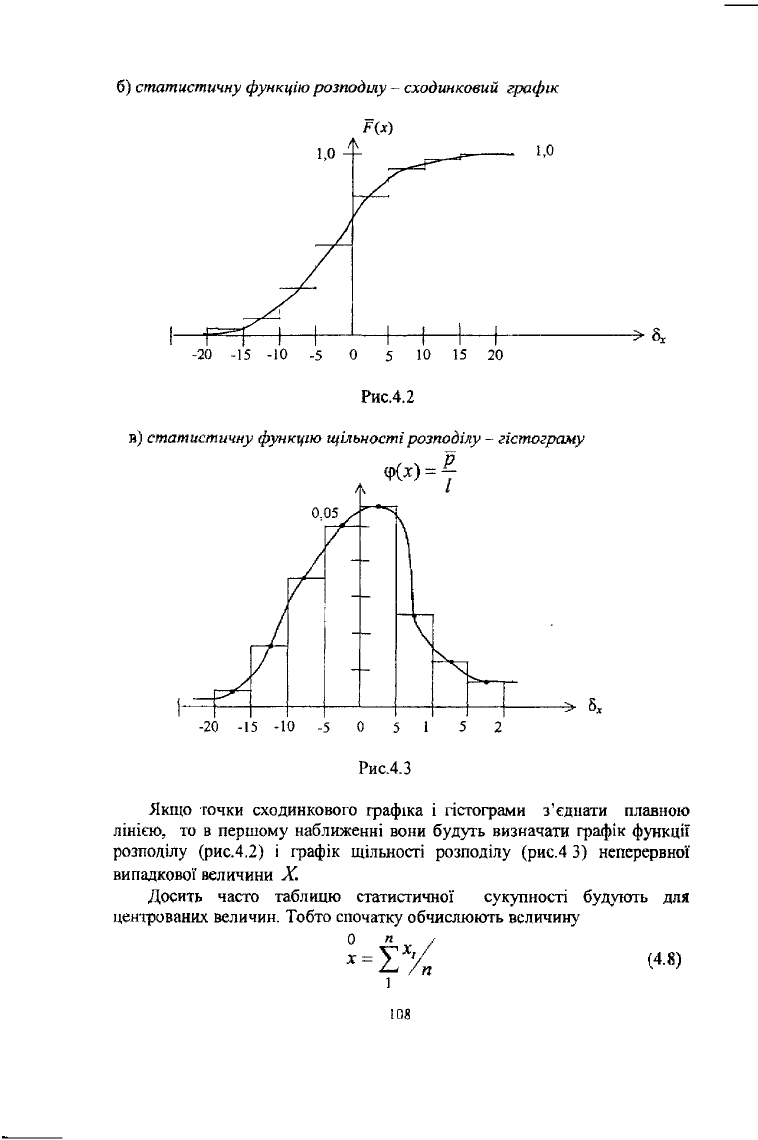
б) статистичну функцію розподілу - сходинковий графік

¥(х)

Рис.4.2

в) статистичну функцію щільності розподілу - гістограму

Рис.4.3

Якщо точки сходиикового графіка і гістограми з'єднати плавною

лінією, то в першому наближенні вони будуть визначати графік функції

розподілу (рис.4.2) і графік щільності розподілу (рис.4 3) неперервної

випадкової величини X.

Досить часто таблицю статистичної сукупності будують для

центрованих величин. Тобто спочатку обчислюють величину

0 П ,

= Т

'/п (

108

, відхилення

5х, =х

{

-х (49)

Подальші розрахунки здійснюють за формулами (4 1) - (4 7), де

замість величин х

тах

, *

шш

беруть відхилення 5,

ГШ1

і х",х^ -

Відповідно і на графіках значення абсциси х заміняють

відхиленнями 5

Слід зазначити, що в прикладі статистична сукупність так і

розрахована в табл 4 2 Тобто за величину X взято відхилення результатів

вимірів лиш від середньої центрованої величини, а не довжини ліній

§ 3. Оцінювання параметрів закону розподілу

Відомо, що випадкова величина X характеризується законом

розподілу, що має деякі невідомі параметри а{а\. а

, , а*)

(§ 4 з розд 2). Якщо в результаті виконаного експерименту нами отримано

статистичний ряд Х

, , Х

, то очевидно можна знайти надійну оцінку

параметра а.

Припустимо, що на основі обробки статистичного ряду отримано

параметр а, який буде оцінкою невідомого параметра а Разом з тим,

вш буде функцією від випадкових величин Х{, Х

, , Х

, тобто

а=а (Х

, , Х„) (4 10)

Таким чином і обчислений параметр а буде випадковою

величиною, закон розподілу якого залежить від закону розподілу

випадкової величиниX і від числа експериментів п При цьому оцінка а

б\де мати практичну цінність, якщо володіє властивостями

1 Незміщеностг При цьому повинна виконуватися умова

=М[а{Хі,Х

, ,Х

)]=а, (411)

Де а - істинне значення параметра.

2 Обгрунтованості Тобто за ймовірністю вона зводиться до

оцінюваного параметра при нескінченному збільшенні кількості дослідів,

тобто

ІтР[\3(Х

, , Х„)-а\<ї] = 1, (4 12)

«->00

;;е

Е, -

як

завгодно мале позитивне число

109

Для цього потрібно, щоб дисперсія оцінки а наближалась до нуля при

п —»ос, тобто

Ііш Ща(Х

, ..., Х

)]

3. Ефективності. Цс означає, що дисперсія ОЦІНКИ а повинна буп

мінімальною, тобто

При цьому буде мінімальна ймовірність появи грубої помилки прі

визначенні наближеного значення невідомого параметра

Таким чином при розробці методів обробки статистичних даних ллі

визначення оцінок наближених значень невідомих параметрів требі

виходити з їх властивостей. Оцінки параметрів закону розподілу, ще

відповідають всім трьом властивостям називають доброякісними.

Практично розроблено три способи визначення оцінок: мето;

моментів; метод максимальної правдоподібності (ММП); метол

найменших квадратів (МНК)

В методі моментів значення теоретичних моментів замінякхи

значеннями емпіричних моментів, які обчислюють за результатам

статистичних рядів чи статистичної сукупності (§ 4; розд.4).

В методі максимальної правдоподібності (ММП), розробленої^

Р. Фішером розглядають значення випадкових величин X] ,х

, .., х„,

отримані при проведенні дослідів і використовують їх для визначенні

невідомого параметра а Якщо щільність розподілу ер (х, а) залежить віл

параметра а, то в ММП задаються правдоподібною функцією, виходячи з

того, що всі х, незалежні

І(х

..·, х„, а) = ф (х

а) ф (х

, а)... ф (х„, а). (4.14)

Сутність ММП полягає в тому, що за якісну оцінку параметра 4

беруть таке значення аргументу, яке приводить функцію 1. до максимуму!

Рівняння (4.14) розв'язуюсь за умови

При цьому вибирають таке визначення а, яке зводить функцію

максимуму. Для спрощення функцію правдоподібності замії

логарифмом, тоді

ШІП ·

(4.із;

8\аІ 1 ді

= 0

<4.М|

да Ь 5а

по

Якщо закон розподілу має два параметри а\ і а

, то оцінки їх

визначають із сумісного розв'язання двох рівнянь

ділі

ділі „

—— =0 і -г—= 0 (4 17)

Ш] да

Приклад 1. При експериментальних випробуваннях точності

розробленого приладу отримана вибірка із генеральної сукупності

X: х

, х

Результати вимірів х, незалежні між собою Попередні

розрахунки показали, що статистична функція (гістограма) має вигляд

щільності нормального розподілу Необхідно знайти оцінку для невідомого

параметра а = М

, що відображає ймовірне значення шуканої величини

Розв'язання. Так як результати експерименту підпорядковуються

нормальному закону розподілу, то висунемо умову що щільність розподілу

кожної із величин ф(лг„ а) залежить від параметра а. Це означає що для

кожної величини функції правдоподібності буде

(х,

-а)

л/ 2тто

Тоді функція правдоподібності для всієї вибірки буде

Ь(х

х2, ,х

,а)=І

. \

Візьмемо логарифм, тоді

ІпІ = Щ-ІТліУ" - піпа - ^

2ст

1а допомогою формули (4 16) отримаємо

2 £(х,-а)

і л

да 2 от

сг

При цьому необхідно щоб сг

Ф 0, тоді

п п

- а) = 0, або ^ лс, - па = 0

і=1 і=1

;=1

111