Войтенко C.П. Математична обробка геодезичних вимірів. Теорія похибок вимірів

Подождите немного. Документ загружается.

Функція розподілу має такі властивості:

1. Якщо один із аргументів наближається до плюс нескінченності, т

функція розподілу системи наближається до функції розподілу випадков(

величини другого аргументу, тобто

F(x, +02)

—

F і(х);

у) = Р

(у).

2. При наближенні обох аргументів до плюс нескінченності функи

розподілу F (х,у) наближається до одиниці:

lim /

(х,у) = 1, або F(+°о, +оо)=1,

у-> <ю

3. При наближенні одного чи обох аргументів до мін;

нескінченності функція розподілу наближається до нуля:

lim F(x,y)= lim F(x,y)= lim F(x,y) = 0,

x—> - « i—> - 00 y—> - П)

y-¥ -

або F (- 00, y) = F(x. - 00) = F (- 00, - 00) = 0.

4. Функція розподілу (F (x, у) є зростаючою функцією з кожне

аргументу:

F(x

,y) > F{x\, у), якщо х

>хі;

F (х, у

) > F (х, у

{

), якщо у2 > у,.

5. Ймовірність попадання випадкової точки (х,

в будь-як

прямокутник зі сторонами, паралельними координатним осі

обчислюється за формулою

р{х

<Х<х

, y

{

<Y<y

) = F(x2,y

) - F(x

)

- F(x

,y]) +F(xi,ji). (3.

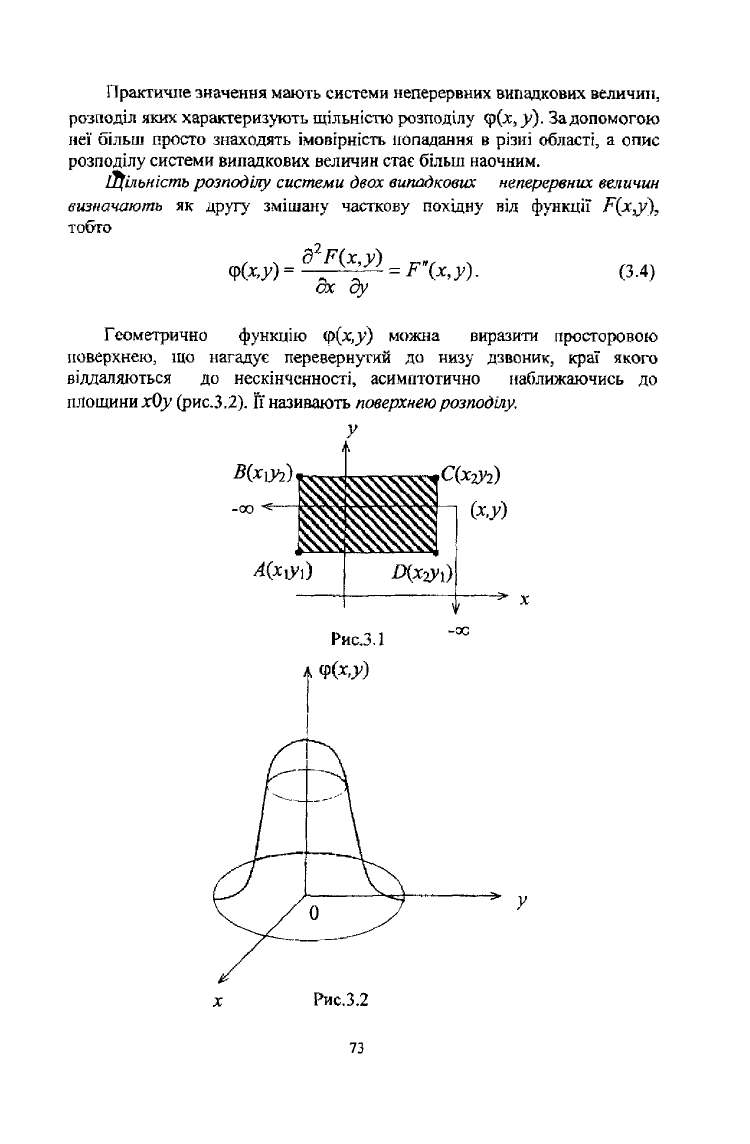
Це легко з'ясувати геометрично, якщо уявити положен

прямокутника з координатами вершин А( jcj, _уі), В(х\,у

), С( х

і D( x2,y\) нарис.3.1 і геометричними значеннями функцій F{ x

..., в формулі (3.3).

Практичне значення мають системи неперервних випадкових величин,

розподіл яких характеризують щільністю розподілу ф(х, у). За допомогою

неї більш просто знаходять імовірність попадання в різні області, а опис

розподілу системи випадкових величин стає більш наочним.

Щільність розподілу системи двох випадкових неперервних величин

визначають як друг}·· змішану часткову похідну від функції

тобто

= (3.4)

дх ду

Геометрично функцію ір(х,у) можна виразити просторовою

поверхнею, що нагадує перевернутий до низу дзвоник, краї якого

віддаляються до нескінченності, асимптотично наближаючись до

площини хОу (рис.3.2). Гі називають поверхнею розподілу.

В(х їй)

Рис.3.1

л Ф(Х>0

Рис.3.2

Функція розподілу Р(х,у) визначається за формулою

* у

Пху)

| | Ф(х,у)сіхсіу. (3.5)

-00 —00

Щільність розподілу системи двох випадкових величин м<

властивості:

1. Щільністю розподілу є функція

Ф,У) > 0-

2. Подвійний інтеграл з нескінченними межами від функ

щільності розподілу дорівнює одиниці:

+оО

+со

І |

ц>(х,у) сіхсіу =

-СЗО

—00

Геометрично це свідчить про те, що об'єм тіла, відмежоване

поверхнею розподілу і площиною хОу, дорівнює одиниці.

Щільності розподілу величин х та у, що входять в систеї

визначають за формулами:

+00

ФіО) = | Ф,у) Лу;

Фг0)= І ф(х,у)(іх

Тобто, для визначення щільності розподілу однієї із сястя

випадкових величин, треба проінтегрувати в необмежених ми*

щільність розподілу системи ф(х,У) за аргументом другої випадкої

величини.

Якщо відомі щільності розподілу окремих випадкових вели^

системи і випадкові величини х та у незалежні між собою, то моя!

визначити закон їх сумісного розподілу за формулою

ф(х,у) =фі(х) · ф

(у).

Подібно умовній імовірності Р ^ для подій визначаКІ

умовні щільності розподілу:

1) ф - щільність розподілу у при умові, що випадкова

величина X прийняла значення х;

ф - щільність розподілу х при умові, що випадкова

величина У прийняла значення у.

Закон її сумісного розподілу визначають за формулою

або у(х,у) = ф

(»ф

ф (х,у) = фіООф

Поняття залежності та незалежності випадкових величин має велике

значення в теорії ймовірностей та при математичній обробці результатів

вимірів.

Випадкова величина X буде незалежною від випадкової величини У,

якщо закон розподілу величини X не залежить від прийнятого значення

величини 7, тобто

Випадкові величини X і У незалежні, якшо щільність сумісного

розподілу ф(Х>') можна визначити у вигляді добутку двох множників,

кожен із яких утримує тільки величини х та у, тобто

Додамо, що при розкладанні, функції <х(х), (З(^) з точністю до

постійної множників збігаються з щільностями розподілу фі(х) і ф2(у).

і навпаки, для випадкової величини У маємо

Якщо вони взаємно залежні між собою, то

Ф,У) = а(х)-рО)-

Між випадковими величинами виникає функціональна а4

стохастична (ймовірна) залежність.

Функціональною залежністю між випадковий

величинами X і У називають таку залежність, коли кожноі

значенню X відповідає точне значення У.

2 І

Наприклад, у ~ X , 5

—

а-Ь І т.д. І

Стохастичною (ймовірною) залежністю м^

випадковими величинами Хі У називають таку залежність, щ

якій кожному значенню х можна вказати розподіл величини

яке змінюється при зміні х.

Така залежність в практичній діяльності зустрічається досить часі

Наприклад, зріст та вага людини, висота і товщина дерева в лісі, величні

деформації інженерних споруд, час їх експлуатації і т.д.

Тобто у випадку ймовірної залежності на кожне точне знач·

аргументу х можна вказати значення випадкової величини у з певі

мірою ймовірності (Ру)-

Система двох випадкових величин може підкорятися різним закої

розподілу. Проте в практиці геодезичних вимірювань найбіш

розповсюдження має нормальний закон розподілу.

Якщо випадкові величини X і У мають нормальний розпод

незалежні між собою, то щільності розподілу кожної із них будуть:

К*-м

)

1 2

9і(*)

Г=Г

' і

ч2%

і (.У-Му)

! Л

у/2п

Згідно з формулою (2.69) щільність розподілу системи (X, У), я*

випадкові величиниXта У незалежні, отримаємо у вигляді

ф,У) =

-і

(х~М

)

(.У-Му)

}

2к

(3.:

Якщо центр системи (х,_у) знаходиться на початку системи координат

хОу, тобто М

= М

= 0, то

Ф(*.;и) =

^ аі )

(3.8)

Поверхня щільності нормального розподілу системи (х,у) має

опуклий вигляд (горб), показаний нарис.3.2.

Ймовірність попадання випадкової точки в прямокутник із сторонами

паралельними осям координат, в межі з координатами х^хі і }і-}'2

(рис.3.1) визначається за формулою

2 У2

Р(х

{

<Х<х

, < У < у

) = { І Фу)

СІХ

ф. (3.9)

І У\

При нормальному розподілі системи двох випадкових величин

отримаємо

,1 - М

-ф

—

ф —

-ф

(у

-М. ^

V У

У\ ~

> .

(3.10)

Приклад 1. Щільність розподілу системи двох випадкових величин

(X, V)

визначається за формулою

Ф>У)

, Г^ТІ 2·

+ х+х^у +

Знайти: а) значення а: б) функцію розподілу; в) визначити

залежність випадкових величин X і К

Розв'язання, а) Згідно з 2-ою властивістю щільності розподілу

маємо

+ 00 ОО 00

\ І

1 +

+ х

+ 1'

-00 ^

(іхйу = а І І

сіхсіу

+ + Г)

г сіх г ау

+ ж

І 1+ у

•ат^у

= оп =1.

Тоді

а =

.2 '

б) з а формулою (2.68) отримаємо

X У

= ~ 1 !

сШу (І

IV1 1

и 2 д 7і 2

в) при відомому значенні а

—

— функція щільності дорівнює

Ф.У) =

Ц—^ ^ •

(1 + х

+х

+у

)

її можна розкласти на множники, тобто

Ф,у)

7Г

(1 + х

)(1 + /)'

Це свідчить про те, що випадкові величини X і У незалежні. То

фі

(

;

71(1

+ Х )

Ф:0') =

·,-.

<1 + /)

Приклад 2. Визначити ймовірність попадання точки в прямок)

з координатами: х,

™

1; х

• 3; у і ~ 2; у

- 4, ям/у о щільність розі

системи випадкових величин

(.X, У)

підпорядковується нормальному з

з центром розсіювання є точці х = 2, у

—

3 і стандартом о, =

0,5.

Розв'язання. Згідно з формулою (З.Щмаємо

Р(х

< X < х

, у

< У < у

)

-Ф

У2-У

V ^

-Ф

Уі -у

°у ^ J

= і[

(р

(2)-ф(-2)] [ф(2)-ф(-2) ].

За таблицею функцій Лапласа (дод.1) знаходимо <р(2) = 0,95;

ф(-2) = -0,95.

Тоді Р = -(0,95 + 0,95) (0,95 + 0,95) = 0,9.

§ 3. Числові характеристики системи двох випадкових

величин. Кореляційний момент, коефіцієнт кореляції і

рівняння регресії

Найбільш повними ймовірними характеристиками системи двох

випадкових величин є закон розподілу. Однак в практичній діяльності не

завжди є можливість визначити його. Тому при дослідженнях систему

двох випадкових величин характеризують їх числовими характеристиками:

початковими та центральними моментами.

Початковим моментом <хпорядку 5, ц системи (X, У)

називається математичне сподівання від добутки Х^' на У,

тобто

ЗЧ

=М[Х

1 (3.11)

Для системи дискретних випадкових величин

Кц^хЇУЇРх.У, > (3.12)

де Рхуі = Р(Х = х,; У ~ у,) - ймовірність того, що система (х,у) прийме

значення (х^і), а додавання розповсюджується по всіх можливих

значеннях випадкових величин X і У.

Для системи неперервних випадкових величин

00 оо

1 \х*У

Ф.У)<іхсїу, (3.13)

—оо

— со

де ф(х,>') - щільність розподілу системи двох випадкових величин X та

В практичній діяльності найчастіше використовують початкові

моменти першого порядку при 5=1,

= 0 і $

0, д

—

І згідно з

Формулами (3.11) і (2.15):

=М[Х

[

У°] = М[Х] = М

·, (3.14)

=М[Х°У^] = М{У) = М

. (3.15)

Як видно із формул (3.14) і (3.15) початковими моментами першої

порядку будуть математичні сподівання випадкових величин X і У. Воі

визначають координати точки, яку називають центром розсіювані

системи (X, У) на площині.

Центральним моментом \і

порядку $$ системи (X, ]

називається математичне сподівання добутку центровані

величин (X- М

) і (У- М

) відповідно в 5-му і д-му степенях,

\і

=М[(X- М^ (У

•

)

]. (З.І63

Для системи дискретних і неперервних величин отримаємо:

Щ = X (*, - М

У(У, - Му? Р

хуі

; (3.17)

00 СС

^ = I | (х- М

)

(у - М

)

ф,у) сіх ф. (3.18)

-00

—00

Практичне значення мають центральні моменти другого порядку пр

з = 2 і д = 0 таі = 0 і д

1120= М[(Х-М

)

(У-Му)°]=М[(Х-М

)

]= Б

; (3.19)

= М[(Х-М

)° (У-Му)

] - М

[(Г-Му)

}

= Иу. (3.20]

Як видно вони с дисперсіями випадкових величин X та У

характеризують розсіювання випадкової точки з координатами (х, у),

напрямку осей Ох і 0у.

При дослідженнях системи випадкових величин важливу роль мі

змішаний центральний момент першого порядку - Цп. Його називаю^

кореляційним моментом К

ху

або моментом зв 'язку і визначають і

формулою '

\а

= К

у = М[(Х-М

)(У~М

)}. (3.21]

Для системи дискретних та неперервних величин його визначаю^

за формулами і

= !>,"М

)(

Уі

-М

)Р;

іУі

, (3.23

і '

00 00

Кху = { \

(Х-М

)(у-

Му)у(х,у)ск<іу. (3.23

—

00 —оо

В § 2 цього розділу показано, що між випадковими величинами

X і У може виникати зв'язок. Кореляційний момент К^ і характеризує

сИ

лу або щільність зв'язку. Відомо, (якщо між випадковими величинами

[снує ймовірний зв'язок (залежність), то зі зміною випадкової величини X

змінюється закон розподілу випадкової величини У.,В той же час закон

розподілу задають кривою розподілу у Характер кривих може бути

різним, тому і відрізняють декілька типів імовірної залежності. Одним із

найбільш розповсюджених типів є кореляційна залежність, за якої

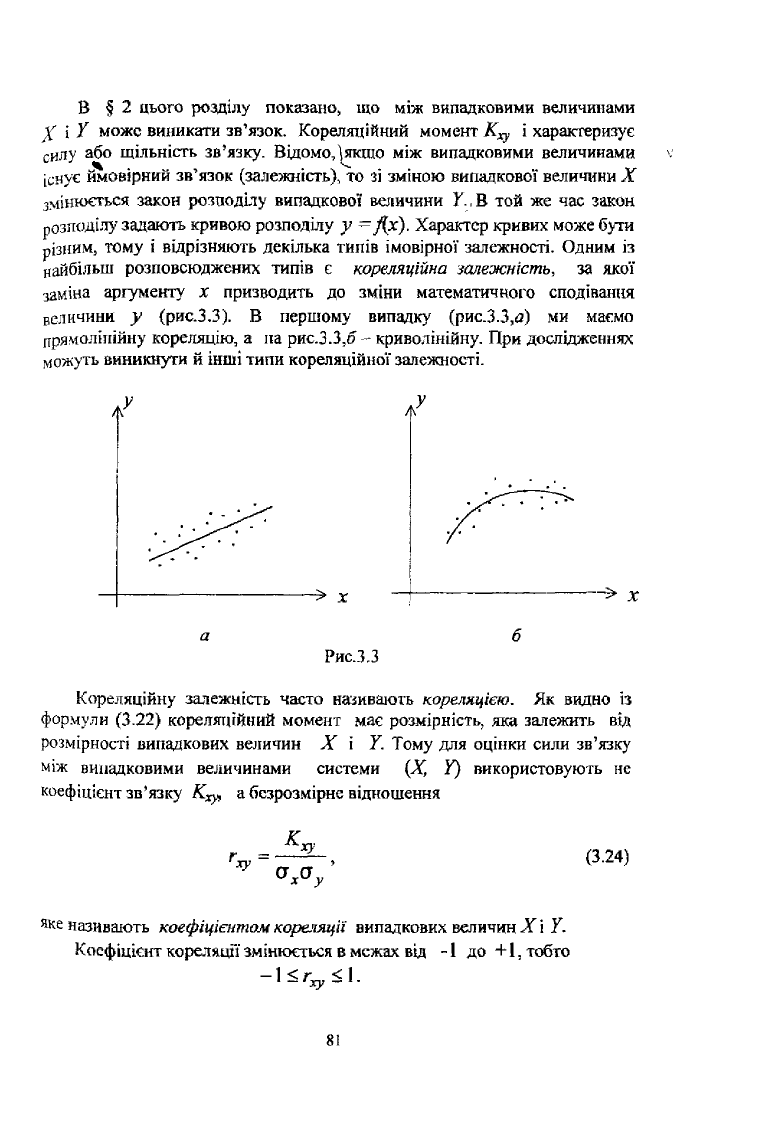
заміна аргументу х призводить до зміни математичного сподіванім

величини у (рис.3.3). В першому випадку (рис.3.3,а) ми маємо

прямолінійну кореляцію, а па рис.3.3,б - криволінійну. При дослідженнях

можуть виникнути й інші типи кореляційної залежності.

Рис.3.3

Кореляційну залежність часто називають кореляцією. Як видно із

формули (3.22) кореляційний момент має розмірність, яка залежить від

розмірності випадкових величин X і У. Тому для оцінки сили зв'язку

між випадковими величинами системи (X, У) використовують не

коефіцієнт зв'язку Кху, а безрозмірне відношення

ху =

ху

<*х°у

(3.24)

яке називають коефіцієнтом кореляції випадкових величин X

У.

Коефіцієнт кореляції змінюється в межах від -1 до +1, тобто

-1<г

—

ху

—