Войтенко C.П. Математична обробка геодезичних вимірів. Теорія похибок вимірів

Подождите немного. Документ загружается.

3 J ... | і

Р,

РЧ

Р 1 ... ! <fV

Математичне сподівання згідно з формулою (2,16) визначіться

сумою ряду

Мх

1 *р + 2 · qp + 3 -q

p + ... + і

•

іЛ

р + ...=

= р{ 1 + 2q + 3q

+ ...+iq'~

+ ...).

В дужках отримано результат диференціювання геометричної

прогресії

q + q

+ q

+ ...+q

+ ...=

-q

2 (1 '1

Отже 1 + 2q + 3q + ...+i q' + ... = =

——•.

(i-?)

P і

Тоді M

^-4r = —.

P P

2) Мода і медіана випадкової величини

Модою Мо дискретної випадкової величини називають таке

її значення, що має найбільшу ймовірність.

Практично, якщо маємо дискретний ряд розподілу, то знаходимо таке

k-e значення випадкової величини х, що має найбільшу величину

ймовірності Р

(к)-

Для неперервної випадкової величини модою буде таке її значення,

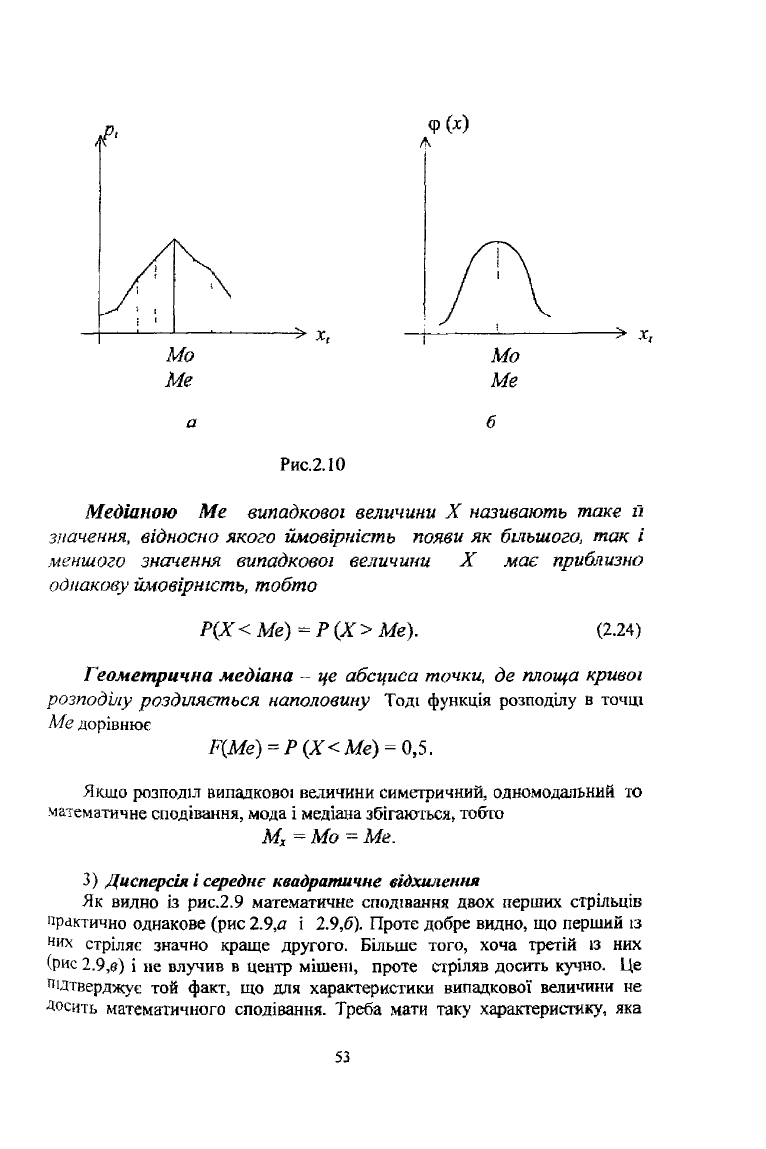
що має максимум щільності розподілу, тобто ср(Mo) = max. На рис.2.10,<з

і 2.10,6 показано моду для дискретної та неперервної випадкової

величини.

ЯКЩО многокутник розподілу або крива розподілу має два або

більше максимумів, то такий розподіл називають

двохмодальним чи багатомодальним.

В прикладі І § 3, розд.2 модою буде Xj, так як рз = 0,35 = max.

ФО)

> X.

+ X,

Мо

Ме

Мо

Ме

Рис.2.10

Медіаною Ме випадкової величини X називають таке її

значення, відносно якого ймовірність появи як більшого, так і

меншого значення випадкової величини X має приблизно

однакову ймовірність, тобто

Геометрична медіана - це абсциса точки, де площа кривої

розподілу розділяється наполовшу Тоді функція розподілу в точці

Ме дорівнює

Якщо розподіл випадкової величини симетричний, одномодальний то

математичне сподівання, мода і медіана збігаються, тобто

3) Дисперсія і середнє квадратичне відхилення

Як видно із рис.2.9 математичне сподівання двох перших стрільців

практично однакове (рис 2.9,а і 2.9,6). Проте добре видно, що перший із

них стріляє значно краще другого. Більше того, хоча третій із них

(рис 2.9,в) і не влучив в центр мішені, проте стріляв досить кучно. Це

підтверджує той факт, що для характеристики випадкової величини не

Досить математичного сподівання. Треба мати таку характеристику, яка

Р(Х<Ме) =Р(Х>Ме).

(2.24)

Г<\Ме) = Р(Х<Ме)-0,5.

= Мо = Ме.

відображає розсіювання випадкової величини. Такими основними

характеристиками є дисперсія та середнє квадратичне відхилення.

Очевидно, що величину розсіювання для кожної випадкової

величини від математичного сподівання можна обчислити, тобто

X =Х~М

Величину X називають центрованою випадковою величиною. Так як

імовірність появи центрованих випадкових величин X справа і зліва від

однакова, то її математичне сподівання дорівнює нулю і не може

характеризувати розсіювання її значень. Тому якістю міри розсіювання X

беруть математичне сподівання від квадрата відхилення випадкової

величини від її математичного сподівання і називають його дисперсією -

А,

Дисперсією випадкової величини с математичне сподівання

квадрата відхилення випадкової величини від її математичного

сподівання, тобто

= М[(Х-М

)

}. (2.25)

Для дискретної випадкової величини дисперсія матиме вигляд суми

=2>

-Л0

Л·. (2-26)

для неперервної це буде інтеграл

= |(х-М

)

ф(д:)£&. (2.27)

— 00

Дисперсія має розмірність квадрата розмірності випадкової величини,

що не зовсім зручно. Тому для характеристики міри розсіювання

випадкової величини приймають додатковий квадратичний корінь із

дисперсії. Цю характеристику називають середнім

квадратичним відхиленням або стандартом і позначають

символом а

х ~ • (2-28)

Стандарт має таку саму розмірність, як і випадкова величина X.

Дисперсія має такі властивості:

1. Дисперсія постійної величини дорівнює нулю

ДО = 0. (2.29)

2. Дисперсія добутку постійної величини на випадкову величину

дорівнює добутку квадрата постійної величини на дисперсію

випадкової величини

ЩСХ) = С

Якщо маємо декілька таких добутків, то

(2.30)

(2.31)

і=1 1=1

3. Дисперсія випадкової величини дорівнює математичному

сподіванню її квадрата мінус квадрат її математичного сподівання

ІХХ) М

. (2.32)

Прикладі. Визначити дисперсію виміру кута п'ятьма прийомами.

Ряд розподілу приведений в прикладі

розд.2

Розв'язання. В прикладі 1 § 3; розд.2 обчислене математичне

сподівання дорівнює М

= 3. Тоді за формулою (2.27) дисперсія виміру

кута буде

= ^{ХІ~М

)

Рі

= (-3)

0,01 + (-2)

0,08 + (-1)

0,23 +

і=1

+ О

· 0,35 + І

- 0,26 + 2

-0,07= 1,18.

Приклад 4. Випадкова величина X задана щільністю розподілу

0 при

Ф0с)

СОБ X при

•к п

2 2

Визначити дисперсію і середнє квадратичне відхилення випадкової

величини X.

Розв 'язання. За формулою (2.17) визначимо математичне сподівання

= | хсоз;к& =

ХБІПД:

я/

•'2

- |8ІпжЛ = 0.

-К/

Якщо М

—

0, то за формулою (2.27) знайдемо

= І х

со$хсіс - 2хсозд:

+ (* -2)зіпх

-8

Тоді середнє квадратичне відхилення, або стандарт буде

х = \\-"

-8

4). Моменти випадкової величини

Узагальненням основних числових характеристик випадкових

величин є моменти випадкової величини. Визначають початкові та

центральні моменти.

Початковим моментом к-го порядку випадкової величини

Xназивають математичне сподівання від величини Х

, тобто

(Х

=М[Х

]. (2.33) і

Для дискретної випадкової величини початковий момент буде

1=1

(2.34)

для неперервної

«і - І** <р(х) СІХ.

(2.35)

При порівняні формул (2.15) і (2.17) з формулами (2.34) і (2.35)

видно, що початковий момент першого порядку є математичне сподівапн^

випадкової величини, тобто (Хі = М

Центральним моментом к-го порядку випадкової

величини X називають математичне сподівання від величині

{Х-М

)

. і

Тоді

]ч

=м[{Х-м

)

для дискретної випадкової величини:

ч к ,

г=1

для неперервної величини:

+да

Ц*

= \(х - М

)

ф(х) сЬ.

(2.36)

(2.37)

(2.38)

Очевидно, що центральний момент першого порядку завжди буде

дорівнювати нулю. При порівнюванні формул (2.26), (2.27), (2.28) з

формулами (2.36), (2.37) і (2.38) видно, що центральним моментом

другого порядку є дисперсія випадкової величини X.

5) Асиметрія та ексцес.

Третій центральний момент (із служить характеристикою асиметрії

(скошеїіість) розподілу. Якщо = 0, то ми маємо симетричний

розподіл випадкової величини відносно математичного сподівання.

Асиметрія — це відношення третього центрального

моменту до середнього квадратичного відхилення в третьому

степені

с -Ні

*** - з -

(2.39)

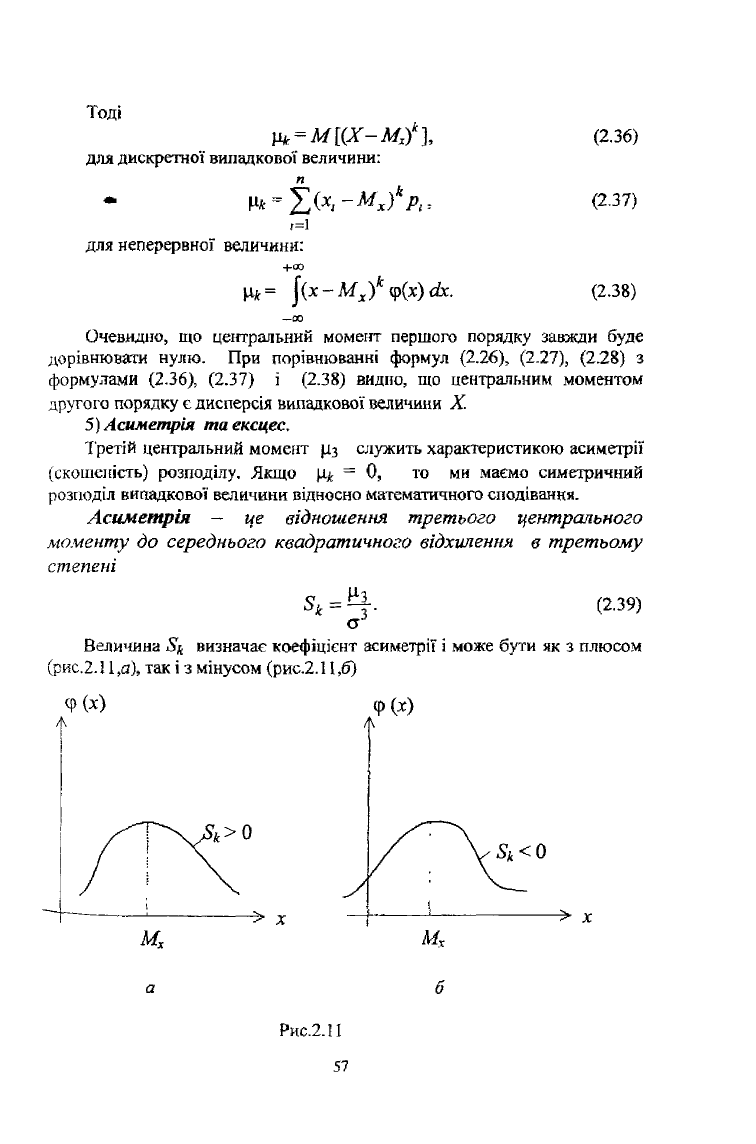
Величина визначає коефіцієнт асиметрії і може бути як з плюсом

(рис.2.1 і,а), гак і з мінусом (рис.2.11,6)

<р(х)

Ф 00

.У

Рис.2.11

Четвертий центральний момент 5X4 служить для обчислення ексцес}

характеристики

островерхого або плосковерхого розподілу

Ексцесом випадкової величини X називають величину, щ

описується залежністю

Якщо Ек = 0, то крива розподілу буде еталоном, з яким зрівнююі

інші закони розподілу Так при Е

> 0 крива буде більш гостроверхою,

при Еь< 0 - плосковерхою (рис 2 12)

Рис 2 12

Математичне сподівання, мода, медіана, дисперсія, середі

квадратичне відхилення, моменти, асиметрія і ексцес використовують Ді

характеристики випадкових величин при вирішенні великої кількос

практичних задач, коли закон розподілу або не потрібний, або його і

можна визначити Треба пам'ятати, що кожна із числових характерней

відображає ту чи іншу властивість закону розподілу

Центральні моменти можна виразити через початкові моменти

= а

- а? = Д ,

}і4 = - 4а]ОСз

6а

<х

На практиці іноді використовують так звані абсолютні початкові та

центральні у,у моменти, що визначаються залежностями:

=M[\x

|];

(2.42)

Неважко помітити, що абсолютні моменти парних порядків

збігаються зі звичайними моментами. Абсолютний центральний момент

першого порядку є середнє арифметичне відхилення.

§ 4. Нормальний закон розподілу випадкових величин

Нормальний закон розподілу випадкових величин має важливе

значення в теорії ймовірностей і найчастіше зустрічається на практиці.

Головна його властивість полягає в тому, що серед інших законів він є

граничним законом, до якого наближуються інші закони розподілу в

досить частих подібних типових умовах. Доведено, що більшість

випадкових величин, якому б закону розподілу не підкорялися, в сумі

великого числа додатних нівелюються, а сума Гх підкоряється закону

досить близькому до нормального закону. Це твердження відноситься і

до результатів геодезичних вимірів.

Неперервна випадкова величина має нормальний розподіл,

якщо щільність імовірності має рівняння

де е = 2,718..., 7t = 3,141..., М

- математичне сподівання, CT -

середнє квадратичне відхилення (стандарт). М

та <т називають

параметрами нормального закону розподілу. Якщо відомі значення М

о, то щільність імовірності повністю визначена

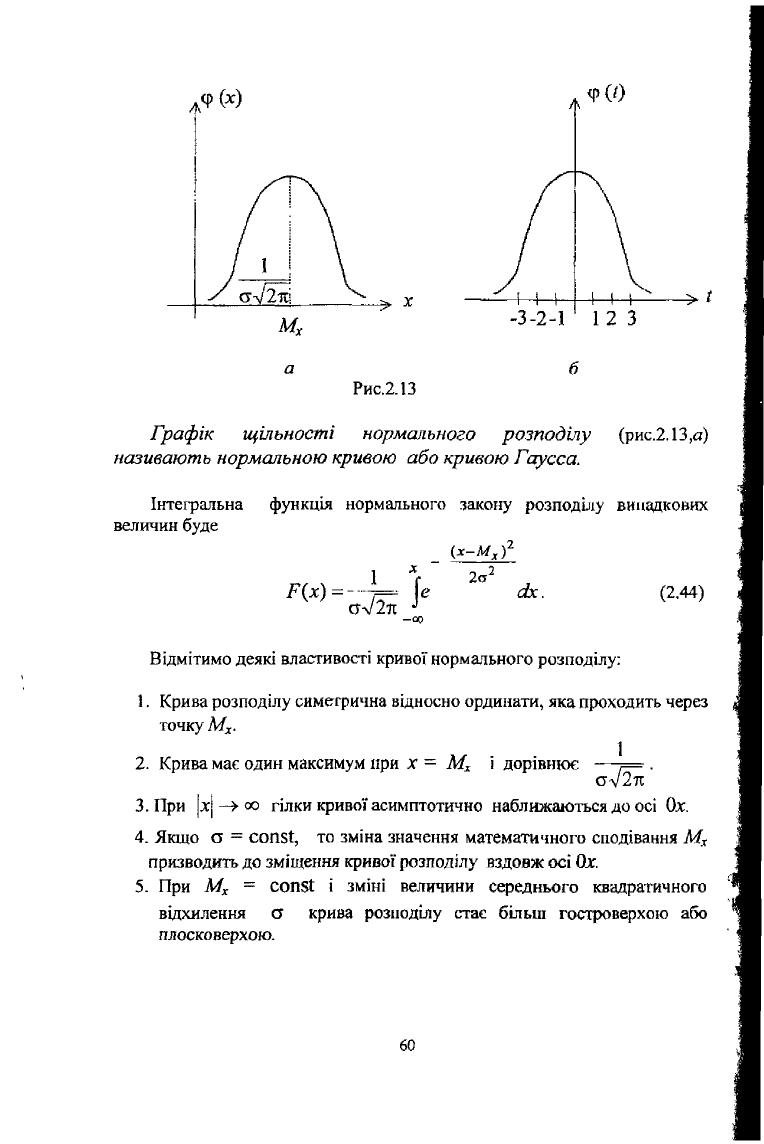
Крива нормального закону розподілу має симетричний горбхуватий

вигляд (рис.2.13,а)

(Х-М*)

(2-43)

<р(0

-3-2-1 1 2 3

Рис.2.13

Графік щільності нормального розподілу (рис.2.13,а)

називають нормальною кривою або кривою Гаусса.

Інтегральна функція нормального закону розподілу випадкових

величин буде

Відмітимо деякі властивості кривої нормального розподілу:

1. Крива розподілу симетрична відносно ординати, яка проходить через

точку М

2. Крива має один максимум ири х = М

і дорівнює .

3. При |.г|-»оо гілки кривої асимптотично наближаються до осі Ох

4. Якщо ст = const, то зміна значення математичного сподівання М

призводить до зміщення кривої розподілу вздовж осі Ох.

5. При М

= const і зміні величини середнього квадратичного

відхилення а крива розподілу стає більш гостроверхою або

плосковерхою.

dx. (2.44)

При вирішенні практичних задач, нормальний розподіл відіграє

важливу роль Якщо випадкова величина X підкоряється нормальному

закону розподілу, то ймовірність й попадання на ділянку

(СХ,

3) дорівнює

(х-М,)

1 Н 2о

Р ((X <х < р) = |ф(х)<& = \е ск

а а

(2 45)

Згідно з четвертою та п'ятою властивостями для різних випадкових

величин X буде своя крива розподілу Щоб уникнути цього визначають

нормований нормальний закон розподілу. Вводять нормовану

випадкову величину Ґ

х-М

= і, (246)

дтя якої математичне сподівання М, = 0, а середнє квадратичне

відхилення о, = 1

Тоді формули (2 43) та (2 44) для нормованого нормального закону

розподілу будуть маги вигляд

І 2

(2 4?)

л/2я

' і ' -V

Д0= = \е

Л (2 48)

Графік функції нормованої нормальної щшьносгз розподілу ф(ґ)

показано на рис 2 13,6 Він буде стандартним для будь-якої нормованої

випадкової величини

Інтеграл (2 45) не можна виразити через елементарні функції Тому

його обчислюють через спеціальну функцію, що є визначеним інтегралом

від величини е

(інтеграл імовірностей), для якого складені

таблиці (дод 1) Тобто

І І 2

<Р(0 =-4= [Є

' Ж (2 49)

л/

2л