Войтенко C.П. Математична обробка геодезичних вимірів. Теорія похибок вимірів

Подождите немного. Документ загружается.

де Рп(к) - ймовірність появи події к разів при и випробуваннях;

С„ число сполучень;

" (п-к)\к\

р - ймовірність появи події А в одному випробуванні;

- рівень значності події

в одному випробуванні.

Тоді

і=0 к=0

(1.37)

Так як члени формули (1.37) є членами розкладання бінома і

одночасно визначають ймовірність появи події' А при п випробуваннях

( п = 0,л), то сукупність ймовірностей Рп(к) називають

біноміальним розподілом ймовірностей (к =

0,1л

При значеннях п і к більше 10 розрахунки проводять з

застосуванням формули Стерлінга

л!«л/2ял

Збіг суми членів (1.37) з членами розкладання бінома дозволяє ввести

для обчислень ймовірностей можливого настання події А в серії п

незалежних випробувань добуткову функцію ф„(х):

<р*м = (я +рхУ - + с

„4"

{

рх +... +

+С

„д

+..Ар

х*. ^ (1.39)

Ця функція характерна тим, що коефіцієнт при х в розподіленні

(1.39) дорівнює ймовірності появи події А рівно к разів в серії із

п незалежних випробувань в перемінних умовах. Якщо ймовірність появи

події А, що проходить в неоднакових умовах в /-му досліді дорівнює

Р(А,) =р, і рівень значності Р(А

)-д„ то ймовірність того, що подія А

з'явиться рівно к разів в п незалежних випробуваннях буде дорівнювати

коефіцієнту при х* в розподіленні за степенями х добугкової функції

<Р. (*) = (<7І + РІХ) (42 + РІХ) -- (ЯП + РПХ). (1.40)

(1.38)

Приклад 1 Ймовірність виготовлення на автоматичному станку

нівелірних рейок дорівнює 0,90 Знайти ймовірність того, що із 10-ти

навмання взятих рейок 8 із них виявляться стандартними

Розв'язання. Виготовлення рейок проводиться в однакових умовах

Тоді за формулою (1 36) при л=10, к = 8, р = 0,90, а д =0,10

отримаємо

^10(8) = С,

(О,1)

(0,9)

=0,19.

Приклад 2. Знайти розподіл імовірностей числа прийомів виміру кута

при чотирьох незалежних прийомах, якіио ймовірність виміру кута в

одному прийомі дорівнює 0,9

Розв'язання. За умовами п — 4, р = 0,9, д = 0Л Використавши

формулу (1 39), отримаємо

(г) = (0,9 + 0,Іх)

= 0,1" х° + С\ 0,1

0,9У + с| 0,1

0,9У +

+ СІ -0,1

0,9

= 0,0001*° + 0,0036*' + 0,0486х

+ 0,2916х

+ 0,6561л:

Шукані ймовірності є коефіцієнтами біля

X*'

РАЮ)

= 0,0001; Р

(і) = 0,0036, Р

мг)

= 0,0486, Р

= 0,2916;

Рц4) = 0,6561

Перевірка. £ Р

4(4)

= 0,0001 + 0,0036 + 0,0486 + 0,2916 + 0,6561 = 1.

4=0

Як бачимо розв'язання вірне, а найбільш надійне число правильних

прийомів виміру кута дорівнює чотирьом

Приклад 3 Начальник парти, інспектор ВТК та головний інженер

контролюють результати топографічної зйомки Ймовірність виявлення

браку для начальника парти дорівнює 0,8, інспектора ВТК - 0,9 і

головного інженера - 0,6 Знайти ймовірність того, що два із них

виявлять брак

Розв'язання. Оскільки ймовірність для кожного контролюючого

різна, тобто випробування проходять в різних умовах, то застосуємо

добуткову функцію (І 40) Тоді прир, = 0,8, р

= 0,9, р

= 0,6 і д, = 02,

= 0,1, д

= 0,4 Отримаємо

<Нх) =• (0,2 + 0,8х) (0,1 + 0,9х) (0,4 + 0,6г) = 0,008х° + 0,272х

]

+ 0,288х

+ 0,432х

Коефіцієнт біля х

є шуканою ймовірністю Рц

) ~ 0,288

зз

МІЖ іншим, маємо найбільшу ймовірність того, що троє

перевіряючих знайдуть брак, так як ЛАД = 0,432

§ 9. Найбільш імовірне число появи подій при повторних

випробуваннях

Припустимо, що випробування проводяться в однакових умовах

Незаперечно, якщо однакові ймовірності появи подій, то при повторних

багатократних випробуваннях існує найбільш імовірне число появи події

Визначення. Найбільш імовірнім числом к появи події А в п

незалежних випробуваннях буде число, для якого ймовірність Р„

(

перевищує чи, в крайньому разі, не менше ймовірності із решти

можливих наслідків випробувань

Приклад 1 Проведено 8 прийомів виміру кута Ймовірність появи

плюсової чи мінусової помилки однакова і дорівнює р

—

0,5.

Знайти найбільш імовірне число появи плюсової помилки

Розв'язання. Так як незалежні виміри і проводяться в однакових

умовах, то ймовірності появи будь-якого числа появи плюсової помилки

можна знайти за формулою біноміального розподілу (135) або (1 39)

Тоді при и = 8

Таблиця 1 1

0 1

4 5

6 7 | 8

0,004

0,031

0,109

0,219

0,273

0,219

0,109

0,031

0,004

1,000

Відповідно до табл 1 1 найбільша ймовірність Р - 0,273 буде

супутньою для появи шуканої події при к

Разом з тим, якщо число випробувань п велике, то застосування

формули біноміального розподілу буде складним

Посилаючись на формулу (1 36) дещо спростимо розв'язання цієї

задачі Якщо в ряді багаторазових випробувань події є найбільш імовірним

число ко появи цієї події, то повинні виконуватися нерівності

(к

)>Р

(к

-1)]

За допомогою формули (136) після розкриття членів отримаємо

або

п1

к„ ^ я"-*""

п*о+1

(п-к

ук

Ч И

(п-к

-Щк

+\у

Після скорочень отримаємо

* ->

п-к

Ло+1

Розв язавши цю нерівність відносно Ао, отримаємо

ко>пр-д, (142)

так як (р + ч) = 1

Аналогічно із нерівності (141) отримаємо

(и-Ао)'Ао' (и-*ь+1)4*0-1)'

Після скорочення маємо

Р >. 1

п-к

+і'

або

ко< пр+р (143)

Тоді за формулою (1 42) і (1 43) маємо подвійну нерівність, що

служить для визначення найбільш імовірного числа к§

np-q < ко<пр +р (1 44)

Довжина інтервалу появи числа кц дорівнює одиниці Тому якщо

границі його є дробні числа, то маємо одне ціле число а якщо цілі, то

будемо мати два найбільші ймовірного числа подій - к$

Приклад 2. При вимірюванні ліній теодолітних полігонів імовірність

правильних вимірів окремих ліній дорівнює р

0,90 Знайти найбільш

імовірне число виміряних літи що відповідають вимогам точності

якщо в полігонах всього 150 ліній

Розв'язання. За умовами прикладу п = 150, р = 0,90, q І -р = 0,10.

Згідно з нерівностями (І 44) маємо

150 0,90 - 0,10 <

ко

< 150 0,90 + 0,90,

Звідкшчя 134,9 <ко< 135,9

Отже найбільш імовірне число правильно виміряних ліній буде

дорівнювати 135.

Запитання для самоперевірки

1 Що вивчає теорія ймовірностей

2 Дайте визначення подій Наведіть приклади

3 Які події називають випадковими

4 Що таке комплекс умов

5 Як ви розумієте повну групу подій

Наведіть приклад

6 Що називають частотою події

7 Приведіть класичне визначення ймовірності події В яких межах

змінюється ймовірність події

8 Що таке принцип практичної впевненості

9 При яких умовах виникає додавання і добуток складних подій

10 Сформулюйте теореми додавання ймовірностей

11 Які події називають залежними і незалежними

12 Що таке умовна та безумовна ймовірність

13 Сформулюйте теорему множення ймовірностей

14 Сформулюйте теорему додавання ймовірностей для сумісних подій

15 Напишіть формули повної ймовірності та ймовірності гіпотез

(Бейєса)

16 В яких задачах виникає необхідність застосування формул повної

ймовірності та ймовірності гіпотез

17 Коли застосовують формулу Бернуллі

18 Приведіть формулу появи к-оі події при п незалежних

випробуваннях

19 Напишіть формулу добуткової функції ф„(х) настання події А в

серп п незалежних випробуваннях

20 Який вигляд має добуткова функція ймовірностей появи подій, коли

випробування проходять в неоднакових умовах

21 Як визначити найбільш імовірне чисто появи подій при повторних

випробуваннях

РОЗДІЛ 2. ВИПАДКОВІ ВЕЛИЧИНИ, ЇХ ХАРАКТЕРИСТИКИ І

ЗАКОНИ РОЗПОДІЛУ ЙМОВІРНОСТЕЙ

§ 1. Випадкові величини

Випадкові події якісно характеризують випадковий результат

проведеного досліду. Разом з тим випадковий результат можна

характеризувати і кількісно.

Випадковою величиною називають таку величину, яка в

результаті досліду може набути будь-якого довільного значення

до того заздалегідь невідомо якого саме.

Поняття випадкової величини є одним із важливих понять теорії

ймовірностей. Позначимо випадкові величини великими буквами

латинського алфавіту — X, У, ..., а їх можливі значення позначимо

відповідними малими буквами х, у, ....

Випадкові величини в практичній діяльності можуть бути дискретні та

неперервні.

Дискретною (перервною) випадковою величиною

називають таку величину, яка може приймати окремі кінцеві

значення або їх нескінченну кількість (безліч, елементи якої

можуть бути занумеровані).

Приклади дискретних випадкових величин·.

Кількість правильних вимірів кута при 10 прийомах.

Число бракованих приладів в партії із п штук.

Неперервною випадковою величиною називають таку

величину, можливі значення якої повністю заповняють деякий

інтервал ( кінцевий або нескінченний) числової осі. Таким чином і

число можливих значень неперервної випадкової величини буде

нескінченним.

Приклади

неперервних

випадкових

величин:

1 •

Помилка виміру

довжини лінії,

чи

величини

кута.

2. Графік рівня води в річці, отриманий за

допомогою

реєстраційного

автоматичного приладу.

Цілком зрозуміло, що при випробуваннях окремі значення випадкових

величин помітно відрізняються одне від одного і на перший погляд вони не

здаються неперервними. Але треба усвідомити, що ці значення не можна

перечислити заздалегідь і мова йде про ті значення, які можна прийняти в

результаті досліду. Появу того чи Іншого значення не можна заздалегідь

задати точно, але можна шукати ймовірності того чи іншого значення

випадкової величини. Це означає, що випадкова величина володіє

ймовірністю її появи. Тому в практичній діяльності зручніше

користуватися дискретними випадковими величинами ніж неперервними

випадковими величинами.

§ 2. Закон розподілу ймовірностей випадкових величин

В результаті досліду неперервна випадкова величина X приймає

одне із своїх можливих значень. Тобто з'явиться одна подія із повної групи

несумісних подій: X - Хь X — Хі , .-.. , X = х„. Кожне із цих значень

володіє ймовірністю появи, або

Р(Х=

Х]

)=р

Р(Х = х

)=р

,,.., Р(Х = х

)=р

. (2.1)

Так як всі можливі події утворюють повну групу несумісних подій, то

сума ймовірностей всіх можливих значень випадкової величини X

дорівнює одиниці

£/>(*=*,) = 2>, = і-

/=1 ;=і

Цілком зрозуміло, що випадкова величина буде повністю визначена,

якщо вказати ймовірність кожної із подій (2,1).

Законом розподілу випадкової величини називають всяке

співвідношення, що встановлює зв 'язок між можливими

значеннями випадкової величини і відповідними ймовірностями.

Закон розподілу дискретної випадкової величини задають:

1) аналітично;

2) чисельно у вигляді таблиці;

3) графічно.

Аналітично закон розподілу для дискретних випадкових величин

задають за допомогою формул розподілу ймовірностей ири повторних

випробуваннях (1.35; 1.37; 1.39). Ймовірність появи к-ої події при п -

випробуваннях розраховують за формулою (1.36). Приклад аналітичного

розрахунку розподілу ймовірностей наведено в розд.1, § 8 (табл.1.1).

Найбільш просто закон розподілу дискретної випадкової величини X

відображають у вигляді таблиці, яку називають рядом розподілу

випадкової величини.

Таблиця 2.1

Хі

Хг

Хп

р.

Рі

Р2 Рп

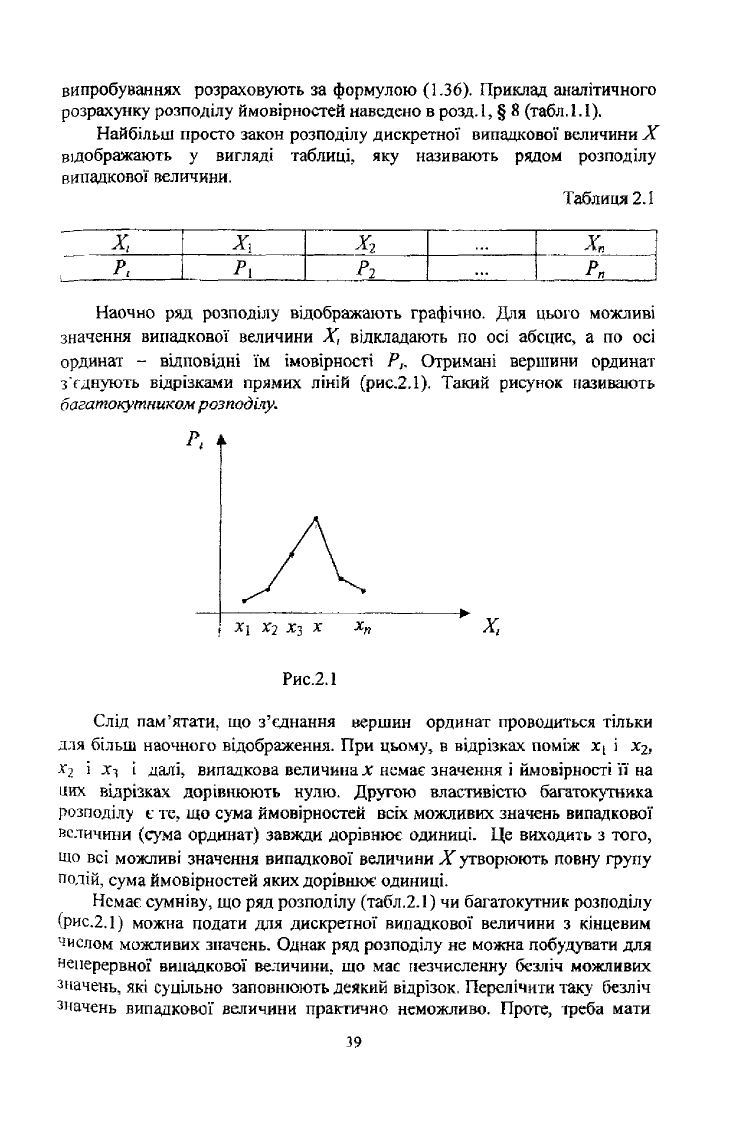
Наочно ряд розподілу відображають графічно. Для цього можливі

значення випадкової величини X, відкладають по осі абсцис, а по осі

ординат - відповідні їм імовірності Р,. Отримані вершини ординат

з'єднують відрізками прямих ліній (рис.2.1). Такий рисунок називають

багатокутником розподілу.

Рис.2.1

Слід пам'ятати, що з'єднання вершин ординат проводиться тільки

для більш наочного відображення. При цьому, в відрізках поміж х

(

і х

і х^ і далі, випадкова величина * немає значення і ймовірності її на

них відрізках дорівнюють нулю. Другою властивістю багатокутника

розподілу є тс, що сума ймовірностей всіх можливих значень випадкової

величини (сума ординат) завжди дорівнює одиниці. Це виходить з того,

що всі можливі значення випадкової величини X утворюють повну групу

подій, сума ймовірностей яких дорівнює одиниці.

Немає сумніву, що ряд розподілу (табл.2.1) чи багатокутник розподілу

(рис.2.1) можна подати для дискретної випадкової величини з кінцевим

числом можливих значень. Однак рад розподілу не можна побудувати для

неперервної випадкової величини, що мас незчисленну безліч можливих

значень, які суцільно заповнюють деякий відрізок. Перелічити таку безліч

значень випадкової величини практично неможливо. Проте, треба мати

таку характеристику розподілу ймовірностей, яка б відображала як

дискретні, так і неперервні випадкові величини. Нею є функція розподілу.

Функцією розподілу або інтегральним законом розподілу

випадкової величини X називається задания ймовірності події

виконання нерівності X < х, де х - деяка поточна змінна. її

розглядають як функцію аргументу .V і визначають за формулою

F(x)-P(X<x). (2.2)

Функцію розподілу Мх) називають інтегральною функцією

розподілу або інтегральним законом розподілу. Вона мас досить

просту геометричну інтерпретацію. Розглянемо випадкову величину, як

випадкову точку X осі ОХ (рис.2.2), іцо в результаті випробування може

прийняти те чи інше положення. Тоді функція розподілу F(x) є

Ймовірністю того, що випадкова точка X в результаті випробування

попаде зліва від точки х.

Р(х) - Р(Х< х)

—і н

0 X

—, ^—

Рис.2.2

Функція дискретної випадкової величини X, що може приймати

значення Х\, Х2,..

,х„ буде мати вигляд

F(x)= ^Р(Х=х,). (2.3)

X, <1

При цьому додавання ймовірностей розповсюджується на всі можливі

значення випадкової величини, які за своєю величиною менші аргументу х.

Це означає, що функція розподілу дискретної випадкової величини X

розривна і зростає стрибками при переході через точки можливих її

значень Х\, х

,..., х„.

Приклад 1. Побудувати функцію розподілу появи плюсових похибок

вимірів кута із 8-ми прийомів, якщо ймовірність її появи в кожному

прийомі дорівнює р = 0,5.

Розв'язання. Ряд розподілу ймовірностей розраховано за формулою

(1.35) і значення його приведено в табл. 1.1.

За допомогою формули (2.3) побудуємо функцію розподілу випадкової

величини X - К. Тоді

2. При 0 <х < 1 (0<^<1) Г(х)= ^Р(Х = х,)=Р(Х=0) =

••=

0,004.

і.При \ <х<2 Е{х)=^Р{Х^х^ = Р{Х=0) + Р{Х^\) =

- 0,004 + 0,031 = 0,0035.

4 .При 2 < х < З Я*) = 0,144. 5. При 3<х<4 Я*) = 0,363.

6. При 4<х<5 Нх)= 0,637. 7.При 5<х<в Р(х) =0,856.

8. При 6 <х < 7 Дх) = 0,965. 9. При 7<х<8 ^(х) = 0,996.

10. Яри х > 8 Л[х) = 1,0.

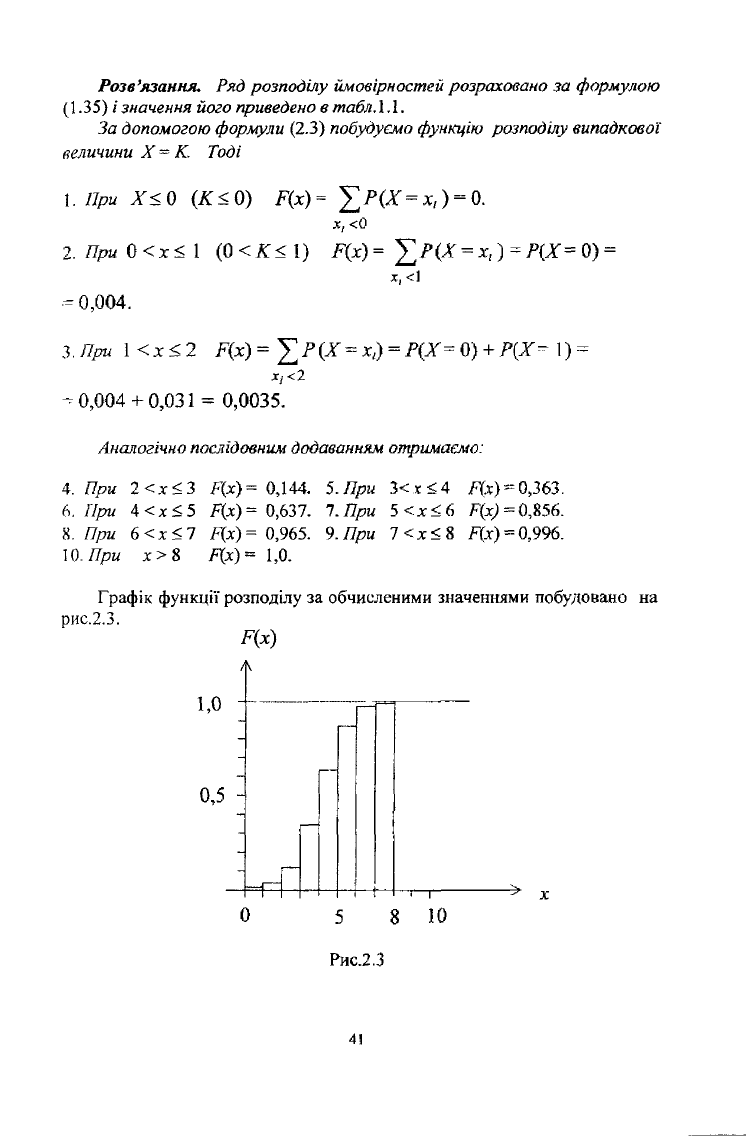
Графік функції розподілу за обчисленими значеннями побудовано на

1. При Х<0 (К< 0) Р(х)= ^Р(Х = х,) = 0.

*, <0

Аналогічно послідовним додаванням отримаємо:

рис.2.3.

1,0

0,5 -

5 8 10

Рис.2.3