Войтенко C.П. Математична обробка геодезичних вимірів. Теорія похибок вимірів
Подождите немного. Документ загружается.


Іноді приводять таблицю функції 2<р(/) для обчислення ймовірності
попадання нормально розподіленої випадкової величини X в симетричні
інтервали від -X до X, Значення інтегральної функції (формула 2.48)
приведено в дод. 2.
Функцію
©(?)
називають нормованою функцією Лапласа або
інтегралом імовірностей. Тоді формула (2.45) буде
Р ( <х < х < Р);
г -
1
'
2
% 2
-J2n
dt.
І
(я формула після перетворення набуде вигляду
(2.50)
Р( а <х <3) = Ф
J
(Х-а
'х ;
(2.51)
При цьому функція Лапласа має властивості:
1) ф(0) = 0; 2) ф(-оо) = -0,5; 3) ф(+°о) = +0,5; 4) ф(-/) = ф(Г). Якщо
а = -р, то
П-Р <* <Р ) = 2ф(Р).
При t
2
= |fi| = t
P(-t <x < /) = 2ф (0· (2.52)
Інтеїральну функцію F(t) можна визначити через функцію Лапласа
співвідношенням
F(i) = 0,5 + <p(f). (2.53)
Це означає, що функція FtJ) — це площа під кривою ф(^),
відмежована справа абсцисою t.
Підставимо формулу (2.53) у вираз Р( а <х < Р) = P{t\ <t < t
2
)
:
= F (І?)
—
/<(0, отримаємо
р(а <х < Р) = ф (ґ
2
) - Ф (i,)· (2.54)
Якщо відсутні таблиці значень функції ф(ґ) (дод. 1), то її обчислюють
за формулою
[ t t
S
t
1
ф(0 = 0,798 г + —+ ..
6 40 336
л
J
(2.55)
62

Приклад 1 Помилки вимірів ліній світловіддалеміром підкоряються
нормальному закону розподілу Математичне сподівання результатів
багаторазових вимірів лінії полігонометрії дорівнює М
х
= 245,037 ад.
Середнє квадратичне відхилення дорівнює
<т —
10 ми Знайти ймовірність
,пого, що результати виміру лінії будуть в інтервалі від (*= 245.018 м бо
р- 245.058 м.
Розв'язання. За формулою (2.46) обчиспимо нормовані величини
а -М 245018-245038 „
г, = *- = = -2;
а 10
{ а
Р-м
л
_ _ 245058 -245018
=
Н
а " " 10 '
Гак як |/)| 2, то за таблицею значень функції ф(/) ~ 0,4772
( дод 1) і за формулою (2.52) знайдемо
Р(-2<і < 2} = 2ф(0 = 2
•
0,4772 = 0,954.
Приклад 2. Згідно з вихідними даними прикладу І, знайти симетричні
граничні чначення
<Х
та (3 результатів вимірів з імовірністю Р = 0,90
відносно математичного сподівання
Розв'язання. За формулою (2.52) при
<Х
= -
[3
маємо
Р{а
<
х < р) - 2ф(Р) =
2ф(Г)
= 0.90.
За таблицями інтегральної функиіі (дод 2) знаходимо величину
<
при
Р ~ 0,90. Вона дорівнює 1.3. При симетричності граничних значень
а ~М
£ і = 1,3. Тоді за формулою (2 46) обчислюємо -і = — , або
а
« = М
х
-іа = 245,038 м- 1,3 10 мм = 245,025 м;
, або \3 = М
х
-Ю =245,038+ 1,3 · 10мм = 245,051 м.
а
У порівнянні зі значеннями інтервалів а і р в прикладі 1 бачимо,
зменшення ймовірності Р призводить до звуження значень інтервалу
Рєзучьтатів вимірів лінії
63
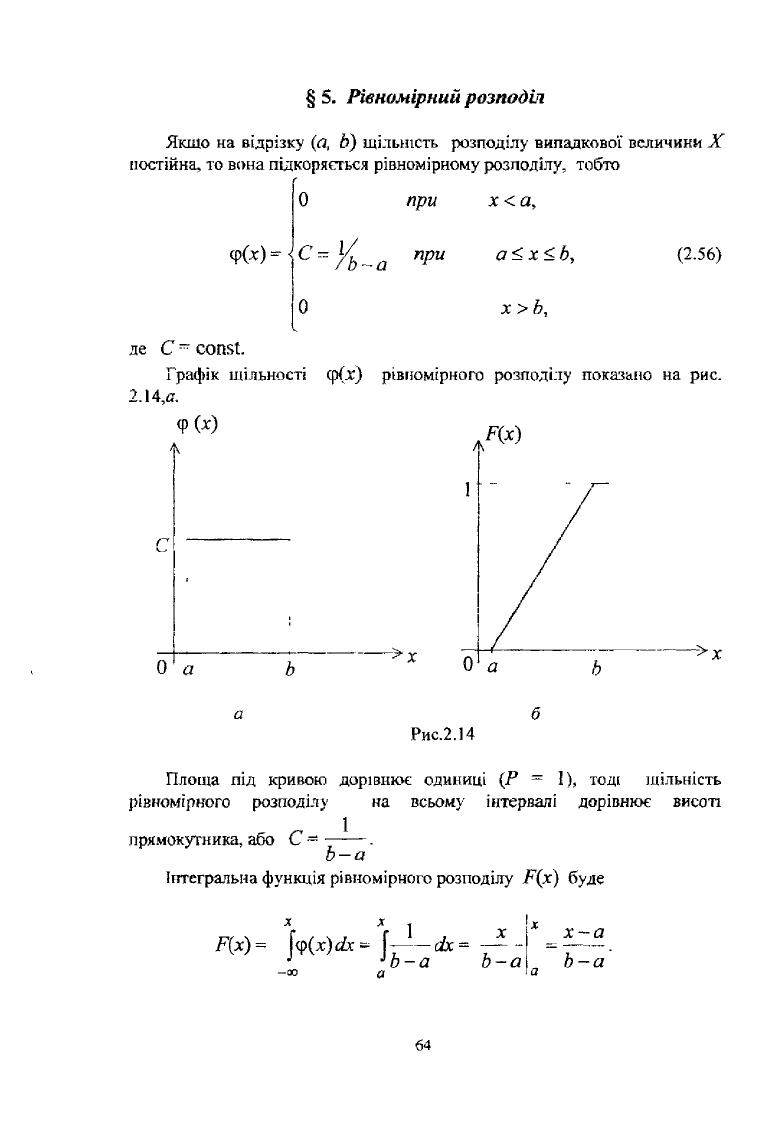
§ 5. Рівномірний розподіл
Якщо на відрізку (а, Ь) щільність розподілу випадкової величини X
постійна, то вона підкоряється рівномірному розподілу, тобто
ф(х)
=
0
С - ^
0
при
b-а "Р
и
х<а,
а<х<Ь,
х>Ь,
(2.56)
де С= const.
Графік щільності ср(.ї) рівномірного розподілу показано на рис.
2.14,д.
Ф
(*)
0 а
Рис.2.14
Площа під кривою дорівнює одиниці (Р ~ 1), тоді щільність
рівномірного розподілу на всьому інтервалі дорівнює висоті
прямокутника, або С ~ .
Ь-а
Інтегральна функція рівномірного розподілу Р(х) буде
X X J
Fix)
=
[ф(х)Л
=
І dx
=
—
J J
b-a h-
х-а
b-a\ b-a
і a
64

Так як х < а ^(х) = 0, а при х > Ь Дх) =
1,
то
0 при х<а\
Кх) =
х-а
при а<х<Ь\
при х>Ь.
(2.57)
Графік функції Р(х) показано на рис. 2.14,6. Таким чином, якщо
випадкова величина підкоряється закону рівномірної щільності на деякому
інтервалі (а, Ь), то це означає, що поява будь-яких значень випадкової
величини в межах цього інтервалу однаково ймовірні мають одну і ту ж
щільність імовірності.
В геодезії помилки заокруглення відліків по шкалах приладів до цілих
ііодіяок розглядаються як випадкові величини, що мають однакову
щільність імовірності будь-якого значення між двома сусідніми цілими
поділками.
Математичне сподівання та дисперсія рівномірного розподілу
дорівнюють
М
Г
= Г—-А = ——!
>Ь-а 2 (Ь-а)).
а
+
Ь
(2.58)
Дг
Ь-а 12
(2.59)
причому
Позначимо точність відліку по тикалі приладу через <Х
= - (Ь - а). Тоді стандарт рівномірного розподілу буде дорівнювати
Ь-а _ а
(2.60)
Відомо, що інтервал шкали оптичного мікроскопа теодоліта ТЗО
Дорівнює одній хвилині. Тоді Р
— 0£
= 1'; (Х-0',5, а стандарт відліку
(формула 2.60) буде дорівнювати
а
°'
5
~ п' *
<у_ = = -т= « 0,3.
* л/3 л/3
65

Рівномірний розподіл в геодезії використовується при вирішен"
задач оцінки точності результатів вимірів пов'язаних із їх заокругленням
§ X
2
-розподіл
При обробці геодезичних вимірів використовують ряди квадрат
нормально розподілених випадкових величин х.
І
Ірипустимо. що з ряду нормально розподілених випадкових величі
А"|, А'), ... Х„ утворимо ряд нормованих незалежних випадкових величі
Zі, Хъ її, де к число ступенів вільності. Вони також буду
нормально розподіленими з математичним очікуванням М
2
—
0.
Якщо
;=1
то в математичній статистиці доведено, що щільність розподй
випадкової величини визначається за формулою
4-і Л
у2
е
2
у
ф(У)=-, , (2.«
-
де Г((Х) - гама-фупкція, яка визначається за допомогою інтеграї
Л.Ейлера.
Наприклад. Г(0( + 1) " а Г(а); Г(а) Г(1 -а) = —
этттв
причому Г(а +1) - (X!; Г( 1) = 1; Г(0,5) = ^ТТ; Г(0£+ ~) =
= 1^.(20^
2
1
2
а
і
Графік щільності ймовірності х-розподілу показано на рис.2.15. '
Математичне сподівання, дисперсія та стандарт випадкової величні
У
дорівнюють ;
М
у
= к; Оу = 2к\
<у
у
= 4ік. (2.6ІІ
X - квадрат (%
2
) розподіл використовують для оцінки точное
дисперсії та стандарта при математичній обробці результатів вимірів.
66
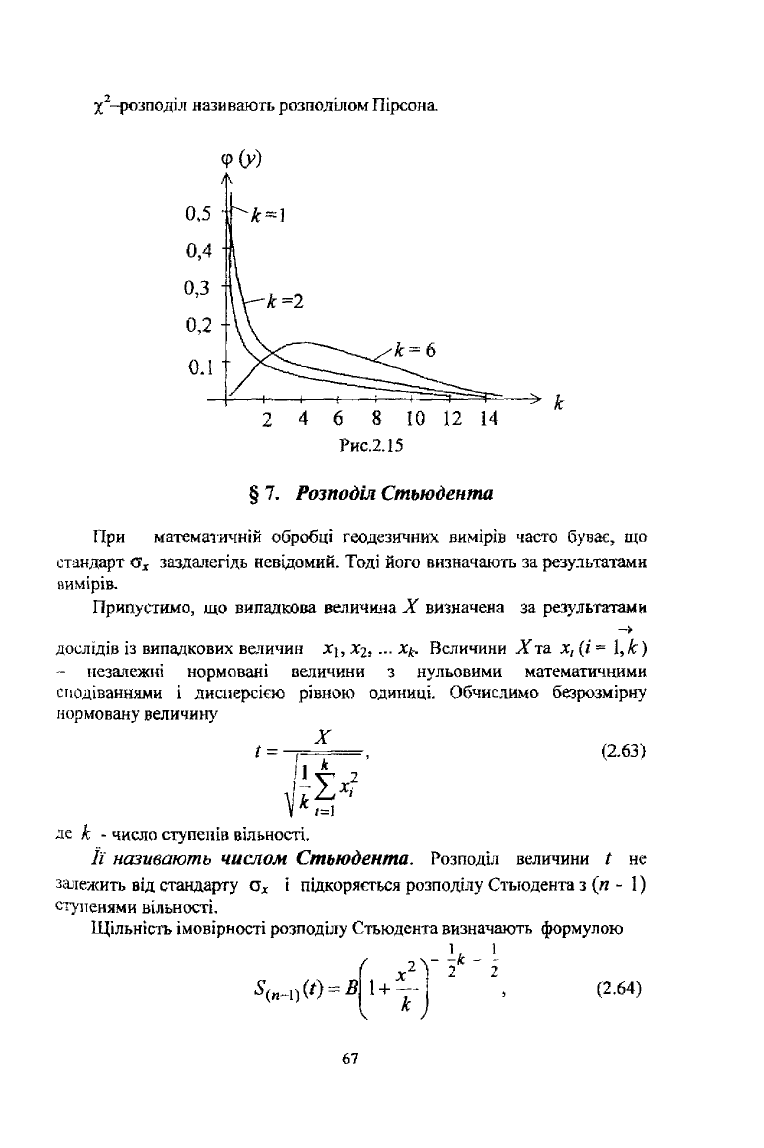
%
2
-розподіл називають розподілом Пірсона.
Ф(У)
0,5 ^ = 1
0,4
0,3
0,2
0.1 "
к
2 4 6 8 10 12 14
Рис.2.15
§ 7. Розподіл Стьюдента
При математичній обробці геодезичних вимірів часто буває, що
стандарт
<У
Х
заздалегідь невідомий. Тоді його визначають за результатами
вимірів.
Припустимо, що випадкова величина X визначена за результатами
дослідів із випадкових величин Х\, х
2
,... Хь Величини Xта. х, (і = 1 ,к)
- незалежні нормовані величини з нульовими математичними
сподіваннями і дисперсією рівною одиниці. Обчислимо безрозмірну
нормовану величину
де к - число ступенів вільності.
Її називають числом Стьюдента. Розподіл величини / не
залежить від стандарту О
х
і підкоряється розподілу Стьюдента з (и - 1)
ступенями вільності.
Щільність імовірності розподілу Стьюдента визначають формулою
->
X
(2.63)
і-
(2.64)
67
де
В
Г(0,5£ + 0,5)
Г(0,5)а/тг£
Крива функції щільності і розподілу ф(х) симетрична відносно осі
ординат, так як математичне сподівання А/(/) = 0. її називають
законом Стьюдента з к ступенями вічьності. При достатньо
великих значеннях к, крива розподілу Стьюдента досить близька до кривої
нормального розподілу випадкових величин. Причому
(
1 + —
V
-І*
2
2
Тоді формула (2.64) набуває вигляду
ф(х)=
тк
е
~х
2
2
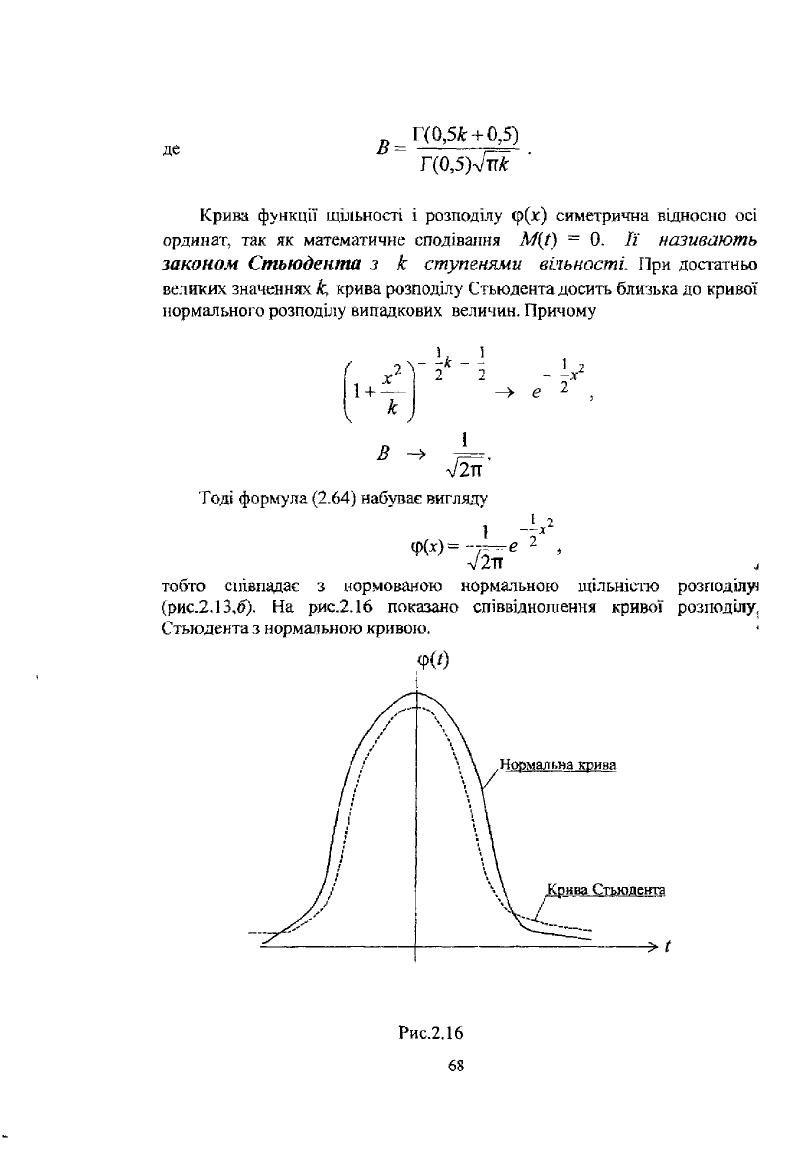
тобто співпадає з нормованою нормальною щільністю розподілу!
(рис.2.13,б). На рис.2.16 показано співвідноліення кривої розподілу,
Стьюдента з нормальною кривою.
Нормальна крива
Рис.2.16
68

Розподіл Стьюдента використовується для оцінки точності
результатів геодезичних вимірів, коли їх число не досить велике
(обмежене).
Запитання для самоперевірки
1. Що називається випадкового величиною?
2. Дайте визначення та покажіть геометричний зміст неперервних та
дискретних випадкових величин.
3. Що називають законом розподілу випадкових величин?
4. Приведіть приклади закону розподілу випадкових величин.
5. Дайте визначення функції розподілу та назвіть її властивості.
6. Приведіть формулу га властивості щільності розподілу неперервної
випадкової величини.
7. Запишіть формулу обчислення ймовірності попадання випадкової
величини в інтерват.
8. Яка різниця між графіками функцій розподілу та щільності
розподілу неперервної та дискретної випадкової величини?
9. Дайте визначення математичного сподівання, дисперсії, початкового
і центрального моментів.
10. Що таке мода та медіана?
11. Що називають середнім квадратичним відхиленням випадкової
величини?
12. Приведіть формули числових характеристик розподілу для
неперервних та дискретних випадкових величин.
! 3. Порівняйте властивості математичного сподівання та дисперсії.
14. Що таке асиметрія та ексцес? Як вони позначаються на графіку
нормального розподілу?
15. Який розподіл випадкової величини називають нормальним
розподілом?
16. Які властивості кривої нормального розподілу?
17. Що називають функцією Лапласа і які її властивості?
18. Який розподіл випадкової величини називають рівномірним
розподілом?
19. Чому дорівнюють: математичне очікування, дисперсія та стандарт
рівномірного розподілу?
20. Коли використовують //'-розподіл?
21
.При яких умовах використовується /-розподіл Стьюдента?
69

РОЗДІЛ 3. СИСТЕМИ ВИПАДКОВИХ ВЕЛИЧИН. 1ТАНИЧНІ
ТЕОРЕМИ ТЕОРІЇ ЙМОВІРНОСТЕЙ
§ 1. Поняття та закон розподілу системи випадкових величин
До цього часу ми розглядали одномірну випадкову величину X.
Однак в сучасній теорії математичної обробки результатів багаторазових
повторних геодезичних вимірювань використовують багатомірні випадкові
величини. Багатомірна випадкова величина може складатися із декількох
компонентів і бути двомірною, тримірною і так далі. Так, наприклад,
координати точки на площині визначаються двома випадковими
величинами: абсцисою X та ординатою У; положення точки в просторі
визначається вже трьома координатами - X, У та висотою Н.
Сумісна дія двох чи більше випадкових величин приводить до
системи випадкових величин. Умовимось систему декількох випадкових
величин X, У, .... N позначати (X, У, ..., .¥)• При вивченні системи
випадкових величин визначають характеристики як кожної випадкової
величини, так і зв'язки та залежність між ними. А це вже більш складні
задачі.
Домовимось, що систему двох випадкових величин (X, У) ми будемо
розглядати як випадкову точку на площині хОу з координатами X
і
У. або
як випадковий вектор на площині з випадковими складовими X і У.
Систему трьох випадкових величин (X, У, 2) - як випадкову точку в
тримірному просторі або, як випадковий вектор в просторі. За аналогією,
систему п-випадкових величин (X, У, .. , А
г
) розглядають як випадкову
точку в н-мірному просторі або, як «-мірний випадковий вектор.
Законом розподілу системи випадкових величин
називають співвідношення, що встановлює зв'язок між
областями можливих значень системи випадкових величин і
ймовірностями появи їх в цих областях.
Закон розподілу системи випадкових величин можна задавати в різних
формах. Покажемо табличний спосіб розподілу системи дискретних'
випадкових величин.
Якщо X та У - дискретні випадкові величини, значення яких
->
дорівнюють (ХрУ^, де і = (1 ,п), а у = (1 ,т), то їх розподіл системи
можна характеризувати ймовірностями р
и
= Р(Х = х,: У ~ })). Це
означає, що коли випадкова величина X приймає значення х„ одночасно і
величина У прийме значення у
}
.
70

Ймовірність Ру зводять до табл. 3.1. Її називають таблицею розподілу
системи двох дискретних випадкових величин
Таблиця 3.1
х\
Х2
Х
П
..
Уг
Ріг
_ і>2_1
Рп\
..
Уг
Ріг
Рц
Р„2
у
т
Ріт Ріт 1 Рпт
Всі можливі події (X = А-,; V -- у,) при і = (1 ,гі) і у = (\.т)
скіадають повну групу несумісних подій і тому
^Р(Х = х„ Г = (3.1)
У У
§ 2. Система двох випадкових величин
В практиці геодезичних вимірів досить часто взаємодіють дві
випадкові величини X та У. тобто двомірні випадкові величини. В
попередньому параграфі ми наводили приклад з координатами точки.
При лінійних вимірах взаємодіють — довжина мірного приладу та
температура. При дослідженнях деформацій інженерних споруд
взаємодіють - величина осідання та інтервал часу і так далі.
Закон розподілу системи двох випадкових величин задають функцією
ротюілу та щільністюрозподиіу.
Функцією розподілу системи двох випадкових величин
називають функцію двох аргументів Р{х,у), що дорівнює
ймовірності сумісного виконання двох нерівностей X < х < у,
тобто
Р\х,у)=Р{Х<х і Г< у). (3.2)
Геометрично функцією розподілу системи двох випадкових величин є
ймовірність попадання випадкової точки {Х,Т) в нескінченний квадрат
площини (рис.3.1) з вершиною в точці (х,у)·
71
