Войтенко C.П. Математична обробка геодезичних вимірів. Теорія похибок вимірів

Подождите немного. Документ загружается.

Оскільки функція розподілу дискретної випадкової величини

виглядає як сходинкова ламана лінія, тому її називають

сходинковим графіком.

Якщо випадкова величина неперервна, то вона має ймовірність в

кожній точці осі х Згідно з формулою (2.3) функція розподілу буде

зростати поступово, тому шо можливі значення випадкової величини

неперервно заповнюють будь-який інтервал на осі х. Тоді графік

виглядатиме як монотонно зростаюча функція розподілу Р(х) на

інтервалі від а до Ь (рис.2.4).

Ях)

Функція розподілу мас властивості:

1. Функція розподілу Fix) є зростаючою і міститься між нулем та

одиницею

0 < F(х) < 1. (2.4)

Це випливає з того, що функція F(x) визначається як імовірність

випадкової події Х<х.

2. Ймовірність виникнення випадкової величини в інтервалі від СК до (і

дорівнює різниці значень функції на кінцях інтервалу

Р(а <х<р) =/?(Р) -F(0(). (2.5)

Визначимо подію А (рис.2.5) того, що випадкова величина х < 0! та

подію В для випадку х < |3.

P(B)

Подія С відображає те, що Ot < х < ß В цьому випадку подія В буде

складатися із суми двох, несумісних подій А і С, тобто

В = А + С.

Зпдно з теоремою додавання ймовірностей маємо

РІВ) = Р(А) + Р(С)

Разом з тим Р(А) = F (х < a) = F( <Х), Р(В) = Fix < ß) = f'(ß)

, P(C) = P(<X <x<ß)

Тому

/<(ß) = F{a) + P (<x <

< ß), (2 6)

a i

(a<x<ß)= F(ß)-F(a)

Припустимо, що ß —> <X. Тоді в формулі (2 5) будемо мати

Р(х = а) = hm (а < X < ß) = lim - /"(а)]. (2 7)

ß-->« ß-мх

Якщо функція в точці Of неперервна, то граничне значення дорівнює

Hviro При розриві функції в точці (X й граничне значення буде

дорівнювати значенню стрибка функції F(x)

З цього робимо висновок, що ймовірність випадкової

величини в точці для неперервної функції дорівнює нулю Це

явище називають парадоксом теорії ймовірностей.

Проте нульова ймовірність події лише зазначає, що частота цієї події

невпинно спадає при збільшенні числа дослідів, однак це не означає, що ця

подія неможлива

З Функція розподілу випадкової величини є зростаючою функцією,

тобто при ß> Ot

F(ß) >F(tX) (2 8)

Згідно з (2 6) маємо

ЯР) = ДСС) + Р(а <лг < Р)

Гак як імошршсгь будь-якої події £ додатне число, то

Р(<х <х<Р)>о

З На мінус нескінченності функція розподілу дорівнює нулю, а на

плюс нескінченності - одиниці, тоб го

F(- <ю) = 0, F(+x)

(2 9)

Це цілком вірно, так як при необмеженому переміщенні точки X

вліво, попадання випадкової точки X лівіше х максимально стає

неможливою подією і F(-ю <х ) = 0. В той же час при необмеженому

переміщенні точки х вправо ноиадання випадкової точки X зліва під х

практично стає достовірною подією,тоді F(x < +оо) ~ 1

За допомоіою функції розподілу можна знайти ймивірнісіь

випадкової величини в будь-якому шгсрвалі або u кожній точці можливих

значень для дискретної випадкової величини Тому функція розподілу

однозначно визначу закон розподілу випадкової величини

Приклад 2. Функція розподілу неперервної випадкової величини X

задана виразом

F{x) =

а(х+7)

при х <~2,

при - 2

X < + 2,

при х > 2

Знайти коефіцієнт а та побудувати графік функції F(\)

Визначити ймовірність появи випадкової величини в інтервалі ( 0, +2)

Розв'язання. Скористаємося тим, що функція розподілу випадкової

величини X неперервна і при х

2 дорівнює одиниці, тоді а(х + 2)

;

=1. и

а - — Ірафік функції F(x) зображено на рис 2 6

Рис.2.6

Відповідно до другої властивості функції розподілу за формулою (2.5)

маємо

/>( 0 < х < 2) = F (2) -F(0) = — (2 + 2)

- — (0 + 2)

= 0,75.

16 16

Більш наочно характер розподілу неперервної випадкової величини в

невеликих інтервалах числової осі х дає функція щільності розподілу

ймовірностей або диференціальний закон розподілу.

Якщо маємо функцію розподілу Fix) випадкової величини Х

то

ймовірність попадання її на елементарну ділянку (х, х + Ах) згідно з

формулою (2.5) буде:

Р(х <X

х + Дх) = Fix +Дх) - Fix).

Знайдемо середню ймовірність, що припадає на одиницю

довжини ділянки Ах

Р(х<Х <х + Ах)

F(x + Ах) - F(x) ^

{

Дх Лх

Перейдемо в рівності (2.10) до граничного значення при 0

,· Р(х<Х<х + Дх) F(x + Ax)-F(x) . , ,

lim і = hm - ^ • /- = F ix) = /= ФУ

Дх Дх—>о Дх

(2.11)

Функцією щільності розподілу випадкової величини в

точці х є граничне відношення ймовірності попадання її на

елементарну ділянку від х до х + Лх до довжини цієї ділянки Лх,

копи Лх наближається до нуля

Її позначають Дх) або ф(х). Зміст функції щільності розподілу ф(х)

полягає в тому, що вона вказує, як часто з'являється випадкова величина

X навколо точки х при повторенні дослідів.

Якщо комплекс умов при проведенні дослідів помітно не

змінюється, то графік функції щільності розподілу для

неперервної випадкової величини має вигляд, зображений

рис 2.7,іа Його називають кривою розподілу.

ср(х)

л ф(х)

-П-

П-

-4-3-2-1 0+1+2+3+4

а б

Рис.2.7

Для дискретних випадкових величин маємо гістограму розподілу

(рис.2.7,б).

Функція щільності розподілу має властивості:

1. Щільність розподілу невід'ємна, тобто

ф(х) >0. (2.11)

2. Функція розподілу випадкової величини дорівнює інтегралу від

функції щільності в інтервалі від - со до х

Р{х) = |ф(х)б/х.

(2.12)

3. Ймовірність попадання неперервної випадкової величини X на

відрізку ((X, Р) дорівнює інтегралу від функції щільності розподілу,

взятому за кінцевими значеннями цього відрізка

Р(а<х<3) = | ф(х)Л. (2.13)

Геометричний зміст цього результату полягає в тому, що ймовірність

появи випадкової величини в інтервалі від (X до р дорівнює площі

криволінійної трапеції, заштрихованої нарис.2.7

4 Інтеграл в нескінченних межах від -

«>

до + оо дорівнює одиниці

+»

1. (2 14)

I ф

(де)

сіх

Ймовірність попадання випадкової величини X на елементарний

інтервал сіх з точністю до нескінченно малих вищого порядку чим Ал'

дорівнює о(х) сіх (так як АР (де) * еіР'(х) =

<5)(х)сіх).

Геометричний зміст

цього виявляється в тому, що це є площа елементарного прямокутника з

висотою ф(х) і основою сіх. Величина ф(х)с£с називається

елементом імовірності

Приклад 3 Випадкова величина X підкоряється закону розподілу зі

щільністю

х<0

ф(х)-<{а5Іп2х 0<х<—,

—.

Потрібно 1) Знайти коефіцієнт а 2) Побудувати графік щільності

розподілу 3) Обчислити ймовірність попадання випадкової величини на

ті

інтервал від 0 до —.

Розв'язання. 1) При визначенні коефіцієнта а скористаємось 4-ою

властивістю функції щільності розподілу

| ф(дс)Л-1, тоді

ВІП

2хсіх --2а

СОЇ

2Х =4а=1,

-00 0 'о

або

а= —.

2) Графік щільності розподілу ф(х) зображено нарис.2 8

» X

3) За

формулою (2.13)

маємо

Р(0< х <-) = Г

—

5'т2хсіх = —соз2х

а' J А і

1 71

- (СОБ

—

- соз 0) = 0,5.

§ 3. Числові характеристики випадкових величин

Закон розподілу повністю характеризує випадкову величину з точки

зору ймовірності її появи в будь-якому інтервалі числової осі Ох. Разом з

тим при вирішенні великої кількості практичних задач достатньо знати

тільки деякі характерні риси закону розподілу. В теорії ймовірностей їх

називають числовими характеристиками випадкової величини X. Вони в

досить стислому вигляді характеризують той чи інший закон розподілу.

Властивості випадкової величини X характеризують параметри:

математичне сподівання, мода, медіана, дисперсія, середнє квадратичне

відхилення та стандарт. Більш узагальненими основними

характеристиками випадкових величин є моменти випадкової величини.

Математичне

сподівання

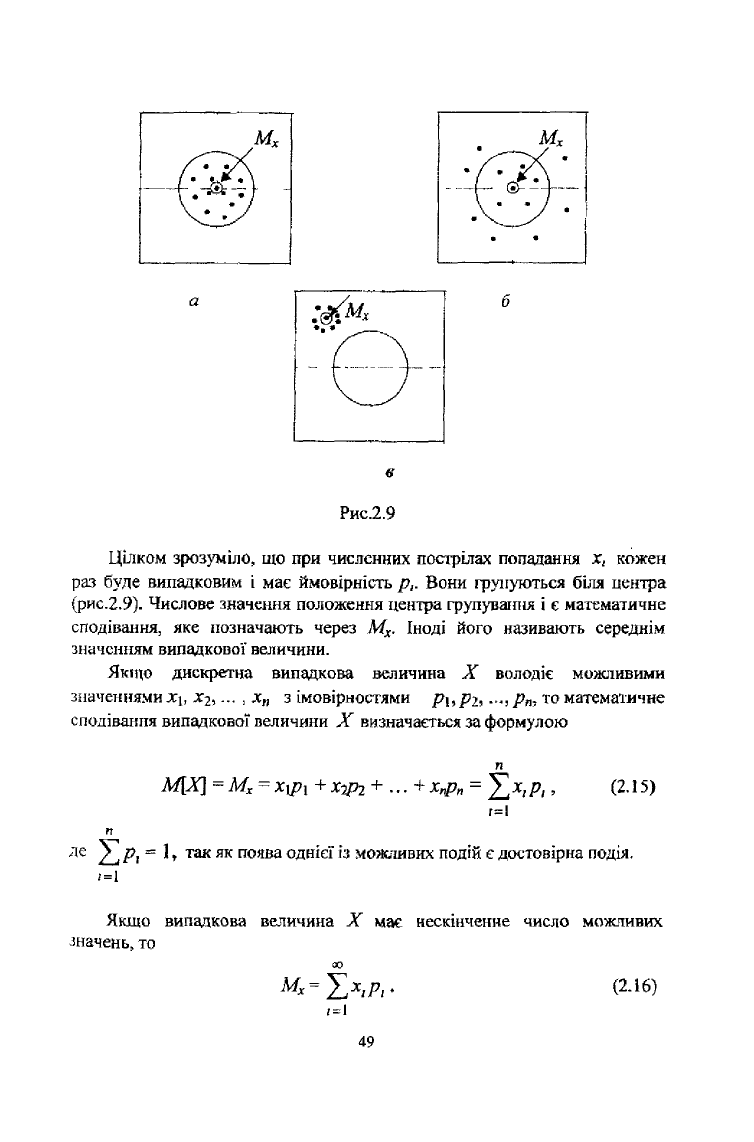
Розглянемо випадкову величину X - влучення в ціль при стрільбі по

мішені (рис.2.9).

Рис.2.9

Цілком зрозуміло, що при численних пострілах попадання х, кожен

раз буде випадковим і має ймовірність р,. Вони групуються біля центра

(рис.2.9). Числове значення положення центра групування і є математичне

сподівання, яке позначають через М

. Іноді його називають середнім

значенням випадкової величини.

Якщо дискретна випадкова величина X володіє можливими

значеннями X;, х

,... , х„ з імовірностями р\,рг,• р„, то математичне

сподівання випадкової величини X визначається за формулою

ЩХ\=М

= хф

+хтр

+ ... +х

= , (2.15)

г=І

ле 1, так як поява однієї із можливих подій є достовірна подія.

г = 1

Якщо випадкова величина X має нескінченне число можливих

значень, то

=^х

гРі

. (2.16)

(=1

Математичним сподіванням випадкової величини X

називається сума добутку всіх можливих значень випадкової

величини на ймовірності цих значень.

Математичним сподіванням неперервної випадкової

величини X, можливі значення якої належать відрізку [а, в],

називають визначений інтеграл

= |хф(х)й£е, (2.17)

де ф(х) - щільність імовірності розподілу випадкової величини.

Математичне сподівання має ту ж розмірність, що і випадкова

величина, та має властивості:

1. Математичне сподівання постійної величини дорівнює величині

постійної, тобто

М(С) = С. (2.18)

2. Постійний множник можна виносити за знак математичного

сподівання

М(СХ) = СМ

. (2.19)

3. Математичне сподівання суми декількох випадкових величин

дорівнює сумі їх математичних сподівань

М(х+у+...+ к)=М

+ М

+ ... +М

. (2.20)

4. Математичне сподівання добутку декількох взаємно незалежних

випадкових величин дорівнює добутку їх математичних сподівань

М(х

•

у •... к) = М

•

Му-... М

. (2.21)

Математичне сподівання може бути як додатнім, так і від'ємним.

Відомо, що для повної групи подій = 1. Тоді формулу (2.15)

можна записати у вигляді

= . (2.22)

Іл

/=1

Таким чином, згідно з формулою (2.22) виявляється механічна

інтерпретація математичного сподівання. Воно буде абсцисою центру

тяжіння системи матеріальних точок.

Якщо ймовірності появи випадкових величин х, однакові, тобто

V і рг ~ ••· ~ рм· то Рі =—, а формула (2.15) матимевигляд

£ \т

N N

де X - середнє арифметичне значення випадкової величини.

Це означає, що математичне сподівання приблизно дорівнює,

середньому арифметичному значенню випадкової величини. Воно буде

тим точніше, чим більше буде проведено дослідів. Графічно положення

математичного сподівання показано нарис.2.9.

Приклад 1. Визначити математичне сподівання числа вимірів кута

при п 'яти прийомах, якщо випадкова величина х (число вимірів) задана

рядом розподілу:

х,

о | і 2 3

4 5

Р>

0,01

0,08

0,23 0.35 0,26

0,07

Розв'язання. За формулою (2.15) обчислюємо:

= 0 · 0,01 + І

0,08 +2

0,23 +3

•

0,35 +

+ 4

•

0,26 + 5

•

0,07 = 3 {прийоми).

Приклад 2. При польовому контролі топографічної зйомки

інструментально перевіряють планове та висотне положення пікетів.

Ймовірність появи бракованого пікета дорівнює р. Контроль закінчують

після виявлення першого бракованого пікета. Знайти ряд розподілу та

математичне сподівання числа випробувань.

Розв'язання. Якщо X - випадкове число випробувань, то

ймовірність появи і-ої події визначається за формулою (1,36). За

Умовами

задачі п = і, к = 1, а

Роді

ряд розподілу випадкової величини х при д - Г- р запишеться

аб.'іично