Войтенко C.П. Математична обробка геодезичних вимірів. Теорія похибок вимірів
Подождите немного. Документ загружается.


А»х= 0,191.
За формулою (5.41) статистика X = В
тах
4п =0.191 -/90 = 1,81,
За таблицями дод. 11 при д-~- І- р~ 0.05; ^ = 1.36. Оскіпьки X >
(1,81 > 1,36), то при заданій надійній імовірності відхиляється нульова
гіпотеза, тобто ряд вимірів не підпорядковується нормальному закону
розподілу.
В іншому випадку порівнюють Дпах з теоретичним значенням
яке визначається за таблицями дод. 10 із рівня значності д і кількості?
вимірів п. Нульова гіпотеза підтверджується коли
А» < О
ч
. (5.43)1
Для нашого прикладу при ц = 0,05 і п
=•
90 отримаємо О
ч
= 0,14. В
цьому випадку > Ц, (0,191 >0,14) і так само нульова гіпотеза
відхиляється.
З, Критерій х
1
(Пірсона)
І
В математичній статистиці його вважають найбільш строгим і
надійним критерієм погодження нульових гіпотез. Він забезпечу|
мінімальну ймовірність виникнення похибок 2-го роду. )
Розрахунки в критерії Пірсона аналогічні критерію Колмогорова І
пов'язані з групуванням нормованих похибок. Слід пам'ятати, що прЙ
групуванні похибок в кожному інтервалі їх повинно бути не менше п'ятц.
Тому крайні інтервали можна штучно об'єднувати (збільшувати). Число!
інтервалів повинно бути не менше чотирьох.
Критерієм перевірки нульової гіпотези є статистика і
2 -Ир.)
1
X „ » (5.44.
ЇҐ1 Хрі
де N =
[ V,
] - число всіх вимірів, р, - теоретичне значення ймовірносі
вибраних інтервалів вибирається із таблиць дод. 12 за граничним]
значеннями початкового /„ і кінцевого 4 інтервалу.
В критерії Пірсона доведено, що при нормальному розподілі похибсЙ
вимірів статистика %
2
має Х
2
-розподіл з числом ступенів вільної
Критична область для нульової гіпотези буде
(5-45]
Д
е
Хд ~ вибирається із таблиць дод. 9 за заданими д і г = к — З
к-
киїькість інтервалів.
142

Приклад 3. Виконаємо перевірку критерієм Пірсона на нормальність
розподілу статистичного ряду, приведеного в критерії Колмогорова. Ряд
використаємо без змін довжин і кількості інтервалів, оскіяьт V, > 5
Таблиця 5.3
Г~№
і інтер-
валу
Інте рвал
V,
Рі
Мр,
(у,-АЮ
2
Мр,
' 1
^ 2
-Зі
-2
6
0,0214
2
16
8,0
' 1
^ 2 -2 -2
12
0,135
12
0
0
3 -1
0
27 0.3413
31
16 0,5
3
0 +1 24
0,3413
31
49
1,6
5
+1
+2
15
0,1359 12
9
0,8
^ 6
+2
+3
6
0,0214
2 16
8
90
0,9972
90
=18,9
%
2
= 18,9. За таблицями дод. 9 при #
—
0,05 і г = к
—
3-6
—
3 = 3
2 2 2
~І
а
= 7,8. Оскільки % >%
я
08,9 > 7,8), то ряд вимірів не підкоряється
нормальному закону, тобто висунута нульова гіпотеза відхиляється так
само, як і в критерії Колмогорова.
З іншими критеріями перевірки можна ознайомитися в роботах
[8:9].
Запитання для самоперевірки
1. Що таке нульова гіпотеза?
2. Які похибки виникають при статистичній перевірці гіпотез?
3. Які нульові гіпотези ви знаєте?
4. Як визначити наявність в статистичному ряду систематичних
похибок?
5. Що таке критерій Аббе?
6. Як визначити граничну похибку?
7. Яку нульову гіпотезу перевіряють критерієм Греббса?
8. Які критерії використовують при визначенні рівноточності двох
рядів вимірів?
9. Коли застосовують ^критерій та критерій Романовського?
10. Як перевірити рівноточність Л-рядів вимірів (л > 2)?
11. Яку нульову гіпотезу перевіряють критеріями Колмогорова та
Пірсона?
12. Приведіть порядок обчислень в критеріях Колмогорова та Пірсона.
143

ГЛАВА III. ТЕОРІЯ ПОХИБОК ВИМІРІВ
РОЗДІЛ 6. ОСНОВНІ ПОНЯТТЯ
1
КРИТЕРІЇ ОЦІНКИ ТОЧНОСТІ
ВИМІРІВ
§ 1. Предмет, задачі і
класифікація
похибок вимірів
Навколишнє середовище та явища, що в ньому виникають, «а
пізнаємо шляхом випробувань, дослідів, експериментів. При цьом'
виконується великий обсяг вимірів. Інформація, що міститься
п
результатах вимірів має велику наукову і практичну цінність. Мснделє*
говорив: "Наука починається там, де починають виміряти".
Виміри відіграють надзвичайно велику роль в різних галузях наую
техніки і виробництва. Вони є основою при вивченні форми і розмірі
Землі, її поверхні; при вишукуваннях, проектуванні, зведенні і ексшіуата|
інженерних споруд, при проведенні фундаментальних досліджень і т.д. А
Так при зведенні інженерних споруд за допомогою вимір
витримують їх точні геометричні параметри конструкції: висоту, довжин;
ширину, вертикальність елементів і забезпечують їх просторої
положення згідно з проектом споруди.
Вимір - це порівнювання шуканої величини з величино^
прийнятою за одиницю виміру. ц
Л
Ь = п1
0
+ г, (64
де
—
шукана величина; 1
0
- одиниця виміру; п — число повія
одиниць виміру; г - залишок (розмір неповної одиниці виміру). і
Геометричну схему вимірювання довжини і. показано нарис. 6.1
і = пі,, + г
/ " л
І Ь 1 Ь 1 1 ^ 1 - 1
Рис. 6.1
Залежно від призначення, вимірювання виконують з більшою
меншою точністю. Тому виникає необхідність в отриманні числС
характеристик розміру і точності виміряних фізичних величин. Пракі
показує, що безпомилкових вимірів не буває.
144

ФЬичною величиною називають властивість загальну в
якісному відношенні для багатьох об'єктів та індивідуальну
(різну) в кількісному відношенні для кожного фізичного об 'єкта.
В геодезії основними фізичними величинами є довжина та кут. Разом
з тим вимірюють площу, масу, температуру, тиск, час і інші фізичні
величини.
Довжина може бути розміщена в горизонтальній, вертикальній або
нахиленій площинах.
Кут - це поворот між двома положеннями рухомого променя, що
виходить із однієї вершини.
Одиниця виміру має відповідну назву, а тому і результат виміру є
найменованим числом.
Виміри виражають в Міжнародній системі одиниць СІ (або 57'). За
одиницю довжини прийнято один метр. Еталон довжини 1 метра
визначають через довжину електромагнітної хвилі, що проходить за
1/299792458 частку секунди в вакуумі.
За одиницю плоского кута приймають радіан. Це кут між двома
радіусами, що опирається на дугу, яка дорівнює радіусу Я.
Допустимими одиницями кута поряд з радіаном є градуси (°),
мінутиС ) і секунди("). При цьому 1 рад= 57,°3 = 3438' = 206265".
В природі існує істинне значення фізичних величин, яке для нас
невідоме. За результатами вимірів ми отримуємо дійсне значення
величини, яке, залежно від точності вимірів, може бути більш або менш
наближене до істинного.
Виміри виконують при певному "комплексі умов" (КУ). До
комплексу умов в геодезії відносять: а) об'єкт (що вимірюють), 2) суб'єкт
(хто вимірює), 3) прилад (чим вимірюють), 4) метод (як вимірюють),
5) середовище (де вимірюють).
Причини виникнення похибок вимірів прямо залежать від зміни
"комплексу умов". Вибір найкращих умов вимірів може призвести до
підвищення точності вимірів і навпаки - до її пониження. Окремі складові
комплексу умов можна змінювати залежно від необхідної точності
вимірів. Але знати їх абсолютно точно або досягта їх повної незмінності
практично неможливо.
В теорії похибок вимірів вивчають причини виникнення і закони
розподілу похибок вимірювань, властивості похибок І розробляють
методику спостережень. Це дозволяє забезпечити отримання результатів
вимірів з заданою точністю.
Теорія похибок вирішує дві найголовніші задачі:
1. Отримання ймовірного значення вимірюваної величини близького
до істинного.
2. Оцінку точності вимірювань.
145

За методикою виміри можуть бути:
- прямі або безпосередні, які отримують шлях^
безпосереднього порівнювання шуканої величини з одиниц^
виміру;
- непрямі або посередні, які отримують шляхом обчислень чер<
інші виміряні величини.
)
Наприклад Неприступну відстань через водні перешкоди отримуюй
шляхом побудови прямокутного трикутника, в якому вимірюють кут
базис (сторону).
За точністю виміри можуть бути:
• рівноточними, які виконані при практично незмінному комплею
умов;
• нерівноточними, які виконані при зміні комплексу умов. "
Практично рівноточність вимірів може бути визначена застосуванні
критеріїв перевірки (§ 1,розд.5). -
За кількістю виміри можуть бути:
• необхідними - кількість вимірів, яка необхідна для визначені
шуканої величини.
Наприклад', а) для виміру довжини лінії достатньо одного виміру,
для визначення недоступної відстані необхідно виміряти три величині
два кути і базис. \
• надлишковими - різниця між кількістю виконаних вимірів!
кількістю необхідних вимірів. ^
Наприклад. Якщо число всіх вимірів дорівнює п. необхідних виміріб
то число надлишкових вимірів г визначиться за формулою
г = п-к. (4
В практиці геодезичних вимірювань надлишкові виміри відіграй
надзвичайно важливу роль. Вони дозволяють вирішити задачі похи|
вимірів, визначити промахи в вимірах і обчисленнях, підвищити точК^
виміряних величин.
Якщо результат виміру буде х„ а істинне значення виміри
величини X, то різницю між ними називають істинною похибкою А, -
А, =х,-Х.
46

За походженням похибки вимірів поділяють на приладні, особисті,
зовнішні і методичні.
Приладні похибки обумовлені недосконалістю конструкцій
вимірювальних приладів, неточністю їх виготовлення.
Особисті похибки (суб'єктивні) викликані особистістю спостерігача,
Його станом в період роботи, недосконалістю органів відчуття тощо.
Зовнішні похибки виникають із-за зміни середовища в процесі
вимірювань.
Методичні похибки виникають при неповному врахуванні умов
вимірів та їх зміни.
Класифікація похибок вимірів. Виміри будуть доброякісними, коли
похибки вимірів не перевищують граничних величин. В противному разі їх
відносять до неправильних. Тому їх поділяють на:
1. Грубі помилки або промахи. В теорії похибок вимірів до них
відносять виміри, в процесі яких виникали промахи, або виміри, похибки
яких перевищують граничні похибки за умовами вимірів.
Грубі помилки можуть виникнути і в процесі обчислень. Із обчислень
повинні бути виключені результати, що мають грубі помилки.
2. Систематичні похибки. Такі, що входять до кожного результату
вимірів за строго визначеним законом. їх поділяють на постійні, що
кожен раз діють із однаковим знаком і величиною та перемінні, що
змінюють свою величину в процесі вимірів за строго визначеним
законом.
Наприклад, визначена поправка компарування до довжини рулетки
буде постійною при заданій температурі Однак із зміною температури
вона буде змінюватися пропорційно зміні температури і стане
перемінною.
Дія систематичних похибок досить значна, тому як правило, шляхом
досліджень їх визначають і методикою вимірювань зводять їх дію до
мінімуму.
3. Випадкові похибки. Повне врахування зміни комплексу умов
практично неможливо. Тому результати вимірів супроводжуються
випадковими похибками, обумовленими постійною зміною комплексу
Умов. Характер дії випадкових похибок можна визначити на основі
великої кількості вимірів. Дослідження характеру дії випадкових похибок
виконують статистичними методами (§ 1, розд.5). Звільнитись від дії
випадкових похибок неможливо, тому виявлені статистичні закономірності
Дозволяють лише зменшити їх вплив на результати вимірів.
В свою чергу випадкові похибки поділяють на істинні Д та ймовірні
У- Істинні похибки Д, визначають за формулою (6.3).
147

Ймовірні похибки V, визначають як різницю між результатом вий
х, і дійсним значенням X, отриману обчисленням за результаті
вимірів ^
У,=х,-Х. (6,
Систематичні і випадкові похибки діють одночасно. Так різниця і
дійсним і ісгинним значеннями виміряної величини &
систематичною похибкою X, тобто >
Х
=
Х-Х. і(
*
Тоді із різниці формул (6.3) та (6.4) отримаємо
Л-Г = Х-Х
=
Х. щ
Дослідженнями встановлено, що дія випадкових похибок має пс
властивості,
Властивості випадкових похибок. При незмінному комплексі умов |
випадкових похибок Л|, Аг, А„ однієї і тієї ж величини і
властивості:
1. Обмеженості - абсолютні значення випадкових похибок
перевищують заданої граничної величини ' і
і
|Д| <, Арр
2. Унімодальності - число N мінімальних за абсолютним значой
випадкових похибок в ряду вимірів значно більше кількості максималИ
похибок 1
|»ЛГ,
л
..
^шші Ріпах і
3. Симетричності - в статистичному ряду кількість мінуо
похибок приблизно дорівнює кількості плюсових похибок
А(-Д) ~ Щ+ьу ^
4. Компенсації
—
гранйчне значення середнього арифметично^
суми значень випадкових похибок при їх безмежному зроо|
наближається до нуля, тобто >
".і
Ііт — » 0. (|
п-*
ОО
п >·
ч
Властивості випадкових похибок лежать в основі розробки меі
математичної обробки вимірів.
148

§ 2. Розподіл імовірностей випадкових похибок
Результати вимірів є випадковими оскільки передбачити їх величину
неможливо. Тоді і їх похибки будуть випадковими і для них можна вказати
дише межу, в яких вони змінюються згідно з першою властивістю (§ 1).
Неперервні випадкові похибки можна характеризувати законом
розподілу, як об'єктивно існуючим зв'язком між випадковими величинами
і їх імовірностями.
При багаторазових випробуваннях закон розподілу ряду істинних
випадкових похибок можна характеризувати функціями:
1. Інтегральною функцією розподілу
F (Д) = />(£Х< А). (ОС < Л). (6.11)
2. Функцією щільності
ф(д) = іїтгі — -, (6.12)
s->o 5
де 8 ~ приріст випадкової похибки А.
Звернемося до постулат)' Гаусса, згідно з яким найбільш імовірним
значенням шуканої величини є середнє арифметичне із результатів
повторних вимірювань. Скористаємося теоремою:
Якщо випадкові похибки відповідають постулату Гаусса, то
законом розподілу випадкових похибок буде нормальний закон. В методі
максимальної правдоподібності Фішера (ММП, § 3, розд.4) також
доведено, що для нормального закону розподілу випадкових величин
оцінкою параметра а е середнє арифметичне (формула4.18).
Функція щільності нормального розподілу випадкових похибок
визначиться за формулою
_ LA
2
'
ф(Д)=
2
°
2
- (6.13)
мітоз
_ Д
Для нормованих похибок t, - — отримаємо
1 2
1 -
2
'
(6Л4)
оскільки ст(0 = 1 , a M(t) = 0.
149
-д
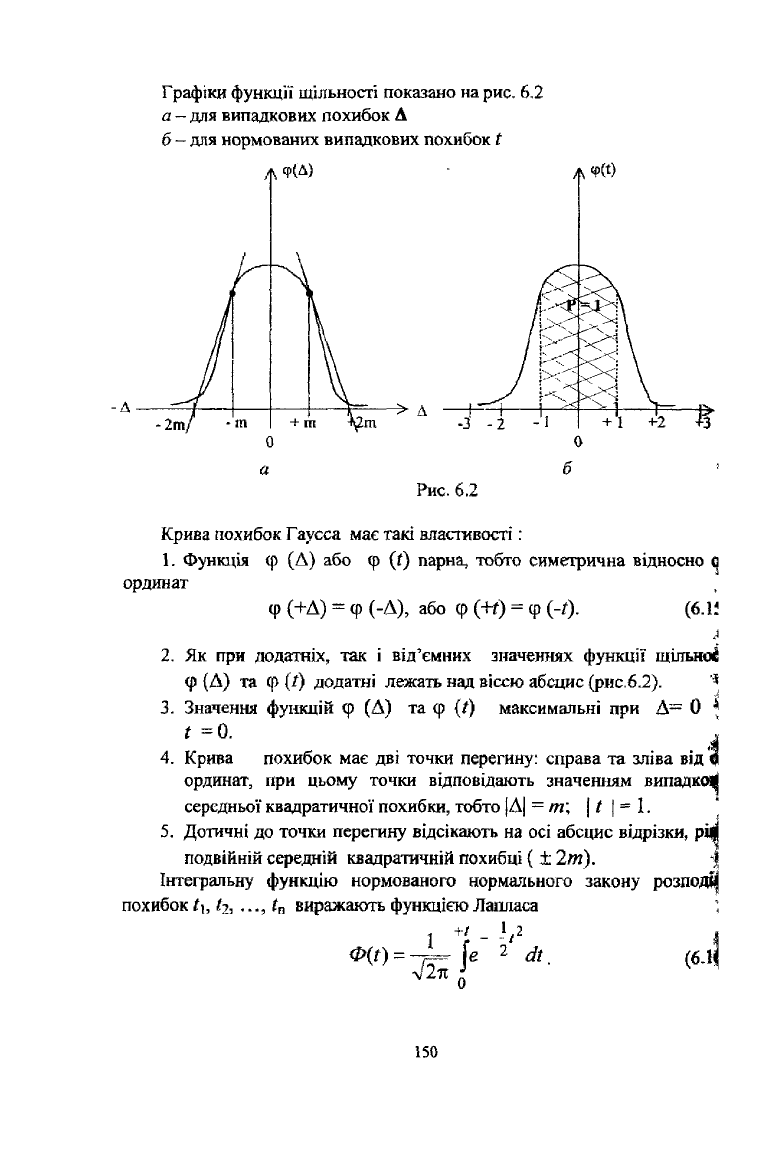
Графіки функції щільності показано на рис. 6.2
а - для випадкових похибок Д
6 - для нормованих випадкових похибок ґ
А Ф(Л)
Рис. 6.2
Крива похибок Гаусса має такі властивості:
1. Функція (р (Д) або ф (() парна, тобто симетрична відносно <]
ординат
ф (+Д) = ф (-Д), або ф (+0 = ф (-/). (6.1І
2. Як при додатніх, так і від'ємних значеннях функції щільної
ф (Л) та ф (/) додатні лежать над віссю абсцис (рис.6.2).
3. Значення функцій ф (Д) та ф {/) максимальні при Д— 0 *
і =0.
4. Крива похибок має дві точки перегину: справа та зліва від
ординат, при цьому точки відповідають значенням випадко^
середньої квадратичної похибки, тобто |Л| = т\ | ї \ = 1.
5. Дотичні до точки перегину відсікають на осі абсцис відрізки, р:
подвійній середній квадратичній похибці ( ± 2т).
Інтегральну функцію нормованого нормального закону розподЦ
похибок І),
1.2·.
·•;(, .щ виражають функцією Лапласа
- \е~ 2 сії
4іп
<«-Ч
150

Значення функції (6.16) табульовані і приведені в таблиці дод. 1.
За таблицею можна по заданій надійній імовірності визначати
інтервал, в якому знаходяться нормовані похибки від — Г до + / і
навпаки, задавшись інтервалом ±
1
визначати ймовірність їх появи р.
± А = т,
або -Іт<А < + Ш, -і (6.17)
де т - середня квадратична похибка вимірів.
§3. Числові характеристики рівноточних вимірів
Рівноточними, називають виміри, дисперсії яких рівні між собою,
2 2
тобто СУ. =сг.·. Тому рівноточні виміри можна виразити статистичним
рядом
Х
Ь
Х
2
,...,Х„, (о,
2
=сф. (6.18)
Якщо невідоме істинне значення вимірюваної величини X, то
необхідно знайти значення близьке до істинного. Його називають
дійсним, або ймовірним значенням виміряної величини. Воно може бути
прийнятим, коли точність вимірів задовольняє поставленим вимогам, або
- відхилене. Тому постає задача обчислення за результатами вимірів
показників як розміру шуканої величини, так і її точності. їх називають
числовими характеристиками. В теорії похибок вимірів до числових
характеристик відносять:
1. Середнє арифметичне
Використаємо ряд вимірів (6.18). Якщо відоме істинне значення
вимірюваної величини X, то визначимо ряд істинних похибок
А/ ~
х
і ~ X '•> 0" = 1") (6.19)
Складемо їх і поділимо на п
п п
За чегвертою властивістю компенсації випадкових похибок Д ліва
частина формули (6.20) наближається до нуля при и —> да. Позначимо
середнє арифметичне
Х = (6.21)
п
151
