Войтенко C.П. Математична обробка геодезичних вимірів. Теорія похибок вимірів

Подождите немного. Документ загружается.

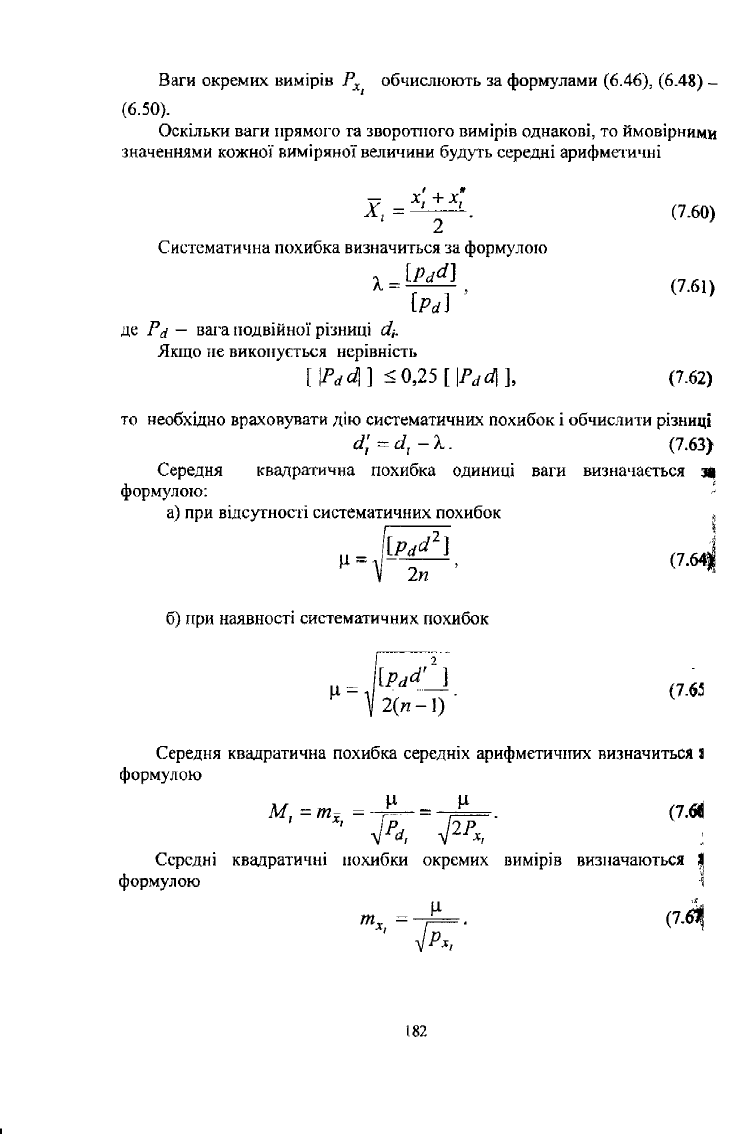
Ваги окремих вимірів Р

обчислюють за формулами (6.46), (6.48) -

(6.50).

Оскільки ваги прямого та зворотного вимірів однакові, то ймовірними

значеннями кожної виміряної величини будуть середні арифметичні

Систематична похибка визначиться за формулою

У _ \-Pdd]

к = - - , (7.61)

ЇА*]

де Реї

—

вага подвійної різниці (І).

Якщо не виконується нерівність

£0,25[|Л,4], (7.62)

то необхідно враховувати дію систематичних похибок і обчислити різниці

(1\

—

с!

;

—

X. (7.63)

Середня квадратична похибка одиниці ваги визначається за

формулою: "

а) при відсутності систематичних похибок ,

б) при наявності систематичних похибок

ц = (7.65

№-1)

Середня квадратична похибка середніх арифметичних визначиться

формулою

М,=т-

(7 М

' Л ^ :

Середні квадратичні похибки окремих вимірів визначаються |

формулою 1

**,=-г=· (

182

За вимогами інтервал для істинного значення кожного із вимірів може

бути визначений за формулою (7.38). При необхідності визначають

інтервал для дисперсії або стандарту середнього арифметичного та

окремих вимірів за формулами (7.15) - (7.20). Обчислюють відносні

похибки.

Приклад. Лінії теодолітного ходу виміряні рулеткою в прямому і

зворотному напрямках Виконати обробку вимірів 3 оцінкою точності

при надійній імовірності р = 0,95.

Розв'язання. Оскільки вимірювання ліній виконано в прямому та

зворотному напрямках однією рулеткою при практично однакових

2 2

умовах, та дотримується рівність дисперсій = а* . Разом з тим

І»

довжини ліній різні, тому сг

Ф а^ та ст, Ф а

, а виміри

вважаються подвійними нерівноточними

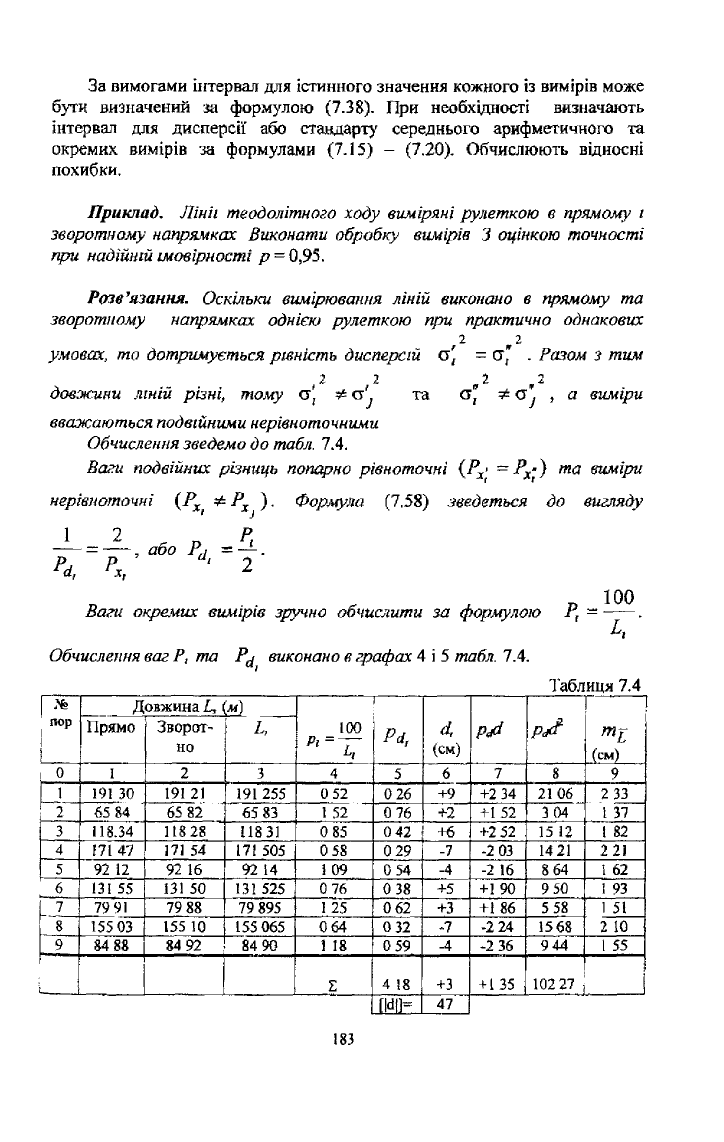
Обчислення зведемо до табл. 7.4.

Ваги подвійних різниць попарно рівноточні {Р

· = Р

·) та виміри

нерівиоточні {Р

х>

фР

^). Формула (7.58) зведеться до вигляду

12 Р,

= , або Р, = -

Р<і, Рх, ' 2

Г, 100

Ваги окремих вимірів зручно обчислити за формулою Р, = .

Обчислення ваг Р, та Р^ виконано в графах 4 і 5 табл. 7.4.

Таблиця 7.4

JÉ

Довжина L, (jw)

пор

Прямо Зворот-

но

100

Рі=

1Г

Рч,

(cm)

Pdd

Pd£

Гем)

І 2 3 4

8 1 9

191

191255

0 52

0 26

+9 +2 34

06 2 33

65 84 65 82

83 1 52 0 76 +2

52 3 04

1 37

118.34 11828

11831 0 85 0 42 +6

+2 52

15 12 1 82

171

171 54

17! 505

0 58

0 29

-7 -2 03

21 221

92 12

92 16

92 14

0 54

-4 -2 16

64 1 62

131

525

0 76

0 38

9 50 1 93

79 91

895

25 0 62 +3 +1 86

5 58

1 51

155

155 10

155

065 064 0

-7

-2 24

68 2 10

84 88 84 92 84 90 1 18

0 59

-4 -2 36 944 1 55

4 !8

+3 +

102

№

183

Систематична похибка складе

Ш 4,18

Визначимо контроль відсутності систематичних похибок

<0,25 [Н] 1,35 < 0,25-47 (1,35 < 11,75),

тому критерій виконується.

Середні арифметичні Ц із результатів вимірів ліній обчислені в

графі 3, табп.ІЛ.

Середня квадратична похибка одиниці ваги буде

•

' иі,і

„ ,, „

СМ.

IP^J 102,27

\ In V 1.8

Середні квадратичні похибки вимірювання окремих вимірів будуть

Середні квадратичні похибки середніх арифметичних

Результати обчислень приведені в графі 9. При р — 0,95 і

п — 1 = 8 за таблицями розподілу Стьюдента (дод. 3) параметр

= 2,5. Тоді граничні похибки для мінімальної та максимальної довжини

лінії будуть

для і

Агр

= ± і»М= ± 2,5

•

1,37 = ± 3,42 см,

дляЬі Дгр ~ + 2,5 - 2,33 = ± 5,82 см.

Відносні похибки складуть

гр __ 3,42 „11.

Г, L

6583 1925 2000

1 _ A

_ 5,82 _ 1 ^ 1

Ц 19125 3286 2000

Як показують розрахунки, короткі за розміром лінії виміряні з

точністю нижче від вимог інструкції.

184

Б. В практиці геодезичних вимірювань може бути випадок, коли всі

г 2 2

результати між собою нерівноточні, тобто

(Ту , а" Ф сг* та

2 2

А І ФІт, .

В формулі (7.58) р

Хі

., тоді

1 _Рх, +РІ

Рі, р'х, Рх,

Вага подвійних різниць обчислюється за формулою

/ я

Р^-^Г- (7-68)

Рх,

Середні арифметичні обчислюють за формулою

- Рх

'і + Рх

X, ---- '. (7.69)

Рх,

Далі розрахунки точності виконують за формулами (7.61) - (7.65).

Середні квадратичні похибки арифметичних середніх обчислюють за

формулою

, / , . (7.70)

Необхідно вказати, що такі випадки в практиці геодезичних

вимірювань зустрічаються дуже рідко.

§ 4. Оцінка точності

функцій виміряних величин

В практичній діяльності для вимірювання шуканих величин часто

застосовують посередні методи. При цьому шукана величина ¥

визначається шляхом обчислень по виміряних величинах Х\, Х

, ..., Х„-

Шукану величину У називають функцією, а виміряні величини

X, - аргументами, тоді

¥=/(ХиХі ...,Х„), (7.71)

де У, Х

Хь Х„~ істинні значення функції та її аргументів.

Зрозуміло, що виміри виконуються з похибками, тому і функція буде

обтяжена похибкою. В результаті повторних вимірювань аргументів ХІ

можна визначити їх точність, або їх точність визначається методикою

вимірювань на основі інструкцій і т.і.

185

Похибка функції буде залежати від похибок її аргументів. Якщо

виміряно аргументи Х\,

· ••,

х„ , то шляхом обчислень можна визначити

функцію

у =/(х

Хг -,х

), (7.72)

де Х\, Хь ..., х

- виміряні величини з середніми квадратичними

похибками т

Хі

,т

Х2

, ..., т

Хп

- Припустимо, що нам відомі істинні

похибки вимірів Д[, Д2, ..., Л„. Очевидно і функція отримає істинний

приріст Ау. Функція (7.72) зведеться до вигляду

у + Ау=/(х, + Д,, х

+ Дь-. х» +ДД (7-73)

Функція (7.71) може мати нелінійний характер, а тому приведемо її до

лінійного виду.

Розкладемо функцію (7.71) в ряд Тейлора і отримаємо

У = у + Ау =/(*і, Хг-, *„) +

,Г ^

дх.

(Х!-Х) +

де

1/0

(х

-Х

) + ...+

(7.74)

часткові похідні від функції по перемінних наближених

значеннях аргументів;

х, -X,

—

А, ~ істинні похибки аргументів функції;

К - величини другого та вищих порядків малості і в подальших

розрахунках може бути прийнятою за нуль, тобто Я ~0.

Визначимо приріст функції Ду, для чого від рівняння (7.72)

віднімемо рівняння (7.74) і отримаємо

У - У

- Ау = /(Х

, X») -/(Х\,Х2,...,Х„)·

^і/о

5/1

А„

або

дх

2о

дх.

А„.

(7.75)

і2о

Для оцінки точності функцій застосуємо метод повторних вимірювань •

аргументів. Тобто припустимо, що аргументи функції виміряні л-разів і

при відомих істинних похибках аргументів обчислено таку ж кількість

похибок функції, тобто

186

(Сі

ж.

і=(1,и). (7.76)

Зведемо їх до квадрата, складемо і поділимо на п. Отримаємо

дх.

' ' о

ґ ^ \

- +... +

дх

)

44]

Згідно з формулою (6.24) маємо

ґ _„ Л

ІО

[А*

]

п п

(1Л)

(7.78)

п ' п

Із кореляційного аналізу за формулою (4.48) можна визначити

коефіцієнт кореляції за формулою

[А, А,]

г„= -. (7.79)

Тоді дисперсія функц ії за формулою (7.77) зведеться до вигляду ~1

Ц -ї + *

т\

удхп; о

ті +

2У І І

х,

Х]

··

(7.80)

або т.

дх.

¥) {¥

дх,

у ; ^

(7.81)

де г

- коефіцієнт кореляції, який виражає залежність між аргументами х,

та*,.

187

•Г

Формули (7.80) та (7.81) виражають дисперсію функції, тобто Ц;

точність залежно від виду функції і точності залежних між собою

аргументів.

Практично досить важко і економічно невигідно визначать

коефіцієнти кореляції. Тоді умовно приймають їх незалежними, «

коефіцієнт кореляції Гу «0. '/Ь

Для незалежних аргументів дисперсія функції буде •

т,

Ч^і У о

к.

/о

+... +

*« у

< , (7.

де т

, ті, т

, ..., т„ - середні квадратичні похибки функції та І

аргументів.

В узагальненому вигляді середню квадратичну похибку функції

незалежних аргументів виражають формулою

т.

-Ш*

т,

(7.83

В теорії похибок вимірів для визначення дисперсії функції (7.7}

застосовують правило:

1. Диференціюють функцію (7.72)

, ф , 5/ , дГ ,

дх] дхі

дх„

{ЇМ

2. В отриманій формулі (7.84) зводять до квадрату кожен член раза

із своїм знаком

л2 ,

ОХ]

+ с

дх

ах„

. (7.:

3. В формулі (7.85) замінюють

Ф"

1; л

\ =

х,, -> ,

тобто

ш.

дх

Хі

З/

дх

Хі

+...+

К.

\дх„;

2 І

" і

Як бачимо, отримана формула повністю співпадає з формулою (7.85

Для зручності середні квадратичні похибки позначаємо нумерації

аргументів : т

- , т

Х2

= т

і т.д. \

188

Приклади·. 1 Маємо функцію у = кх

Розв'язання. сіу = ксіх, сіу

—

сіх}

2 2 2

=к т

, або т

= кг,

2 Маємо функцію у = х

±х

±...±Х„

(7 86)

(7.87)

(7 88)

Розв'язання. сіу

•=

сіх

± сіх

±.. ± сіх

=(Л,)

(±Л

)

± -(±сіх

)

= т

+ Ш

+ ЇП-

Л/а&мо

функцію у = ± к

±... ±к

Розв'язання. сіу - к

сіх

]

± к

сіх

±... ± к

ск

;

сіу

=(к

ск

)

(±к

ск

)

±,..(±к

сЬе

)

т; - кут

. + кЬп

^ і , , +*>:

4. Маємо функцію г = х у

Розв'язання, а) ~ усіх + хсіу

-{усіх)

+ (хсіу)\

2 2 2 2 2

= у т

+ х т

2 2.

б ) їж = Іпх + Іпу;

—аг = ах + —ау,

2 X у

<Ь

-сіх

(7 89)

(790)

(7.91)

(7.92)

(7.93)

1 ,

+ -сіу

+ШІ

2 2 2

хху

(7.94)

2 2 2

Якщо в отриманій формулі замінити 2 —х у , то отримаємо

2 2 2 2 2

= у т

+ х піу,

що приводить до попередньої формули (7 93).

189

5 Маємо функцію z =

—

(7 95)

Розв'язання Inz = Іпх

—

Іпу

dx-~dy·, f ~dz 1 = ( --cfe ] f -—dy | ,

z x j wywA^j

1 1 2

m. m~, m

або ~2=^t

2 (7 96)

Z X у

Як бачимо, дисперсія функції добутку (7 94) співпадає з дисперсією

функції ділення величин х та у (7.96)

6 Маємо функцію перевищення h = S

•

tg v

Розв'язання. Визначити дисперсію функції можна без проміжних

викладок Для цього пам'ятаємо а) всі члени в формулі дисперсії функції

будуть позитивними, б) похідні від вихідної функції зводяться до

квадрата

множаться на дисперсії відповідних перемінних Тоді

2 2 2

' 7

Щ = tg v m

+ — m

COS V

Оскільки m

має лінійну розмірність, m

— кутову, а шукана

величина mh

—

лінійну, то зводимо другий член формули до лінійного виду

Середня квадратична похибка визначення перевищення визначиться

за формулою

Г~2

2 S

ті

= tg v m

+ f

V cos v p

7 Площа прямокутного поля визначена вимірюванням сторін

а = 150 м і Ь

••

210 з середніми квадратичними похибками т

= 3 см,

ть = 5 см Обчислити похибку площі ділянки

Розв'язання, Маємо функцію S = a b

Тоді m

- b т

+ а

або m

= 7(210)

(0,03)

+ (150)

(0,05)

= ,/39,69 + 56,25 =

/95,94 =9,8м

190

Визначення ваги функції

Вага функції є мірою відносної точності і її можна збільшувати або

зменшувати в певну кількість разів С = 10

±л

Розглянемо дисперсію функції (7,82) для незалежних аргументів.

с „ . . . 2 1

л,

Відомо, що р, = — . Тоді в формулі (7.82) можна замінити т

т;

2 С

= , отримаємо

— +

у >0^1

Щ С

дх

Х2

Щ ^ (7.97)

Це і є формула оберненої ваги функції, після обчислення якої можна

перейти до ваги функції. Коефіцієнт С вибирають так, щоб значення ваги

було близьке до одиниці для зручності її використання.

Для визначення ваги функції в теорії похибок вимірів користуються

правилом:

1. Визначають дисперсію функції.

2 2 2

2. Дисперсії всіх перемінних т

, т

, ..., і т.д. замінюють на

обернені ваги відповідно

с с с

* х

Приклад. Перевищення між точками визначено способом

тригонометричного нівелювання за формулою И = зіп 2у .

Визначити вагу перевищення Рь при Б - 100 м; V = 5°30', т

= 0,5 м;

т„= 0',5.

Розв'язання. За умовами вимірів аргументи функції 8 і V

незалежні. Використаємо правило визначення дисперсії функції і

отримаємо

2 1 - 2~ 2 5

С08

2у 2

=-зіп 2у-/и.+ ;

4 Р

191