Волкова Е.С. Сборник домашних контрольных работ
Подождите немного. Документ загружается.

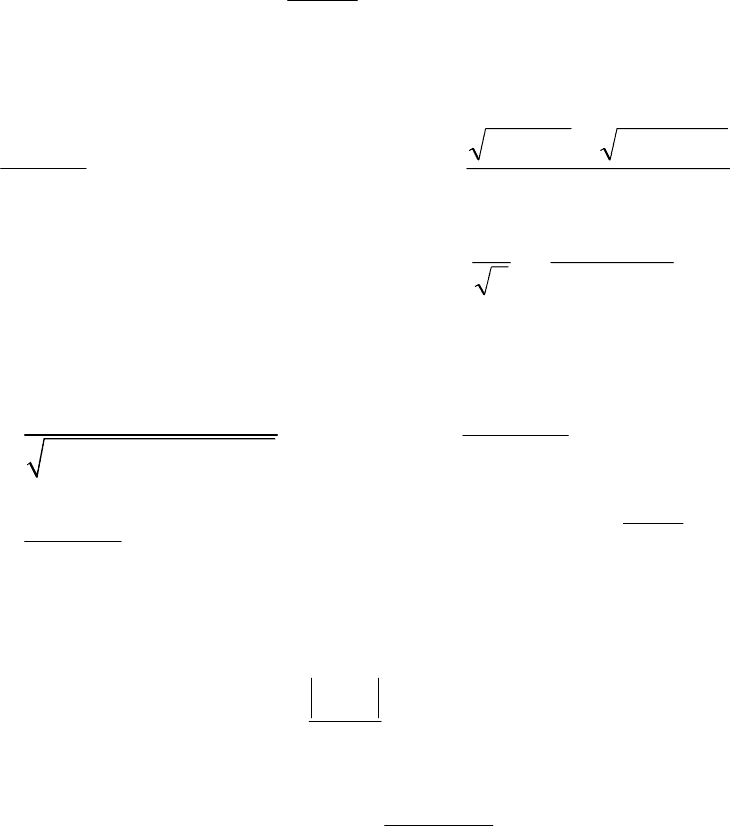
30
ВАРИАНТ 24
1. Пользуясь определением предела последовательности, докажите, что
2
53
61
lim =
+
+
∞→
n
n
n
.
2. Найти предел числовой последовательности:
а)
n
n
n
n
n
+
+
+
∞→
1
2
5
5
lim ; б)
5
1499
lim
22
nnnn
n
−−+
∞→
;
в)
(
)
)5ln()2ln(lim
222
+−+
∞→
nnn
n
; г)
+
++
∞→
3
12
sin
1
lim
2
n
nn
n
n
.
3. Найти предел функции:
а)
2
2
10
2
lim
( 1)( 11 10)
x
xx
xx x
→− +
−−
+++
; б)
xx
x
x
sin
5cos1
lim
0
−
→
;
в)
−
+
+
∞+→
x
x
xx
x
2
23
1
3
lim ; г)
()
4
2
sin(3 )
0
lim 1 2sin (4 )
x
x
x
x
→
−
.
4. Найти точки разрыва функции и определить характер этих точек
1
1
2
3
−
−
=
x
x
y
.
5. Найти асимптоты графика функции
2
1
2
+
++
=
x
xx
y
.
6
*
. Доказать, что уравнение
32
230
x
xx−+ +−=
имеет хотя бы один действительный корень, и найти его приближенное
значение с точностью до сотых (решение обосновать).
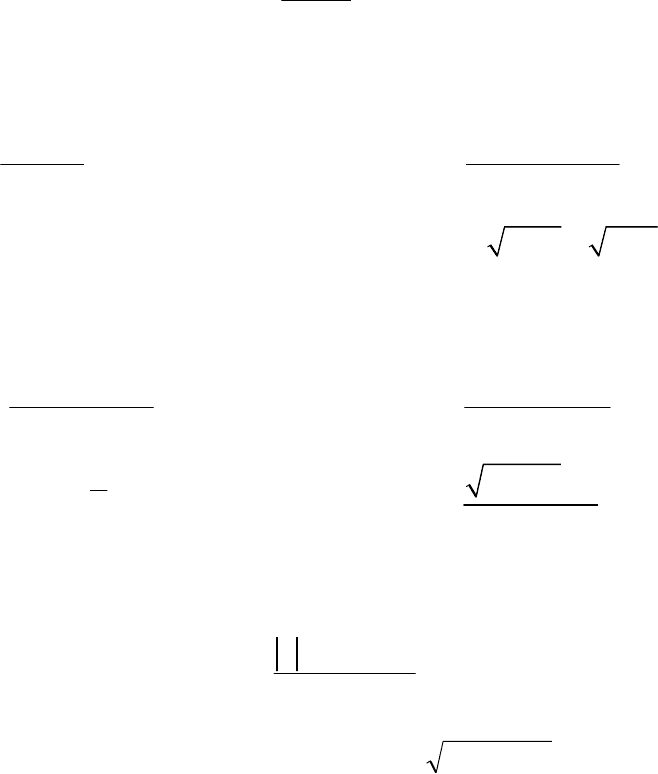
31
ВАРИАНТ 25
1. Пользуясь определением предела последовательности, докажите, что
13
lim 1
35
n
n
n
→∞
−
=
−
+
.
2. Найти предел числовой последовательности:
а)
nn
nn
n
73
52
lim
+
+
∞→
; б)
n
nn
n
+
+
+
−+
∞→
...21
3124
lim
2
;
в)
(
)
lim(2 1) ln( 16) ln( 2)
n
nn n
→∞
++−+; г)
(
)
(
)
lim 2 1 cos
n
nn n
→∞
+− + .
3. Найти предел функции:
а)
32
2
4
516
lim
16
x
xx
x
→−
+−
−
; б)
()sin
lim
1cos3
x
x
x
x
π
π
→
−
⋅
+
;
в)
()
3
3
3
0
51lim
x
x
x−
→
; г)
2
3
0
12 1
lim
tg5
x
x
x
x
→
+
−
⋅
.
4. Найти точки разрыва функции и определить характер этих точек
2
sin( 1)xx
y
x
x
⋅
−
=
−
.
5. Найти асимптоты графика функции
1
2
++−= xxxy .
6
*
. Доказать, что уравнение
02515237
23
=
−
+
+
x
x
x
имеет хотя бы один действительный корень, и найти его приближенное
значение с точностью до сотых (решение обосновать).
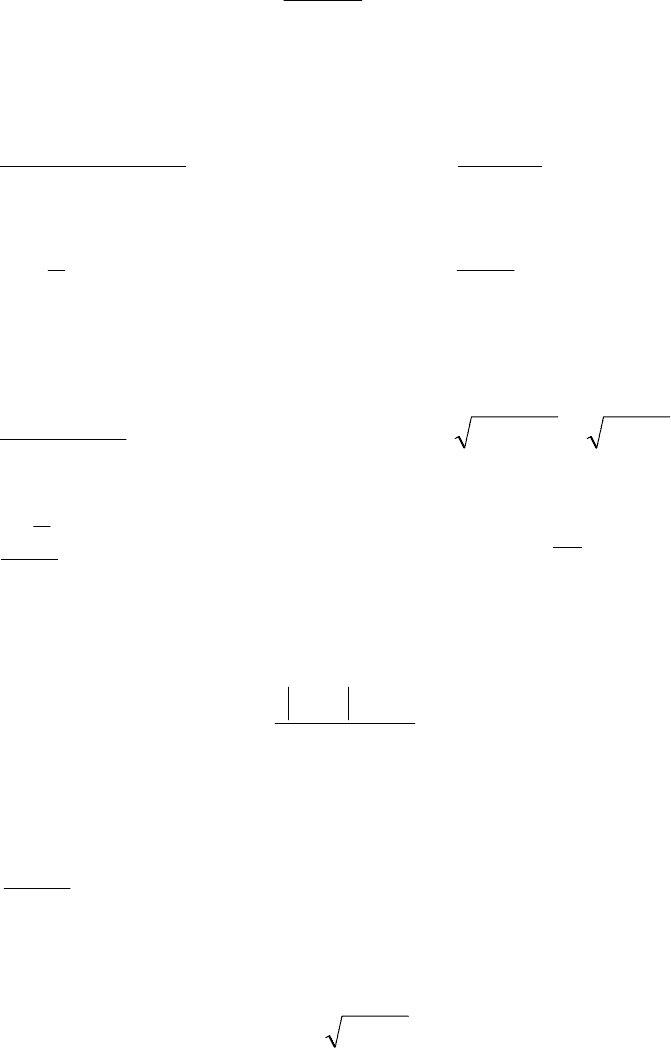
32
ВАРИАНТ 26
1. Пользуясь определением предела последовательности, докажите, что
2
54
110
lim =
+
−
∞→
n
n
n
.
2. Найти предел числовой последовательности:
а)
7
34
)133(
)32()1(
lim
+
+−
∞→
n
nn
n
; б)
−
−
+
∞→
n
n
n
n
5
2
35
lim
2
;
в)
⋅
∞→
n
n
n
sin
1
sinlim ; г)
13
9
lim
+
∞→
+
n
n
n
n
.
3. Найти предел функции:
а)
34
23
lim
5
4
1
+−
+−
→
xx
xx
x
; б)
(
)
12lim
22
+−+
∞→
xxx
x
;
в)
ex
e
x
ex
−
→
ln
lim ; г)
()
x
x
x
7
10
0
sin1lim
−
→
+ .
4. Найти и исследовать точки разрыва функции
xxx
xx
y
2
sin2
23
−−
−
= .
5. Найти асимптоты графика функции, если:
а)
x
x
y
1
2
+
= ; б)
arctgyx x=+
.
6
*
. Доказать, что уравнение
0sin12)1(
222
2
=+−⋅+
++
xxx
xx
имеет хотя бы один действительный корень, и найти его приближенное
значение с точностью до сотых (решение обосновать).
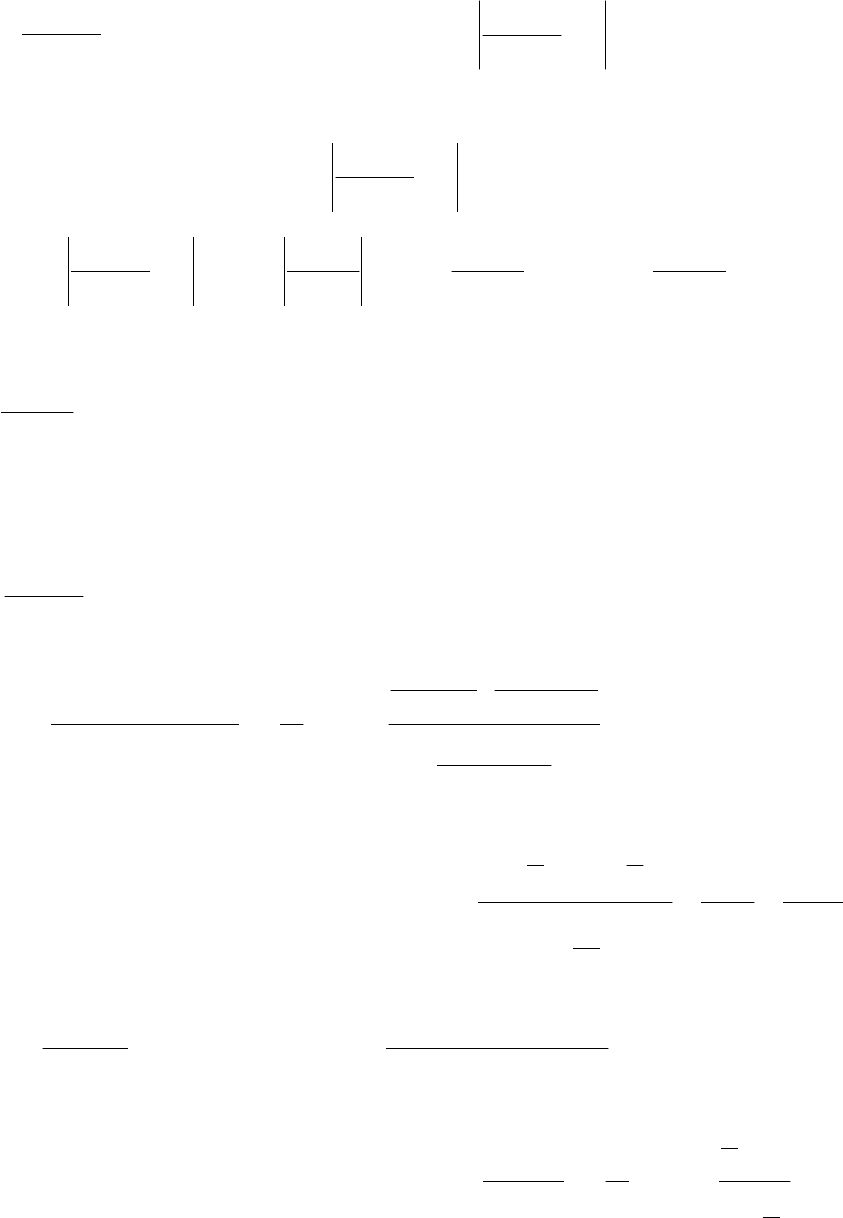
33
Решение варианта 26
1
. 2
54
110
lim =
+
−
∞→
n
n
n
⇔
εεε
<−
+
−
⇒>∀∃>∀ 2
54
110
:)(0
n
n
NnN
.
Преобразуем неравенство
ε
<−
+
−
2
54
110
n
n
. (1)
ε
<−
+
−
2
54
110
n
n
⇔
ε
<
+
−
n54
9
⇔
ε
<
+
n54
9
⇔
ε
ε
5
49 −
>
n .
Пусть
N
– любое натуральное число, удовлетворяющее условию
ε
ε
5
49 −
>
N . Ясно, что такое число
N
существует, для каждого положи-
тельного числа
ε
. Тогда для любого
N
n > будет иметь место неравенство
(1). Следовательно, число 2 является пределом последовательности
n
n
x
n
54
110
+
−
= .
2. а) =
+
+
⋅
−
=
∞
∞
=
+
+−
∞→∞→
7
7
3
3
4
4
7
34
)133(
)32()1(
lim
)133(
)32()1(
lim
n
n
n
n
n
n
n
nn
nn
2187
8
3
21
13
3
3
2
1
1
lim
7
3
7
34
=
⋅
=
+
+
−
=
→∞
n
nn
n
.
б)
()
=
−
+−+
=∞−∞=
−
−
+
∞→∞→
2
10535
lim5
2
35
lim
222
n
nnn
n
n
n
nn
10
2
1
10
3
lim
2
103
lim =
−
+
=
∞
∞
=
−
+
=
∞→∞→
n
n
n
n
nn
.
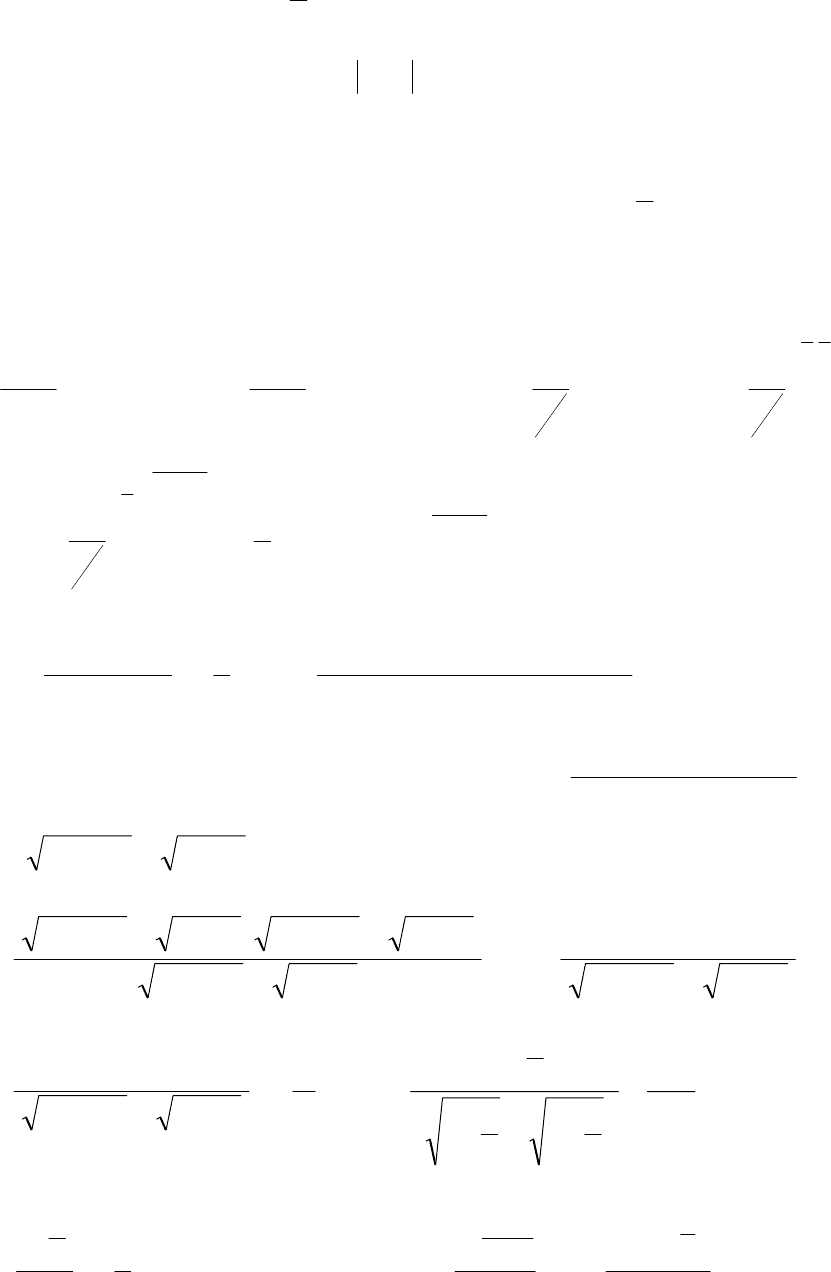
34
в) Последовательность
n
1
sin является бесконечно малой. Последова-
тельность
{}
nsin – ограниченная
(
)
nn
∀
≤
,1sin . Произведение бесконечно
малой последовательности и ограниченной последовательности является
бесконечно малой последовательностью, значит,
0sin
1
sinlim =
⋅
→∞
n
n
n
.
г) Имеем неопределенность типа
(
)
∞
1.
()
=
+=
+=
−
+
+=
+
+⋅⋅
∞→
+
∞→
+
∞→
+
∞→
13
9
9
13
13
13
9
1
1lim
9
1
1lim1
9
1lim
9
lim
n
n
n
n
n
n
n
n
n
n
nn
n
n
n
n
27
927
lim
927
9
9
9
1
1lim ee
n
n
n
n
n
n
n
n
n
==
∞→=
+=
+
∞→
+
∞→
.
3. а) =
−+++−
−++−
=
=
+−
+−
→→
)3)(1(
)2)(1(
lim
0
0
34
23
lim
234
23
1
5
4
1
xxxxx
xxxx
xx
xx
xx
1
3
2
lim
234
23
1
=
−++
+
−++
=
→
x
x
x
x
xxx
x
.
б)
(
)
()
=∞−∞=+−+
∞→
12lim
22
xxx
x
(
)
(
)
(
)
(
)
(
)
=
+++
−−+
=
+++
++++−+
=
∞→∞→
12
12
lim
12
1212
lim
22
22
22
2222
xxx
xxx
xxx
xxxxxx
xx
(
)
=
+++
−
=
∞→
12
12
lim
22
xxx
x
x
=
∞
∞
1
11
2
1
1
2
1
1
2
lim =
+
=
+++
−
∞→
xx
x
x
.
в)
{}
=
+
=
+
==−==
=
−
→→→→
t
e
t
t
e
et
text
ex
e
x
ttexex
1ln
lim
ln
lim0lim,
0
0
ln
lim
00
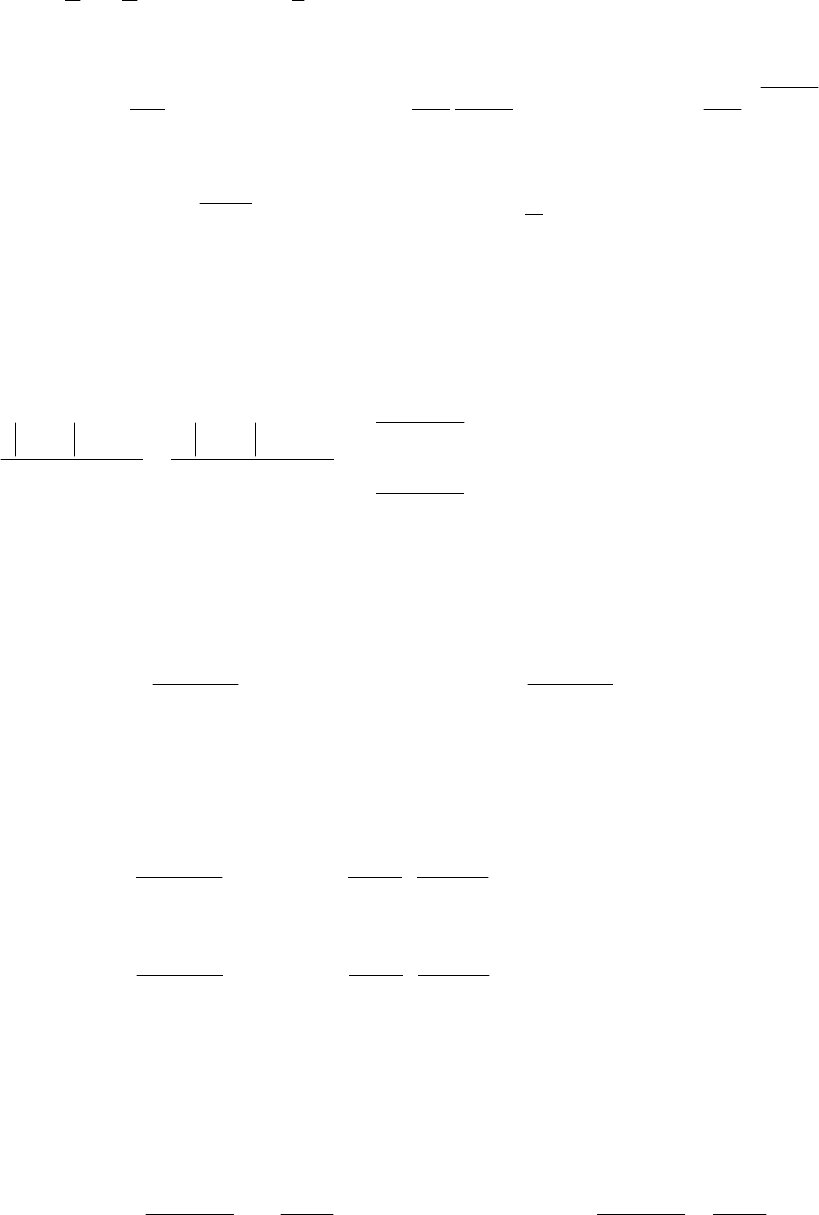
35
1lim0,~1ln
0
==
→
+=
→
t
t
t
e
t
e
t
t
.
г)
()
()
() ()
=
+=+==+
−
→
−
⋅
→
∞
−
→
x
x
x
x
x
x
x
x
x
x
xxx
7
sin10
sin
1
0
7
sin10
sin
1
0
7
10
0
sin1limsin1lim1sin1lim
{}
{}
7
10
7
sin10
0
lim
0
0,~sin0sinlim
−
−
→
→
=→==== exxxex
x
x
x
x
.
4.
()()()
(
)
+
∞∪∪−∪−∞−= ;22;00;11;)( fD .
1−=
x
, 0=
x
, 2=
x
– точки разрыва функции.
>
+
<
+
−
=
+−
−
=
−−
−
=
2,
)1(
sin
2,
)1(
sin
)1)(2(
sin2
2
sin2
23
x
xx
x
x
xx
x
xxx
xx
xxx
xx
y .
Вычислим односторонние пределы в точках разрыва.
1) 1−=
x
+∞=
+
−
=
−−→−−→
)1(
sin
limlim
0101
xx
x
y
xx
,
−∞=
+
−
=
−−→−−→
)1(
sin
limlim
0101
xx
x
y
xx
. Следователь-
но, 1−=
x
является точкой разрыва второго рода.
2) 0=
x
1
)1(
1sin
lim
)1(
sin
limlim
000000
−=
+
⋅−=
+
−
=
−→−→−→
xx
x
xx
x
y
xxx
,
1
)1(
1sin
lim
)1(
sin
limlim
000000
−=
+
⋅−=
+
−
=
+→+→+→
xx
x
xx
x
y
xxx
.
Односторонние пределы конечны и равны, следовательно, 0=
x
– точка
разрыва первого рода, точка устранимого разрыва.
3) 2=
x
6
2sin
)1(
sin
limlim
0202
−=
+
−
=
−→−→
xx
x
y
xx
,
6
2sin
)1(
sin
limlim
0202
=
+
=
+→+→
xx
x
y
xx
.
Односторонние пределы конечны, но не равны, следовательно, 2=
x
– точ-
ка разрыва первого рода, точка разрыва с конечным скачком.

36
5. а)
x
x
y
1
2
+
= .
);0()0;()( +∞∪−∞=
f
D . 0=
x
– точка разрыва.
−∞=
+
=
−→−→
x
x
y
xx
1
limlim
2
0000
; +∞=
+
=
+→+→
x
x
y
xx
1
limlim
2
0000
, следовательно,
0=
x
– уравнение вертикальной асимптоты.
Найдем наклонные асимптоты:
1
1
lim
)(
lim
2
2
=
+
==
∞−→∞−→
x
x
x
xf
k
xx
;
0
1
lim
1
lim))((lim
2
==
−
+
=−=
∞−→∞−→∞−→
x
x
x
x
kxxfb
xxx
.
Следовательно,
x
y
=
– наклонная асимптота при
−
∞→
x
.
Аналогично, находим, что
x
y = – наклонная асимптота при
+∞→
x
.
б)
arctgyx x=+ .
);()( +∞−∞=
f
D . Вертикальных асимптот нет. Найдем наклонные асимпто-
ты.
1)
1
arctg
1lim
)(
lim =
+==
−∞→−∞→
x
x
x
xf
k
xx
,
2
arctglim))((lim
π
−==−=
−∞→−∞→
xxxfb
xx
.
Следовательно,
2
π
−= xy – наклонная асимптота при −∞→
x
.
2)
1
arctg
1lim
)(
lim =
+==
+∞→+∞→
x
x
x
xf
k
xx
,
2
arctglim))((lim
π
==−=
+∞→+∞→
xxxfb
xx
.
Следовательно,
2
π
+= xy – наклонная асимптота при +∞→
x
.

37
6. Рассмотрим функцию xxxy
xx 222
2
sin12)1( +−⋅+=
++
, она непрерывна
на всей числовой прямой. Так как 04)0( >
=
y и 01sin2)1(
2
<−=−y , то по
теореме о существовании корня существует точка )0;1(
0
−
∈
x такая, что
0)(
0
=xy , тем самым доказано существование корня у исходного уравне-
ния.
Для нахождения приближенного значения корня
0
x применим метод поло-
винного деления. Чтобы найти приближенное значение корня с точностью
0,01, нужно найти отрезок длины, меньшей 0,01, в котором есть корень.
Взяв любую точку этого отрезка за приближенное значение корня, полу-
чим, что погрешность приближенного значения не превосходит длины от-
резка. Чтобы обеспечить требуемую точность, нужно осуществить не ме-
нее семи делений
≈>⇒<
−−
64,6100log01,0
2
)1(0
2
n
n
.
Из выше сказанного следует, что
)0;1(
0
−
∈
x .
1 шаг) поделим отрезок ]0;1[− пополам и найдем значение функции при
5,0−=
x
: 0425,1)5,0( >
≈
−
f
, следовательно, ]5,0;1[
0
−
−
∈
x .
2 шаг) поделим пополам отрезок
]5,0;1[
−
−
и найдем значение функции при
75,0−=
x
: 0297,0)75,0( >≈−
f
, следовательно,
]75,0;1[
0
−
−
∈
x
.
3шаг) 0319,0)875,0( <
−
≈−
f
⇒ ]75,0;875,0[
0
−
−
∈
x ;
4 шаг) 00043,0)8125,0( <−
≈
−
f
⇒ ]75,0;8125,0[
0
−
−
∈
x ;
5 шаг)0148,0)78125,0( >≈−
f
⇒ ]78125,0;8125,0[
0
−
−
∈
x ;
6 шаг)0072,0)796875,0( >≈−
f
⇒ ]796875,0;8125,0[
0
−
−
∈
x ;
7 шаг)0034,0)8046875,0( >≈−
f
⇒ ]8046875,0;8125,0[
0
−
−
∈
x
.
Теперь за приближенное значение корня можем взять любое число из от-
резка
]8046875,0;8125,0[ −−
. Возьмем за приближенное значение корня се-
редину отрезка, то есть
81,080859375,0
0
−
≈
−≈x
.
38
Контрольная работа № 2
В настоящей работе представлены варианты контрольной работы по
математическому анализу по теме «Дифференциальное исчисление
функции одной переменной».
Для выполнения первого задания требуется знать определение про-
изводной.
Второе задание посвящено дифференцированию функции. Для вы-
полнения этого задания необходимо знание и применение: дифференциро-
вания элементарных функций; правил вычисления производной суммы,
произведения, частного. Кроме того, требуется повторить правила диффе-
ренцирования сложной функции и нахождения логарифмической произ-
водной.
В третьем задании требуется применить правило Лопиталя для вы-
числения предела отношения двух функций.
В качестве четвертого задания предлагается вычислить производную
функции, заданной неявно. Для этого следует вспомнить понятие диффе-
ренциала функции и правила дифференцирования.
В пятом задании требуется вычислить приближенное значение
функции в точке с помощью дифференциала.
Последующие три задания посвящены приложению производных к
экономике и финансам.
Содержание шестого задание составляет нахождение эластичности
функции спроса в точке рыночного равновесия. Для выполнения этого за-
дания надо найти точку рыночного равновесия, а затем применить форму-
лу для эластичности функции в точке.
В седьмом задании требуется оценить с помощью дифференциала
изменение равновесной цены при введении дополнительного налога. Для
39
успешного решения поставленной задачи следует сначала найти равновес-
ную цену, а после этого применить формулу для приращения цены.
Восьмое задание посвящено нахождению момента времени, в кото-
рый выгоднее всего продать актив. Для решения этого задания рекоменду-
ется вспомнить, что мгновенная доходность актива совпадает с темпом
роста его стоимости, а затем вычислить интервал времени, в который вы-
годнее всего купить или продать актив.
Необходимые понятия, определения и теоремы можно найти в реко-
мендованных пособиях [1], [2], [3], [5].
